Похожие презентации:
Теория систем и системный анализ Сетевое планирование (расчет сетевого графика)
1.
Теория системи
системный анализ
Сетевое планирование
(расчет сетевого графика)
2.
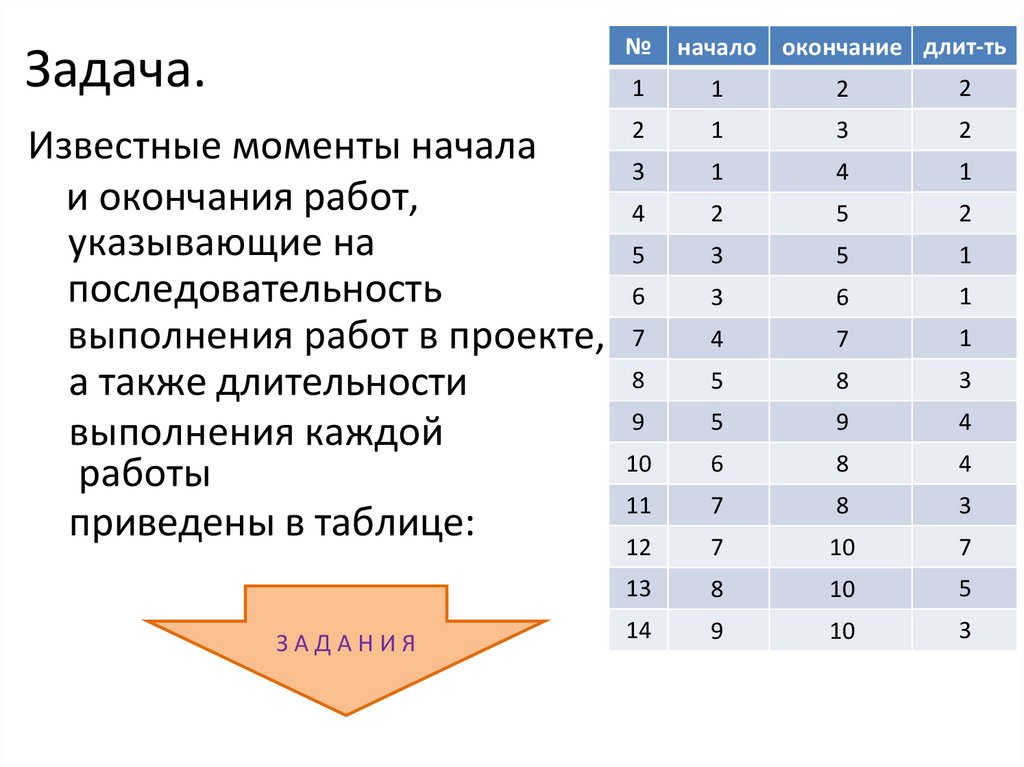
№ начало окончание длит-тьЗадача.
1
1
2
2
2
Известные моменты начала
3
и окончания работ,
4
указывающие на
5
последовательность
6
выполнения работ в проекте, 7
8
а также длительности
9
выполнения каждой
10
работы
11
приведены в таблице:
12
1
3
2
1
4
1
2
5
2
3
5
1
3
6
1
4
7
1
5
8
3
5
9
4
6
8
4
7
8
3
7
10
7
13
8
10
5
14
9
10
3
ЗАДАНИЯ
3.
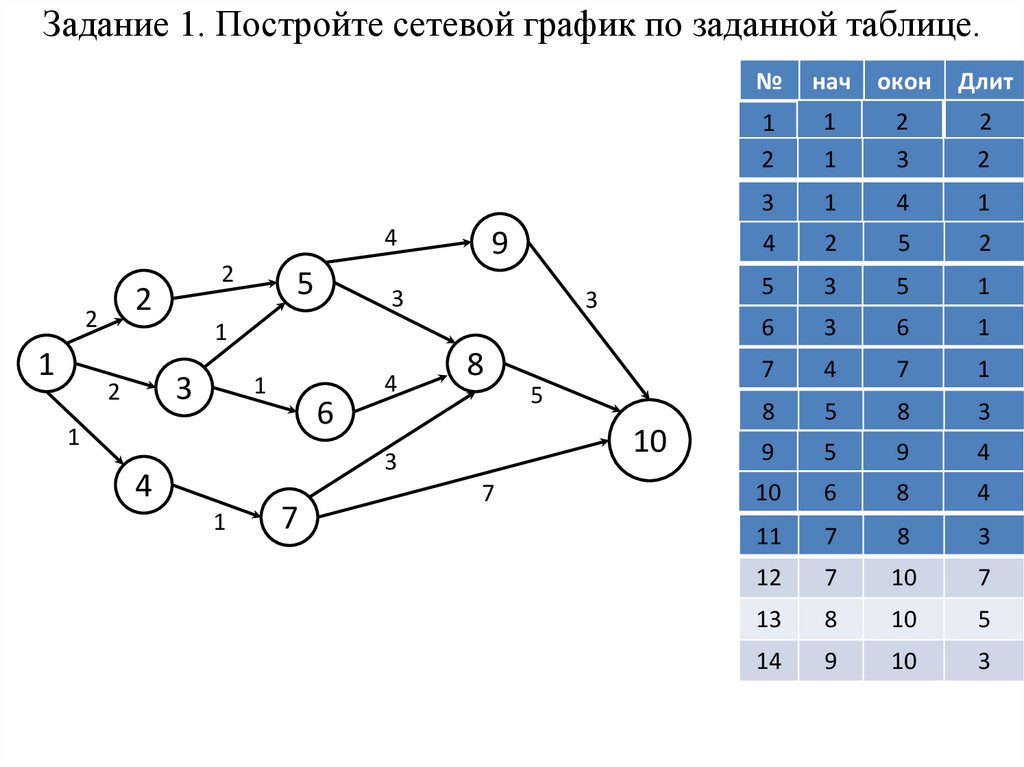
Задание 1. Постройте сетевой график по заданной таблице.4
2
2
1
2
5
9
3
3
1
3
2
1
6
1
4
8
5
10
3
4
1
7
7
№
нач
окон
Длит
1
2
1
1
2
3
2
2
3
1
4
1
4
2
5
2
5
3
5
1
6
3
6
1
7
4
7
1
8
5
8
3
9
5
9
4
10
6
8
4
11
7
8
3
12
7
10
7
13
8
10
5
14
9
10
3
4.
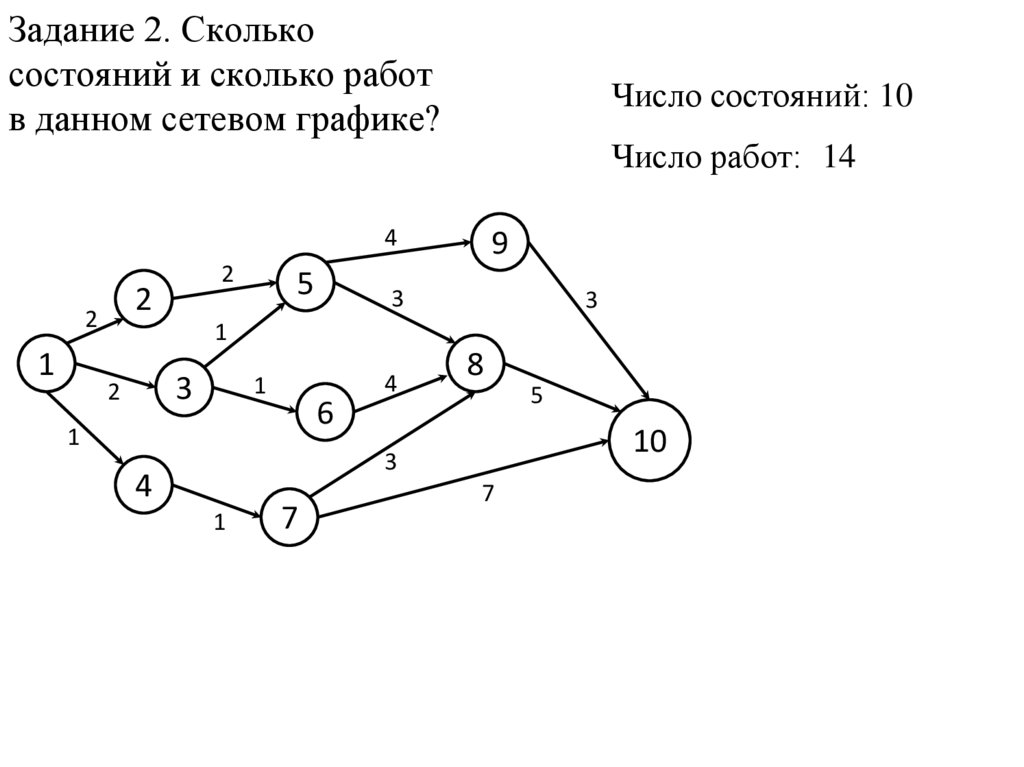
Задание 2. Сколькосостояний и сколько работ
в данном сетевом графике?
Число состояний: 10
Число работ: 14
4
2
2
1
2
5
9
3
3
1
3
2
1
6
1
4
8
5
10
3
4
1
7
7
5.
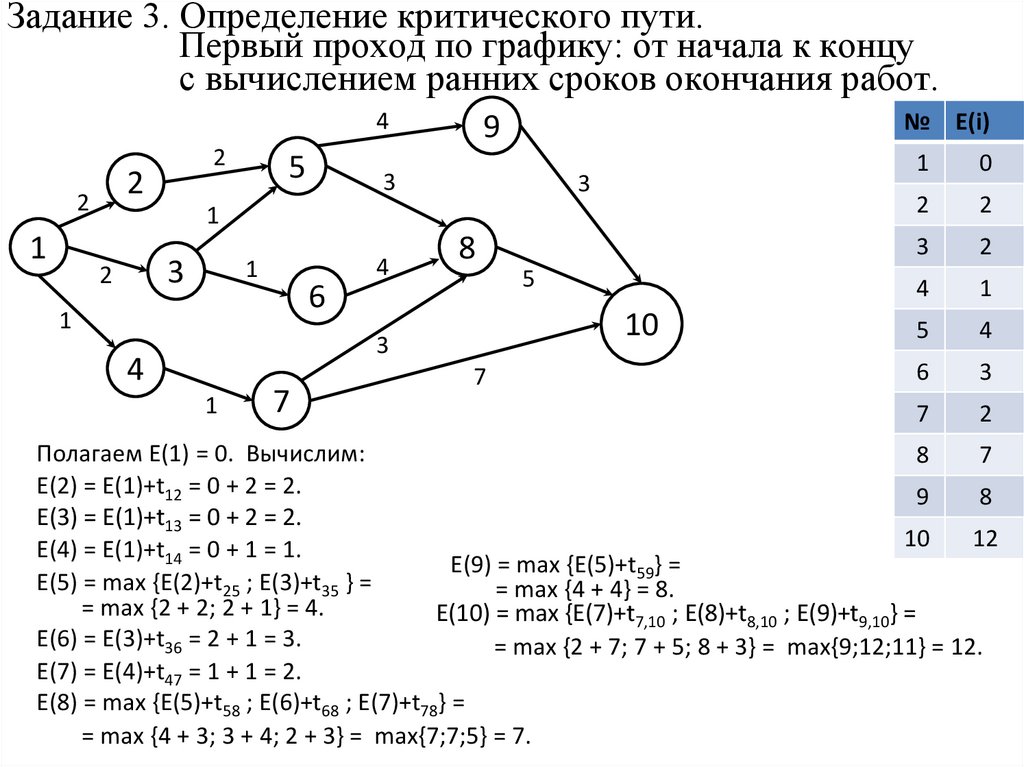
Задание 3. Определение критического пути.Первый проход по графику: от начала к концу
с вычислением ранних сроков окончания работ.
4
2
2
1
2
5
№ E(i)
9
3
3
1
3
2
1
6
1
4
8
5
10
3
4
1
7
7
1
0
2
2
3
2
4
1
5
4
6
3
7
2
Полагаем E(1) = 0. Вычислим:
8
7
E(2) = E(1)+t12 = 0 + 2 = 2.
9
8
E(3) = E(1)+t13 = 0 + 2 = 2.
10
12
E(4) = E(1)+t14 = 0 + 1 = 1.
E(9) = max {E(5)+t59} =
E(5) = max {E(2)+t25 ; E(3)+t35 } =
= max {4 + 4} = 8.
= max {2 + 2; 2 + 1} = 4.
E(10) = max {E(7)+t7,10 ; E(8)+t8,10 ; E(9)+t9,10} =
E(6) = E(3)+t36 = 2 + 1 = 3.
= max {2 + 7; 7 + 5; 8 + 3} = max{9;12;11} = 12.
E(7) = E(4)+t47 = 1 + 1 = 2.
E(8) = max {E(5)+t58 ; E(6)+t68 ; E(7)+t78} =
= max {4 + 3; 3 + 4; 2 + 3} = max{7;7;5} = 7.
6.
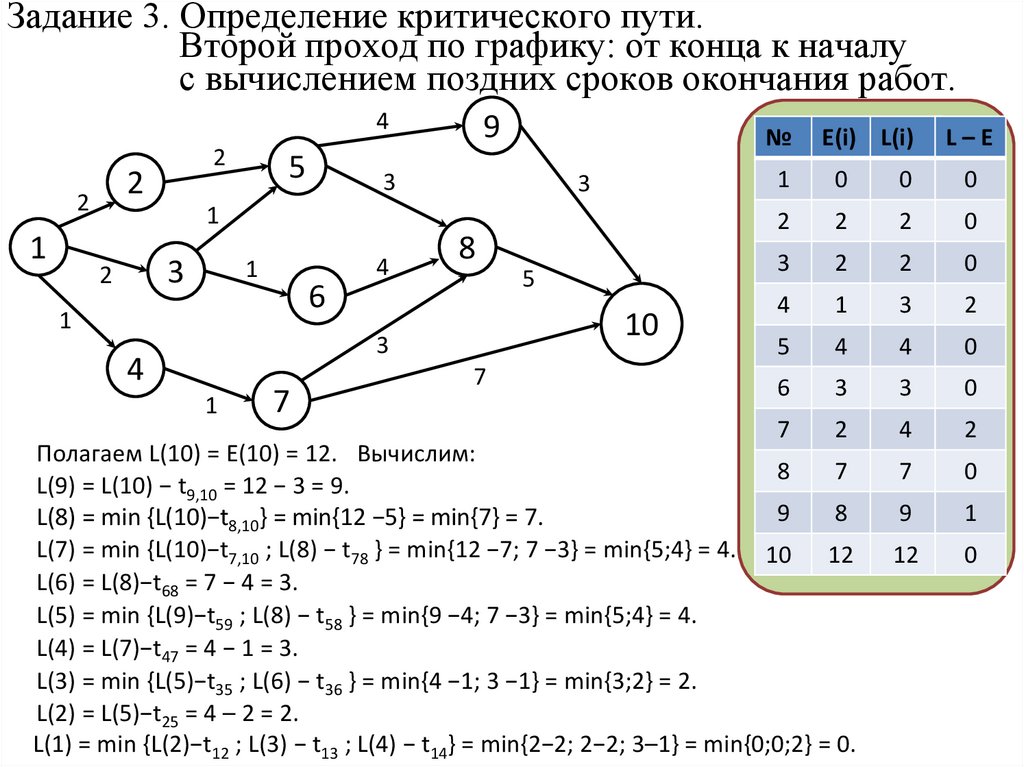
Задание 3. Определение критического пути.Второй проход по графику: от конца к началу
с вычислением поздних сроков окончания работ.
4
2
2
1
2
5
9
3
3
1
3
2
1
6
1
4
8
5
10
3
4
1
7
7
№
E(i) L(i)
1
0
0
0
2
2
2
0
3
2
2
0
4
1
3
2
5
4
4
0
6
3
3
0
7
2
4
2
7
0
9
1
12
0
Полагаем L(10) = E(10) = 12. Вычислим:
8
7
L(9) = L(10) − t9,10 = 12 − 3 = 9.
9
8
L(8) = min {L(10)−t8,10} = min{12 −5} = min{7} = 7.
L(7) = min {L(10)−t7,10 ; L(8) − t78 } = min{12 −7; 7 −3} = min{5;4} = 4. 10 12
L(6) = L(8)−t68 = 7 − 4 = 3.
L(5) = min {L(9)−t59 ; L(8) − t58 } = min{9 −4; 7 −3} = min{5;4} = 4.
L(4) = L(7)−t47 = 4 − 1 = 3.
L(3) = min {L(5)−t35 ; L(6) − t36 } = min{4 −1; 3 −1} = min{3;2} = 2.
L(2) = L(5)−t25 = 4 – 2 = 2.
L(1) = min {L(2)−t12 ; L(3) − t13 ; L(4) − t14} = min{2−2; 2−2; 3–1} = min{0;0;2} = 0.
L–E
7.
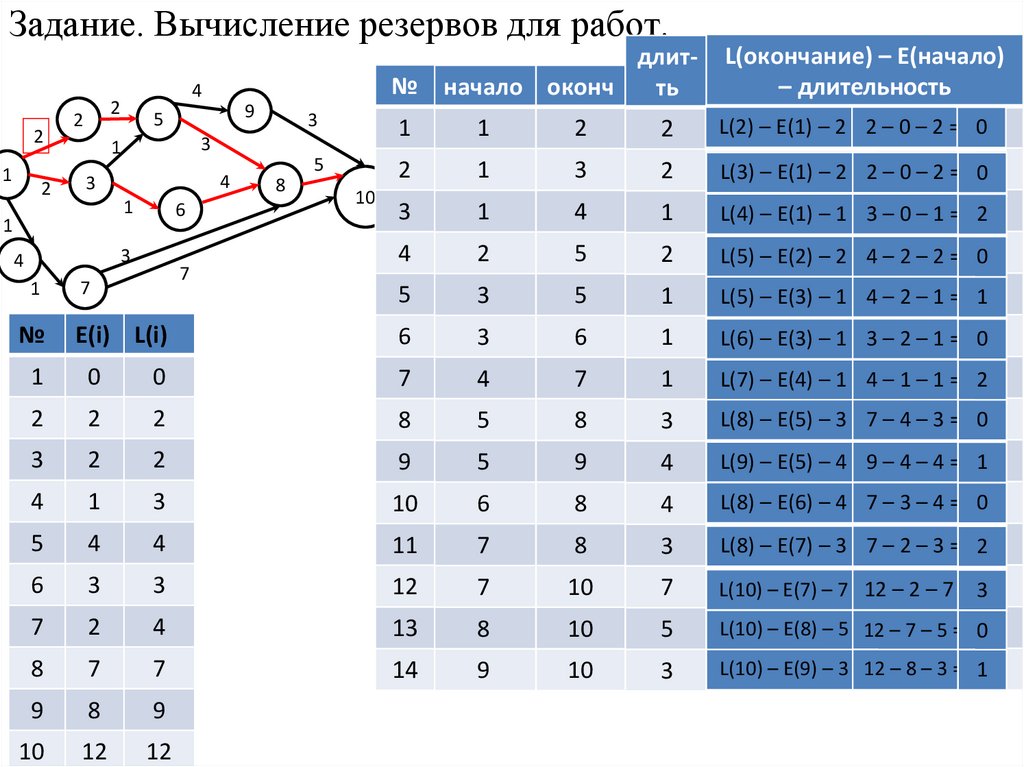
Задание. Вычисление резервов для работ.2
1
2
9
5
4
3
1
6
3
4
3
1
1
2
2
L(2) – E(1) – 2 = 2 – 0 – 2 = 0
5
2
1
3
2
L(3) – E(1) – 2 = 2 – 0 – 2 = 0
3
1
4
1
L(4) – E(1) – 1 = 3 – 0 – 1 = 2
4
2
5
2
L(5) – E(2) – 2 = 4 – 2 – 2 = 0
5
3
5
1
L(5) – E(3) – 1 = 4 – 2 – 1 = 1
3
1
1
L(окончание) – E(начало)
– длительность
4
2
2
длит№ начало оконч
ть
7
8
10
1
7
№
E(i) L(i)
6
3
6
1
L(6) – E(3) – 1 = 3 – 2 – 1 = 0
1
0
0
7
4
7
1
L(7) – E(4) – 1 = 4 – 1 – 1 = 2
2
2
2
8
5
8
3
L(8) – E(5) – 3 = 7 – 4 – 3 = 0
3
2
2
9
5
9
4
L(9) – E(5) – 4 = 9 – 4 – 4 = 1
4
1
3
10
6
8
4
L(8) – E(6) – 4 = 7 – 3 – 4 = 0
5
4
4
11
7
8
3
L(8) – E(7) – 3 = 7 – 2 – 3 = 2
6
3
3
12
7
10
7
L(10) – E(7) – 7 =12 – 2 – 7 = 3
7
2
4
13
8
10
5
L(10) – E(8) – 5 =12 – 7 – 5 = 0
8
7
7
14
9
10
3
L(10) – E(9) – 3 =12 – 8 – 3 = 1
9
8
9
10
12
12
8.
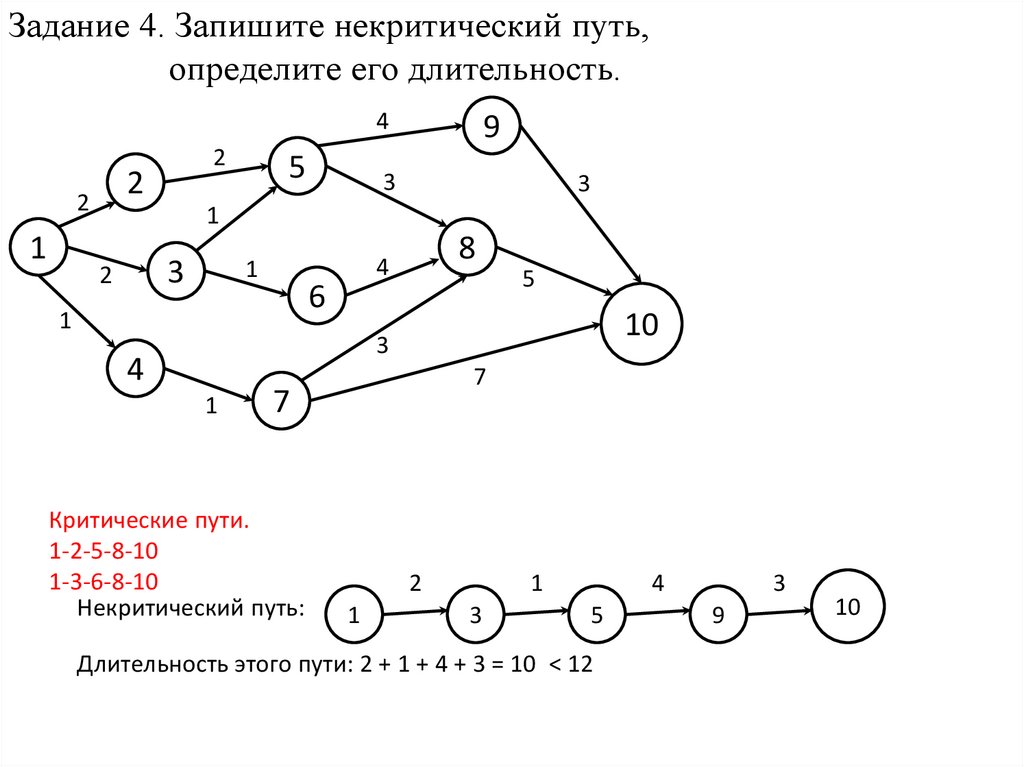
Задание 4. Запишите некритический путь,определите его длительность.
4
2
2
1
2
5
9
3
3
1
3
2
1
6
1
8
4
5
10
3
4
1
7
7
Критические пути.
1-2-5-8-10
1-3-6-8-10
Некритический путь:
2
1
1
3
4
5
Длительность этого пути: 2 + 1 + 4 + 3 = 10 < 12
3
9
10


 Информатика
Информатика








