Урок 10ВИС

1.

Операции над множествами:
объединение, пересечение,
дополнение.

2.

Объединение множеств
Определение. Объединение множества А и множества В называется множество A ∪ B,
которое состоит из всех элементов исходных множеств A и B вместе. То есть в
объединение попадут вообще все элементы, которые были хотя бы в одном из
исходных множеств.
Заметим, что при объединении множеств общие элементы множеств не повторяются.
Пример 1.
Найдём попарные объединения множеств из опыта с кубиком:
А = «выпадет чётное число очков» = {2, 4, 6};
B = «выпадет шестёрка» = {6};
C = «выпадет простое число» = {2, 3, 5}.
Получаем: A B = {2, 4, 6},
A C = {2, 3, 4, 5, 6},
B C = {2, 3, 5, 6}

3.

ПРИМЕР 2.
A = {100, 200, 300, 400, 500}
B = {100, 500, 1000, 1500}
A ∪ B = {100, 200, 300, 400, 500, 1000, 1500}.
ПРИМЕР 3.
А) Если B — множество книг по здоровому питанию и A — множество
статей по здоровому питанию, то B ∪ A — множество книг и статей
по здоровому питанию.
Б) Если O — множество апельсинов и M — мандаринов, то O ∪ M —
общее множество апельсинов и мандаринов вместе.
С) Если F — множество уроков с первого по пятый и L — множество
уроков с третьего по шестой, то F ∪ L — множество уроков с первого
по шестой.

4.

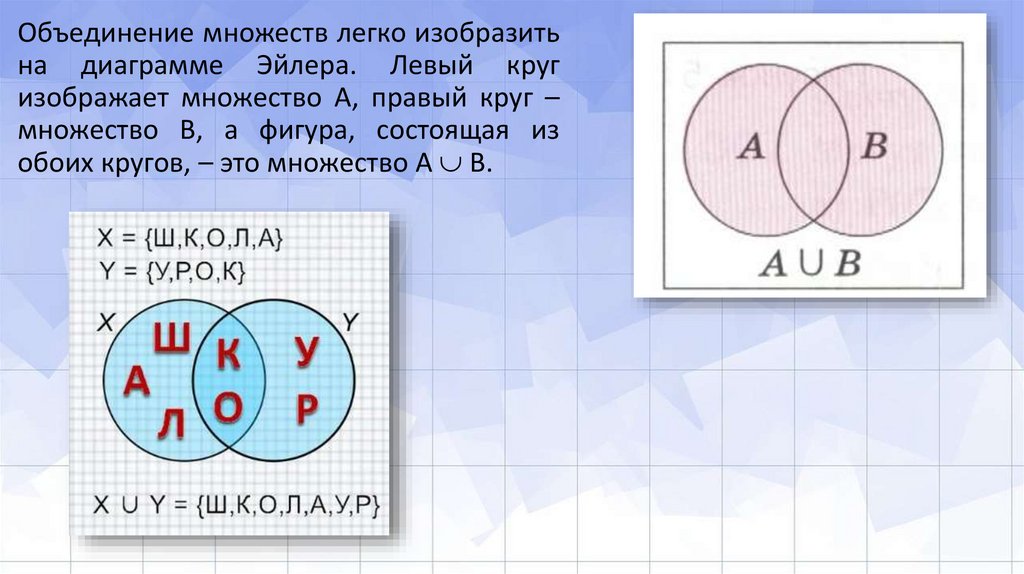
Объединение множеств легко изобразить
на диаграмме Эйлера. Левый круг
изображает множество А, правый круг –
множество В, а фигура, состоящая из
обоих кругов, – это множество A B.

5.

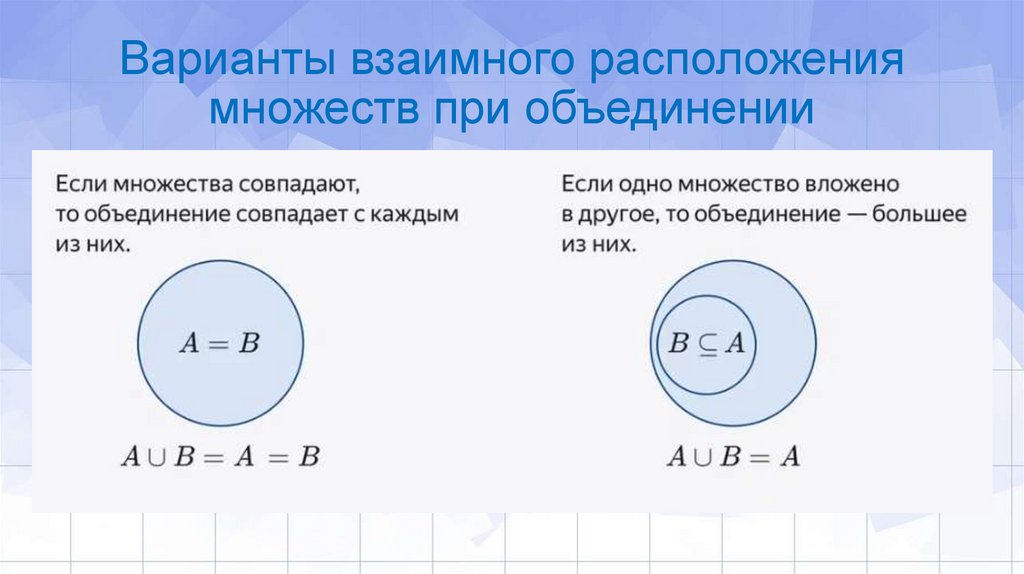
Варианты взаимного расположения
множеств при объединении

6.

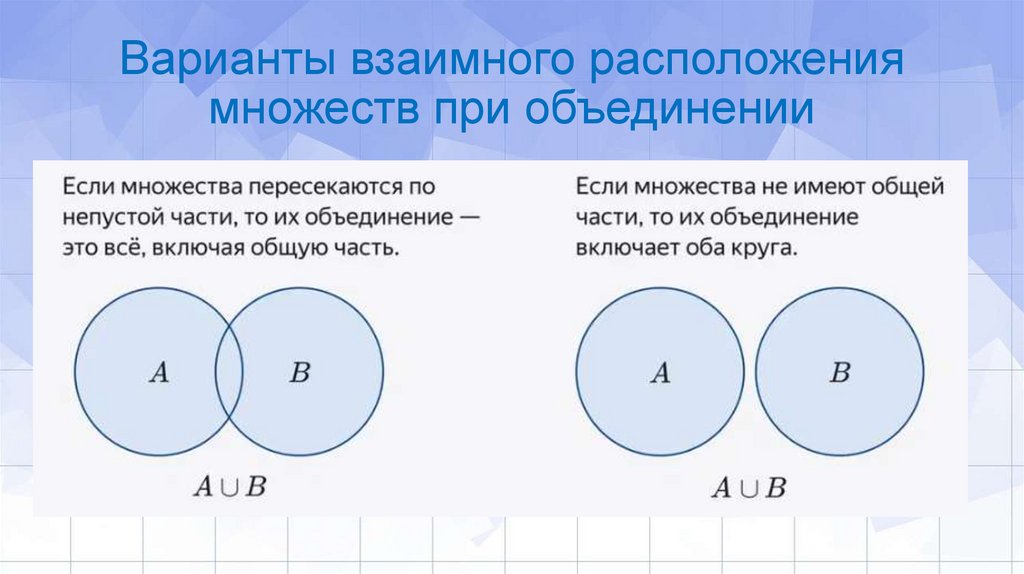
Варианты взаимного расположения
множеств при объединении

7.

Пересечений событий
Определение. Пересечение A ∩ B двух множеств A и B состоит из
элементов, которые принадлежат обоим исходным множествам.
Пример 4. Вернёмся к примеру с кубиком и найдём попарные пересечения
множеств:
А = «выпадет чётное число очков» = {2, 4, 6};
B = «выпадет шестёрка» = {6};
C = «выпадет простое число» = {2, 3, 5}.
A B = {6},
A C = {2},
B C = .

8.

ПРИМЕР 5.
A = {100, 200, 300, 400, 500}
B = {100, 500, 1000, 1500}
A B = {100, 500}.
ПРИМЕР 6.
А) Если H — множество упражнений, укрепляющих руки, и L —
множество упражнений, укрепляющих ноги, то H ∩ L — множество
упражнений, укрепляющих руки и ноги.
Б) Если A — множество яблок и G — множество зелёных предметов,
то A ∩ G — множество зелёных яблок.
В) Если E — множество песен на английском языке и J — множество
песен Дженнифер Лопес, то E ∩ J — множество песен Дженнифер
Лопес на английском языке.

9.

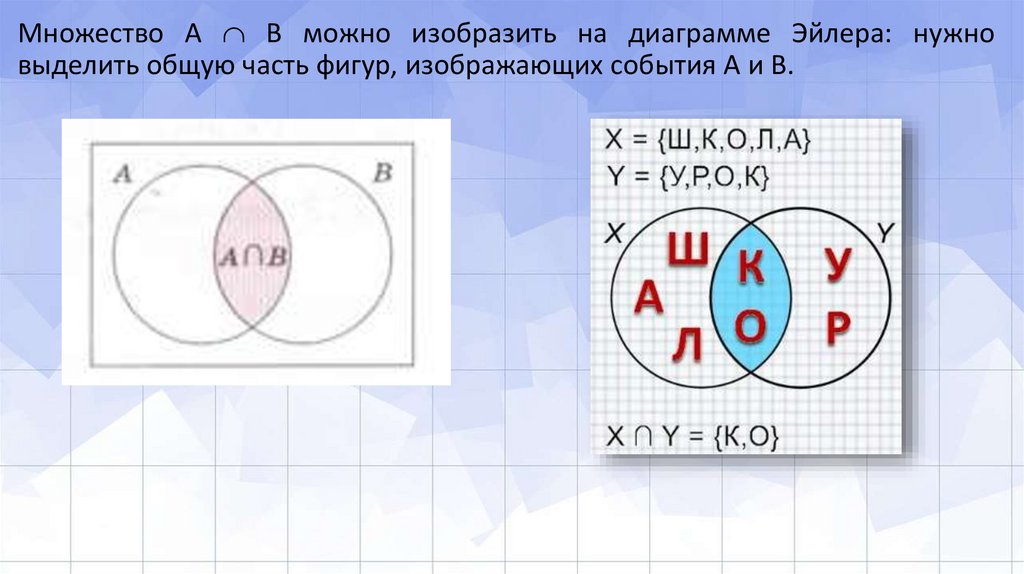
Множество А В можно изобразить на диаграмме Эйлера: нужно
выделить общую часть фигур, изображающих события А и В.

10.

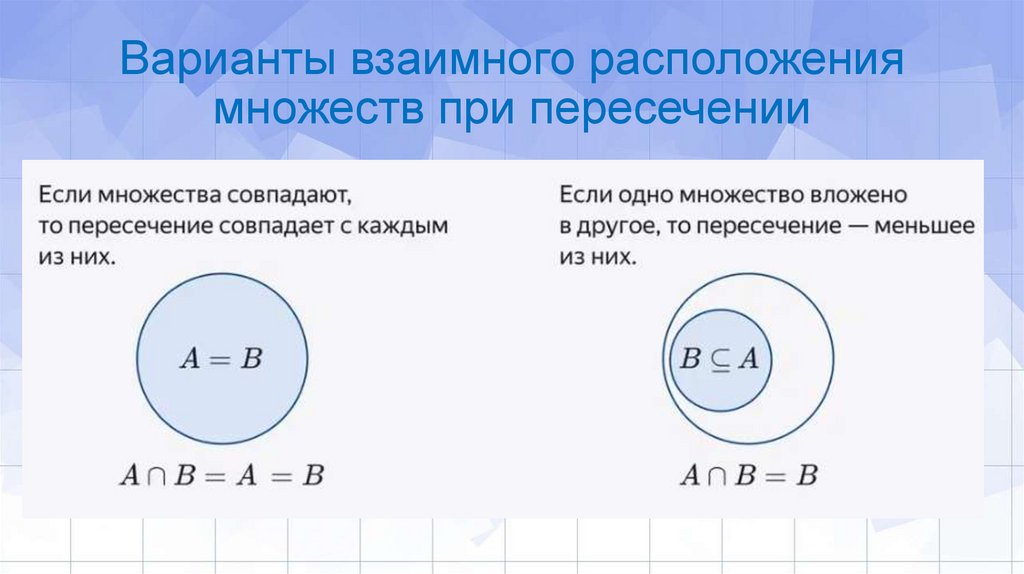
Варианты взаимного расположения
множеств при пересечении

11.

Варианты взаимного расположения
множеств при пересечении

12.

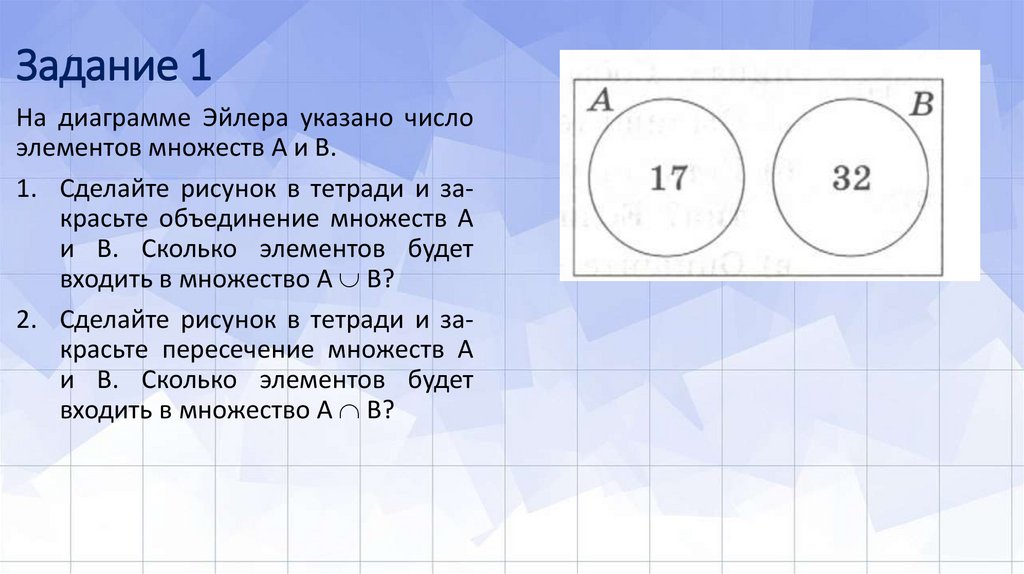
Пример 7
Найдём пересечения событий, связанных с футбольным матчем:
А = «матч закончится вничью»;
В = «Динамо» не забьёт ни одного гола»;
С = «Спартак» выиграет».
Снова воспользуемся логикой. Пересечению множеств, как вы помните,
соответствует логическая операция «и», которой мы и воспользуемся:
A B = «матч закончится вничью, и «Динамо» не забьёт ни одного гола» =
«матч закончится со счётом 0 : 0»;
A C = ;
B C = «Спартак» забьёт хотя бы один гол».
Заметим, что при нахождении B C мы использовали тот факт, что
событие B произошло (команда «Динамо» не забила ни одного гола), а
значит, «Спартаку» для победы достаточно забить хотя бы один гол.

13.

Дополнением к множеству A называется множество