Похожие презентации:
Парабола. Уравнение директрисы параболы
1.
ПАРАБОЛОЙ называется множествоточек плоскости, каждая из которых
находится на одинаковом расстоянии от
данной точки, называемой фокусом
параболы и данной прямой,
называемой директрисой.
2.
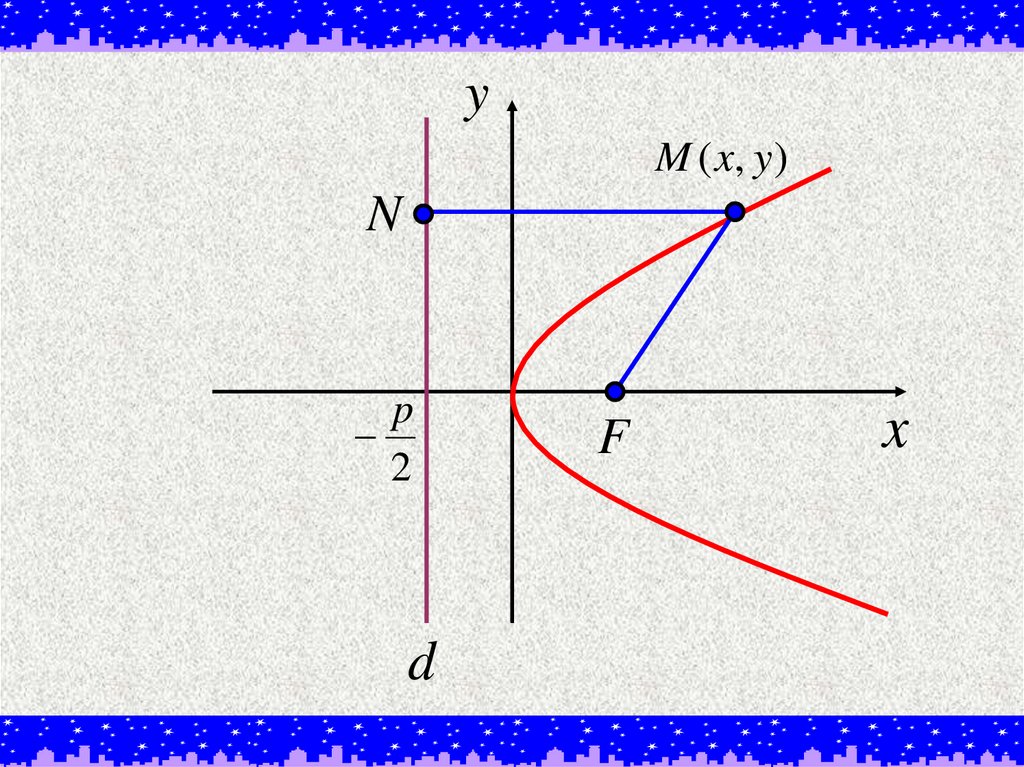
yM ( x, y )
N
p
2
d
F
x
3.
Введем обозначения:p
F ;0
2
Расстояние между фокусом
параболы равно р.
и
директрисой
Для любой точки М(х,у), принадлежащей
параболе, по определению выполняется
равенство:
FM NM
4.
Для того, чтобы точка М(х,у)принадлежала параболе, необходимо и
достаточно, чтобы ее координаты
удовлетворяли уравнению
y 2 px
2
5.
Покажем, что координаты точки, принадлежащейпараболе, удовлетворяют уравнению.
Т.к. точка М(х,у) принадлежит параболе, то по
определению параболы, должно выполнятся
условие
FM NM
Выразим каждое расстояние по
расстояния между двумя точками:
p
F ;0
2
M ( x; y)
формуле
2
p
2
FM x y
2
6.
pNM x
2
2
p
p
2
x y x
2
2
Тогда:
Возводим в квадрат обе части выражения:
2
p
p
2
2
x y x xp
4
2
2
2
2
p
p
2
2
x xp y x xp
4
4
2
7.
y 2 px2
8.
Уравнение директрисы параболы имеет вид:p
x
2
Расстояние
FM
называется фокальным радиусом точки М, р
называется параметром параболы.
В зависимости от значения этих параметров,
возможны различные способы ориентации
параболы на плоскости.
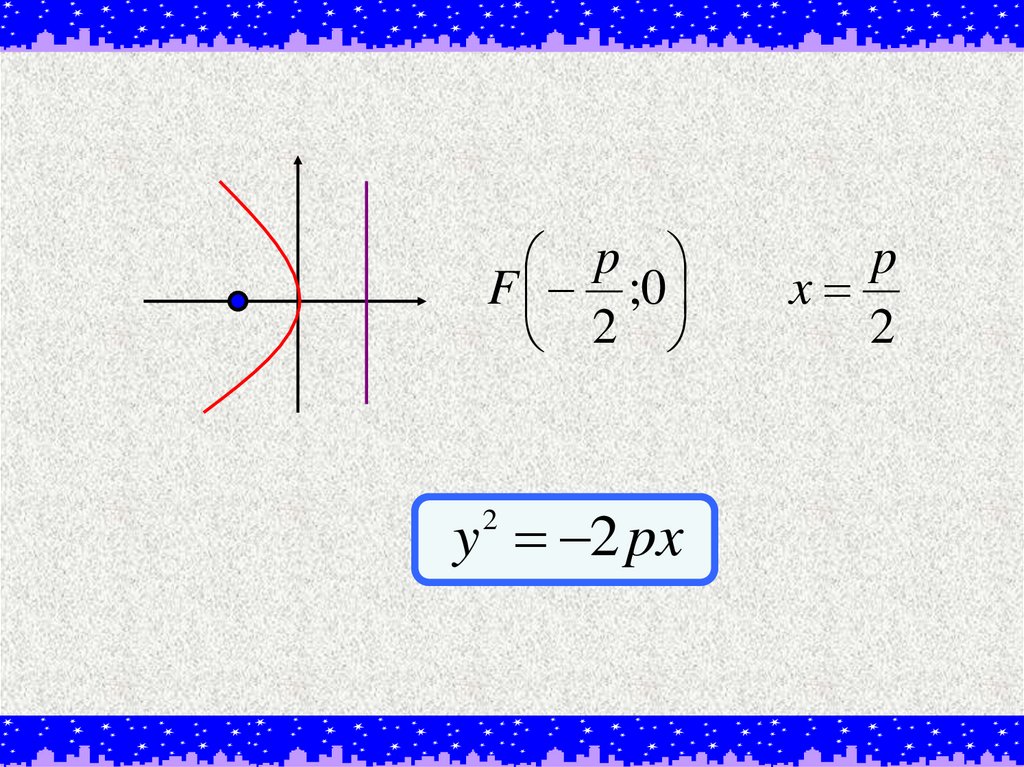
9.
pF ;0
2
y 2 px
2
p
x
2
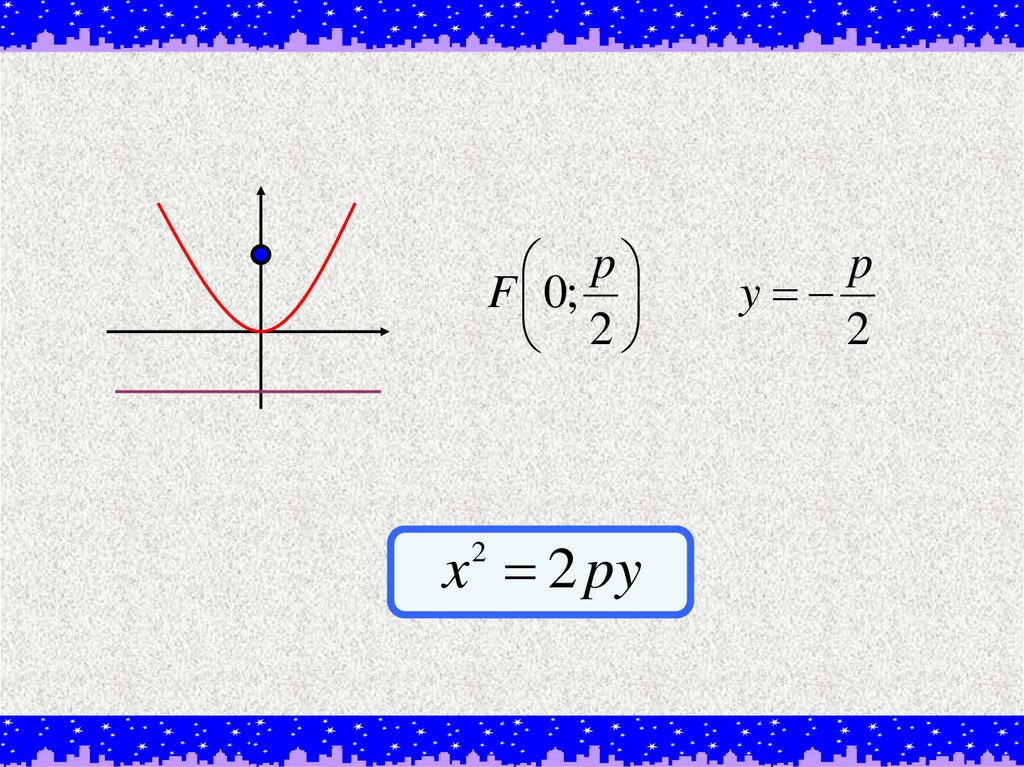
10.
pF 0;
2
x 2 py
2
p
y
2
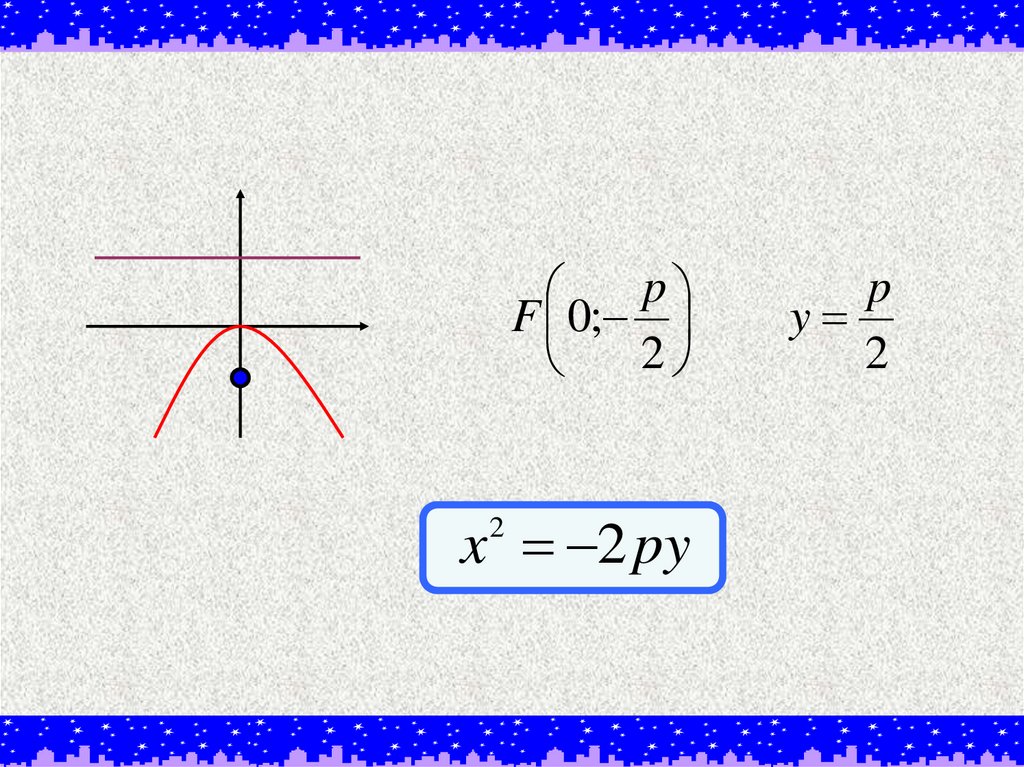
11.
pF 0;
2
x 2 py
2
p
y
2







 Математика
Математика








