Похожие презентации:
Функции нескольких переменных. Лекции
1.
Московский государственныймедико-стоматологический университет им. А.И.
Евдокимова
Функции
нескольких
Название
переменных
лекции
• ЭФ МАТЕМАТИКА
2.
Производная по направлению.Градиент и его свойства. Применение
функций многих переменных в
экономике
3.
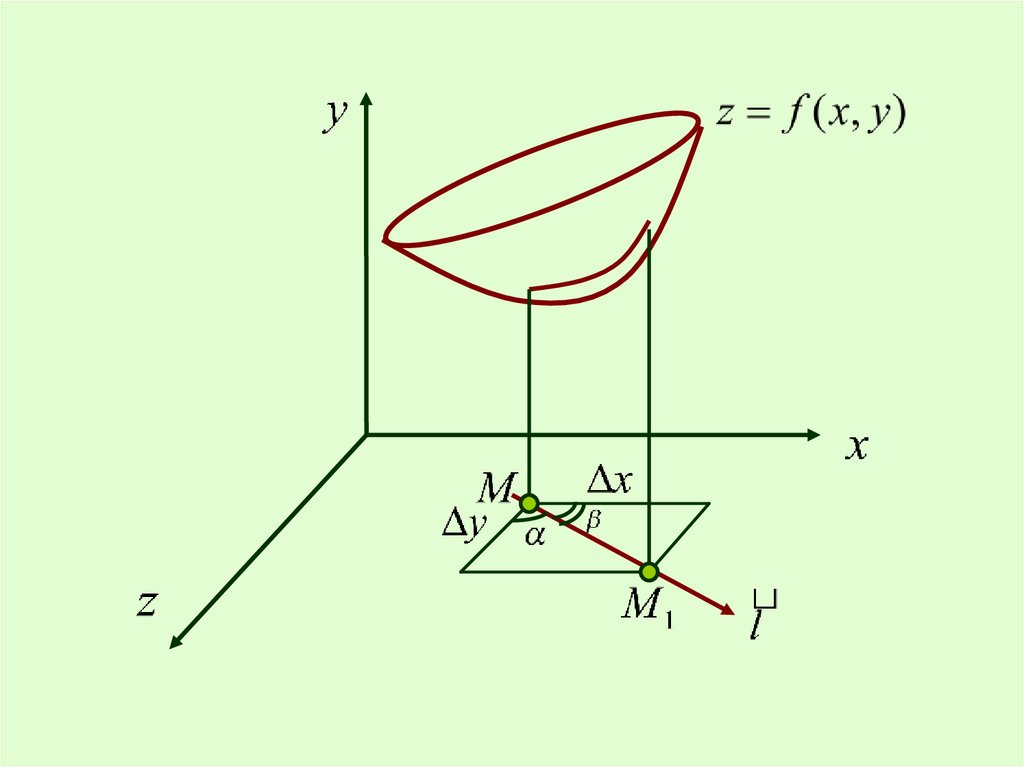
Пусть функция z=f(x,y) определена в некоторойокрестности точки М(х,у).
l – некоторое направление, задаваемое единичным
вектором
где
т.к.
4.
cosα, cosβ – косинусы углов, образованных даннымвектором с осями координат. Они называются
направляющими косинусами.
При перемещении в направлении l точки М(х,у) в
точку
Функция z получит приращение
которое называется приращением функции
данном направлении l.
z в
5.
Еслито
6.
7.
Производной по направлениюфункции двух переменных z=f(x,y)
называется предел отношения
приращения функции в этом
направлении к величине перемещения
Δl при
8.
Производная по направлению характеризуетскорость изменения функции в направлении l.
Рассмотренные ранее производные
есть производные по направлениям, параллельным
осям абсцисс и ординат, соответственно.
Покажем, что
9.
Делим обе части на Δl и переходим к пределу:10.
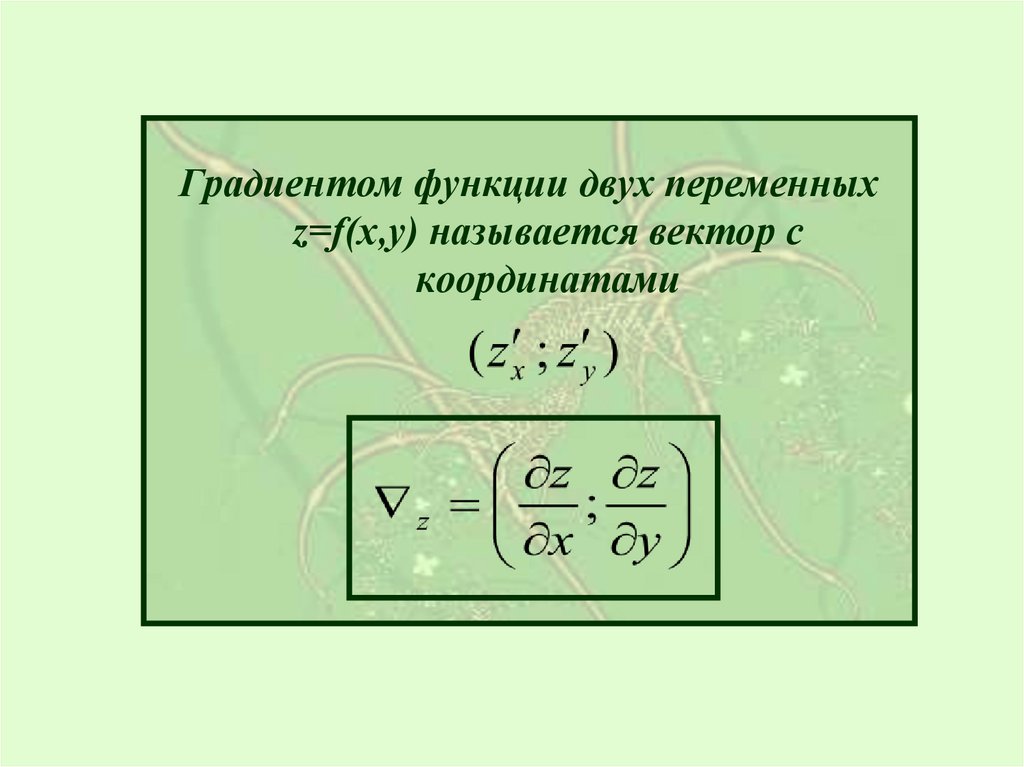
Градиентом функции двух переменныхz=f(x,y) называется вектор с
координатами
11.
Рассмотрим скалярное произведениеСкалярное произведение в координатах имеет
вид:
Поскольку
12.
Тогда13.
Производная по направлению есть скалярноепроизведение градиента и единичного
вектора, задающего данное направление.
Поскольку скалярное произведение максимально,
если вектора одинаково направлены, то
Градиент функции в данной точке
характеризует направление максимальной
скорости изменения функции в данной
точке.
14.
Если задана функция трех переменных f(x,y,z), тоградиент будет являться трехмерным вектором
с компонентами:
Или
15.
Пусть задана дифференцируемаяфункция z=f(x,y) и пусть в точке
М(х0,у0) величина градиента
отлична от нуля. Тогда градиент
перпендикулярен линии уровня,
проходящей через данную точку.
16.
Применение функций в экономикеФункции находят широкое применение в экономической
теории.
Спектр используемых функций весьма широк от
простейших линейных
до рекуррентных соотношений,
связывающих состояния различных объектов в разные
периоды времени.
Наиболее часто в экономике используются следующие
функции:
17.
1. Функция полезности (функция предпочтений) – в широкомсмысле полезности, т.е. результата, эффекта некоторого действия
от уровня (интенсивности) этого действия.
2. Производственная функция – зависимость результата
производственной деятельности от обусловивших его факторов.
3. Функция выпуска (частный вид производственной функции)
– зависимость объема производства от наличия или потребления
ресурсов.
18.
4. Функция издержек (частный вид производственнойфункции) – зависимость издержек производства от объема
продукции.
5. Функции спроса, потребления и предложения –
зависимость объема спроса, потребления или предложения
на отдельные товары или услуги от различных факторов.
Экономические явления и процессы обусловливаются
действием различных факторов, следовательно, для
исследования таких процессов используют функции
нескольких переменных.
19.
Например:- мультипликативные функции позволяют представить
зависимую переменную в виде произведения факторных
переменных;
- сепарабельные функции позволяют выделить влияние
различных
факторных
переменных
на
зависимую
переменную.
Одним из методов определения функциональных
зависимостей в экономике является анализ статистических
данных и экономических явлений в производственной и
непроизводственной сфере.
20.
Задача. Если известны постоянные издержки F (независящие от числа единиц произведенной продукции),
переменные издержки V (пропорциональные объему
продукции х) за каждую единицу продукции и цена единицы
продукции R, то объем продукции х при котором прибыль
равна
нулю
(точка
безубыточности)
определяется
следующим образом:
1. Составляется функция издержек производства
С ( x) F V x
2. Совокупный доход (выручка от реализации) продукции
K ( x) R x
3. Составляется функция прибыли
P( x) K ( x) C ( x) R x C ( x)
21.
4. Точка безубыточности – прибыль равна нулюP( x) R x C ( x) 0
Следовательно объем производства равен
C ( x)
x
R
Если известна (или задана) прибыль предприятия – S,
P( x) R x C ( x) S
то объем производства при известной или заданной
прибыли равен
S C ( x)
x
R
22.
Задача. Затраты на производство продукции выражаютсяуравнением y k x b где х – число месяцев.
1
1
Доход от реализации продукции выражается уравнением.
y k2 x b2
Определить начиная с какого времени производство будет
рентабельным.
Решение.
Производство считается рентабельным если затраты
равны доходу.
y k1 x b1
y k2 x b2







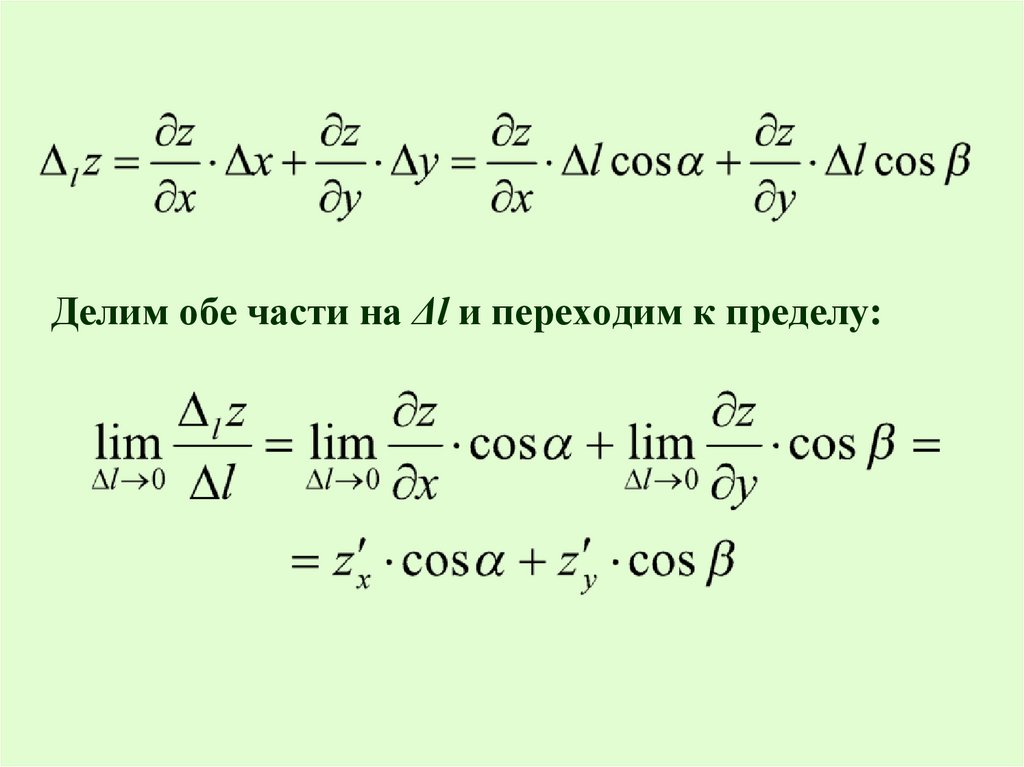
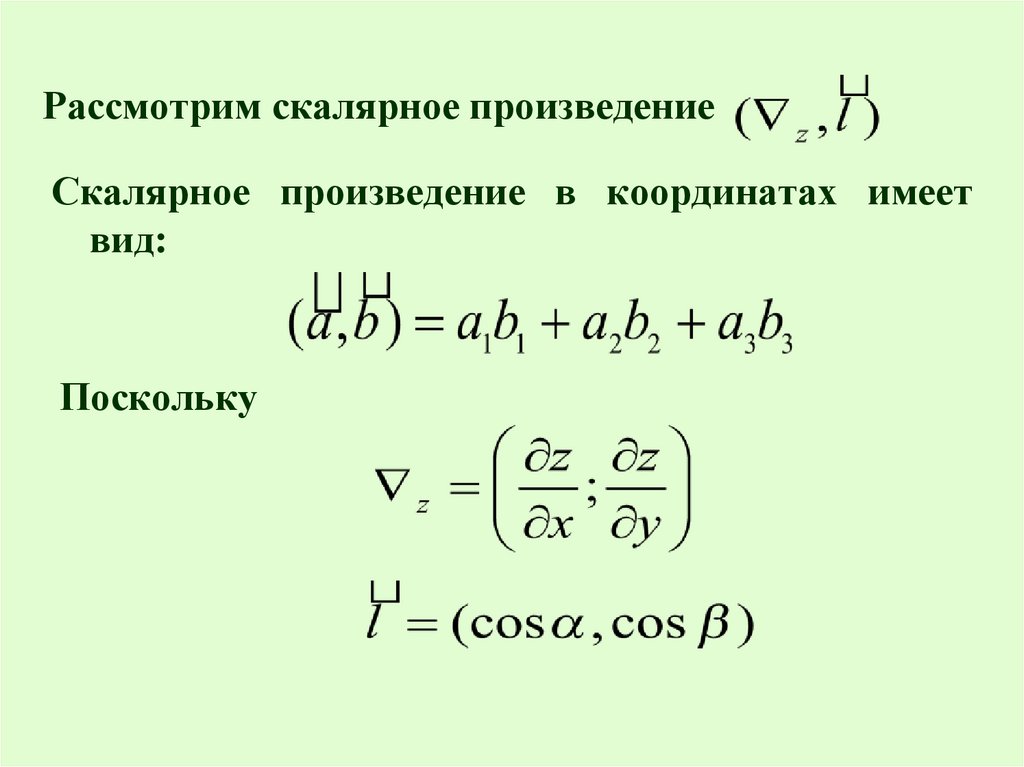
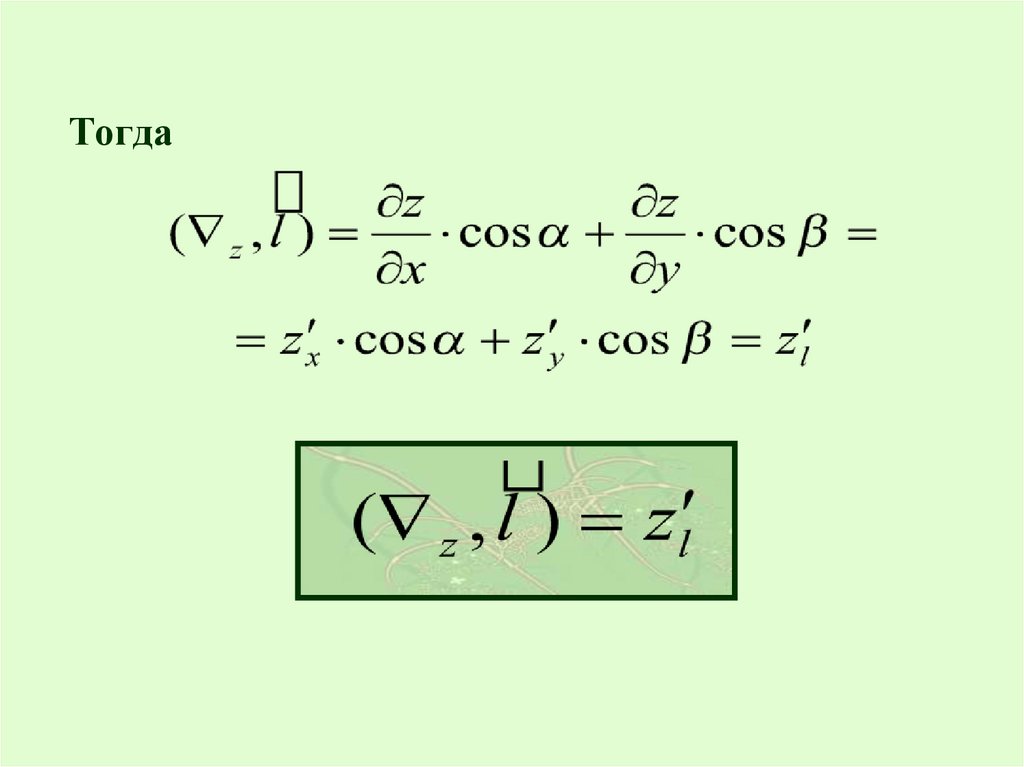










 Математика
Математика








