Лекция №2 (2). Основные теоремы электродинамики

1. Тема 1. ОСНОВНЫЕ УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ Лекция №2 (2). Основные теоремы электродинамики

1. Граничные условия на поверхностях раздела
реальных сред. Условия излучения.
2. Основные теоремы электродинамики.
3. Энергия электромагнитного поля. Теорема
Умова-Пойнтинга.
Электродинамика и РРВ.Сем.1. Лекция 2(2).
1

2. 1 Граничные условия на поверхности раздела реальных сред. Условия излучения

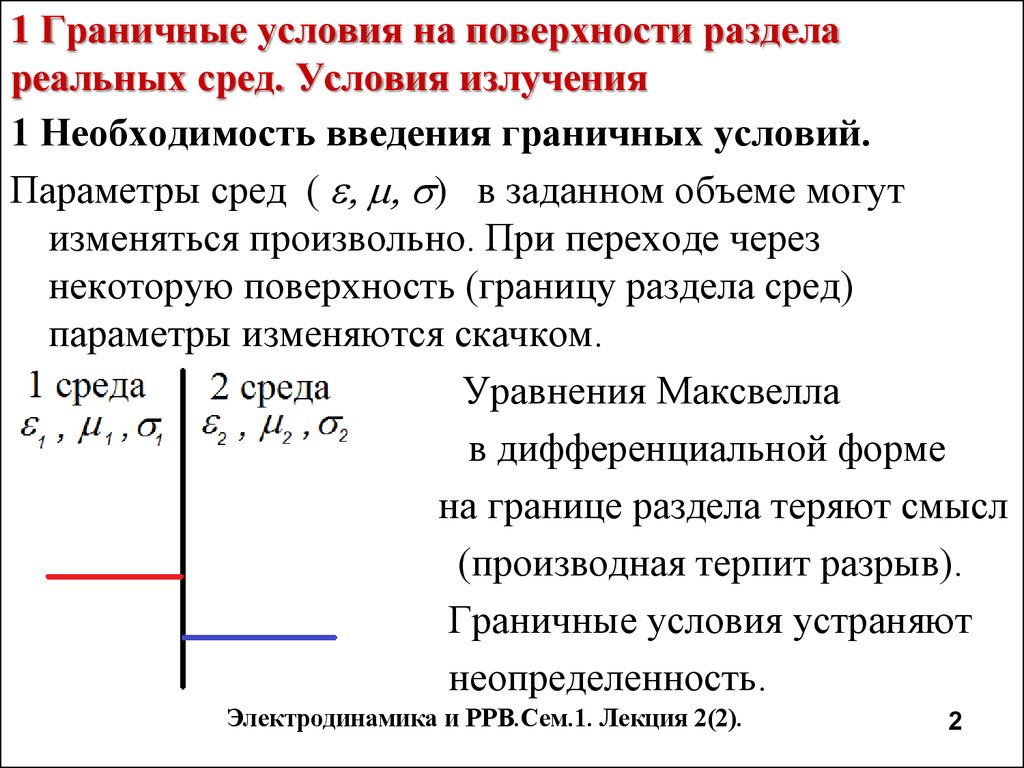
1 Необходимость введения граничных условий.
Параметры сред ( e, m, s) в заданном объеме могут
изменяться произвольно. При переходе через
некоторую поверхность (границу раздела сред)
параметры изменяются скачком.
Уравнения Максвелла
в дифференциальной форме
на границе раздела теряют смысл
(производная терпит разрыв).
Граничные условия устраняют
неопределенность.
Электродинамика и РРВ.Сем.1. Лекция 2(2).
2

3.

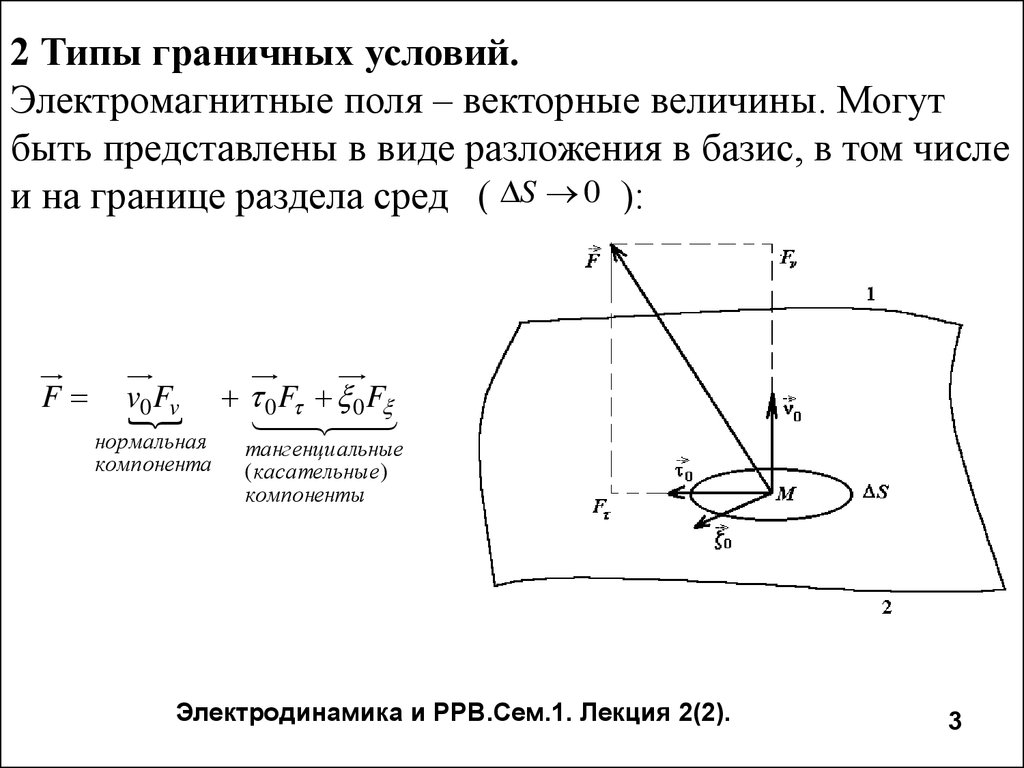
2 Типы граничных условий.
Электромагнитные поля – векторные величины. Могут
быть представлены в виде разложения в базис, в том числе
и на границе раздела сред ( S 0 ):
F
v0 Fv
нормальная
компонента
0 F 0 F
тангенциальные
( касательные )
компоненты
Электродинамика и РРВ.Сем.1. Лекция 2(2).
3

4.

Граничные условия для электрического поля:
D1 D 2 v0
- для нормальных компонент:
- для тангенциальных компонент: E1 E 2 0 [v , E1 E 2 ] 0
0
0
Электродинамика и РРВ.Сем.1. Лекция 2(2).
4

5.

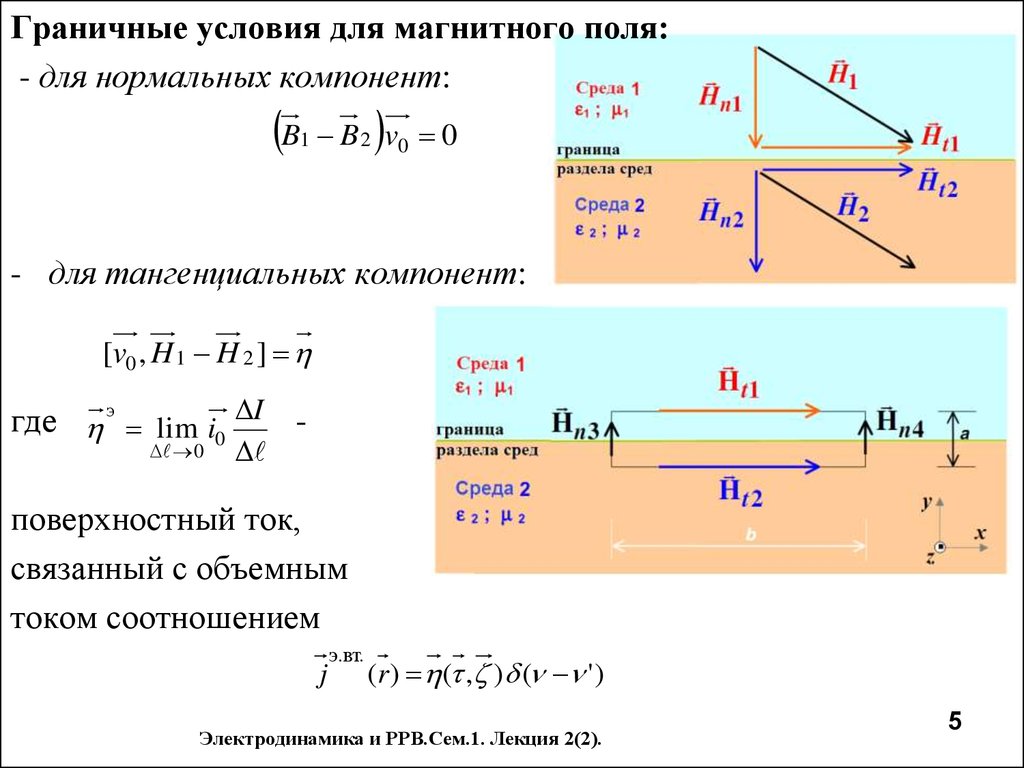
Граничные условия для магнитного поля:
- для нормальных компонент:
B
1
B 2 v0 0
- для тангенциальных компонент:
[v0 , H 1 H 2 ]
где э lim i0 I 0
поверхностный ток,
связанный с объемным
током соотношением
j
э.вт.
(r ) ( , ) ( ' )
Электродинамика и РРВ.Сем.1. Лекция 2(2).
5

6.

Условия излучения: применяются для обеспечения единственности
решения. (В общем случае решений дифференциальных
уравнений – два. Одно не соответствует физическим понятиям).
Для свободного пространства используется условие излучения
Зоммерфельда:
1) амплитуда поля на больших расстояниях от источника должно
убывать, по крайней мере, как обратная от данного расстояния
величина (│A│~1/r);
2) фаза поля должна быть такой же, как у уходящей на
бесконечность волны (φ~exp(-ikr)).
Для устранения неопределенности при изломах применяют условие
на ребре: E D H B dV 0 при dV 0 .
V'
Из условия следует, что в окрестности ребра ни одна из
составляющих ЭМП не может возрастать быстрее 1 ,
где - расстояние от ребра; 0 1
Электродинамика и РРВ.Сем.1. Лекция 2(2).
6

7.

2 Основные теоремы электродинамики
Используются для упрощения физической трактовки ряда явлений и
при решении ряда задач.
1. Теорема единственности:
Электромагнитное поле в любой момент времени в любой точке
объема определяется уравнениями Максвелла при заданных
источниках однозначно, если
- в каждой точке объема даны начальные значения векторов
напряженности электрического и магнитного полей;
- известны граничные значения касательных проекций одного из
векторов в точках поверхности S для любого момента времени.
Электродинамика и РРВ.Сем.1. Лекция 2(2).
7

8.

2. Лемма Лоренца: взаимодействие между полями в областях
- в дифференциальной форме
div[E1 , H 2 ] div[E 2 , H 1 ]
э ст
э ст
j1
м ст
j 2 E1 j 2
E2
м ст
j1
H2
H1
в интегральной форме
-
E1 , H 2 E 2 , H 1 d s
S
V1
j
ст.э
1
ст. м
E 2 j1
H 2 dv
j
ст.э
2
ст. м
E1 j 2
H 1 dv
V2
Электродинамика и РРВ.Сем.1. Лекция 2(2).
8

9.

Следствия леммы Лоренца:
– принцип взаимности:
j
ст.э
1
ст.м
E 2 j1
H 2 dv
V1
j
ст.э
2
ст.м
E1 j 2
H 1 dv
V2
Ограничение применимости – изотропные среды.
- теорема эквивалентных токов. Позволяет находить поле в
любой точке пространства при известном решении задачи
дифракции по полю вспомогательного диполя и известном
распределении полей на поверхности S:
для электрического источника
э
э
м
э
э
э
a E (r ) j E в j H в dv [n, H ] E в [n, E ] H в ds
V
S
для магнитного источника
э
м
м
м
м
м
b H (r ) j E в j H в dv [n, H ] E в [n, E ] H в ds
V
S
Эквивалентные токи:
э
J [n, H ]
м
J [n, E ]
Электродинамика и РРВ.Сем.1. Лекция 2(2).
9

10. 3 Энергия электромагнитного поля. Теорема Умова-Пойнтинга

3 Энергия электромагнитного поля. Теорема УмоваПойнтинга
Сторонний источник – источник, который возбуждает ЭМП, но
сам от него не зависит.
ЭМП является носителем энергии. В выделенном объеме энергия
может изменяться во времени за счет двух процессов:
• превращения электромагнитной энергии в другие формы энергии
(тепловая энергия, химическая энергия, кинетическая энергия
ускоренных частиц и т.д.) и наоборот;
• вытекания и втекания электромагнитной энергии из данного
объема через поверхность S, ограничивающую данный объем.
dw
P
pст
dt
где pст - мощность поля, создаваемого сторонними источниками;
dw / dt - мощность, идущая на изменение энергии ЭМП;
- мощность поля, выходящая через поверхность S.
Электродинамика и РРВ.Сем.1. Лекция 2(2).
10

11.

Теорема Умова-Пойнтинга – уравнение баланса энергии.
- в дифференциальной форме:
2
2
ст
E
H
s
E
e 0e
m0 m
div[
E ,
H
]
Ej
t
2
2
нагрев
энергия стороннего
проход
вещества
энергии
источника
2
колебательные
процессы
-
(излучение )
в интегральной форме:
B
э.ст.
D
s E dv H t E t dv [ E, H ] d s j Edv
V
V
S
V
2
Определения:
- отдаваемая мощность: P j Edv
V
-
мощность излучения:
[ E, H ] d s
S
-
вектор Пойнтинга:
[E, H ]
Электродинамика и РРВ.Сем.1. Лекция 2(2).
11

12.

Физическая трактовка уравнения баланса энергии.
Первое слагаемое – работа, совершаемая ЭМП (в том числе и на
нагрев вещества).
Второе слагаемое - колебательные процессы - связано с процессом
перехода энергии электрического поля
в магнитное
e0
1
W e E dv D E dv
2V
2V
э
m0
2
1
W
m H dv B H dv
2 V
2V
м
2
и наоборот.
Третье слагаемое описывает поток энергии или мощность
излучения через замкнутую поверхность S.
Баланс считается активным, если преобладает отдача энергии во
внешнее пространство 0 .
Баланс считается пассивным, если преобладает поглощение
энергии из внешнего пространства 0.
Баланс нейтрален, если 0 .
Электродинамика и РРВ.Сем.1. Лекция 2(2).
12