Похожие презентации:
Электростатика. Основные теоремы (в вакууме)
1. ЭЛЕКТРОСТАТИКА основные теоремы (в вакууме)
2. 1. ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА НАПРЯЖЕННОСТИ ПОЛЯ
21 2 Edl .
Для обхода по замкнутому контуру
E dl 0
1
1 2
и мы получаем, что
теорема о циркуляции в интегральной форме
L
Циркуляция вектора напряженности электростатического поля
равна нулю.
Это утверждение отражает потенциальность электростатического поля.
rotE 0
E 0
теорема о циркуляции в диф. форме
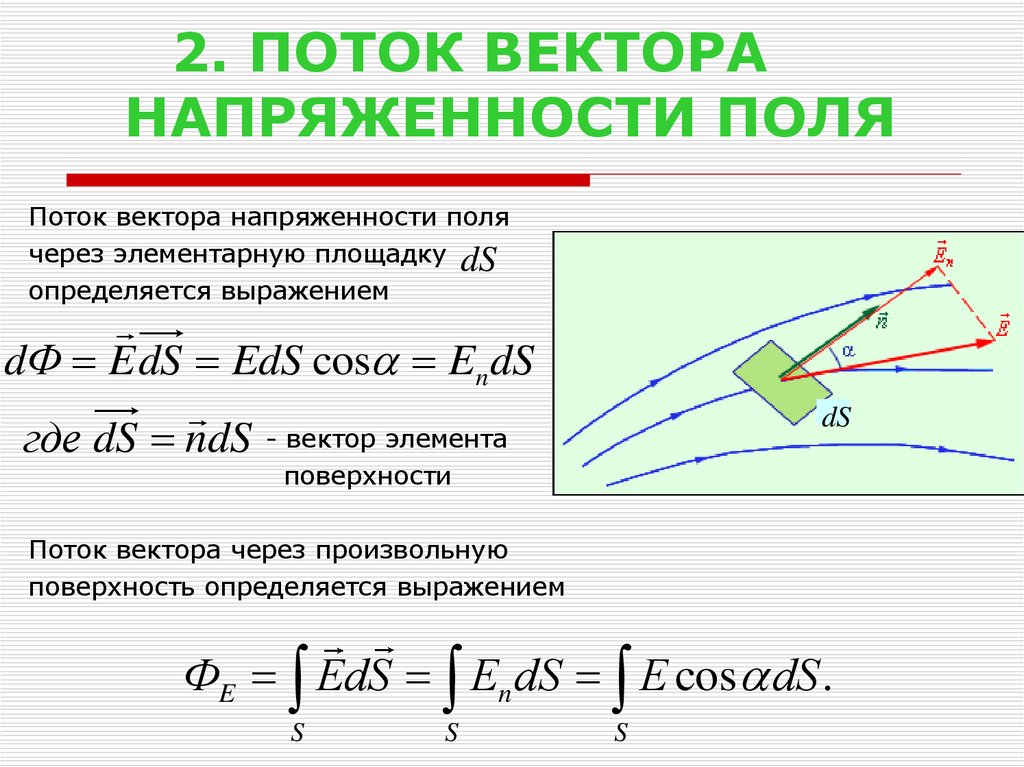
3. 2. ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ ПОЛЯ
Поток вектора напряженности полячерез элементарную площадку dS
определяется выражением
dФ E dS EdS cos En dS
где dS ndS - вектор элемента
dS
поверхности
Поток вектора через произвольную
поверхность определяется выражением
ФE EdS En dS E cos dS .
S
S
S
4. 3. ТЕОРЕМА ГАУССА
1E
dS
3. ТЕОРЕМА ГАУССА
S
q
i
0
Поток вектора напряженности электростатического
поля сквозь любую замкнутую поверхность равен
алгебраической сумме зарядов, находящихся внутри этой
поверхности, деленной на 0.
Теорема Гаусса устанавливает фундаментальное
свойство ЭП – наличие у него источников (и стоков)
линий поля.
div E
0
или
E .
0
5. 4. УРАВНЕНИЕ ПУАССОНА
.0
2
2
2
2
2
2 i
j k 2 2 2
y
z x y
z
x
5. ПОЛЕ ЗАРЯЖЕННОЙ СФЕРЫ
r
R q r 0 E dS 0 Er (r )dS 0
S
R
S
Er (r ) 0.
r R Er r dr 0 (r ) ( R) 0 .
r
1 q0
kq0
. (r)
.
r R Er r
2
r
4 0 r
6. ГРАФИКИ ПОЛЯ ЗАРЯЖЕННОЙ СФЕРЫ
Er (r )r (r )
R
R
r
r
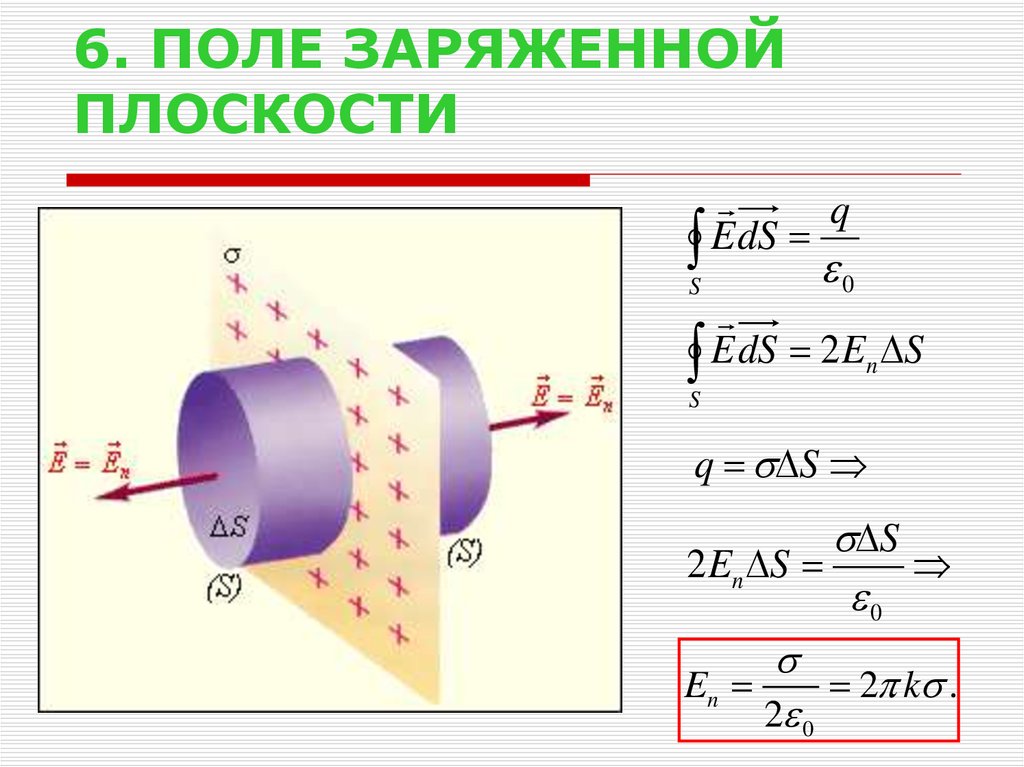
7. 6. ПОЛЕ ЗАРЯЖЕННОЙ ПЛОСКОСТИ
qE dS
S
0
E dS 2 En S
S
q S
S
2 En S
0
En
2 k .
2 0
8. 7. ПОЛЕ ЗАРЯЖЕННОЙ ПРЯМОЛИНЕЙНОЙ НИТИ
1Er ( r )
2k
2 0 r
r
(r 0).
r2
( r1 ) ( r2 ) 2k ln
r1
9. 8. ОСНОВНЫЕ ТЕОРЕМЫ ЭП В ВАКУУМЕ
ТЕОРЕМА ГАУССАИФ
1
E dS
S
ДФ
ТЕОРЕМА О
ЦИРКУЛЯЦИИ
E dl 0
dV
0 V
E .
0
L
E 0







 Физика
Физика








