применение интеграла - конкурс

1.

ГОУ СПО «Ижевский индустриальный техникум»
Применение интеграла
при обучении профессии станочник
(фрезерное дело)
(электронное учебное пособие)
Номинация: Разработка информационной или
обучающей презентации по изучаемой дисциплине
Авторы: Лекомцев Никита Викторович, 131 группа, 3 курс,
профессия станочник (металлообработка)
Зорин Владимир Сергеевич, 131 группа, 3 курс,
профессия станочник (металлообработка)
Руководители: Касаткина Инга Сергеевна, преподаватель математики,
Бахтина Ольга Петровна, мастер п/о
E-mail: [email protected]
г. Ижевск, 2011

2. Цели проекта:

• Исследовать возможность применения знаний по
математики на занятиях по фрезерной обработке
• Создать электронное учебное пособие, позволяющие
систематизировать знания учащихся по темам
«Интегральное исчисление» и «Фрезерная
обработка».
Данное пособие можно использовать как при
проведении уроков математики и фрезерного дела
(частично), так и при проведении бинарных уроков и
самостоятельной подготовки учащихся.
• Создать банк практикоориентированных задач для
выполнения творческих заданий.

3. Структура электронного учебного пособия

Пособие состоит из трех частей:
•Интегральное исчисление (теоретический материал)
•Фрезерование (фрезерная обработка криволинейных поверхностей)
(теоретический материал)
•Задачи с практическим содержанием
Все учебное пособие снабжено гиперссылками, позволяющими легко
находить интересующий материал. Так как наше пособие можно
использовать как при изучении нового материала, так и при повторении
пройденного, смена слайдов осуществляется по щелчку, позволяя
работать с материалом в любом темпе.
Немного изменяя анимацию, преподаватель имеет возможность
использовать теоретический материал как при изучения нового, так и для
контроля.
В данном учебном пособии представлен видеофрагмент «Изготовление
подставки», демонстрирующий работу на круглом поворотном столе.

4. Применение интеграла

ГОУ СПО «Ижевский индустриальный техникум»
Применение интеграла
при обучении профессии
станочник
«Как и другие науки, математика
возникла из практических нужд
людей: из измерения площадей
земельных участков и вместимости
сосудов, из счисления времени и их
механики.»
Ф. Энгельс
Авторы: Лекомцев Никита, гр. 131
Зорин Владимир, гр. 131
Руководители: Касаткина Инга Сергеевна
Бахтина Ольга Петровна

5. Содержание

• Интегральное исчисление.
понятия и формулы)
(основные
• Фрезерование (фрезерная обработка
криволинейных поверхностей)
• Задачи

6.

• Первообразная
• Таблица первообразных
• Правила нахождения первообразной
• Неопределенный интеграл
• Определенный интеграл
• Геометрический смысл определенного
интеграла
• Некоторые применения интеграла

7. Интегральное исчисление. Основные определения.

называется первообразной для функции f x
Определение: Дифференцируемая функция F x
на заданном промежутке, если для всех x из этого
промежутка справедливо равенство
F x f x

8.

Таблица первообразных
функция
первообразная
f(x)
F(x)
f(x)
F(x)
k (постоянная)
kx+C
5
5x+C
x (n , n 1)
x n 1
C
n 1
7
x 7 1
x8
C
C
7 1
8
1
x
2 x C
sin x
- cos x +C
cos x
sin x + C
n
1
cos 2 x
1
sin 2 x
tg x + C
- ctg x + C
пример
x

9.

Три правила нахождения первообразных
Правило 1.
Если F есть первообразная для f(x), а G –
первообразная g(x), то F+G есть первообразная
для f+g.
ПРИМЕР
Пример 1: Найти общий вид первообразных
3 + соs x
4
для функции
f(x)=
х
х
F(х) =
4
sin x.
(Находим по таблице первообразные для каждого слагаемого)

10. Правило 2.

Если F есть первообразная для f(x), а k –
постоянная, то kF есть первообразная для kf(х).
Пример
2: Найти общий вид первообразных
ПРИМЕР
для функции f(x)= 3 sin x.
F(x) = 3∙ (- cos x) + C = -3cos x + C.
(Найденную по таблице первообразную умножаем на
постоянный множитель)

11. Правило 3.

Если F(х) есть первообразная для f(x), а k и b –
1
постоянные, причем k 0, то
F ( kx b)
k
есть первообразная для f(kх+b).
Пример
3: Найти общий вид первообразных для
ПРИМЕР
функции f(x)=sin (3x-2).
1
F(x)= cos(3x 2) С
3
(Первообразная sin x равна - cos x).

12. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Совокупность всех первообразных F(x)+С
для функции f(x) на рассматриваемом промежутке
называется неопределенным интегралом и
обозначается
f x dx F x c
где f(x) – подинтегральная функция,
f(x)dx – подинтегральное выражение
(дифференциал),
х – переменная интегрирования.

13. Свойства неопределенного интеграла

1)
f ( x)dx f ( x)
2)
k
f
x
dx
k
f
x
dx
3)
f
x
g
x
dx
f
x
dx
g
x
dx

14.

Определенным интегралом называется
приращение
F(b)-F(a)
любой
из
первообразных
функций
F(х)+С
при
изменениии аргумента от х=a до х=b
b
f x dx F (b) F (a) –
a
формула Ньютона – Лейбница

15. Алгоритм нахождения определенного интеграла

b
f x dx
a
1. Найти первообразную функции F x для функции .f x
2. Вычислить значение F x при х= b (b называется
верхним пределом)
3. Вычислить значение F x при х= а (а называется
нижним пределом)
4. Вычислить разность
F (b) F (a)

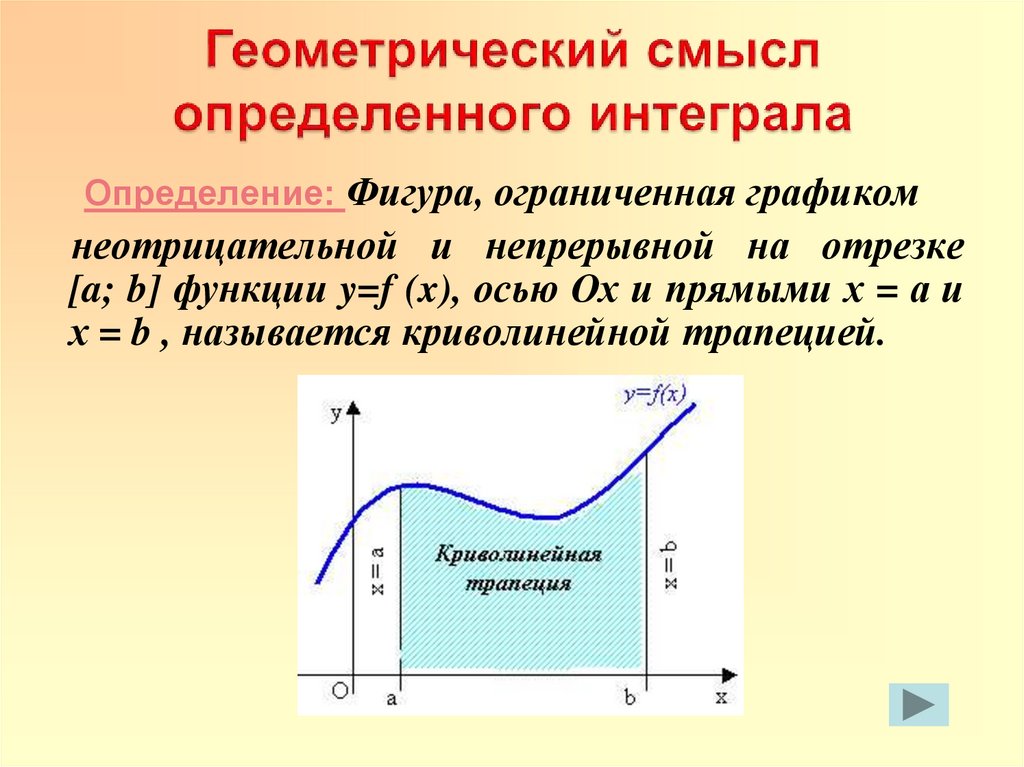
16. Геометрический смысл определенного интеграла

Определение: Фигура, ограниченная графиком
неотрицательной и непрерывной на отрезке
[a; b] функции y=f (x), осью Ох и прямыми х = а и
х = b , называется криволинейной трапецией.

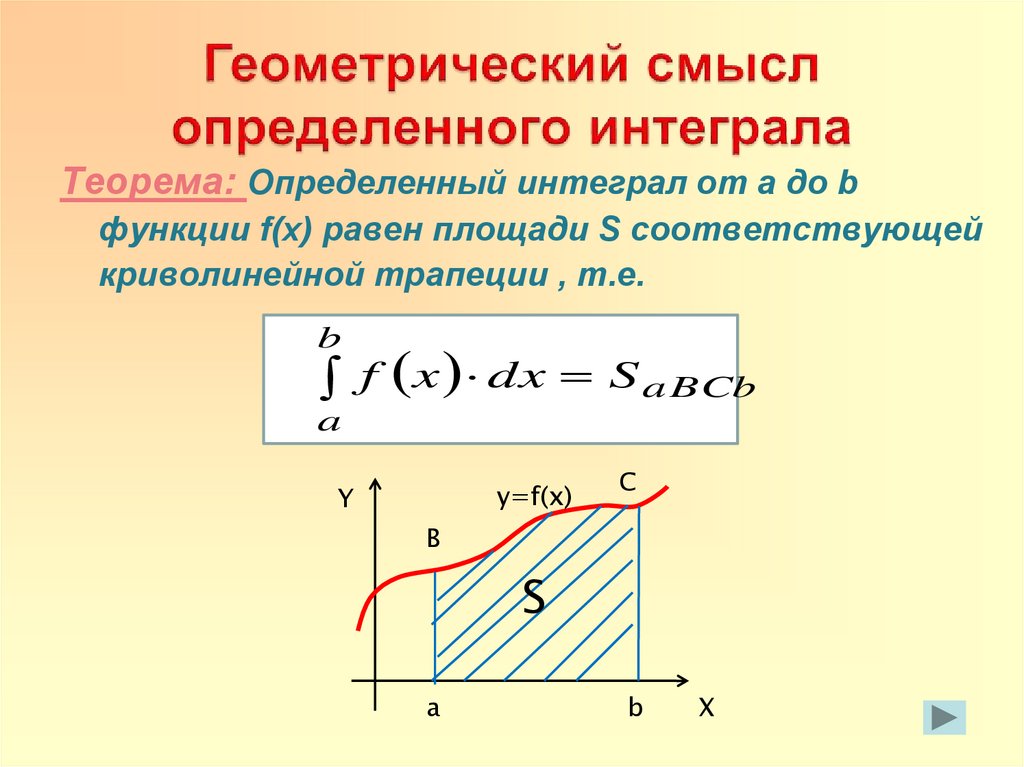
17. Геометрический смысл определенного интеграла

Теорема: Определенный интеграл от a до b
функции f(x) равен площади S соответствующей
криволинейной трапеции , т.е.
b
f x dx S aBCb
a
y=f(x)
Y
C
B
S
а
b
X

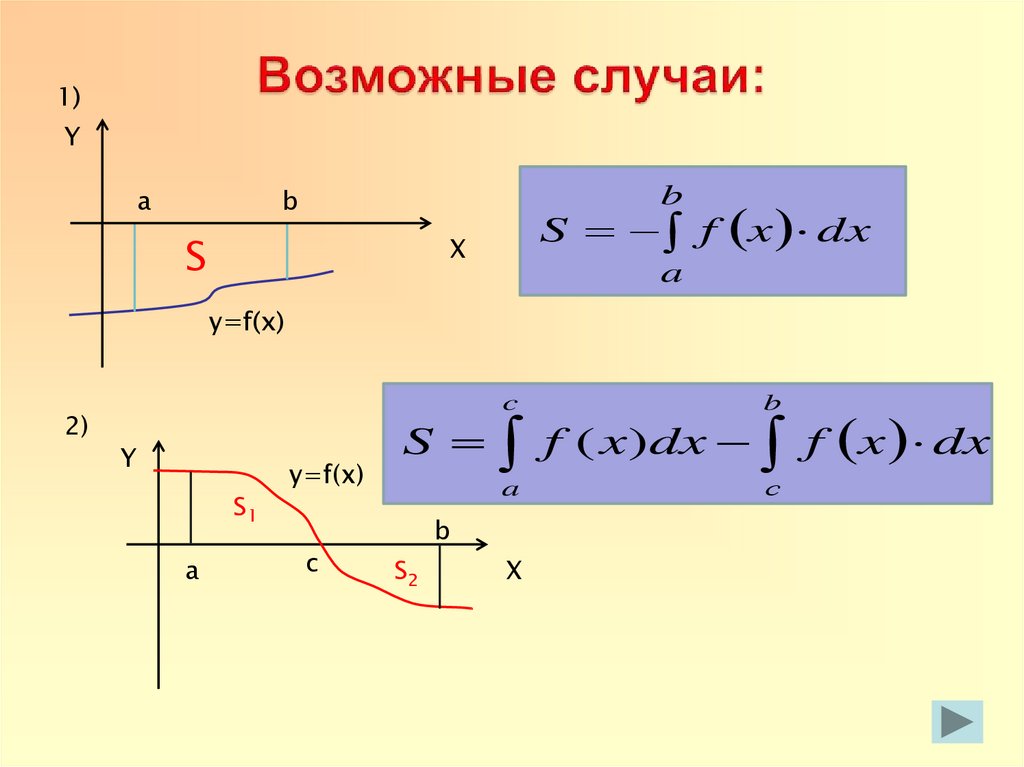
18. Возможные случаи:

1)
Y
a
b
b
S
S f x dx
X
a
y=f(x)
2)
Y
S1
a
y=f(x)
c
c
b
a
с
S f ( x)dx f x dx
b
S2
X

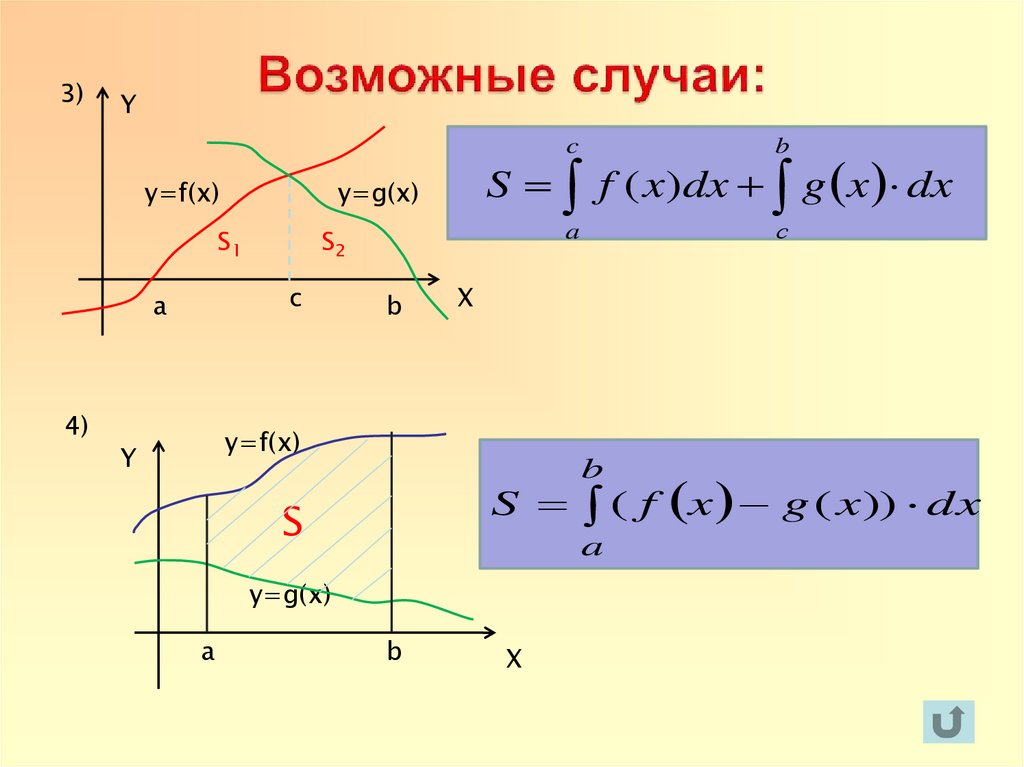
19. Возможные случаи:

3)
Y
y=f(x)
4)
S2
c
a
b
b
a
с
S f ( x)dx g x dx
y=g(x)
S1
c
X
y=f(x)
Y
b
S ( f x g ( x )) dx
S
a
y=g(x)
a
b
X

20. Некоторые применения интеграла

• Вычисление объемов тел
• Вычисление площадей
криволинейных поверхностей

21. Вычисление объемов

b
На практике мы вытачивали
наконечник для
2
украшения ограды.
V f ( x ) dx
Найдем его объем.
a
Уравнение полуокружности
y R2 x2
d 58мм R 29 мм
y 292 x 2
10
Y
-R
0
-10
R 10
R
29
29
29
V ( 29 2 x 2 ) 2 dx (841 x 2 ) dx
R
X
-10
29
29
х
(841х
)
102108,61( мм 3 )
3 29
3
102,1(см 3 )

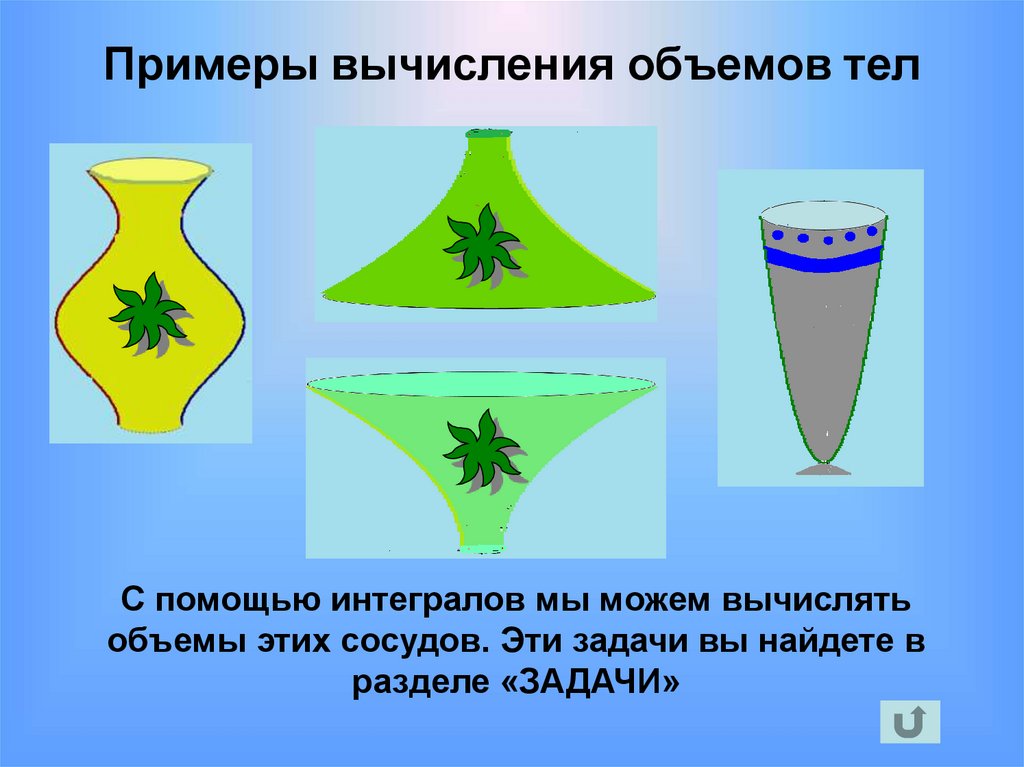
22. Примеры вычисления объемов тел

С помощью интегралов мы можем вычислять
объемы этих сосудов. Эти задачи вы найдете в
разделе «ЗАДАЧИ»

23. Задачи

Вычисление
площадей
криволинейных
поверхностей
Вычисление
объемов тел
вращения

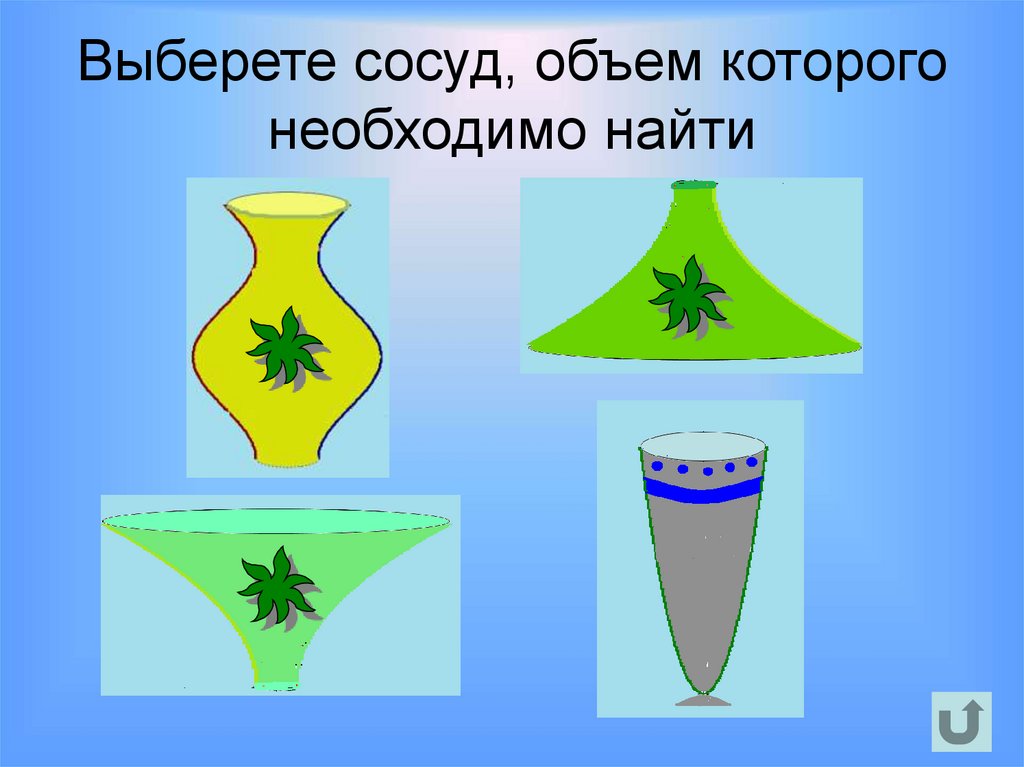
24.

Выберете сосуд, объем которого
необходимо найти

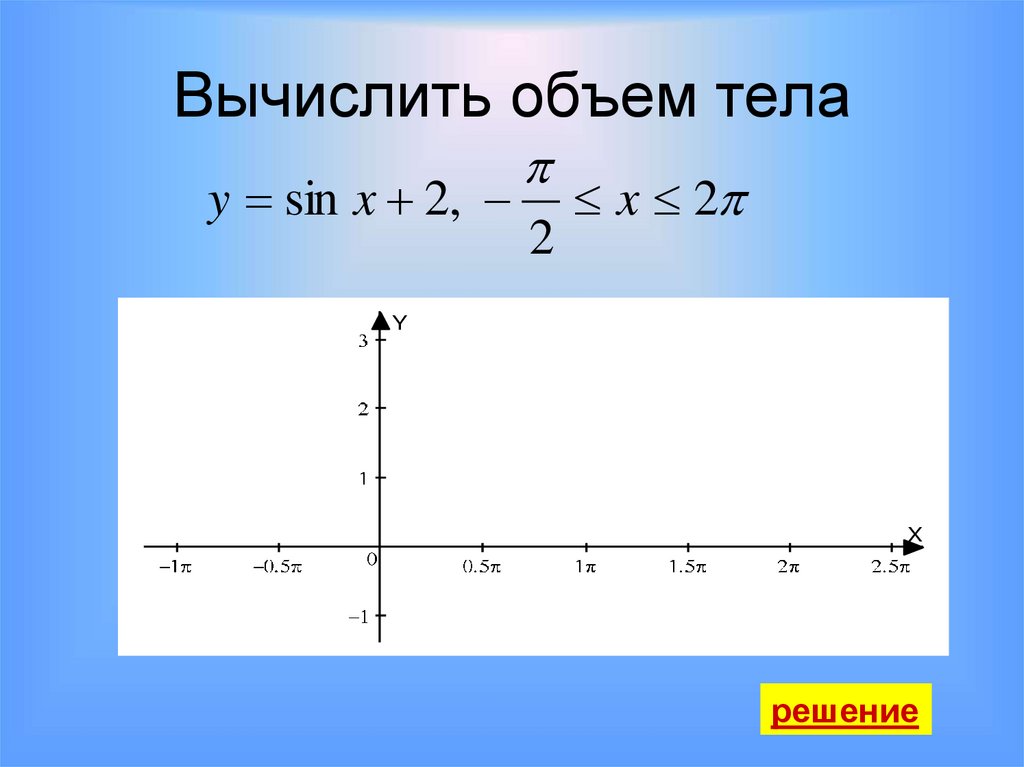
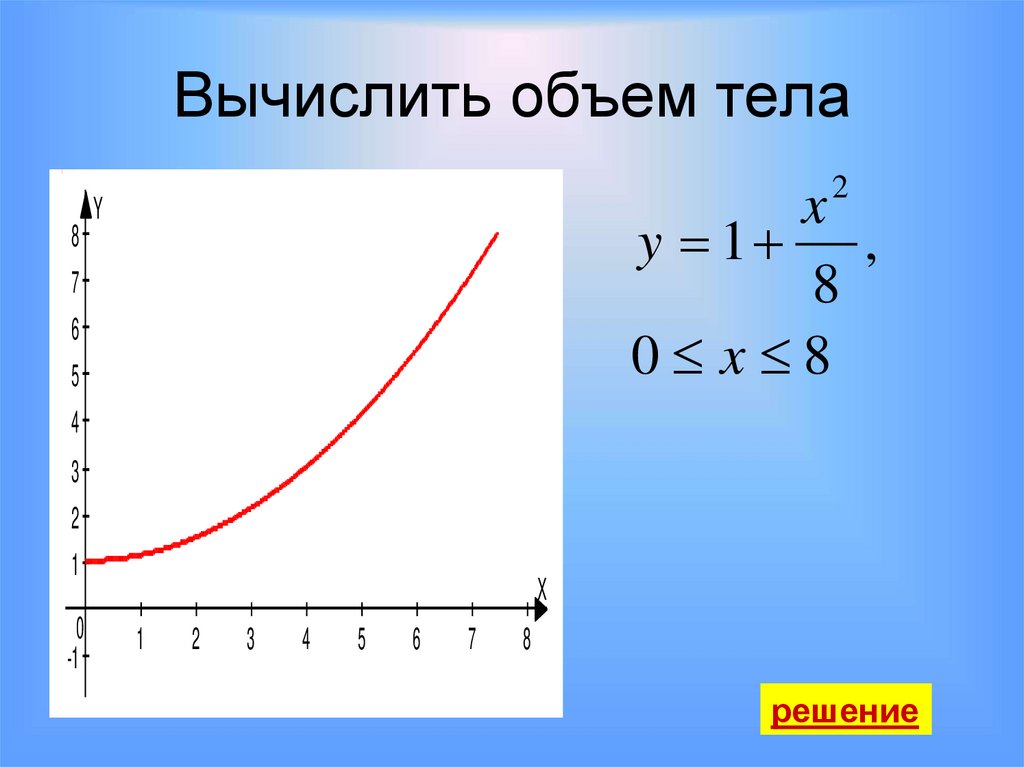
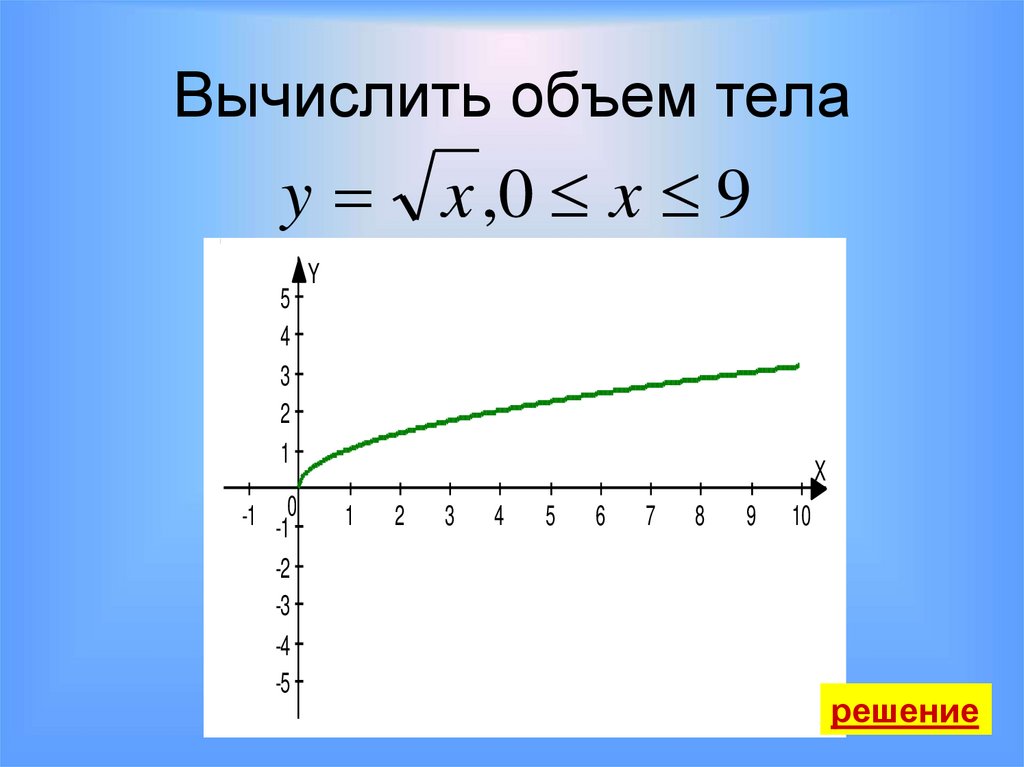
25. Вычислить объем тела

y sin x 2,
2
x 2
Y
X
решение

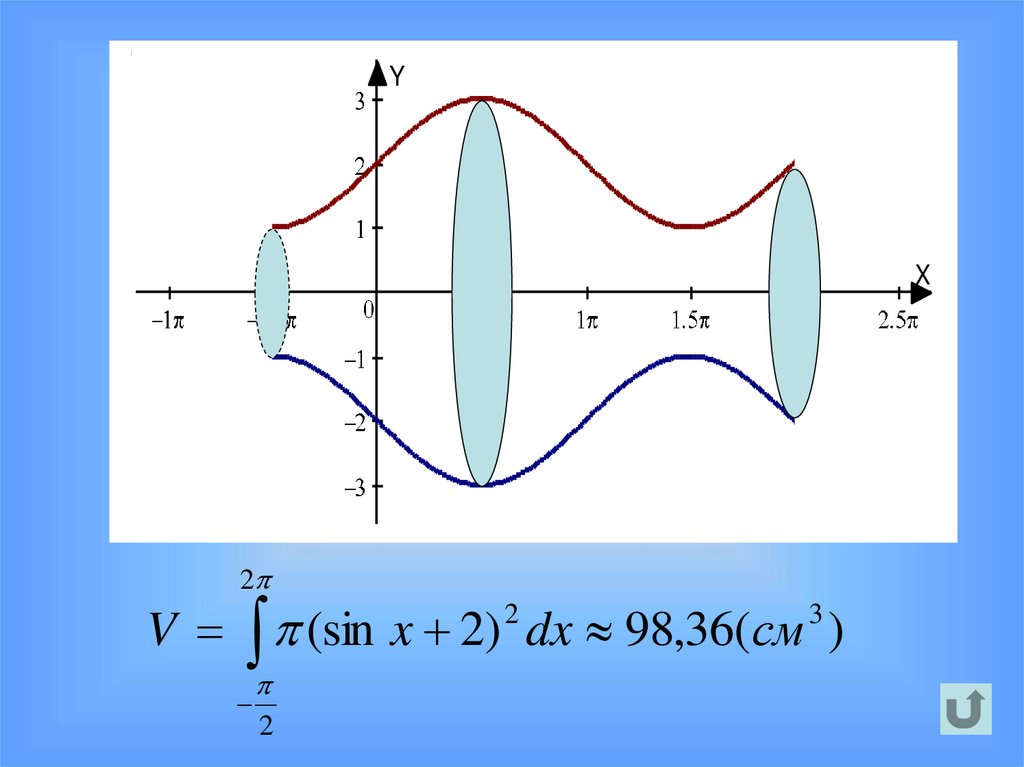
26.

Y
X
2
V (sin x 2) dx 98,36(см )
2
2
3

27. Вычислить объем тела

8
2
x
y 1 ,
8
0 x 8
Y
7
6
5
4
3
2
1
0
-1
X
1
2
3
4
5
6
7
8
решение

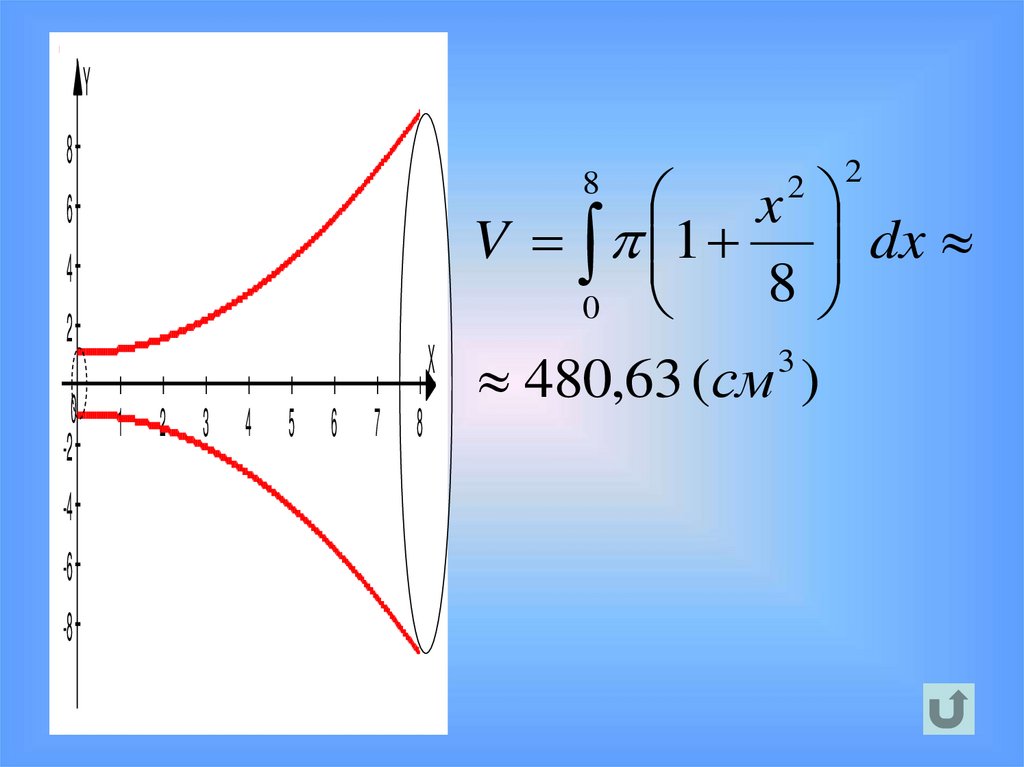
28.

Y
8
6
4
2
0
-2
-4
-6
-8
1 2 3 4 5 6 7 8
2
x
V 1 dx
8
0
3
X
480,63 (см )
8
2

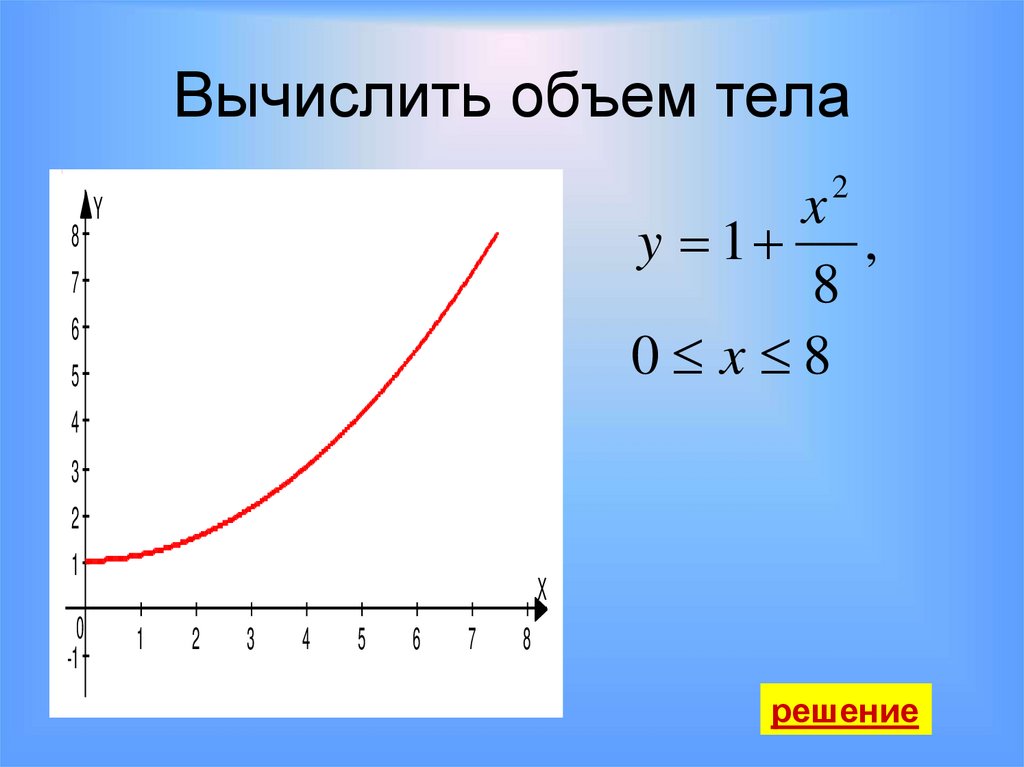
29. Вычислить объем тела

8
2
x
y 1 ,
8
0 x 8
Y
7
6
5
4
3
2
1
0
-1
X
1
2
3
4
5
6
7
8
решение

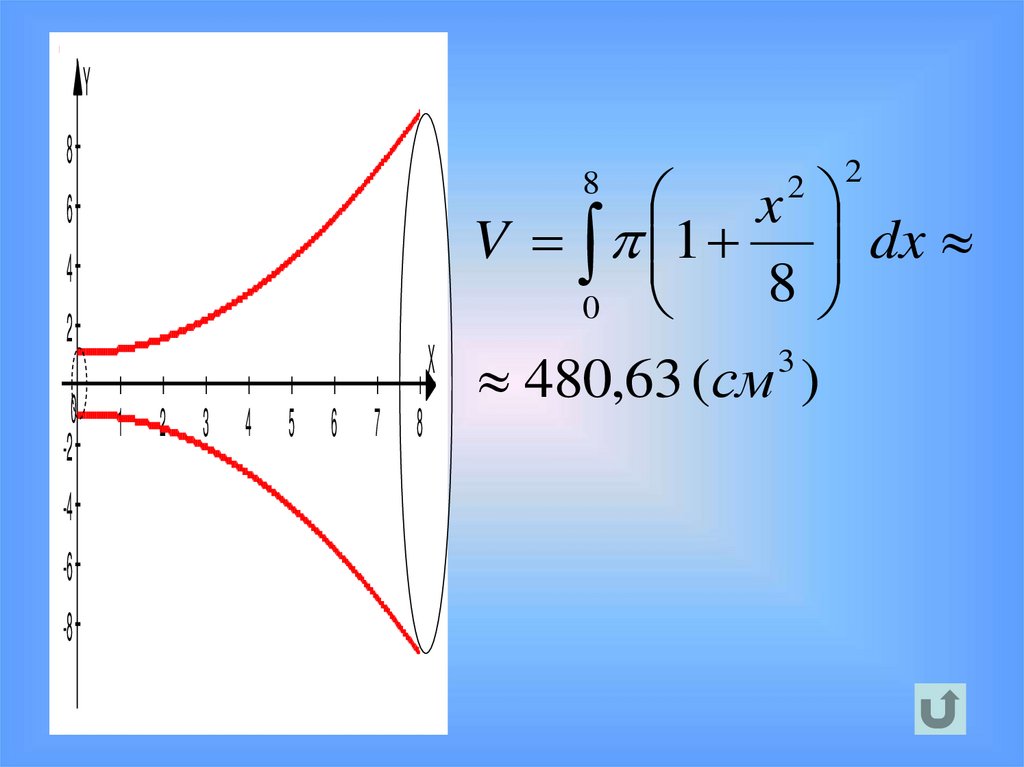
30.

Y
8
6
4
2
0
-2
-4
-6
-8
1 2 3 4 5 6 7 8
2
x
V 1 dx
8
0
3
X
480,63 (см )
8
2

31. Вычислить объем тела

y x ,0 x 9
5
4
3
2
1
-1 -10
-2
-3
-4
-5
Y
X
1
2
3
4
5
6
7
8
9
10
решение

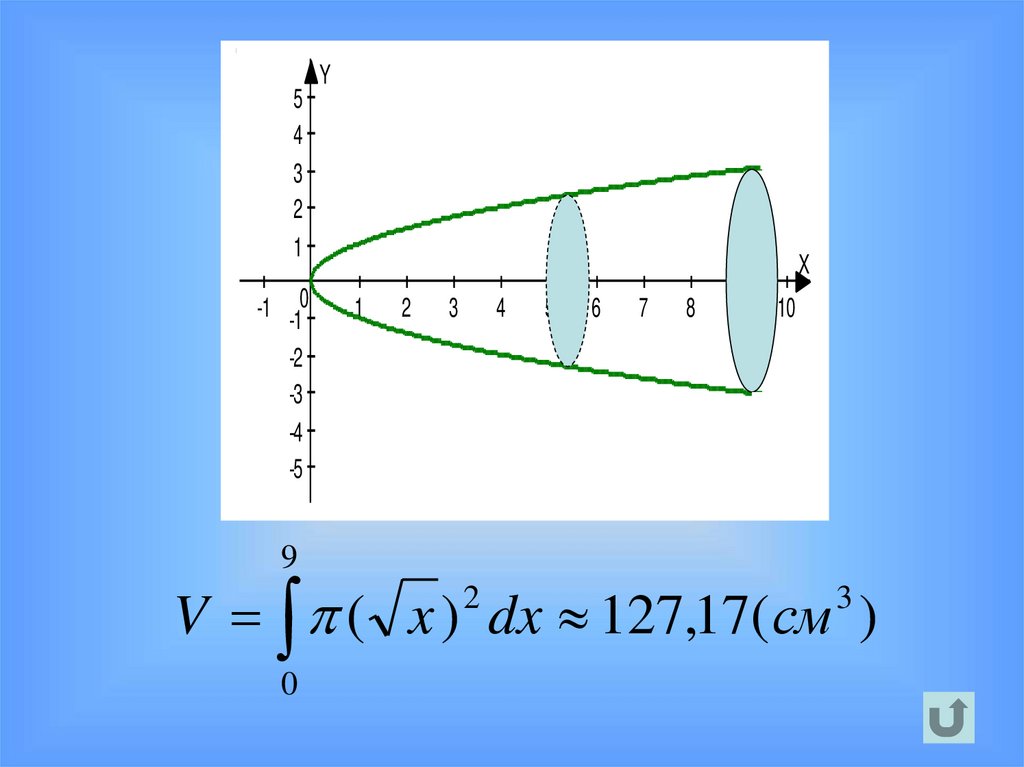
32.

5
4
3
2
1
-1 -10
Y
X
1
2
3
4
5
6
7
8
9
10
-2
-3
-4
-5
9
V ( x ) dx 127,17(см )
2
0
3

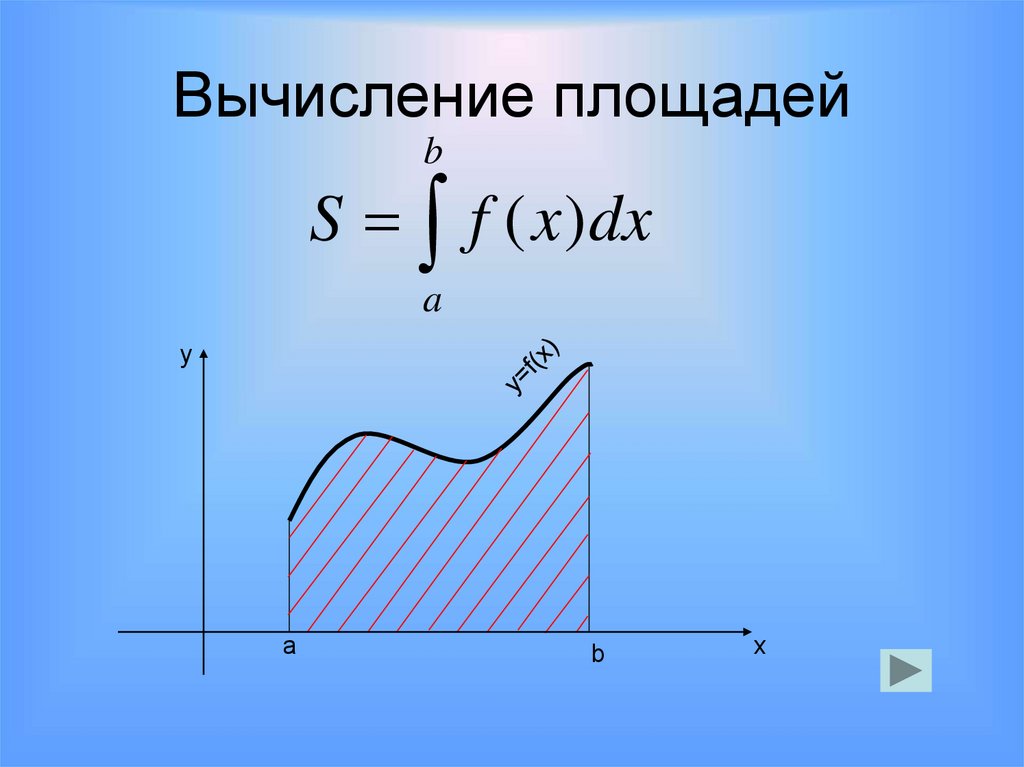
33. Вычисление площадей

b
S f ( x ) dx
a
у
a
b
х

34. Примеры вычисления площадей

Нам
необходимо
вычислить
площадь
подставки
под горячее
Сформулируем и
решим задачу
Решение

35.

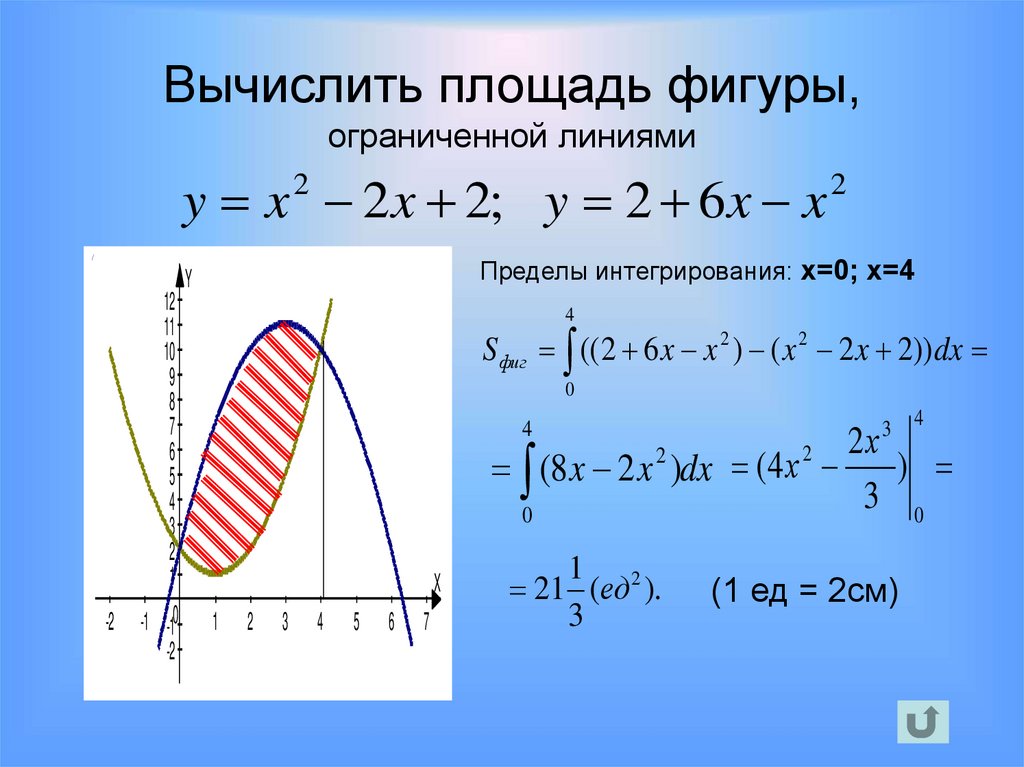
Вычислить площадь фигуры,
ограниченной линиями
y x 2 x 2; y 2 6 x x
2
12
11
10
9
8
7
6
5
4
3
2
1
-2
-1 -10
-2
2
Пределы интегрирования: х=0; х=4
Y
4
Sфиг (( 2 6 x x 2 ) ( x 2 2 x 2)) dx
0
4
2х
(8 x 2 x )dx (4 х )
3 0
0
4
3
2
X
1
2
3
4
5
6
7
1 2
21 (ед ).
3
2
(1 ед = 2см)

36. Вычисление площадей криволинейных поверхностей

• Задача 1
• Задача 2
• Задача 3

37.

Вычислить площадь фигуры,
ограниченной линиями:
y cos x 1; y 2 cos x 2; - x
Y
X
решение

38.

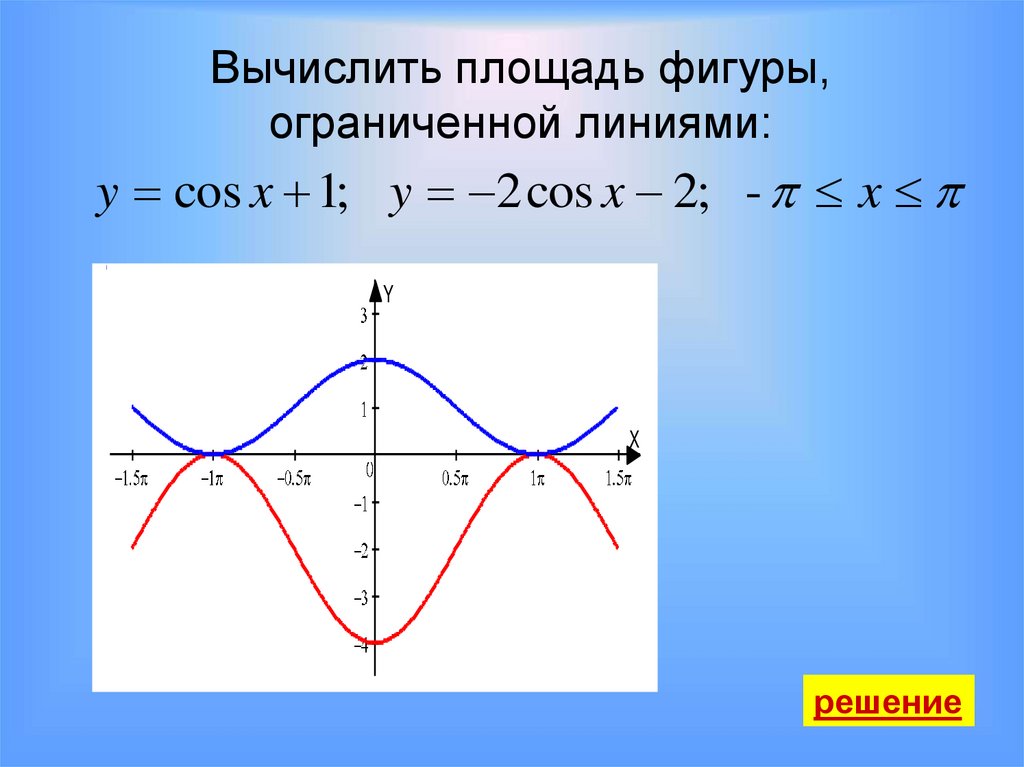
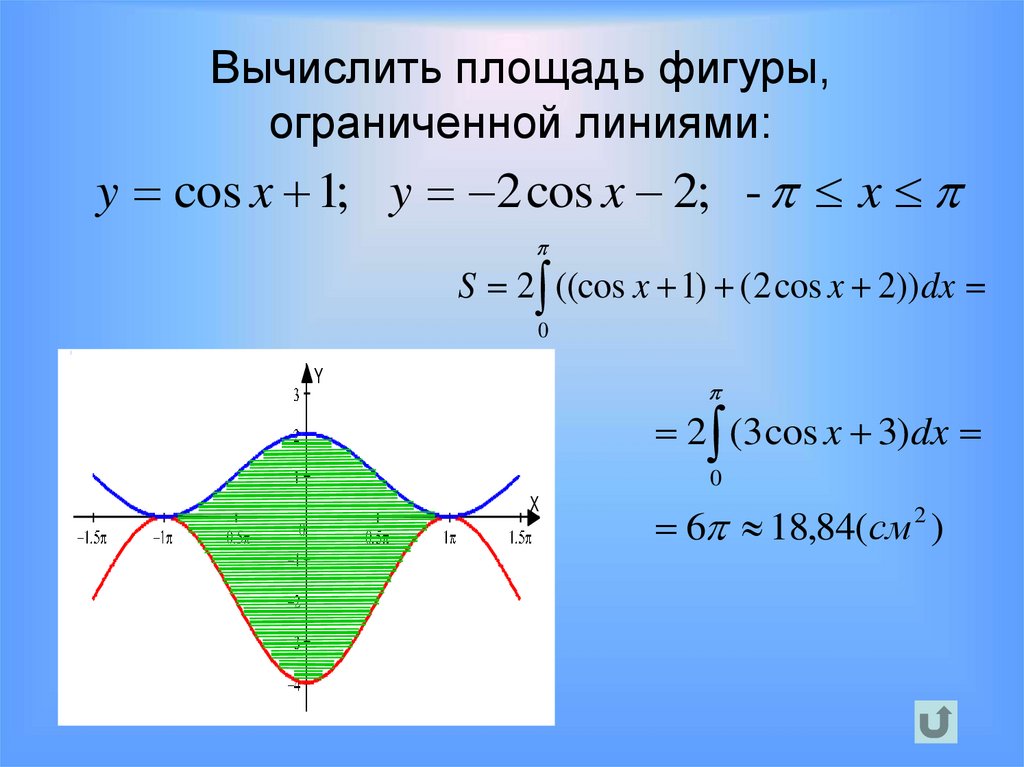
Вычислить площадь фигуры,
ограниченной линиями:
y cos x 1; y 2 cos x 2; - x
S 2 ((cos x 1) ( 2 cos x 2)) dx
0
Y
2 (3 cos x 3)dx
0
X
6 18,84(см 2 )

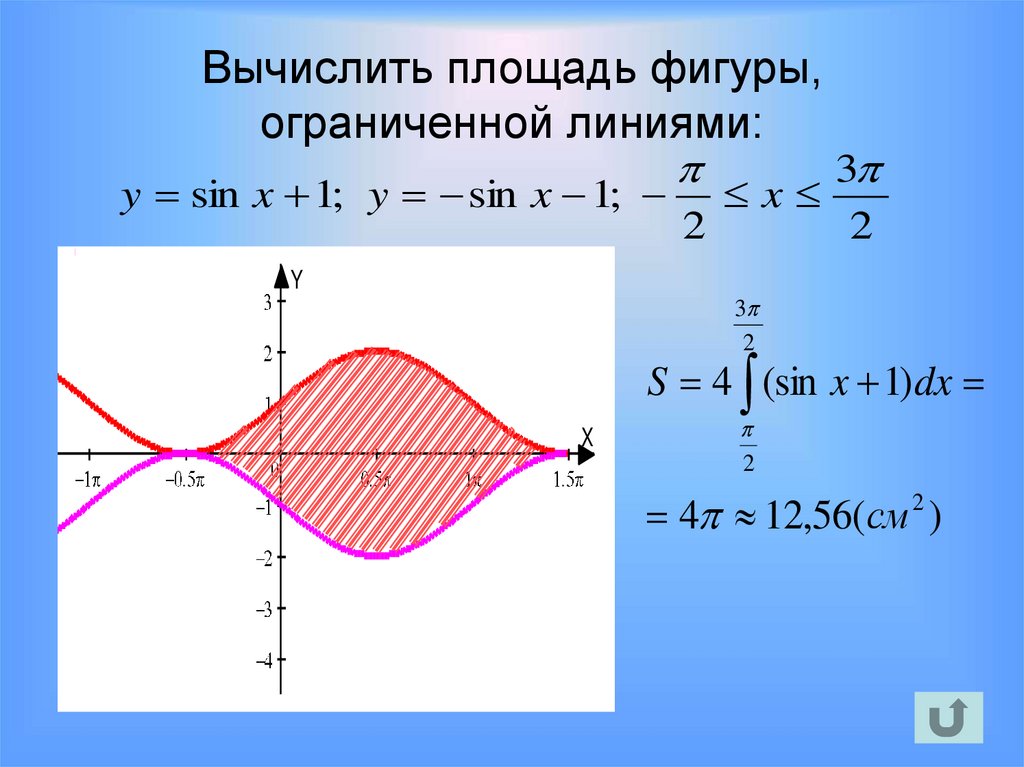
39.

Вычислить площадь фигуры,
ограниченной линиями:
3
y sin x 1; y sin x 1; x
2
2
Y
X
решение

40.

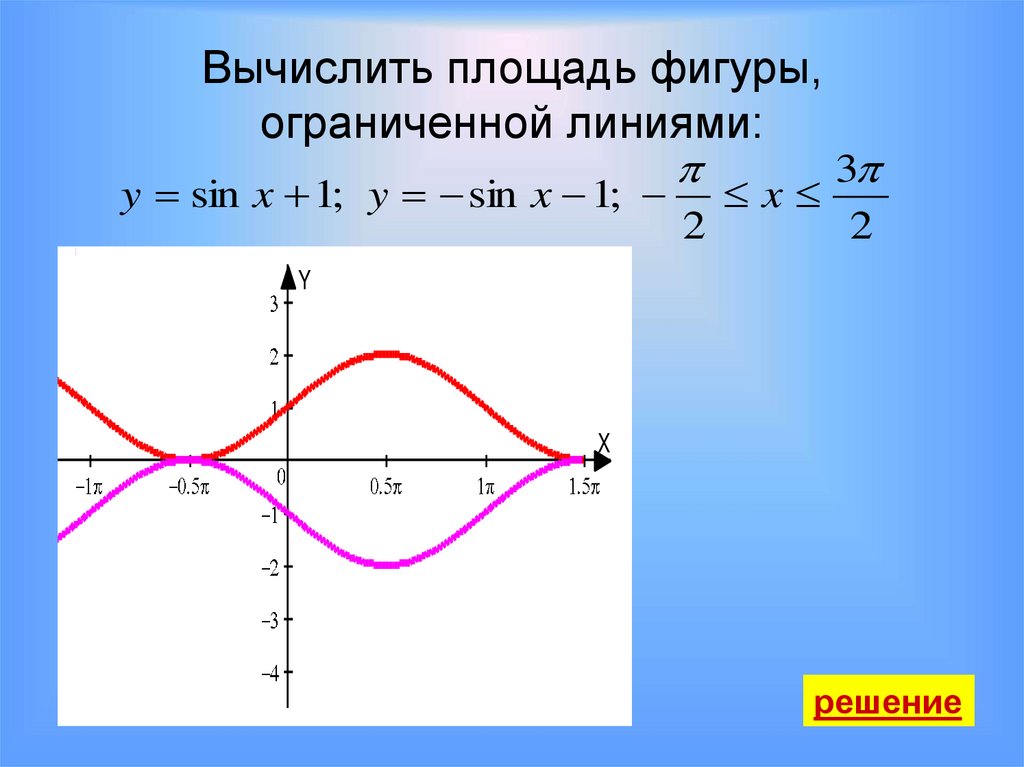
Вычислить площадь фигуры,
ограниченной линиями:
3
y sin x 1; y sin x 1; x
2
2
Y
3
2
S 4 (sin x 1)dx
X
2
4 12,56(см 2 )

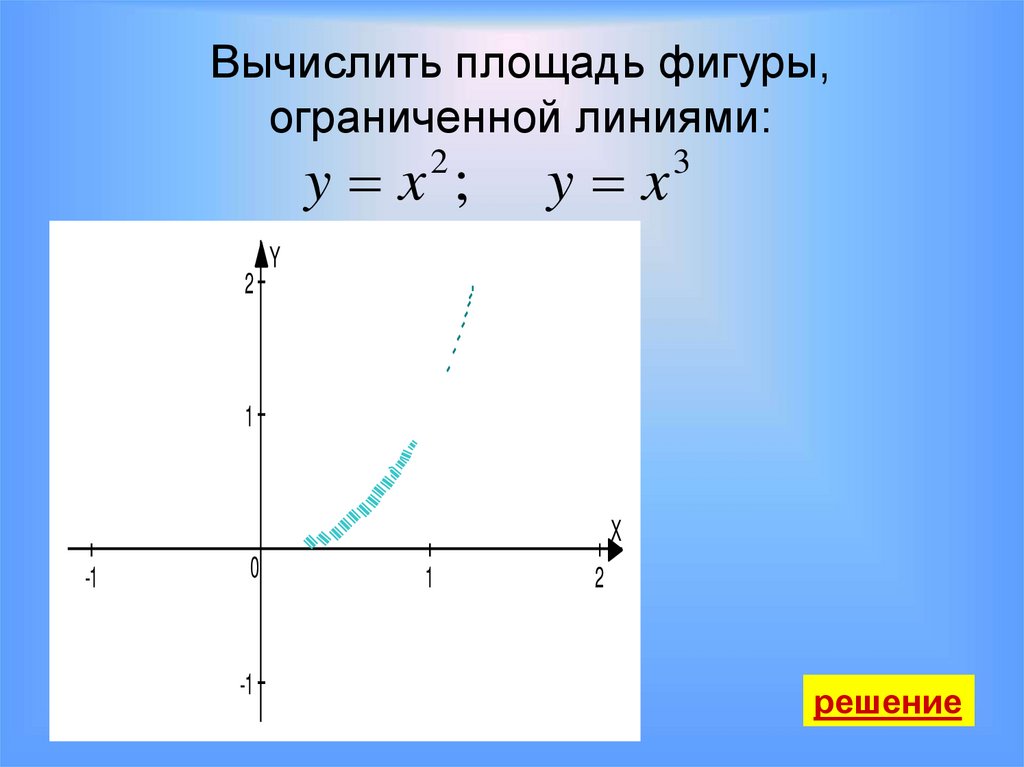
41.

Вычислить площадь фигуры,
ограниченной линиями:
y x ;
2
2
y x
3
Y
1
X
-1
0
-1
1
2
решение

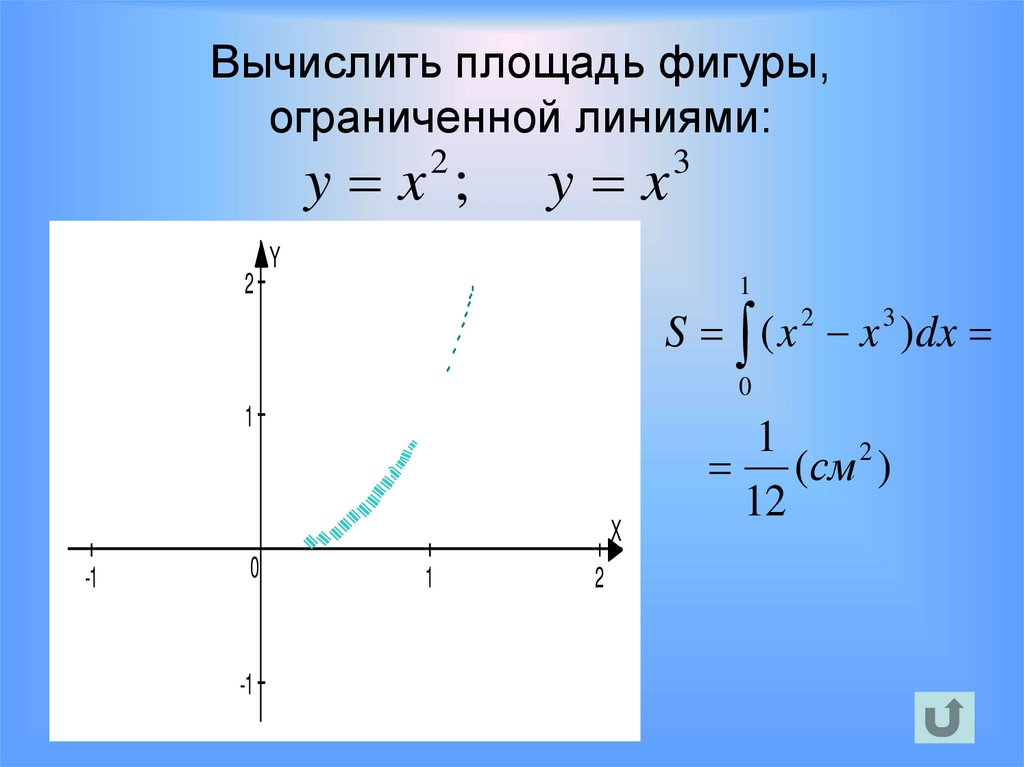
42.

Вычислить площадь фигуры,
ограниченной линиями:
y x ;
2
2
y x
3
Y
1
S ( x 2 x 3 ) dx
0
1
X
-1
0
-1
1
2
1
2
(см )
12

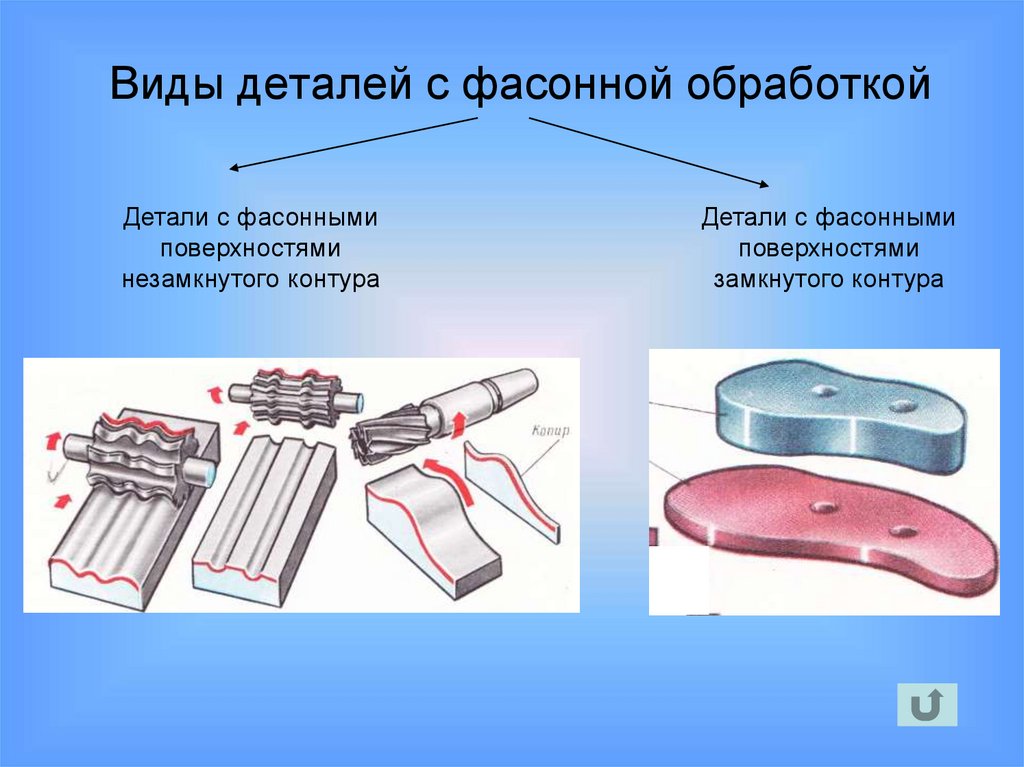
43.

• Виды деталей с фасонной обработкой
• Виды дефектов фасонных
поверхностей
• Способы обработки фасонных
поверхностей
• Схема копировального фрезерования
по замкнутому контуру
• Виды круглых поворотных столов

44.

Виды деталей с фасонной обработкой
Детали с фасонными
поверхностями
незамкнутого контура
Детали с фасонными
поверхностями
замкнутого контура

45. Виды дефектов фасонной поверхности

Вид брака
Причина
Фасонный
профиль Профиль фрезы не соответствует
детали не соответствует заданному.
заданному
При работе способом двух подач не
правильно
произведен
контроль
выпуклых
и
вогнутых
элементов
профиля.
Низкой квалификации рабочего.
Погрешность при изготовлении самого
копира.
Недостаточная чистота Неправильно приняты режимы резания.
обрабатываемой
Производится обработка на станках с
поверхности
пониженной
жесткостью
и
виброустойчивостью.

46. Способы обработки фасонных поверхностей

Фрезерование
фасонной поверхности
набором фрез
Фрезерование фасонной
поверхности с помощью
копировального
приспособления
Фрезерование
фасонной
поверхности с
помощью ручного
управления
Фрезерование
фасонной поверхности
с помощью круглого
поворотного стола

47. Способы обработки фасонных поверхностей

Фрезерование
фасонной поверхности
набором фрез
Фрезерование фасонной
поверхности с помощью
копировального
приспособления
Фрезерование
фасонной
поверхности с
помощью ручного
управления
Фрезерование
фасонной поверхности
с помощью круглого
поворотного стола

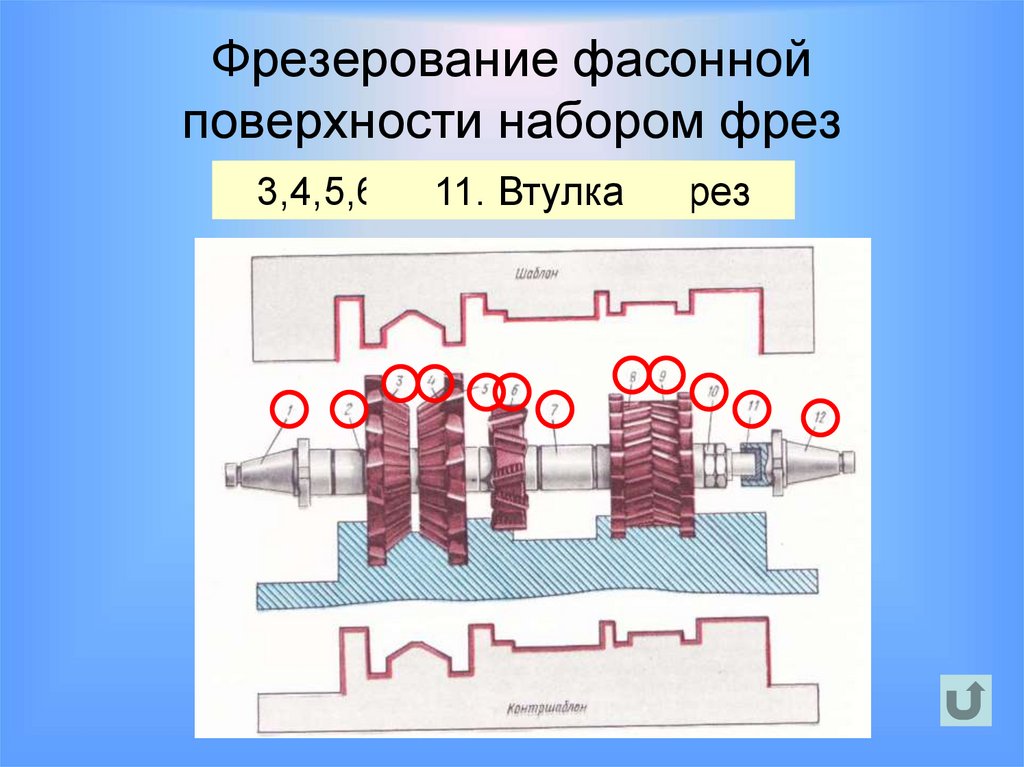
48. Фрезерование фасонной поверхности набором фрез

3,4,5,6,8,9.
2, 7.1,12.
Распорные
11.
10.
Комплект
Оправки
Втулка
Гайкивтулки
фрез

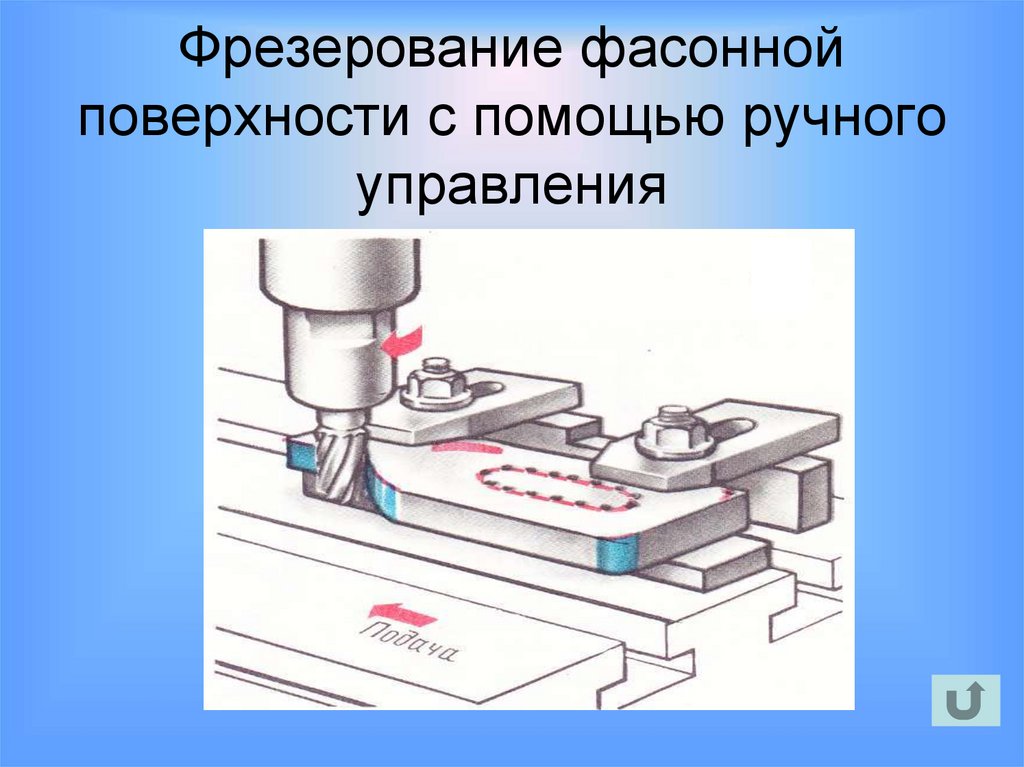
49. Фрезерование фасонной поверхности с помощью ручного управления

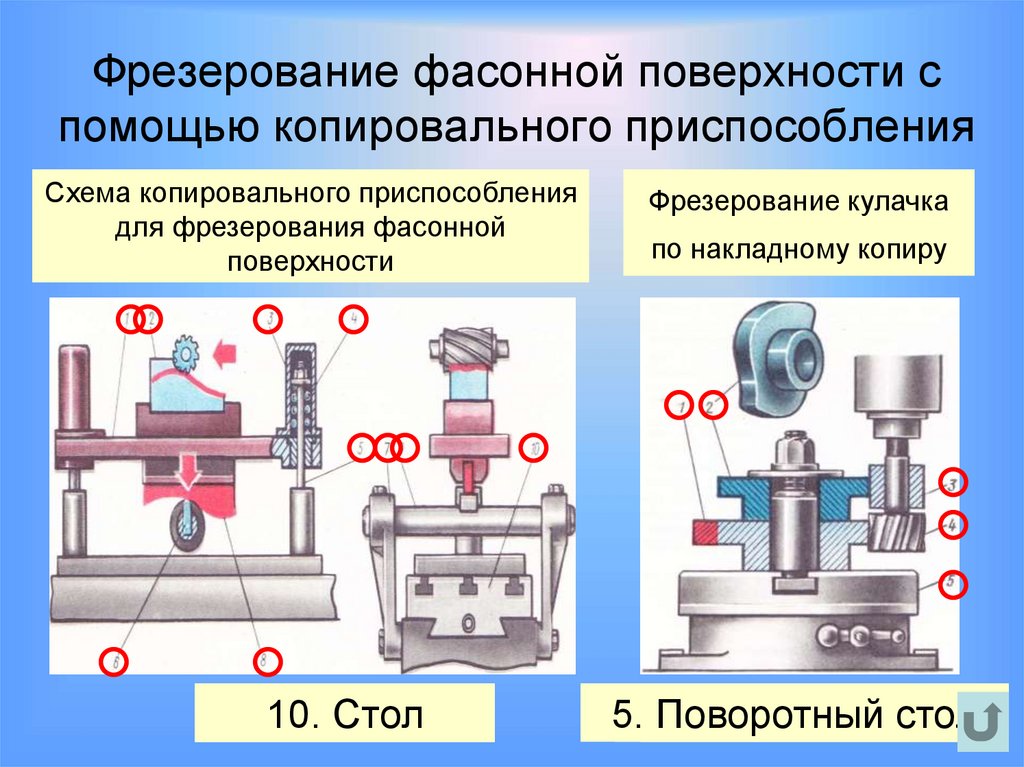
50. Фрезерование фасонной поверхности с помощью копировального приспособления

Схема копировального приспособления
для фрезерования фасонной
поверхности
7.
2.
9.
3.
4.5.
6.
Кронштейн
1.
10.
8.
Заготовка
Стержень
Колпачок
Пружина
Стойки
Палец
Плита
Копир
Стол
Фрезерование кулачка
по накладному копиру
5.4.Поворотный
Концевая
1. 2.
3.
Заготовка
Копир
Роликфреза
стол

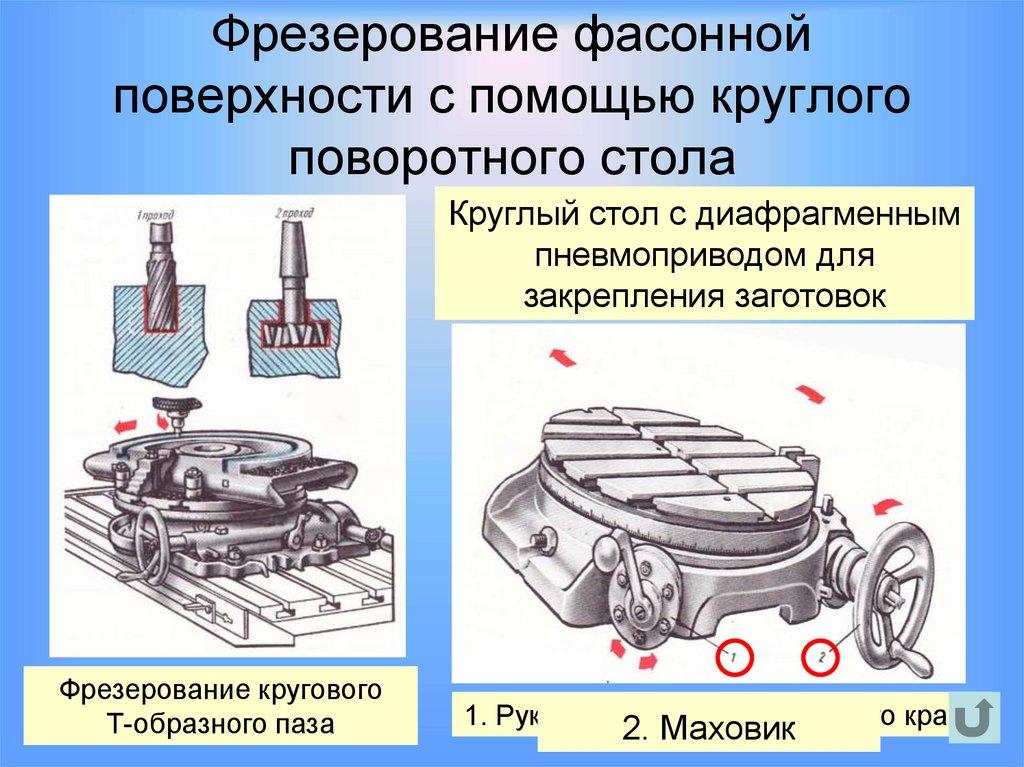
51. Фрезерование фасонной поверхности с помощью круглого поворотного стола

Круглый стол с диафрагменным
пневмоприводом для
закрепления заготовок
Фрезерование кругового
Т-образного паза
1. Рукоятка 2.
распределительного
крана
Маховик

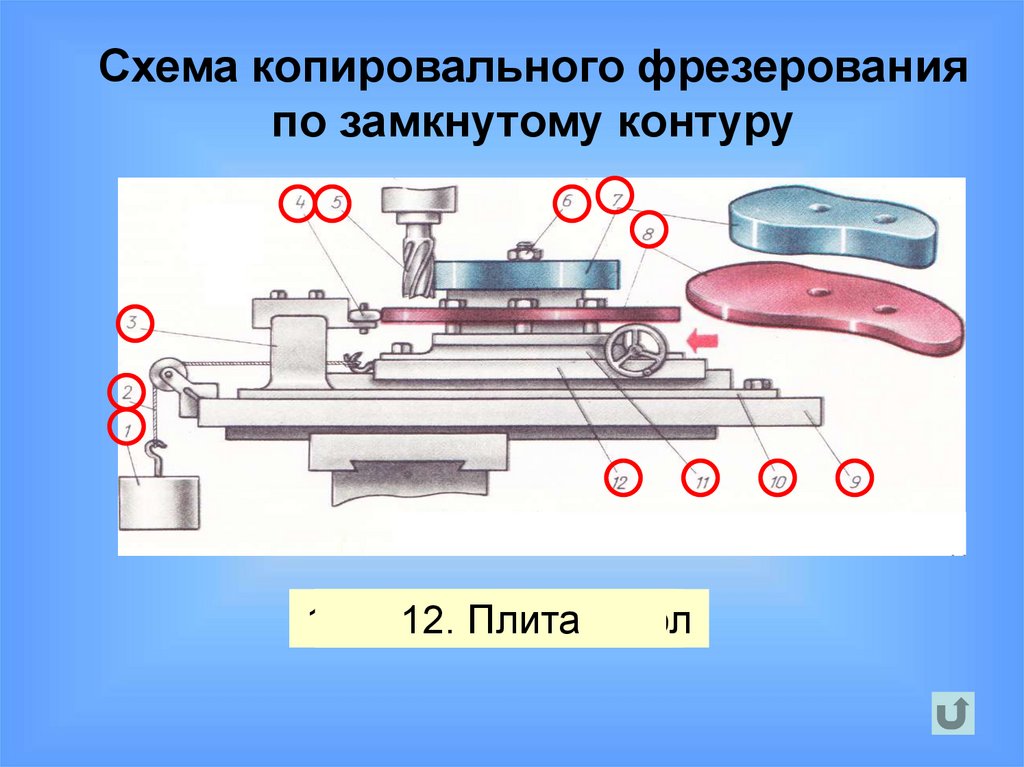
52.

Схема копировального фрезерования
по замкнутому контуру
11.6.Поворотный
7.Гайка
12.
3.
10.
5.
8.
4.
Заготовка
9.
2.
1.Стойка
Фреза
Копир
Ролик
Плита
Стол
Трос
Груз
Плита
и болт
стол

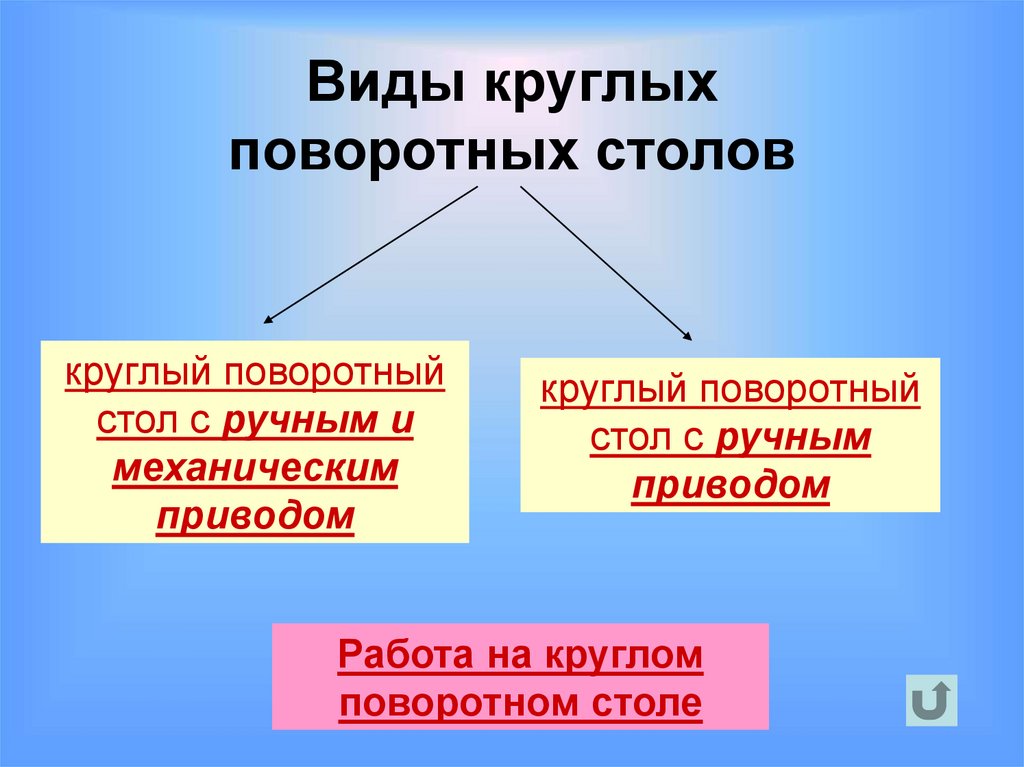
53. Виды круглых поворотных столов

круглый поворотный
стол с ручным и
механическим
приводом
круглый поворотный
стол с ручным
приводом

54. Виды круглых поворотных столов

круглый поворотный
стол с ручным и
механическим
приводом
круглый поворотный
стол с ручным
приводом
Работа на круглом
поворотном столе

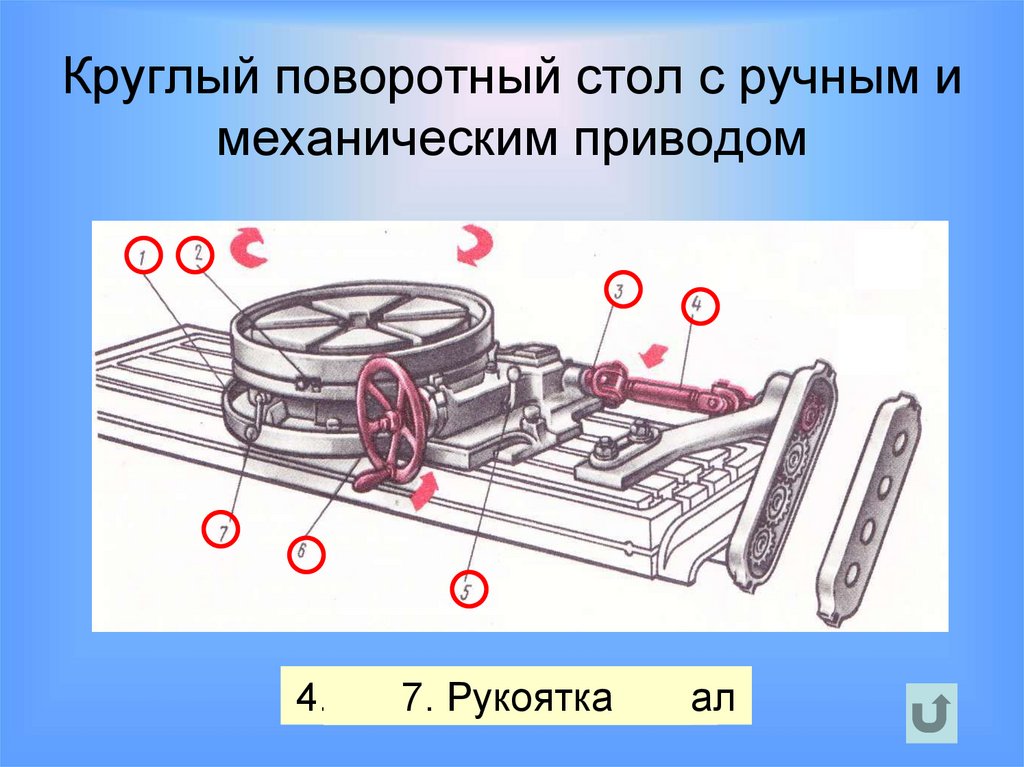
55. Круглый поворотный стол с ручным и механическим приводом

4. Телескопический
1.7.
5.Круговой
6.
3.
2.Рукоятка
Маховик
Шарнир
Кулачокпаз вал

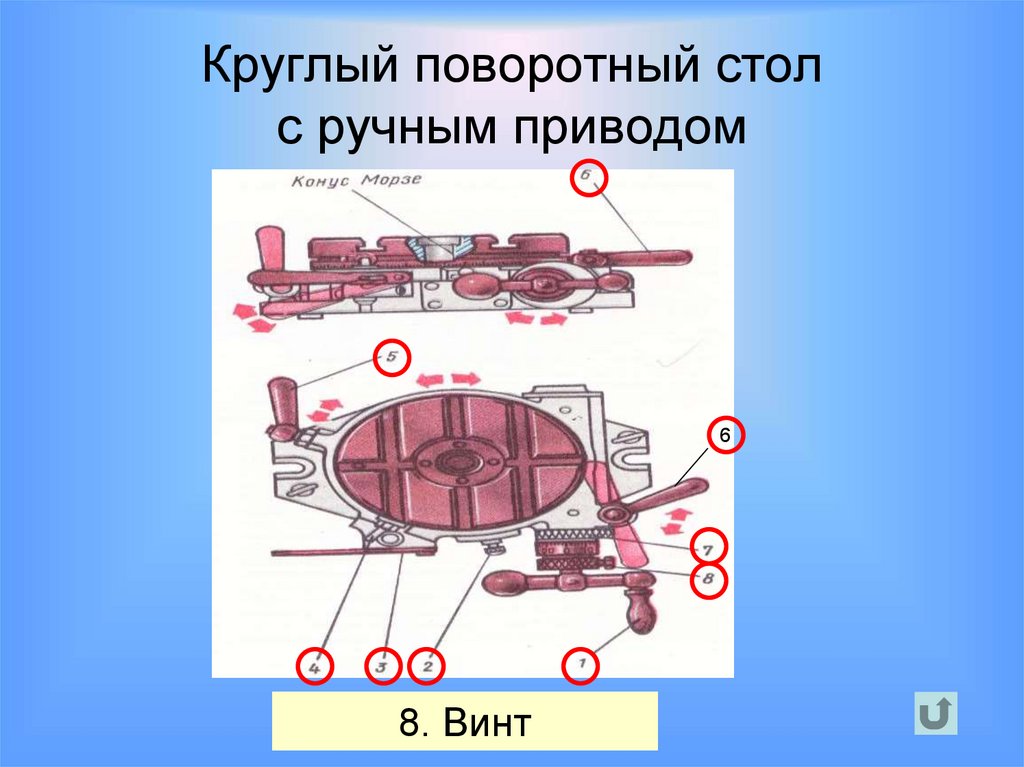
56. Круглый поворотный стол с ручным приводом

6
4. 6.
Ограничитель
1.7.8.
3.
5.
2.
Рукоятка
Рукоятка
Гильза
Винт

57. Видеофрагмент «Изготовление подставки»