Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл

1. Прикладная математика каф. МЕН

Аношина О.В.

2. Основная литература

• 1. Шипачев В. С. Высшая математика. Базовый курс: учебник и
практикум для бакалавров [Гриф Минобразования РФ] / В. С.
Шипачев; под ред. А. Н. Тихонова. - 8-е изд., перераб. и доп. Москва : Юрайт, 2015. - 447 с.
• 2. Шипачев В. С. Высшая математика. Полный курс: учебник
для акад. бакалавриата [Гриф УМО] / В. С. Шипачев; под ред. А.
Н. Тихонова. - 4-е изд., испр. и доп. - Москва : Юрайт, 2015. - 608
с
• 3. Данко П.Е., Попов А.Г., Кожевникова Т..Я. Высшая математика
в упражнениях и задачах. [Текст] / П.Е. Данко, А.Г. Попов, Т.Я.
Кожевникова. В 2 ч. – М.: Высшая школа, 2007. – 304+415c.

3. Отчетность

1.
Контрольная работа. Выполняется в соответствии:
Задания и методические указания к выполнению контрольных работ
по дисциплине «ПРИКЛАДНАЯ МАТЕМАТИКА», Екатеринбург, ФГАОУ
ВО «Российский государственный профессионально-педагогический
университет», 2016 - 30с.
Вариант контрольной работы выбирать по последней цифре номера
зачетной книжки.
2.
Экзамен

4. Неопределенный интеграл, его свойства и вычисление Первообразная и неопределенный интеграл

Определение. Функция F x называется
первообразной функции f x , определенной на
некотором промежутке, если F x f x для
каждого x из этого промежутка.
Например, функция cos x является
первообразной функции sin x , так как
cos x sin x .

5.

Очевидно, если F x - первообразная
функции f x , то F x C , где C некоторая постоянная, также является
первообразной функции f x .
Если F x есть какая-либо первообразная
функции f x , то всякая функция вида
Ф x F x C также является
первообразной функции f x и всякая
первообразная представима в таком виде.

6.

Определение. Совокупность всех
первообразных функции f x ,
определенных на некотором
промежутке, называется
неопределенным интегралом от
функции f x на этом промежутке и
обозначается f x dx .

7.

Если F x - некоторая первообразная функции
f x , то пишут f x dx F x C , хотя
правильнее бы писать f x dx F x C .
Мы по устоявшейся традиции будем писать
f x dx F x C .
Тем самым один и тот же символ
f x dx будет обозначать как всю
совокупность первообразных функции f x ,
так и любой элемент этого множества.

8. Свойства интеграла

Производная неопределенного интеграла равна
подынтегральной функции, а его дифференциалподынтегральному выражению. Действительно:
1.( f ( x)dx) ( F ( x) C ) F ( x) f ( x);
2.d f ( x)dx ( f ( x)dx) dx f ( x)dx.

9. Свойства интеграла

3. Неопределенный интеграл от
дифференциала непрерывно (x )
дифференцируемой функции равен самой
этой функции с точностью до постоянной:
d ( x) ( x)dx ( x) C,
так как (x ) является первообразной для (x).

10. Свойства интеграла

4.Если функции f1 x и f 2 x имеют
первообразные, то функция f1 x f 2 x
также имеет первообразную, причем
f1 x f 2 x dx f1 x dx f 2 x dx ;
5. Kf x dx K f x dx ;
6. f x dx f x C ;
7. f x x dx F x C .

11. Таблица неопределенных интегралов

1. dx x C .
a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x

12. Таблица неопределенных интегралов

11.
dx
arcsin x C .
1 x 2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
14.
15.
dx
a2 x2
x
arcsin C ..
a
dx
1
x a
ln
C
2
2
2a x a
x a
dx
1
a x
a 2 x 2 2a ln a x C .
dx
16.
x2 a
ln x x 2 a C .
17. shxdx chx C .
18. chxdx shx C .
19.
20.
dx
ch 2 x thx C .
dx
cthx C .
2
sh x

13. Свойства дифференциалов

При интегрировании удобно пользоваться
свойствами: 1
1. dx d (ax)
a
1
2. dx d (ax b),
a
1 2
3. xdx dx ,
2
1 3
2
4. x dx dx .
3

14. Примеры

Пример . Вычислить cos 5xdx .
Решение. В таблице интегралов найдем
cos xdx sin x C .
Преобразуем данный интеграл к табличному,
воспользовавшись тем, что d ax adx .
Тогда:
d 5 x 1
= cos 5 xd 5 x =
cos 5xdx cos 5 x
5
5
1
= sin 5 x C .
5

15. Примеры

Пример. Вычислить x
3x x 1 dx .
Решение. Так как под знаком интеграла
находится сумма четырех слагаемых, то
раскладываем интеграл на сумму четырех
интегралов:
2
3
2
3
2
3
x
3
x
x
1
dx
x
dx
3
x
dx xdx dx .
x3
x4 x2
3
x C
3
4
2

16. Независимость от вида переменной

При вычислении интегралов удобно
пользоваться следующими свойствами
интегралов:
Если f x dx F x C , то
f x b dx F x b C .
Если f x dx F x C , то
1
f ax b dx F ax b C .
a

17. Пример

Вычислим
1
6
(
2
3
x
)
dx
(
2
3
x
)
C
.
3 6
5

18. Методы интегрирования Интегрирование по частям

Этот метод основан на формуле udv uv vdu .
Методом интегрирования по частям берут такие интегралы:
а) x n sin xdx , где n 1,2...k ;
б) x n e x dx , где n 1,2...k ;
в) x n arctgxdx , где n 0, 1, 2,... k . ;
г) x n ln xdx , где n 0, 1, 2,... k .
При вычислении интегралов а) и б) вводят
n 1
обозначения: x n u , тогда du nx dx , а, например
sin xdx dv ,тогда v cos x .
При вычислении интегралов в), г) обозначают за u функцию
arctgx , ln x , а за dv берут x n dx .

19. Примеры

Пример. Вычислить x cos xdx .
Решение.
u x, du dx
=
x cos xdx
dv cos xdx, v sin x
x sin x sin xdx x sin x cos x C .

20. Примеры

Пример. Вычислить
x ln xdx
dx
u ln x, du
x
x2
dv xdx, v
2
x2
x 2 dx
ln x
=
2
2 x
x2
1
x2
1 x2
ln x xdx
ln x
C .
=
2
2
2
2 2

21. Метод замены переменной

Пусть требуется найти f x dx , причем
непосредственно подобрать первообразную
для f x мы не можем, но нам известно, что
она существует. Часто удается найти
первообразную, введя новую переменную,
по формуле
f x dx f t t dt , где x t , а t - новая
переменная

22. Интегрирование функций, содержащих квадратный трехчлен

Рассмотрим интеграл
ax b
dx ,
x px q
содержащий квадратный трехчлен в
знаменателе подынтегрального
выражения. Такой интеграл берут также
методом замены переменных,
предварительно выделив в
знаменателе полный квадрат.
2

23. Пример

Вычислить
dx
.
x 4x 5
Решение. Преобразуем x 2 4 x 5 ,
2
выделяя полный квадрат по формуле a b 2 a 2 2ab b 2 .
Тогда получаем :
x2 4x 5 x2 2 x 2 4 4 5
x 2 2 2 x 4 1 x 2 2 1
x 2 t
dx
dx
dt
x t 2
2
2
2
x 2 1 dx dt
x 4x 5
t 1
arctgt C arctg x 2 C.

24. Пример

Найти
1 x
1 x
2
dx
tdt
1 t
2
x t, x t 2 ,
dx 2tdt
2
t2
1 t
2
dt
1 t
1 t
d (t 2 1)
t
2
1
2
2tdt
2
dt
ln(t 1) 2 dt 2
2
1 t
ln(t 2 1) 2t 2arctgt C
2
ln( x 1) 2 x 2arctg x C.
1 t 2 1
1 t
2
dt

25. Определенный интеграл, его основные свойства. Формула Ньютона- Лейбница. Приложения определенного интеграла.

• К понятию определенного интеграла приводит
задача нахождения площади криволинейной
трапеции.
• Пусть на некотором интервале [a,b] задана
непрерывная функция y f ( x ) 0
Задача:
Построить ее график и найти F площадь фигуры,
ограниченной этой кривой, двумя прямыми x = a и x
= b, а снизу – отрезком оси абсцисс между точками
x = a и x = b.

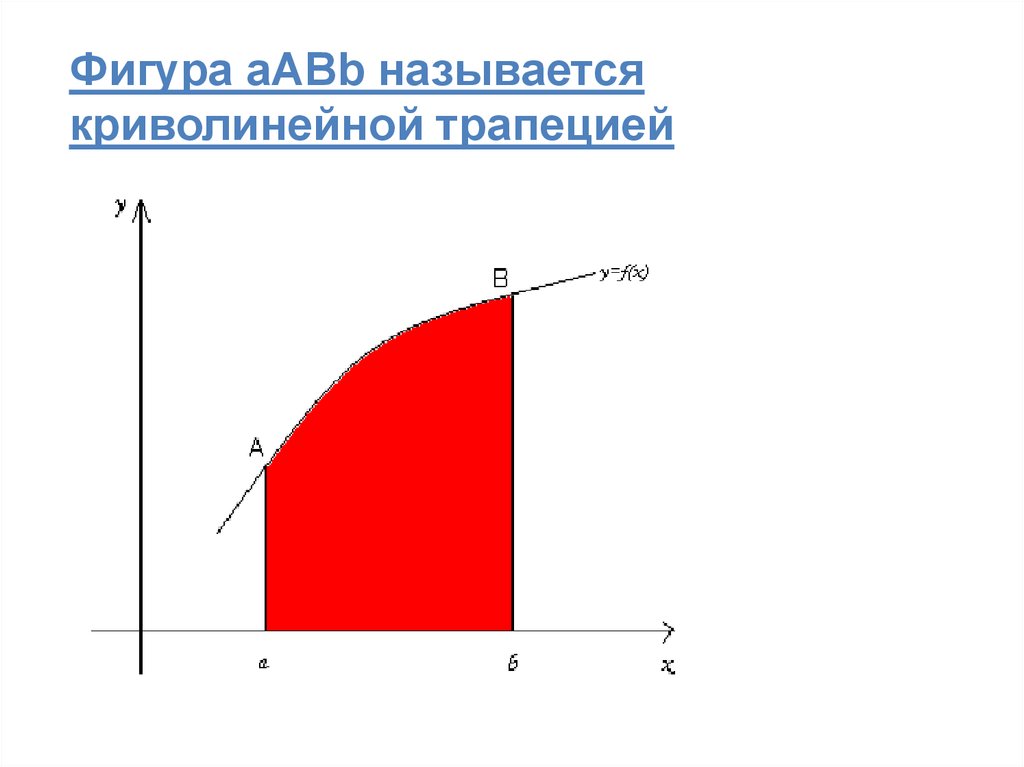
26.

Фигура aABb называется
криволинейной трапецией

27. Определение

b
f ( x)dx
Под определенным интегралом
a
от данной непрерывной функции f(x) на
данном отрезке [a;b] понимается
соответствующее приращение ее
первообразной, то есть
F (b) F (a ) F ( x) /
b
a
Числа a и b – пределы интегрирования, [a;b]
– промежуток интегрирования.

28. Правило:

• Определенный интеграл равен разности
значений первообразной подынтегральной
функции для верхнего и нижнего пределов
интегрирования.
• Введя обозначения для разности
b
F (b) F (a) F ( x) / a
b
f ( x)dx F (b) F (a)
a
Формула Ньютона – Лейбница.

29. Основные свойства определенного интеграла.

1)Величина определенного интеграла не зависит от
обозначения переменной интегрирования, т.е.
b
b
a
a
f ( x)dx f (t )dt
где x и t – любые буквы.
2)Определенный интеграл с одинаковыми
пределами
интегрирования равен нулю
a
f ( x)dx F (a) F (a) 0
a

30.

3) При перестановке пределов интегрирования
определенный интеграл меняет свой знак на обратный
b
a
f ( x)dx F (b) F (a) F (a) F (b) f ( x)dx
a
b
(свойство аддитивности)
4) Если промежуток [a;b] разбит на конечное число
частичных промежутков, то определенный интеграл,
взятый по промежутку [a;b], равен сумме определенных
интегралов, взятых по всем его частичным промежуткам.
b
c
b
f ( x)dx f ( x)dx
c
a
a
f ( x)dx

31.

5)Постоянный множитель можно выносить
за знак определенного интеграла.
6)Определенный интеграл от алгебраической
суммы конечного числа непрерывных
функций равен такой же алгебраической
сумме определенных интегралов от этих
функций.

32. 3. Замена переменной в определенном интеграле.

3. Замена переменной в определенном
интеграле.
b
f ( x)dx f (t ) (t )dt
a
a ( ), b ( ), (t ) [a; b]
где
для t [ ; ] , функции (t ) и (t ) непрерывны на ;
5
Пример:
1
=
x 1dx
=
x 1 5
t 0 4
x 1 t
dt dx
4
0
3
2
t dt t 2
3
4
0
2
2
16
1
t t 40 4 2 0
5
3
3
3
3

33.  Несобственные интегралы.

Несобственные интегралы.
Определение. Пусть функция f(x) определена на
бесконечном интервале [a; + ) и интегрируется
на любом интервале [a;b], где b < + . Если
существует
b
lim
f ( x)dx,
b
a
то этот предел называется несобственным
интегралом функции f(x) на интервале
[a; + ) и обозначается
f ( x.)dx
a

34.

• Таким образом, по определению,
b
f ( x)dx lim f ( x)dx lim ( F (b) F (a))
a
b
a
b
Если этот
предел некоторое
число, то
интеграл
f ( x)dx
a
называется
сходящимся, если предела не существует, или он равен ,
то говорят, что интеграл расходится.

35. Пример. Интеграл Пуассона:

e
x2
a2
dx
• если а = 1, то
e
x2
dx
• Интеграл сходится, и его значение
.

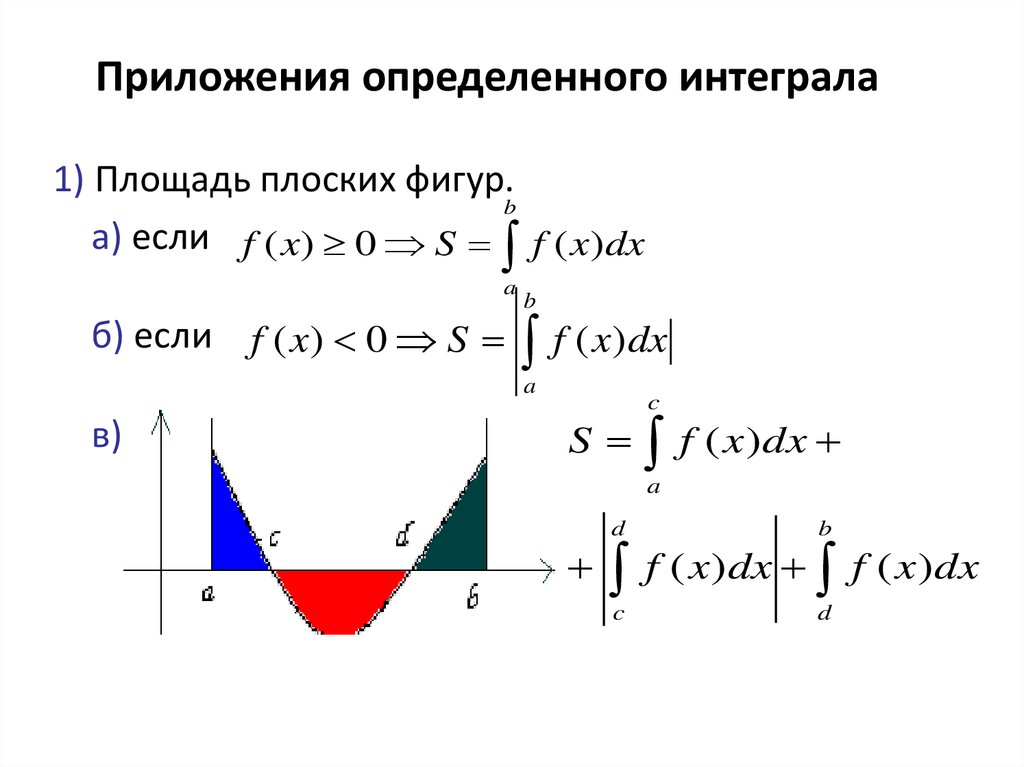
36. 5. Приложения определенного интеграла

1) Площадь плоских фигур.
b
а) если f ( x) 0 S f ( x)dx
a
б) если f ( x) 0 S
b
f ( x)dx
a
в)
c
S
f ( x)dx
a
d
b
c
d
f ( x)dx f ( x)dx

37.

b
г) S f ( x) ( x) dx
a
2) Многие физические величины можно
определить и задать через понятие
интеграла. Например, работа для любой
силы вычисляется как интеграл от величины
b
силы по длине пути.
A F ( x)dx
a

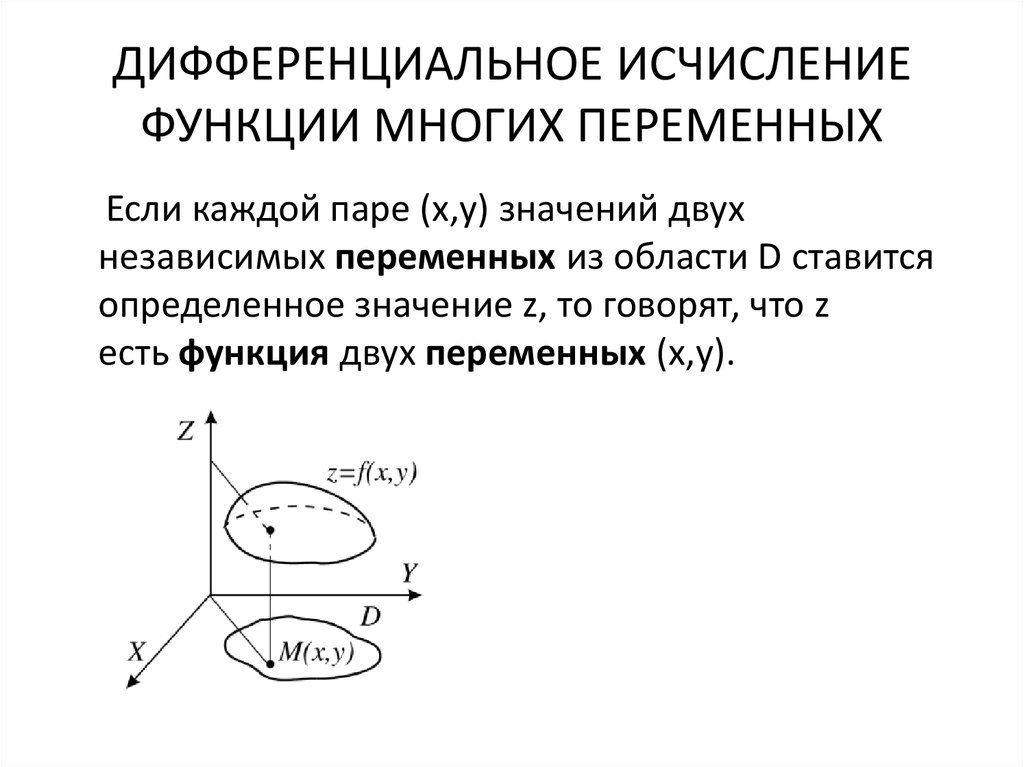
38. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ

Если каждой паре (x,y) значений двух
независимых переменных из области D ставится
определенное значение z, то говорят, что z
есть функция двух переменных (x,y).

39. Частные приращения и частные производные

x z f ( x x, y ) f ( x, y )
xz
lim
x 0 x
z
f ( x, y )
; z x ;
;
x
x
f x ( x, y ).
y z f ( x, y y) f ( x, y)
lim
y 0
yz
y
z
f ( x, y)
; z y ;
;
y
y
f y ( x, y).

40. Полное приращение функции 2-х переменных

Если обеим переменным дать
приращение, то функция получит
полное приращение
z f ( x x, y y ) f ( x, y )

41. Полное приращение и полный дифференциал

z f ( x x, y y) f ( x, y)
dz f x ( x, y)dx f y ( x, y)dy
z
z
dz dx dy
x
y
u
u
u
du
dx dy dz
x
y
z

42. Дифференциалы высшего порядка

Дифференциалом второго порядка
функции z=f(x,y) называется
d 2 z d (dz )
n 1
Вообще: d z d (d z )
Если х и у независимые переменные, то
2
2
2
.
d z z dx 2z dxdy z dy
n
xx
xy
yy

43. Экстремумы функции двух переменных

Определение. Говорят, что в точке P0 ( x0 , y0 )
функция f (x,y) имеет максимум, если cуществует
такая окрестность этой точки, что для всех точек
P(x,y) этой окрестности, отличных от P0 ( x0 , y0 ) ,
выполнено неравенство
f ( P0 ) f ( P).
Аналогично определяется минимум функции.
Минимум и максимум функции называются ее
экстремумами.

44. Экстремумы функции двух переменных

Теорема (необходимое условие
экстремума). В точке экстремума функции
нескольких переменных каждая ее частная
производная либо равна нулю, либо не
существует.
Точки, в которых выполнены эти условия,
называются критическими.

45. Достаточные условия экстремума функции двух переменных

Теорема. Пусть функция z=f(x,y) определена и имеет непрерывные
частные производные до 3-го порядка в некоторой окрестности точки
M 0 ( x0 , y 0 )
, в которой z x z y 0 . Если при этом в этой точке
выполнено условие
z xx z yy ( z xy ) 2 0
, то точка M 0
является точкой экстремума функции, причем точкой максимума, если
z xx 0
, и точкой минимума, если
Если же в этой точке
z xx 0
.
z xx z yy ( z xy ) 2 0 , то
экстремума в точке
M 0 нет.
В том случае, если z xx z yy ( z xy ) 0 в точке M 0 , теорема ответа
2
не дает.

46. Пример

Исследовать на экстремум функцию
50 20
z xy , åñëè x 0 u y 0.
x
y

47. Наибольшее и наименьшее значения функции

Определение. Наименьшее или наибольшее
значение функции в данной области
называется абсолютным экстремумом
функции (абсолютным минимумом или
абсолютным максимумом соответственно)
в этой области.

48.

Известно, что непрерывная в
замкнутой ограниченной области
функция достигает в ней своих
наибольшего и наименьшего
значений.
Абсолютный экстремум достигается
функцией либо в критических точках,
либо на границе области.

49.

Пусть функция непрерывна в замкнутой
ограниченной области G, дифференцируема внутри
этой области. Чтобы найти наибольшее и
наименьшее значения функции в этой области,
нужно:
1)найти критические точки, принадлежащие этой
области, и вычислить в них значения функции;
2)найти наибольшее и наименьшее значения функции
на границе области;
3)из всех найденных значений выбрать наибольшее и
наименьшее.

50. Скалярное поле Основные определения

Пусть в области D пространства Охуz
задана функция u=u(х,у,z). В этом случае
говорят, что в области D задано скалярное
поле, а саму функцию u=u(х,у,z)называют
функцией поля. Например, поле давлений,
температур и т.д.

51. Скалярное поле Основные определения

Множество точек М области D, для которых
скалярное поле сохраняет постоянное
значение, т. е. u(М)=С, называется
поверхностью уровня ( или
изоповерхностью) скалярного поля.

52.

Если область D расположена на плоскости
Оху, то поле u=u(х,у) является плоским.
Поверхности уровня называют в этом
случае линиями уровня.

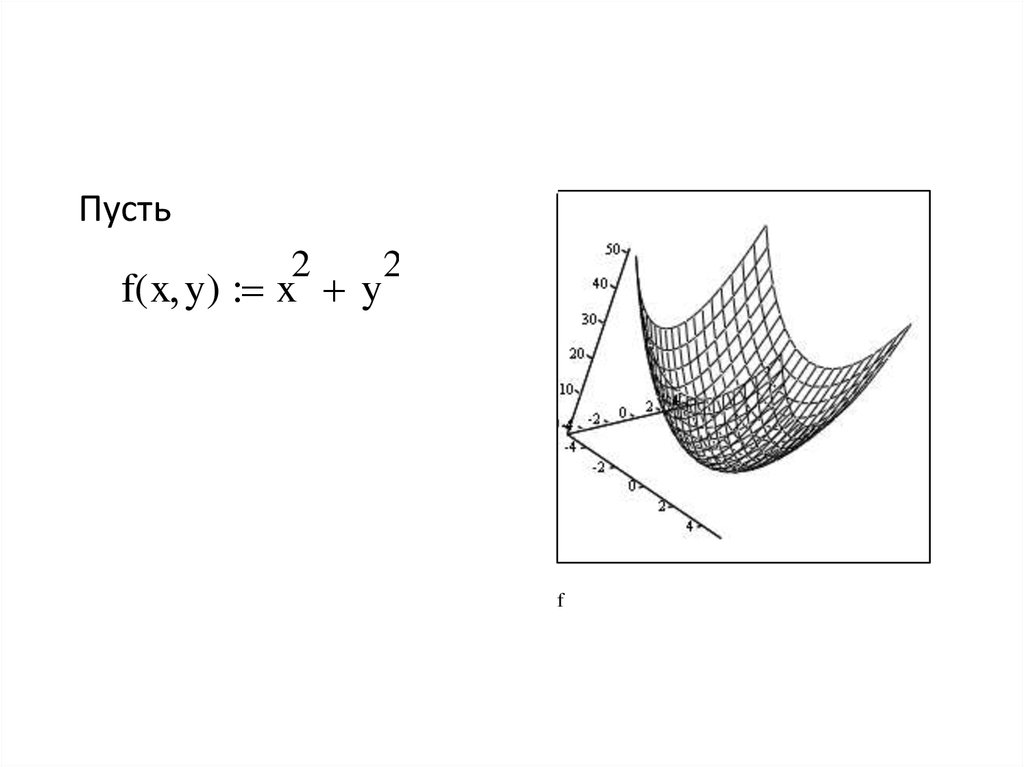
53.

Пусть
2
f( x y) x y
2
f

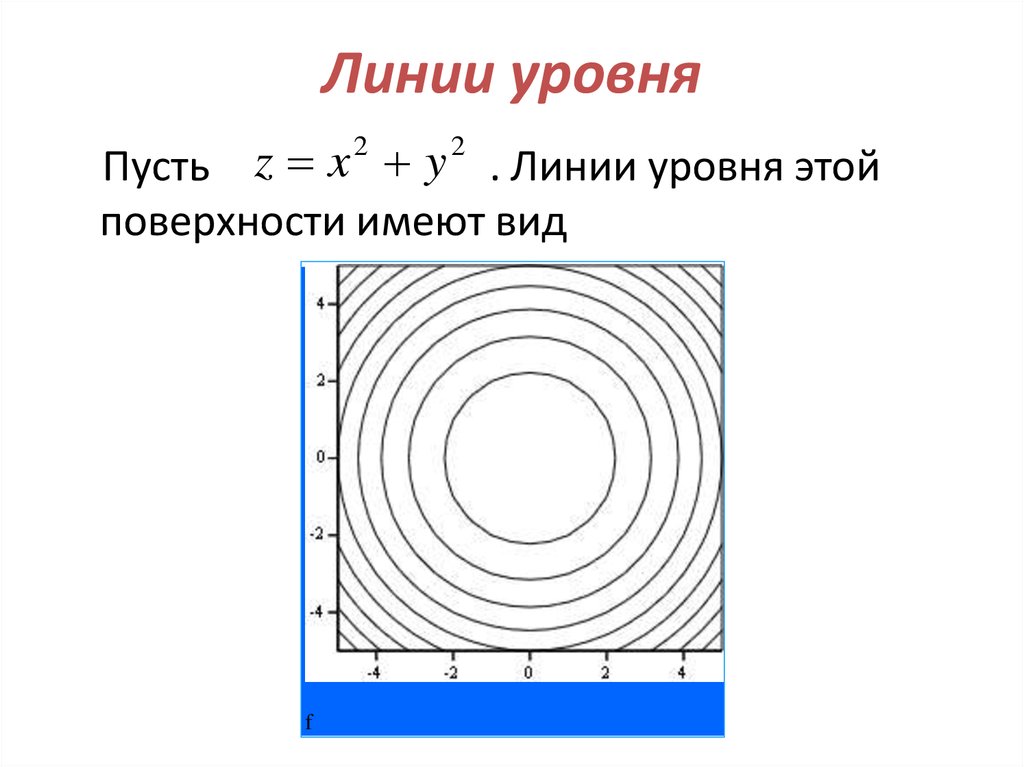
54. Линии уровня

Пусть z x y . Линии уровня этой
поверхности имеют вид
2
f
2

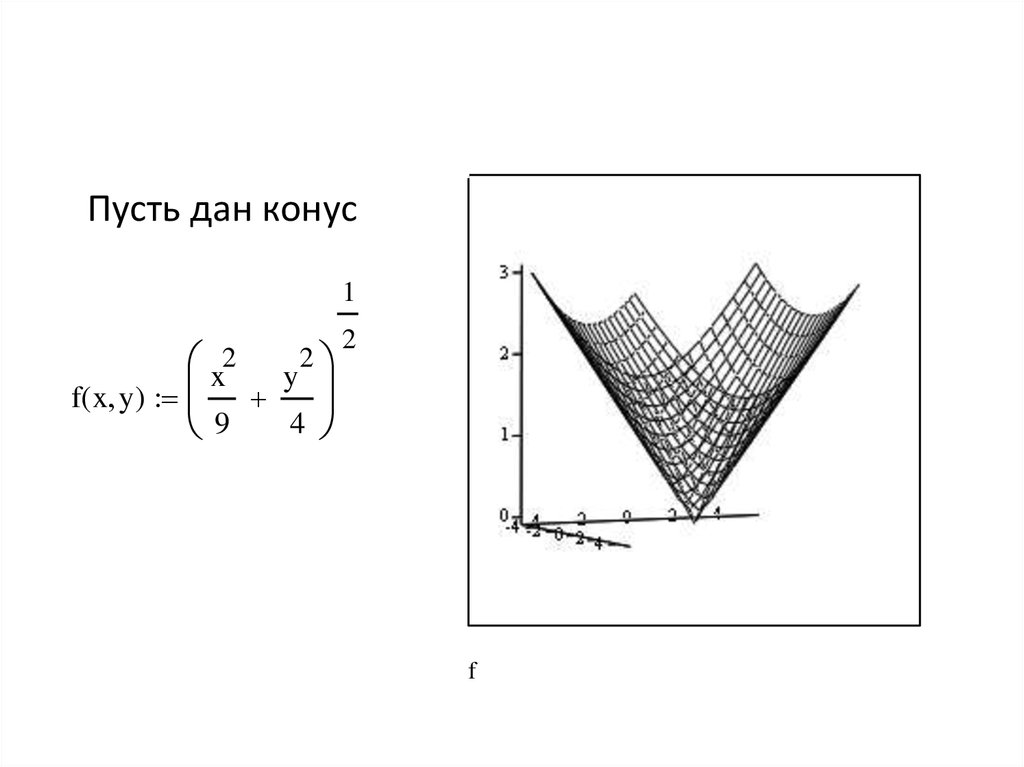
55.

Пусть дан конус
1
x
y
f( x y )
4
9
2
2
2
f

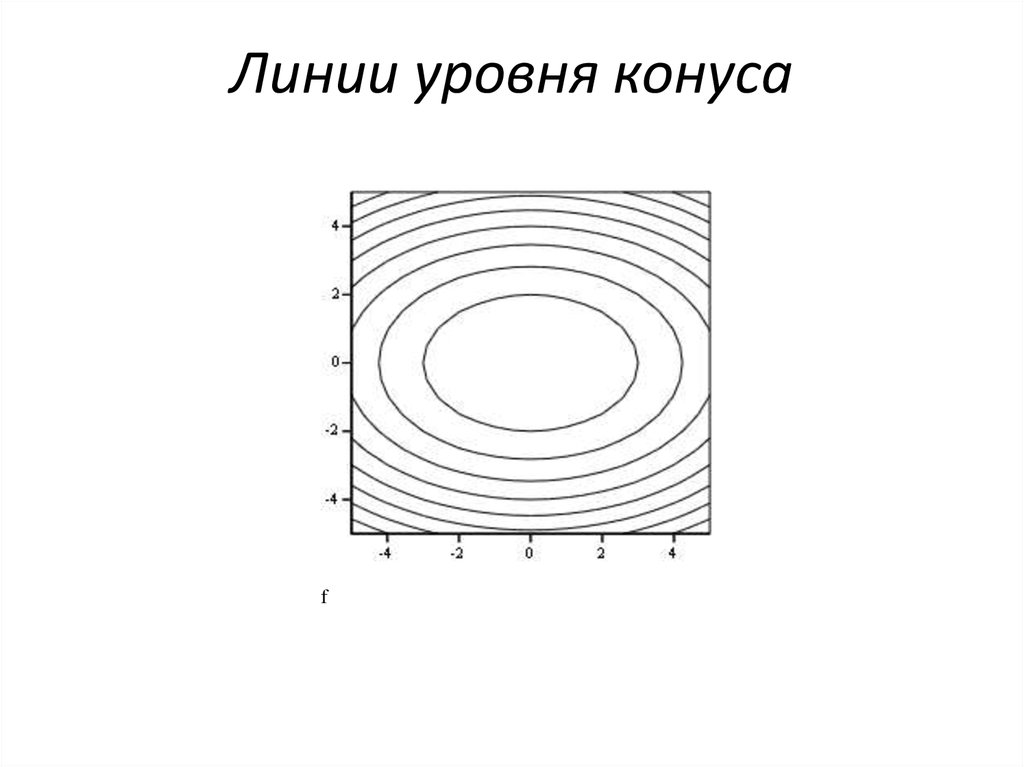
56. Линии уровня конуса

f

57.

Пусть задана дифференцируемая функция
скалярного поля. u u x, y, z
Рассмотрим точку P x, y, z этого поля и луч
, выходящий из точки P в направлении
единичного вектора
0 cos α; cos β; cos γ ,
где
0
α, β, γ –углы, образованные вектором
с осями координат .

58. Определение

z
P1
γ
ℓ
β
P
α
0
x
x
y
Рис.
Пусть P1 x x , y y , z – z
какая-нибудь другая точка
этого луча. Обозначим
PP1 x 2 y 2 z 2
– расстояние между точками
P и Ρ1 ; называют
величиной перемещения.
Приращением функции в
направлении назовем
разность
u u Ρ1 u Ρ

59.

Производной функции u u x, y, z
в точке P по направлению называется
предел отношения приращения функции в
направлении
к величине перемещения при 0 :
u
u
lim
0 .

60. Вычисление производной по направлению

Формула вычисления производной по
направлению:
u u
u
u
cos cos cos , ãäå
x
y
z
ly
lx
lz
cos , cos , cos ,
l
l
l
l lx2 l y2 lz2 .

61. Градиент скалярного поля

Градиентом скалярного поля u=u(x,y,z), где
u=u(x,y,z)-дифференцируемая функция,
называется вектор с координатами
u u u .
, ,
x y z
Таким образом,
u u u
gradu ( , , )
x y z
или
.
u
u
u
gradu
x
i
y
j
z
k

62. Пример

2
2
Найти градиент функции u= x y z
M(6,2,3).
Решение. Вычислим градиент функции.
u
x
x
u
z
Тогда grad u =
А в точке М
в точке
y
u
y
x2 y 2 z 2
2
x2 y 2 z 2
z
x2 y 2 z 2
x
x2 y2 z 2
i+
y
x2 y2 z 2
j +
6 2
3
gradu i j k .
7 7
7
z
x2 y2 z 2
k

63. Направление градиента

Теорема. Производная функции по
направлению ul равна проекции
градиента этой функции на данное
направление (в соответствующей
точке).

64. Направление градиента

Так как производная по направлению
представляет собой скорость изменения функции
в данном направлении , а проекция вектора на
другой вектор имеет максимальное значение,
если оба вектора совпадают по направлению, то
градиент функции в данной точке указывает
направление наиболее быстрого возрастания
функции.

65. Величина градиента плоского скалярного поля

Величина градиента плоского скалярного
поля ,т.е.
2
2
u u
grad u =
x y
обозначается tg и определяет крутизну
наибольшего ската или подъема
поверхности u = f (x, y).

66.

Градиент скалярного поля в данной точке по
величине и направлению равен
максимальной скорости изменения поля в
этой точке, т. е.
u u
,
max
gradu
l
где
l
l *
.
l gradu
*

67. Обыкновенные дифференциальные уравнения

Обыкновенным
дифференциальным
уравнением
называется уравнение, связывающее между собой
значения независимой переменной x, неизвестной
функции y = f(x) и её производных (или
дифференциалов):
Порядком уравнения называется максимальный порядок n
входящей в него производной (или дифференциала).
Функция y(x) называется решением (или интегралом)
дифференциального уравнения если при подстановке ее в
уравнение обращает его в тождество.
Пример: y(4) – y + x = 0 - уравнение четвёртого порядка.

68.

ОДУ первого порядка
Обыкновенным дифференциальным уравнением
первого порядка называется уравнение вида:
где x - независимая переменная, y(x) - неизвестная функция
Общее решение:
Пример:
y ( x) 3 x 0
общее решение:
y ( x)
3 2
x c
2

69.

Разделяют несколько типов (видов) обыкновенных
дифференциальных уравнений:
-Уравнения с разделяющимися переменными,
-Однородные уравнения,
-Линейные уравнения,
-Уравнение в полных дифференциалах,
-и т.д.
Остановимся подробнее на каждом из этих типов
уравнений.

70.

Уравнения с разделёнными переменными.
Так называются уравнения вида удовлетворяющее
начальному условию
f(x)dx + g(y)dy = 0,
Интегрируя, получим
- общий интеграл (общее решение) этого
уравнения.
Пример:
e y dy ( x3 7 x) dx 0;
x4 7 2
e
x c 0
4 2
y
e y dy ( x 3 7 x) dx 0;
- общее решение

71.

Уравнения с разделяющимися переменными.
Так называются уравнения вида
Эти уравнения легко сводятся к уравнению с разделёнными
переменными:
Записываем уравнение в форме:
затем делим на g(y) и умножаем на dx:
.
Это уравнение - с разделёнными переменными. Интегрируя,
получим общий интеграл:

72.

Пример:
Выразим у из последнего выражения как функцию х, получим
общее решение:

73.

Уравнения с однородной правой частью. Так называются уравнения со
специальным видом зависимости функции f(x, y) от своих аргументов:
Это уравнение сводится к уравнению с разделяющимися переменными
относительно новой неизвестной функции u(x) заменой:
Подставляя в уравнение y = x·u, y ′ = u + x·u ′, получим
(это - уравнение с разделяющимися переменными),
- это общий интеграл уравнения относительно переменных x, u

74.

Пример:
- общее решение уравнения

75.

Пример:
Окончательно, получим общее решение:

76.

Линейные уравнения. ДУ первого порядка называется линейным,
если неизвестная функция y(x) и её производная входят в уравнение
в первой степени:
здесь p(x), q(x) - непрерывные функции.
Пример:
dy
sin( x) y ctg ( x);
dx
y (1 x 2 ) y 37 x 5.

77.

Для решения уравнения представим y(x) в виде произведения двух новых
неизвестных функций u(x) и v(x): y(x) = u(x)v(x).
Тогда
и уравнение приводится к виду:
или
Это уравнение решаем в два этапа: сначала находим функцию v(x) как
частное решение уравнения с разделяющимися переменными:
затем находим u(x) из уравнения:

78.

Отметим, решая уравнение на v(x) мы не вводим в это решение
произвольную постоянную C, нам достаточно найти одну функцию v(x),
обнуляющую слагаемое со скобками.
Запоминать эту формулу не
надо, лучше усвоить порядок действий и воспроизводить его при решении
каждой задачи.

79.

Пример:
Решение:
и общее решение уравнения
.

80.

Для нахождения частного решения, соответствующего
начальным условиям (задача Коши), подставим в общее
решение
Решение задачи:

81.

Уравнение в полных дифференциалах. Так называется уравнение вида
P(x, y) dx + Q(x, y) dy = 0.
(P(x, y), Q(x, y) - непрерывно дифференцируемы) в случае, если его левая
часть является полным дифференциалом некоторой функции u(x, y), т.е.
если существует такая функция u(x, y), что
Необходимым и достаточным условием существования такой функции
является условие:
Если - уравнение в полных дифференциалах, то его правая часть равна 0,
т.е. принимает вид du(x, y) = 0. На решении y(x) получим du(x, y(x)) = 0,
следовательно, u(x,y(x)) = C, где C - произвольная постоянная.
Соотношение u(x, y) = C и есть общее решение уравнения в полных
дифференциалах.

82.

Для нахождения функции u(x, y) решается система уравнений
Из первого уравнения этой системы находим:
с точностью до произвольной дифференцируемой по y
функции
(эта функция играет роль постоянной интегрирования;
так как интегрирование ведётся по переменной x.
Дифференцируем эту функцию по y и приравниваем выражению,
стоящему во втором уравнении системы (т.е.
), получим
дифференциальное уравнение из которого можно найти
.

83.

Пример: найти общее решение уравнения
Убедимся, что это - уравнение в полных дифференциалах.
.

84.

ОДУ высших порядков
Обыкновенным дифференциальным уравнением называется
уравнение, связывающее между собой значения независимой
переменной x, неизвестной функции y = f(x) и её производных
(или дифференциалов):
Общим решением (общим интегралом) уравнения называется
соотношение вида:

85.

Некоторые типы уравнений, допускающие понижение порядка.
Уравнение вида
решается последовательным n-кратным интегрированием.
Пример:
Переобозначив постояные, общее решение запишем в виде :
y = cos x + C1x3 + C2x2 + C3x + C4.

86.

Уравнение, не содержащее в явном виде неизвестную функцию и её
младшие производные.
Порядок уравнения вида F(x, y(k), y(k+1), y(k+2), …,y(n)) = 0, не содержащего
функции y(x) и (k – 1) младшую производную этой функции в явном виде,
может быть понижен ровно на k единиц введением новой неизвестной
функции
z(x) = y(k)(x). Тогда уравнение примет вид
т.е. будет уравнением (n – k)-го порядка.
После нахождения z(x) последовательным интегрированием решается
уравнение y(k)(x)= z(x).

87.

Пример: Понизить порядок уравнения:
Младшая производная, входящая в явной форме в уравнения, - вторая,
поэтому делаем замену искомой функции:
Тогда:
и уравнение примет вид

88.

Уравнение, не содержащее в явном виде независимую переменную x.
Порядок уравнения
не содержащего явно x, может быть понижен на 1 с помощью приёма,
который заключается в том, что вводится новая функциональная
зависимость от y:
Пример: Понизить порядок уравнения:
Переменная x явно в уравнение не входит, поэтому полагаем
тогда
.
Просто сократить на p это уравнение нельзя, так как можно потерять
семейство решений
поэтому рассматриваем два случая:
,

89. Спасибо за внимание!