Конструктивная логика(1)

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Неклассические логики»
Тема «Конструктивные логики»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2014

2. Л.Э.Я. БРАУЭР

• В 1908 г. голландский аспирант
Л.Э.Я. Брауэр опубликовал
диссертацию под названием «De
onbetrouwbaarheid der logische
principes», что означает
«Недостоверность логических
принципов».
•Брауэр аргументировал, что
причина неприятностей в
математике начала XX века в
самой логике.
Курс «Неклассические логики»
Тема «Конструктивные логики»
2

3. ЗАКОН ИСКЛЮЧЕННОГО ТРЕТЬЕГО

А ∨ ¬А
• Для бесконечных объектов
закон исключенного третьего
«или не» не выполняется
автоматически.
• Он в обычной логике
эквивалентен еще одному
общепринятому закону: закону
снятия двойного отрицания.
Курс «Неклассические логики»
Тема «Конструктивные логики»
3

4. ЗАКОН ДВОЙНОГО ОТРИЦАНИЯ

• Закон двойного отрицания в
¬ ¬ А ⇔ А курсе математики выступает
в качестве доказательств от
противного: «Нужно
доказать А. Предположим,
что не верно А… Получаем
абсурд. Полученное
противоречие доказывает
теорему».
Курс «Неклассические логики»
Тема «Конструктивные логики»
4

5. КОНСТРУКТИВНАЯ ЛОГИКА

• Конструктивная логика – раздел
математической логики, изучающий
рассуждения о конструктивных объектах и
конструкциях.
• Самое заметное отличие от традиционной
логики состоит в отсутствии закона
исключенного третьего и закона двойного
отрицания.
А ∨ ¬А
¬¬А⇔А
Курс «Неклассические логики»
Тема «Конструктивные логики»
5

6. КОНСТРУКТИВНАЯ АРИФМЕТИКА

• Конструктивная арифметика –
гейтинговская арифметика, или ее
расширение, получаемое добавлением
принципа Маркова и схемы:
А↔∃e(e r A)
• Эта схема выражает эквивалентность
формулы и утверждения о ее
реализуемости.
Курс «Неклассические логики»
Тема «Конструктивные логики»
6

7. КОНСТРУКТИВНАЯ АРИФМЕТИКА

• Конструктивная арифметика не является
подсистемой классической арифметики: в
ней опровергается закон исключенного
третьего:
∀x (A(x) ∨ ¬A(x))
• Эта расширенная система достаточна для
доказательства основных результатов
конструктивного математического анализа.
Курс «Неклассические логики»
Тема «Конструктивные логики»
7

8. СИСТЕМЫ КОНСТРУКТИВНОЙ ЛОГИКИ

• Общая черта большинства систем – явная
реализация связки ∨ и квантора ∃:
выводимость A ∨ B. При этом в случае
прикладных систем требуется замкнутость
рассматриваемых формул.
• Большинство систем корректны относительно
различных понятий реализуемости.
• Формальные системы обычно неполны
относительно естественной конструктивной
семантики.
Курс «Неклассические логики»
Тема «Конструктивные логики»
8

9. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ

• Конструктивное исчисление высказываний
неполно относительно реализуемости, но полно
при некоторой интерпретации в терминах
систем Поста.
• Арифметическая полуформальная система,
полная относительно конструктивной
семантики Маркова - Шанина:
А↔∃e(e r A)
+ w-правило
• w-правило: из А(0), А(1), … вывести ∀x А(x).
Курс «Неклассические логики»
Тема «Конструктивные логики»
9

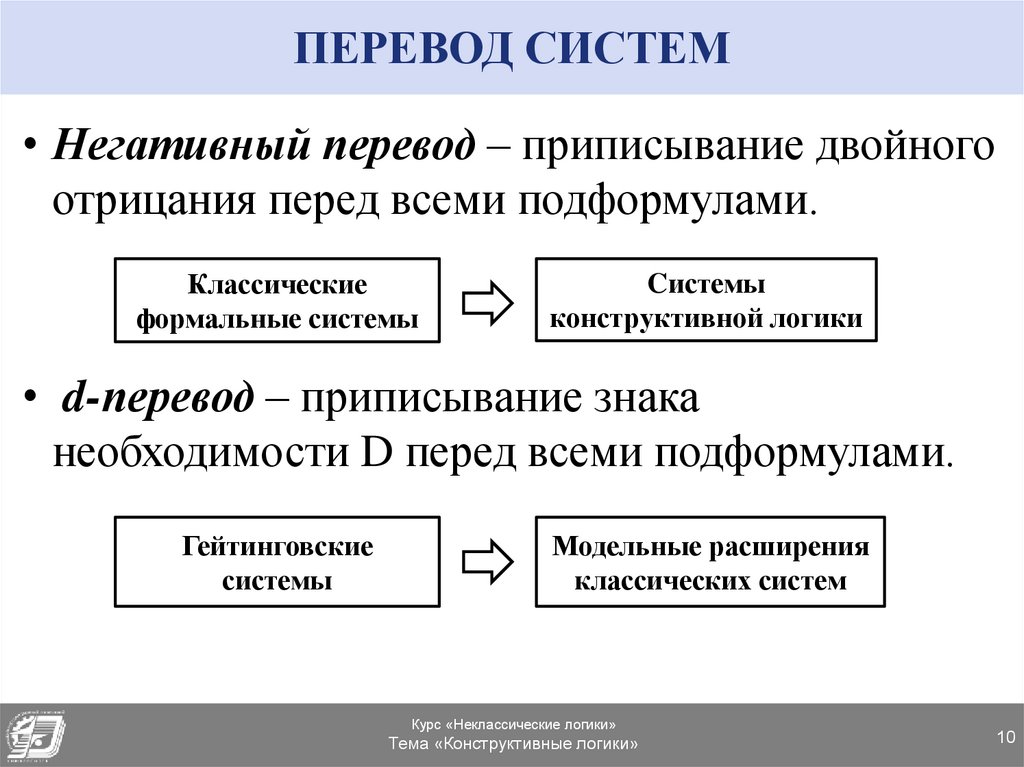
10. ПЕРЕВОД СИСТЕМ

• Негативный перевод – приписывание двойного
отрицания перед всеми подформулами.
Классические
формальные системы
Cистемы
конструктивной логики
• d-перевод – приписывание знака
необходимости D перед всеми подформулами.
Гейтинговские
системы
Модельные расширения
классических систем
Курс «Неклассические логики»
Тема «Конструктивные логики»
10

11. НЕПРОТИВОРЕЧИВОСТЬ СИСТЕМ

• В некоторых системах конструктивной логики
справедливы суждения, ложные при
классическом истолковании. Такие системы S
сводятся к классическим системам So с помощью
подходящего понятия реализуемости.
Понятие реализуемости p:
• Доказывают, что S A влечет существование t
такого, что So (tpA).
Если A-числовое равенство, то So (A↔tpA).
Курс «Неклассические логики»
Тема «Конструктивные логики»
11

12. ОТРИЦАНИЕ

Традиционное ¬
Основано на приведении к противоречию.
• Сильное ~
Предусматривает построение контрпримера.
Для сильного отрицания справедливы многие
из законов классической логики, но теорема об
эквивалентной замене верна лишь в виде:
((p↔q)&(~p↔~q))⊃(A(p)↔A(q))
Курс «Неклассические логики»
Тема «Конструктивные логики»
12

13. ЛОГИКА ГРИССА – НЕЛЬСОНА

• Безотрицательная логика Грисса – Нельсона
стремится избежать использования отрицания и
ограничить класс свойств, о которых делаются
утверждения, такими, для которых уже
построены объекты, удовлетворяющие
свойствам.
→
• Язык такой логики содержит связку x причем
A→B
x понимается как ∀x(A⊃B)&∃xA.
Курс «Неклассические логики»
Тема «Конструктивные логики»
13

14. ТЕОРИЯ КОНСТРУКЦИЙ

Теория конструкций исследует сами правила
построения и доказательства, лежащие в основе
конструктивной математики.
• Конструкции строятся из исходных с помощью
фиксированного набора комбинаторов и
операции применения функции к аргументу.
• Формулы строятся из равенства с помощью
связок логики высказываний и предиката
доказуемости.
Курс «Неклассические логики»
Тема «Конструктивные логики»
14

15. БЕСКВАНТОРНЫЕ СИСТЕМЫ

Цель:
• Получить финитные доказательства суждений.
• Получить мажорант суждений.
Многие традиционные S конструктивной логики погружаются в
бескванторные S~ таким образом, что выводимость в S-суждения
∀x∃yR(x,y) с бескванторной формулой R влечет выводимость в Sформулы R(x,j(x)) для подходящего j.
S – примитивно рекурсивная арифметика
(S – арифметика без индукции).
S – система гёделевских примитивно рекурсивных
функционалов (S – гейтинговская арифметика).
Курс «Неклассические логики»
Тема «Конструктивные логики»
15

16. ТЕОРЕМЫ НОРМАЛИЗАЦИИ

Для формальных систем конструктивной
логики:
• Любой вывод может быть конечным
числом стандартных преобразований
(редукций) приведен к нормальной форме,
не содержащей «лишних» участков.
• Нормальные выводы обладают свойством
подформульности.
Курс «Неклассические логики»
Тема «Конструктивные логики»
16

17. ЗАКЛЮЧЕНИЕ

• Имеются связи между конструктивной
логикой и теорией категорий. Так, понятию
«декартовой замкнутой категории»
соответствует гейтинговское исчисление
высказываний.
• Иногда к конструктивной логике относят все
логические рассмотрения, в которых
требуется, чтобы все изучаемые объекты были
конструктивными, независимо от
применяемой логики.
Курс «Неклассические логики»
Тема «Конструктивные логики»
17

18.

СПАСИБО ЗА ВНИМАНИЕ
© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2014
© Исенбаева Елена Насимьяновна, 2014