Jordan Form

1.

Find the Jordan form and a Jordan basis for the matrix
1 4 0
0 3 0
A 0 4 1
3 9 4
1 5 4
0 0
0 0
0 0
2 1
1 4
1.Find the Eigenvalues of the Matrix
1
4
0
3
det( A I ) 0
4
3
9
1
5
0
0
1
4
4
0
0
0
2
1
0
0
0 5 7 4 10 3 18 2 27 27
1
4
det( A I ) ( 1) 2 ( 3)3 0
2.Determine the Algebraic Multiplicities
1: A lg ebraicMultiplicity 2
3 : A lg ebraicMultiplicity 3
and
3.Find the Eigenvectors and Generalized Eigenvectors
0 0
0
0 0
0
0 0 * X 0
3 1
0
0
1 5
This means that the geometric multiplicity the number of linearly independent eigenvectors
Eigenvectors
1:
0 4 0
0 4 0
0 4 0
3 9 4
1 5 4
1
1
0
0
Х 0 x4 1 x5
1
0
1
0
matches the algebraic multiplicity the multiplicity of the eigenvalue .
In this case, there is no need to look for generalized eigenvectors.

2.

3:
4 4 0 0 0
0
0 0 0 0 0
0
0 4 4 0 0 * Х 0
3 9 4 1 1
0
1 5 4 1 1
0
1
1
1
1
Х 1 x4 1 x 5
2
0
2
0
The algebraic multiplicity is 3, so the geometric multiplicity is less than the algebraic multiplicity.
This indicates that a generalized eigenvector must be found to complete the basis set.
Generalized Eigenvectors (A- I) k
3 : ( A 3I ) 2 X 0
check that (A- I)X 0
4 4 0 0 0 4 4 0 0 0 16 16 0
0
0
0 0 0 0 0 0 0 0 0 0 0
0 4 4 0 0 0 4 4 0 0 0
16 16
3 9 4 1 1 3 9 4 1 1 16 32 16
1 5 4 1 1 1 5 4 1 1 0 16 16
4 4 0 0 0 1 0
0 0 0 0 0 1 0
0 4 4 0 0 1 0 0
3 9 4 1 1 0 2
1 5 4 1 1 0 2
To construct a Jordan chainfor the given generalized eigenvector
0
0
0
0
0
0
0
0
0
0
1
1
X 1
0
0

3.

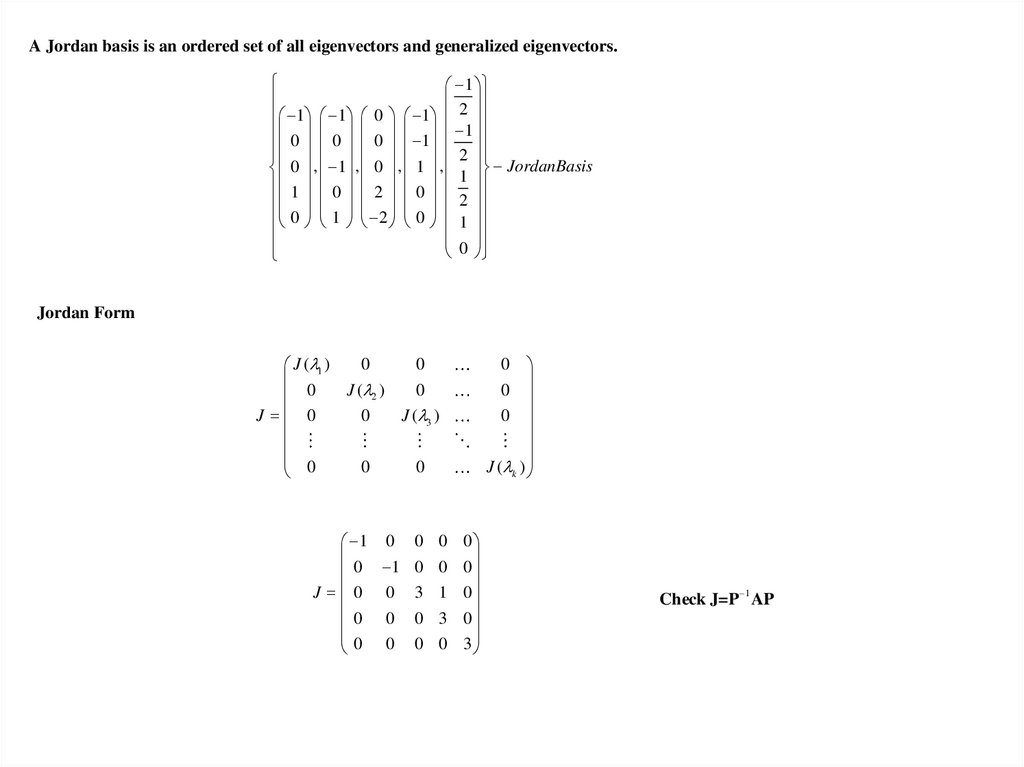
A Jordan basis is an ordered set of all eigenvectors and generalized eigenvectors.
1
1 1 0 1 2
0 0 0 1 1
2
0 , 1 , 0 , 1 , 1 JordanBasis
1 0 2 0
2
0 1 2 0 1
0
Jordan Form
0
0
J ( 1 )
J ( 2 )
0
0
J 0
0
J ( 3 )
0
0
0
1 0
0 1
J 0 0
0 0
0 0
0
0
3
0
0
0
0
1
3
0
J ( k )
0
0
0
0
0
0
0
3
Check J=P 1 AP