Похожие презентации:
Introduction to vectors
1. Introduction to Vectors
Karashbayeva Zh.O.2. What are Vectors?
• Vectors are pairs of a direction and amagnitude. We usually represent a vector
with an arrow:
• The direction of the arrow is the direction
of the vector, the length is the magnitude.
3. Vectors in Rn
Vectors in Rn=1
n
R1-space = set of all real numbers
(R1-space can be represented geometrically by the x-axis)
n=2
( x1 , x2 )
R2-space = set of all ordered pair of real numbers
n=3
(R2-space can be represented geometrically by the xyplane)
R3-space = set of all ordered triple of real numbers ( x1 , x2 , x3 )
n=4
(R3-space can be represented geometrically by the xyzspace)
4
R -space = set of all ordered quadruple of real numbers ( x1 , x2 , x3 , x4 )
4. Multiples of Vectors
Given a real number c, we can multiply avector by c by multiplying its magnitude by
c:
2v
v
-2v
Notice that multiplying a vector by a
negative real number reverses the direction.
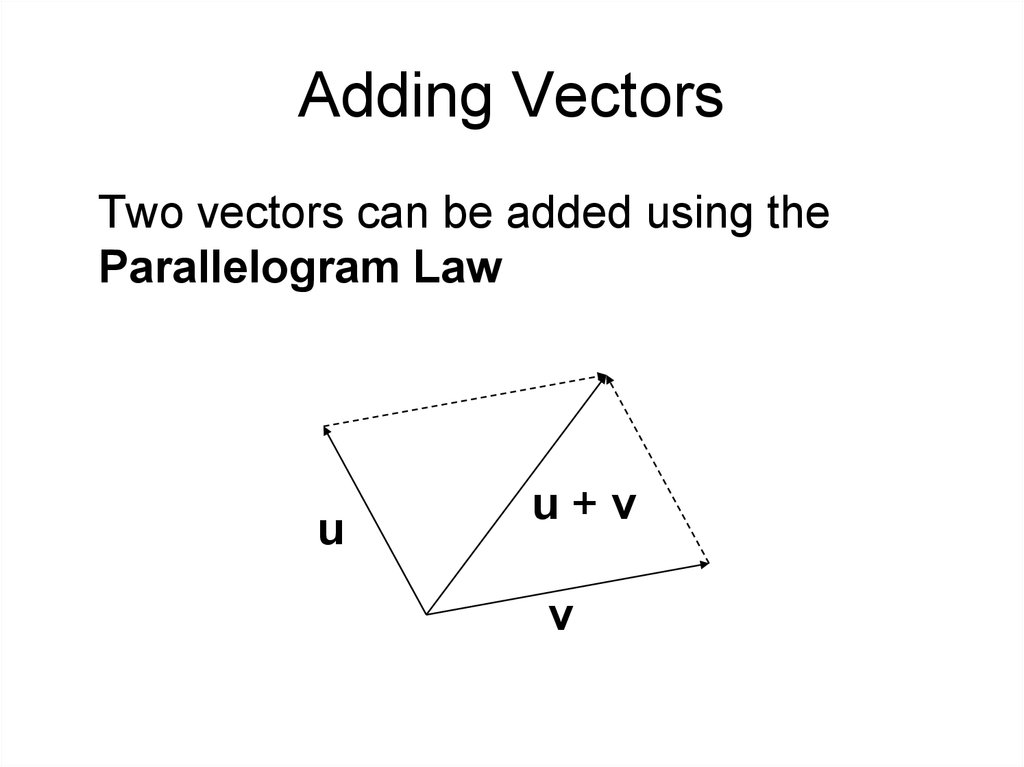
5. Adding Vectors
Two vectors can be added using theParallelogram Law
u
u+v
v
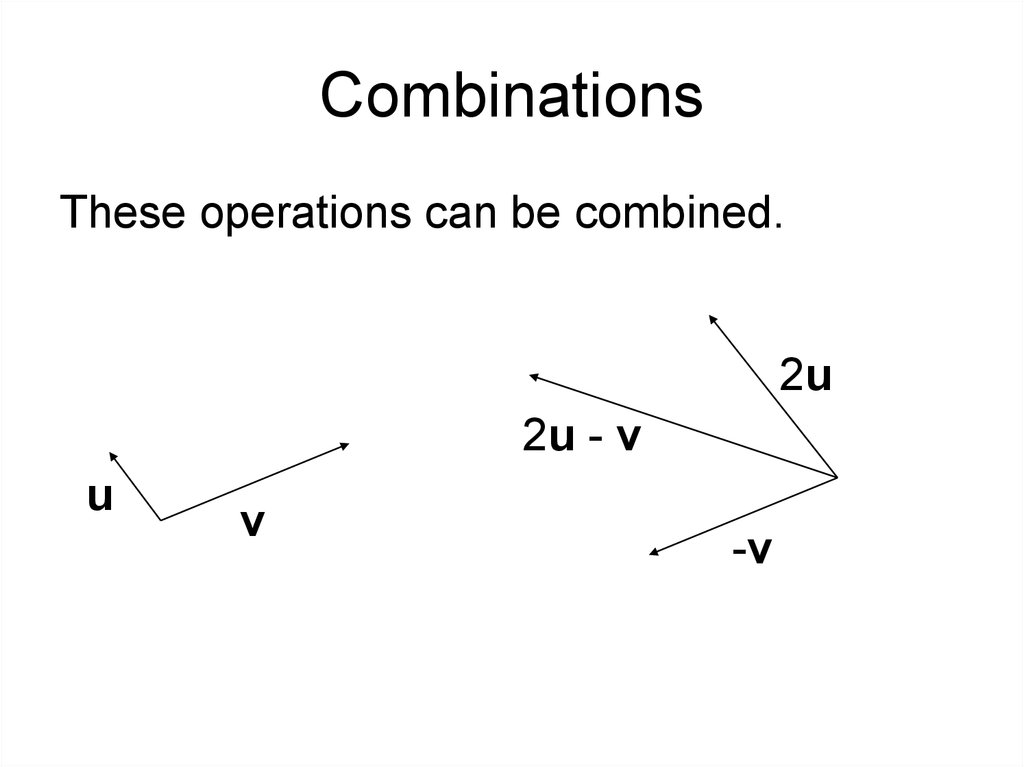
6. Combinations
These operations can be combined.2u
2u - v
u
v
-v
7. Components
To do computations with vectors, we placethem in the plane and find their
components.
v
(2,2)
(5,6)
8. Components
The initial point is the tail, the head is theterminal point. The components are
obtained by subtracting coordinates of the
initial point from those of the terminal
(5,6)
point.
v
(2,2)
9. Components
The first component of v is 5 -2 = 3.The second is 6 -2 = 4.
We write v = <3,4>
v
(2,2)
(5,6)
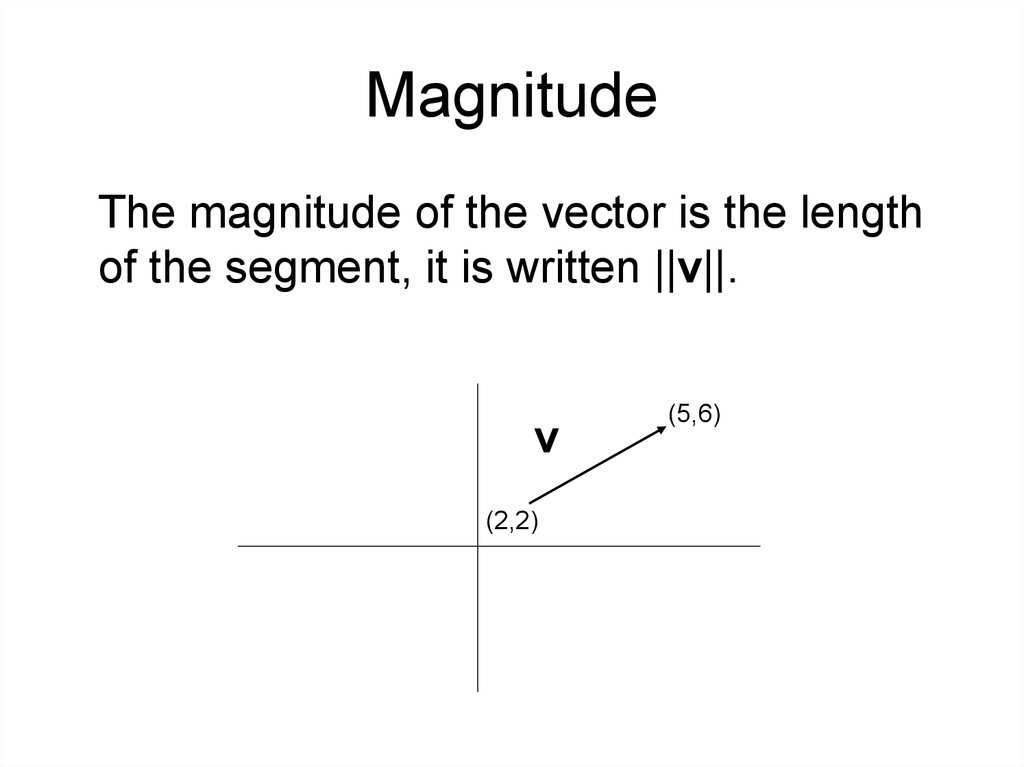
10. Magnitude
The magnitude of the vector is the lengthof the segment, it is written ||v||.
v
(2,2)
(5,6)
11. Scalar Multiplication
Once we have a vector in componentform, the arithmetic operations are easy.
To multiply a vector by a real number,
simply multiply each component by that
number.
Example: If v = <3,4>, -2v = <-6,-8>
12. Addition
To add vectors, simply add theircomponents.
For example, if v = <3,4> and w = <-2,5>,
then v + w = <1,9>.
Other combinations are possible.
For example: 4v – 2w = <16,6>.
13. Unit Vectors
A unit vector is a vector with magnitude 1.Given a vector v, we can form a unit vector
by multiplying the vector by 1/||v||.
For example, find the unit vector in the
direction <3,4>:
14. Special Unit Vectors
A vector such as <3,4> can be written as3<1,0> + 4<0,1>.
For this reason, these vectors are given
special names: i = <1,0> and j = <0,1>.
A vector in component form v = <a,b> can
be written ai + bj.
15.
16.
17. Spanning Sets and Linear Independence
Linear combination :A vector u in a vector space V is called a linear combination of
the vectors v1 , v 2 ,
, v k in V if u can be written in the form
u c1v1 c2 v 2
where c1 , c2 ,
ck v k ,
, ck are real-number scalars
18.
Ex : Finding a linear combinationv1 (1,2,3) v 2 (0,1,2) v 3 ( 1,0,1)
Prove (a) w (1,1,1) is a linear combination of v1 , v 2 , v 3
(b) w (1, 2,2) is not a linear combination of v1 , v 2 , v 3
Sol:
(a) w c1v1 c2 v 2 c3 v3
1,1,1 c1 1,2,3 c2 0,1,2 c3 1,0,1
(c1 c3 , 2c1 c2 , 3c1 2c2 c3 )
c1
c3
2c1 c2
3c1 2c2 c3
1
1
1
19.
1 0 1 1G.-J. E.
2 1 0 1
3 2 1 1
1 0 1 1
0 1 2 1
0 0 0 0
c1 1 t , c2 1 2t , c3 t
(this system has infinitely many solutions)
t 1
w 2 v1 3 v 2 v 3
t 2
w 3v1 5v 2 2 v 3
20.
(b)w c1 v1 c2 v 2 c3 v 3
1 0 1 1
G.-J. E.
2 1 0 2
3 2 1
2
1 0 1 1
0 1 2 4
0 0 0
7
This system has no solution since the third row means
0 c1 0 c2 0 c3 7
w can not be expressed as c1v1 c2 v2 c3 v3
21.
Thespan of a set: span(S)
If S={v1, v2,…, vk} is a set of vectors in a vector space V,
then the span of S is the set of all linear combinations of
the vectors in S,
span(S ) c1v1 c2 v 2
ck v k
ci R
(the set of all linear combinations of vectors in S )
Definition of a spanning set of a vector space:
If every vector in a given vector space V can be written as a
linear combination of vectors in a set S, then S is called a
spanning set of the vector space V
22.
Note: The above statement can be expressed as followsspan( S ) V
S spans (generates) V
V is spanned (generated) by S
S is a spanning set of V
Ex 4:
(a) The set S {(1, 0, 0), (0,1, 0), (0, 0,1)} spans R3 because any vector
u (u1 , u2 , u3 ) in R3 can be written as
u u1 (1, 0, 0) u2 (0,1, 0) u3 (0, 0,1)
(b) The set S {1, x, x 2 } spans P2 because any polynomial function
p( x) a bx cx 2 in P2 can be written as
p( x) a(1) b( x) c( x 2 )
23.
Ex 5: A spanning set for R3Show that the set S (1,2,3),(0,1,2),( 2,0,1) spans R3
Sol:
We must determine whether an arbitrary vector u (u1 , u2 ,u3 )
in R 3 can be expressed as a linear combination of v1 =(1,2,3),
v 2 =(0,1,2), and v 3 ( 2, 0,1)
If u c1v1 c2 v 2 c3 v3 c1
2c3 u1
2c1 c2
u2
3c1 2c2 c3 u3
The above problem thus reduces to determining whether this
system is consistent for all values of u1 , u2 , and u3
24.
1 0 2A 2 1
3 2
0 0
1
Ax u has exactly one solution for every u
span( S ) R3
25.
Definitionsof Linear Independence (L.I.) and Linear Dependence
(L.D.) :
S v1 , v2 ,
For c1v1 c2 v 2
, vk : a set of vectors in a vector space V
ck v k 0
(1) If the equation has only the trivial solution (c1 c2
then S (or v1 , v 2 ,
ck 0)
, v k ) is called linearly independent
(2) If the equation has a nontrivial solution (i.e., not all zeros),
then S (or v1 , v 2 ,
, v k ) is called linearly dependent (The name of
linear dependence is from the fact that in this case, there exist a v i
which can be represented by the linear combination of {v1 , v 2 ,
v i 1 ,
v k } in which the coefficients are not all zero.
, v i 1 ,
26.
Ex : Testing for linear independenceDetermine whether the following set of vectors in R3 is L.I. or L.D.
S v1 , v 2 , v 3 1, 2, 3 , 0, 1, 2 , 2, 0, 1
Sol:
c1
c1v1 c2 v 2 c3 v 3 0
2c3 0
2c1 c2
0
3c1 2c2 c3 0
1 0 2 0
1 0 0 0
0 1 0 0
G.-J. E.
2 1 0 0
3 2 1 0
0 0 1 0
c1 c2 c3 0 only the trivial solution
(or det(A) 1 0, so there is only the trivial solution)
S is (or v1, v 2 , v3 are) linearly independent
27.
• EX: Testing for linear independenceDetermine whether the following set of vectors in P2 is L.I. or L.D.
S v1 , v 2 , v 3 1 x 2 x 2 ,2 5 x x 2 ,x x 2
Sol:
c1v1+c2v2+c3v3 = 0
i.e., c1(1+x – 2x2) + c2(2+5x – x2) + c3(x+x2) = 0+0x+0x2
c1+2c2
=0
c1+5c2+c3 = 0
–2c1– c2+c3 = 0
1 2
1 2 0 0
G. E.
1 5 1 0
0 1
2 1 1 0
0 0
0
1
0
3
0 0
0
This system has infinitely many solutions
(i.e., this system has nontrivial solutions, e.g., c1=2, c2= – 1, c3=3)
S is (or v1, v2, v3 are) linearly dependent
28. Basis and Dimension
• Basis :Basis and Dimension
Spanning
Sets
V: a vector space
S ={v1, v2, …, vn} V
(1)
(2)
Bases
Linearly
Independent
Sets
S spans V (i.e., span(S) = V)
(For any u V ,
V
c v =Ax u has a solution (det(A) 0),
i
i
see Ex 5 on Slide 4.44)
S is linearly independent
(For ci vi = Ax 0, there is only the trivial solution (det(A) 0),
S is called a basis for V
Notes:
A basis S must have enough vectors to span V, but not so
many vectors that one of them could be written as a linear
combination of the other vectors in S
29.
Notes:(1) the standard basis for R3:
{i, j, k} i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1)
n
(2) the standard basis for R :
{e1, e2, …, en} e1=(1,0,…,0), e2=(0,1,…,0),…, en=(0,0,…,1)
Ex: For R4, {(1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,0,1)}
30.
(3) the standard basis matrix space:Ex: 2 2 matrix space:
1 0 0 1 0 0 0 0
,
,
,
0 0 0 0 1 0 0 1
(4) the standard basis for Pn(x):
{1, x, x2, …, xn}
Ex: P3(x)
{1, x, x2, x3}
31.
Ex 2: The nonstandard basis for R2Show that S ={v1 ,v 2 }={(1,1), (1, 1)} is a basis for R 2
c1 c2 =u1
(1) For any u=(u1 ,u 2 ) R , c1v1 +c2 v 2 =u
c1 c2 =u 2
2
Because the coefficient matrix of this system has a nonzero determinant, the
system has a unique solution for each u. Thus you can conclude that S spans R2
c1 c2 =0
(2) For c1v1 +c2 v 2 =0
c1 c2 =0
Because the coefficient matrix of this system has a nonzero determinant, you
know that the system has only the trivial solution. Thus you can conclude that S is
linearly independent
According to the above two arguments, we can conclude that S
is a (nonstandard) basis for R2















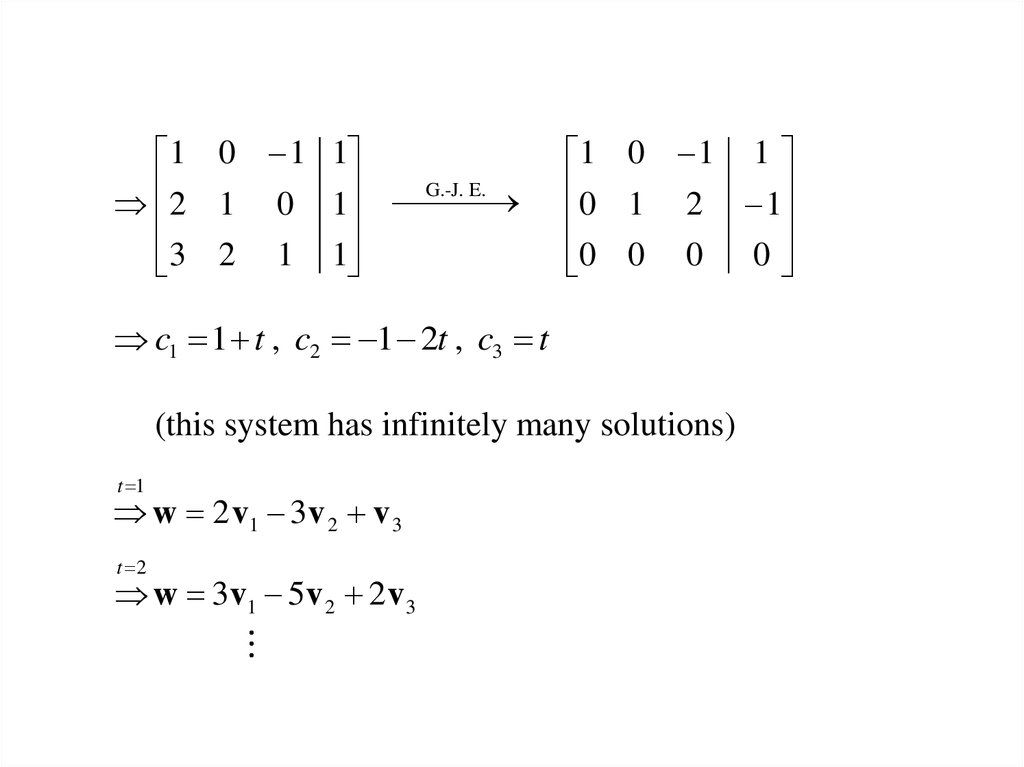












 Математика
Математика








