Обратные задачи вероятностных расчётов конструкций

1.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
КАФЕДРА СТРОИТЕЛЬНОЙ МЕХАНИКИ
ВЕРОЯТНОСТНЫЕ МЕТОДЫ
СТРОИТЕЛЬНОЙ МЕХАНИКИ
И ТЕОРИЯ НАДЁЖНОСТИ
СТРОИТЕЛЬНЫХ
КОНСТРУКЦИЙ
ОБРАТНЫЕ ЗАДАЧИ
ВЕРОЯТНОСТНЫХ РАСЧЁТОВ КОНСТРУКЦИЙ

2.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Основные варианты обратных задач:
Обратная (проектная)
задача вероятностного
расчёта: Определить
вероятностные характеристики входных параметров, обеспечивающие
требуемые характеристики случайных выходных
параметров.
1) определение допустимых вероятностных
характеристик воздействий ( нагрузок );
2) расчёт необходимых статистических показателей
геометрических характеристик сечений (или параметров
глобальной геометрии, структуры, жёсткости и т.п.).
Пример 1
q~
1 1
~
H
a~1
q~a~12
2
~
l
a~2
q~a~2 ~ ~
( l a2 )
2
~,
Определить статистические характеристики нагрузки q
~0,
вызывающей в сечении 1 – 1 фибровое напряжение σ
не превышающее детерминированное значение R с необходимой вероятностью Pσ 0 . Вероятностные свойства
геометрических параметров конструкции известны :
l = 8 M ; Al = 0,001; a1 a2 l /2 4 M ; Aa1 = Aa2 = 0,002;
двутавр № 30 ( A= 46,5 CM2 ; AA = 0,012 ; W= 472 CM3 ; AW = 0,012)
Решение
Фибровое нормальное напряжение в сечении 1 – 1:
~
M(1)
~
M(1) /2
~
M
~
~
|
N
|
|
M
(1)
~ 0 |σ
~(1) N | |σ
~(1) M | ~ ~(1) |
σ
W
A
~
~
l ~ ~ ~
q~ ~ ~ ~
~
|N(1) | q a1 a 2 ; |M(1) | [a 2 ( l a 2 ) a~12 ]
2
2

3.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 1
~ ~
~
~
~ 2
~
~
a
(
l
a
)
a
l
/2
a
a
2
2
1
2
1
~ 0 q~
σ
~
~
σ 0 ({ X }) ;
2W
A
~
~
~
~l a
~1 a
~2 A W } (n 6)
{ X } { q
σˆ 0 uPσ
p (s )
so
Основное расчётное условие:
0
0
~ R ) P ( задано )
P (σ
0
σ
0
~0
σ
Распределение
предполагается
нормальным
σ0 R
σ0 σˆ 0 uPσ R
s0
l l l l ( l l /4) ( l /4)2
Математическое ожидание напряжения: σ 0 q 2 4 4 4
A
2W
ql
q l 1 l 1 D ; D A l
Дисперсия
8
W
A 8W A
(при независимых
0
входных параметрах):
6 σ
σ0 0
xi
i 1
2
xˆ i
X X
σ 0
q
σ 0
a1
l 1 D ;
A 8
X X
q
1 D ;
A 4
X X
σ 0
l
σ 0
a 2
q D
1 4 ;
2
A
X X
q
1 3D ;
4
A
X X
σ 0
A
σ 0
W
ql
2;
A
X X
ql 2
2
8
W
X X

4.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 1
2
q l
σ0
A
2
2
D 2 2 1 D 2 2 1
2 2
1
3
D
D
2
2
2
1 8 Aq 4 1 4 Al 16 1 D Aa1 16 1 4 Aa2 A A 64 AW
B
C
Здесь
Стандарт:
q и Aq – неизвестные, остальное – вычисляемые константы.
σˆ 0 σ 0
ql
A
ql
A
(BA q) 2 C ; основное расчётное условие принимает вид
1 D u
(BAq)2 C R , откуда
Pσ
8
1
R
A
2
q
B uPσ (BAq) C
l
0
0
При заданных значениях входных параметров и R = 200 МПа:
2
2
RA 200 МПа 46,5 см 116,25 кН ; D A l 46,5 см 8 м 78,81; B 1 D 10,851
8м
м
8
W
l
472 см3
2
2
2
2
1
1 3
78,81
4 1
2 78,81
C 10 1
0,1
1
78,81
0,2
1
78,81
0,2
1,2
1,3
4
8
4
2
4
4
= 0,01907
1,071
15,136
9,032
1,44
164,010

5.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 1
Если потребовать выполнения основного расчётного условия
с вероятностью Pσ=0 0,999, то нормированный квантиль u 0,999 = 3,090,
тогда
q
116,25
10,851 3,090 (10,851 Aq)2 0,01907
Координаты границы области
допустимых значений q и Aq
Aq
q , кН/м
0
0,02
0,04
0,06
0,08
0,10
0,15
0,20
10,308
9,982
9,483
9,006
8,569
8,169
7,312
6,616
q
10
8
6
Область допустимых
значений математического
4
ожидания и коэффициента
вариации нагрузки
2
0
0,04
0,08 0,1
0,15
0,2
Aq

6.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 1
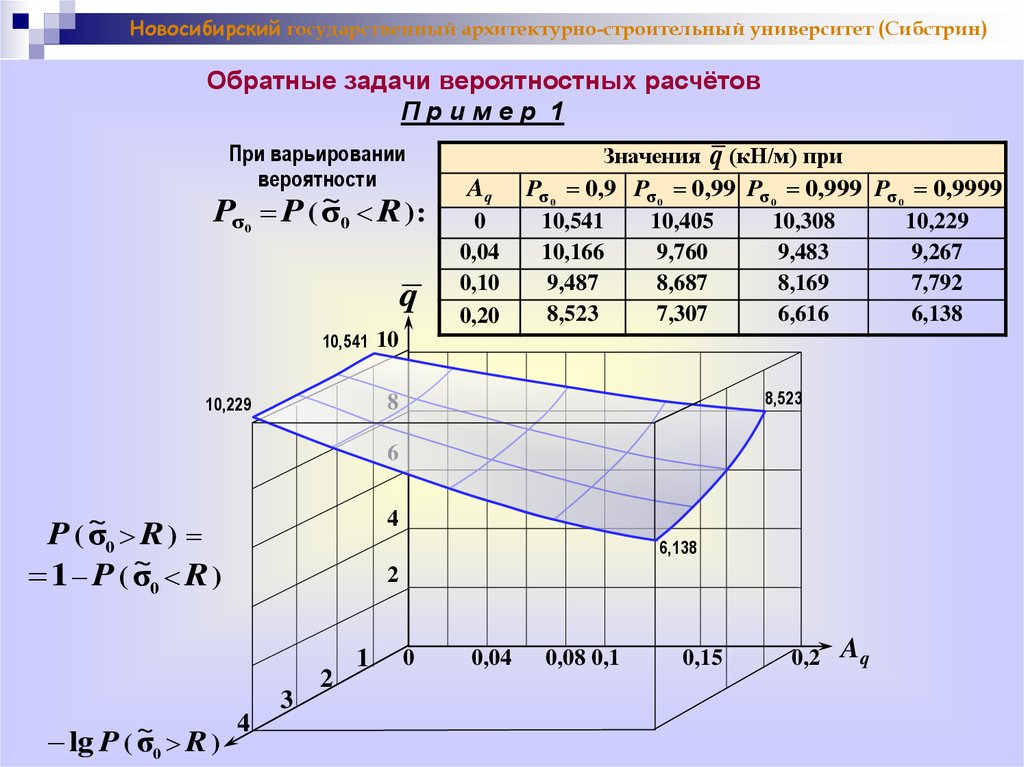
При варьировании
вероятности
~ R ):
Pσ P ( σ
0
0
q
10,541
10,229
Aq
0
0,04
0,10
0,20
Значения q (кН/м) при
Pσ 0 0,9 Pσ 0 0,99 Pσ 0 0,999 Pσ 0 0,9999
10,541
10,405
10,308
10,229
10,166
9,760
9,483
9,267
9,487
8,687
8,169
7,792
8,523
7,307
6,616
6,138
10
8,523
8
6
~ R)
P(σ
0
~ R)
1 P ( σ
0
4
6,138
2
3
~ R) 4
lg P ( σ
0
2
1
0
0,04
0,08 0,1
0,15
0,2
Aq

7.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
q~
Обратные задачи вероятностных расчётов
Пример 2
~
F
~
D
H
~
t
l
~
q~l 2 1 q~a2 F
a
2
8
2
~
M
~
Q
Найти область допустимых значений вероятностных характе~ ~
теристик размеров D и t поперечного сечения стойки рамы,
обеспечивающих коэффициент запаса устойчивости конструкции не менее [ kst ] = 1,2 с необходимой вероятностью Pk st .
У к а з а н и я : слабой изменчивостью габаритных размеров рамы
пренебречь; оценку устойчивости выполнять как для линейно
деформируемой системы.
a
Исходные данные
q 20 кН/м; Aq 0,03; F 15 кН; AF 0,08;
E 2 105 МПа; AE 0,006; l 6 м; a 2 м; H 6 м
~a2 ~
q
Fa
2
Решение
Основное расчётное условие: p
~
~a F
q
~
ΔQ
2
~
3q~l 1 2 a 3 Fa
l 2 l
8
P ( k~st [ k st] ) Pkst ( задано )
~
~ N
k st ~cr
N
kˆ st uPkst
(сжимающие продольные
силы – положительные)
k st kˆ st uPkst [k st]
2
~ ~ 3 8 a a ~ 3a
~
N ΔQ q l 1
2 F 1 ;
8
3l
l
2l
B
k st (kst)
C
[kst] k st
2 ~~
~
π
Ncr EI2
(2H )
kst

8.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 2
Приближённо при
t /D < 1/20 с погрешностью < 1 % :
4
~
~
~
~
4
2t
~
~ πD
π
E
I
kst
~
~ ; I 64 1 1 ~
(2H )2 Bq
l CF
D
2
~
~ 3~
~ πD
t
t
I
1 3 ~
8
D
Математическое ожидание коэффициента устойчивости:
2t 4
kst π 2 E I
; I πD 1 1
64 D
(2H ) Bq l CF
2
4
Дисперсия (при независимых входных параметрах):
4
kst
i 1
kst
q
X X
Стандарт:
kst
xi
B l kst kst
;
F
N
kˆst kst
2
xˆ ;
i
X X
~
~ ~~
{ X } { q~ F E I }
C kst kst
;
E
N
X X
( N B q l CF )
X X
kst kst
;
I
E
X X
2
2
B q l C F
2
2
A
A
q
F AE AI kst
N
N
R
R AI2
kst
I

9.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 2
Основное расчётное условие принимает вид
k st uPkst kst
R AI2 [k st]
k st
[k st]
или
2
1 uPkst R AI
2
[k st] N
I 2H
π E ( 1 uPkst R AI2 )
При заданных входных параметрах и требуемой вероятности Pk st = 0,99 :
N= 117,5 KH ; B = 19/24 ; C = 3/2 ; uPkst= 2,326 , тогда
457,161 см4
I
1 2,326 8,590 10 4 AI2
Координаты
границы области
допустимых
характеристик
момента инерции
сечения
AI
0
0,01
0,02
0,03
0,04
0,05
, CM 4
I
490,61
492.65
498,29
506,58
516,77
528,39
I , CM 4
530
520
510
500
490
480
0
0,01 0,02 0,03 0,04 0,05
AI

10.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 2
Определение области допустимых значений математических ожиданий размеров
2t 4
Так как I πD 1 1 , где D D( AI ), то
64 D
4
D, CM
t , CM
AI = 0
Dmin 2t 4,999
11
1,372
12
0,910
15
0,401
20
0,160
AI = 0,01
5.005
1,381
0,915
0,403
0,161
AI = 0,02 AI = 0,04
5,019
5,065
1,407
1,496
0,928
0,974
0,408
0,425
0,163
0,169
AI = 0.05
5,093
1,555
1,004
0,435
0,174
~
D ~
t
и
64
I
D
t 1 4 1
4
2
πD
t
1,6
1,2
ОДЗ
0,8
AI = 0,05
0,4
0
10
AI = 0
12
15
20
Область допустимых значений параметров , , ADD
и A
tt
Зависимость между коэффициентами AI , AD и At :
2
2
2
2
ˆ 1 I
I
I
1
I
I
ˆ
ˆ
AI
D
tˆ
D
AD t
At
I I D tD t D t tD t D I D tD t D t tD t D
3
3
I
π
D
I
π
D
3
[1 (1 2t /D ) ];
(1 2t /D )3
D D D 16
t D D
8
t t
t t
D

11.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 2
2
2
2t 3 2 2t 2t 3 2
4
AI
1 1 AD 1 At
1 (1 2t /D )4 D
D D
4
(1 Kt3)2 AD2 [(1 Kt )Kt3]2 At2 ; Kt 1 2t
4
D
1 Kt
Если задано отношение
коэффициентов вариации размеров AD / At = n,
то по вычисленному AI находится At :
At = 5AD
10,186
11
12
15
20
5,093
1,555
1,004
0,435
0,174
0,0600
0,0561
0,0506
0,0473
0,0436
5,5
1,6
5,0
1,2
0,8
0,4
4,5
10 11 12
4,36
t, CM
t , CM
4,73
D, CM
6,0
5,06
В рассматриваемой задаче
при AI = 0,05 и n = AD / At = 0,2 :
At , 10 –2
5,61
(1 Kt4)AI
At
4 (1 Kt3)2 ν 2 [(1 Kt )Kt3]2
15
D
20 CM

12.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
q~
~~
EI
l
Обратные задачи вероятностных расчётов
Пример 3
Z1
c~0 ~
Δ l
~
M0
~
M
~ ~
~ от q и Δ
Mq ,Δ
~
~l 2/8
M0(q ,Δ) q
~
~~
в ОСМП M0,1 3EI /l 2
~
M1
от Z1 = 1
В детерминистической
постановке при D = 0:
из условия M0 ≤ ql 2/10
1
3
3
1 c0 l 8 c0 l 2 1
10
8 3C 3C
c0 l 3
48
3C
c0
144 EI
l3
Определить вероятностные характеристики жёсткости
~
c~0 упругой опоры, при которых изгибающий момент M 0
~ и неточнов надопорном сечении балки от
нагрузки
q
~
~~
сти монтажа Δ не превысит q
l 2 /10 с вероятностью PM0.
Исходные данные:
Aq = 0,07; AE = 0,01; AI = 0,015; Δ = 0; Δˆ = 0,0005 l
Решение
~
~
~
По методу перемещений: M0 M0(q ,Δ) M0,1 Z1
~
~
Z1 R 1(q ,Δ) /r~11
~
~
~
6C ~ ~ ~~
10
~
~
~
R 1(q ,Δ) q l c0 Δ ; r11 3 c0 (C EI )
8
l
~
~
10q
~l c~0 Δ
~ 5 q~l c~0 Δ
2
~
~
~ q l 3C 4
Z 1 8 ~
M0
2 ~
8
l
6C ~
6C ~
c0
3 c0
l
l3
Математическое ожидание:
2 ~ 3
~
~~
3
2
q l c0 l
c
l
q
l
0
8 c0 Δl
~
8
8 3C
8 3C
~
M0
M
3
0
~
3
c0 l
c0 l
~ 2
2
3C
3C

13.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 3
Дисперсия изгибающего момента при некоррелированных входных параметрах
(по методу статистической линеаризации):
2
4 M
~
0
M0
xi
i 1
M0
q
M0
С
M0
c0
X X
M
0;
q
M0
Δ
X X
~ ~
xˆ i ; { X } { q~ Δ C c~0 }
X X
c0 l M0
8 c0 l M0
c0 l 3
2
2
; где ψ
;
3
q
l
ψ
8
3C
q l c0 l
8
8 3C
1
c0 l 3
10 c0 l M0 c0 l 3
1 10 ψM0
8
2
;
3C
(ψ
8)(ψ
2)
3C 2
3
C
C
1
3
3
3
c l
10 l M0 c0 l
10 ψM0
8 0 2 1
c0 (ψ 8)(ψ 2)
3C
3C
3 C
3
X X
X X
2
Стандарт:
Mˆ 0 M 0
2
ˆ / l)
8
c
(
Δ
10 ψ
A2 A2
Aq2 0
c0
C
q
ψ
8
(ψ
8)(ψ
2)

14.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 3
Основное расчётное условие:
pMo(M0 )
ˆ u
M
0
PM
ˆ u [ M ] q l 2/ 10
M0 M
0
PM
0
M0 [M0]
~
P ( M0 q l 2/10 ) PM0 задано
0
или
0
M0
ˆ0
M
M0 (1 AM0 uPM0 ) [ M0 ] здесьAM0
M0
ψ
8
5
1 u PM
4 ψ 2
0
2
2
ˆ
24
ψ
С
(
Δ
/
l
)
10
ψ
2
2
Aq2 3
A
A
(ψ 8)(ψ 2) C
c0
q
l
ψ
8
1
Полученная зависимость преобразуется к виду, удобному для вычисления
коэффициента вариации жёсткости опоры:
2
2
(ψ 2) 48 ψ 24ψ С (Δˆ / l )
Ac0
(ψ 8) Aq
3
ql
10ψ 5 uPM0
2
2
2
AC

15.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Обратные задачи вероятностных расчётов
Пример 3
При заданных значениях входных параметров и вероятности PM0 = 0,98
uPM 2,054 ; AC2 A2E A2I 0,000325; дополнител ьно q l 3/C 0,8
0
2
(ψ 2)
2
Ac0
(
0,004355
ψ
0,83168ψ 21,7635) 0,000325
10
ψ
AC0
ψ c0 l 3/ (3EI )
AC0
25
0,20667
28
0,14733
30
0,08804
31
0,03953
31,2
0,01706
0,05
31,24
0,00613
0
0,20
0,15
0,10
25
28
30
31
y

16.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)
Приложение
pz (z)
В расчётах надёжности
z≡b
0
≡
z
z
Вероятность
характеристика безопасности )
z
Pf = 0,5 – F0 ( z )
z
10 – 7
10 – 6
10 – 5
0,0001
0,0005
5,2
4,79
4,265
3,719
3,291
0,001
0,002
0,005
0,01
0,02
0,05
3,090
2,878
2,576
2,326
2,054
1,645
0,1
1,282
5,2
5
4,79
4,265
4
3,719
3,090
3
2,326
2
1,282
1
–7
Pf ≈ 10 –b
–6
–5
–4
–3
–2
–1
–0,301
0
lg Pf
при b = 1 … 4 (из зарубежных
Более точно (ВГС):
источников)
Pf ≈ 10 – ( b /4 + 0,6
2
при b = 1 … 5

17.

Новосибирский государственный архитектурно-строительный университет (Сибстрин)