Похожие презентации:
Динамические задачи. Сопротивление материалов
1. Сопротивление материалов
Федеральное государственное бюджетное образовательное учреждениевысшего профессионального образования
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра сопротивления материалов
ЛЕКЦИЯ № 2С-8
Динамические задачи
Сопротивление материалов
Слайды видеолекций
для студентов технических направлений
Санкт-Петербургский государственный политехнический университет
2014
Санкт-Петербургский государственный политехнический университет, 2014 ©
2. Задачи динамики машин и строительных сооружений
Многократное приложение нагрузки (предельное состояние возникает применьших нагрузках, чем при статическом действии внешних сил).
В конструкциях возникают колебания и вибрации (предельные
нагрузки снижаются еще более).
Высокие скорости деформирования (некоторые пластичные
материалы разрушаются хрупко, без заметных остаточных
деформаций).
2
3. Расчет элементов конструкций при постоянных ускорениях
3ma N P
N
2
А
1
А
N – нормальная сила в
поперечном сечении каната;
Р и m – вес и масса кабины
лифта и каната.
В соответствии с принципом
Даламбера введем силу инерции
l
FИ ma
C
P
x
Fи
N P FИ 0
y
3
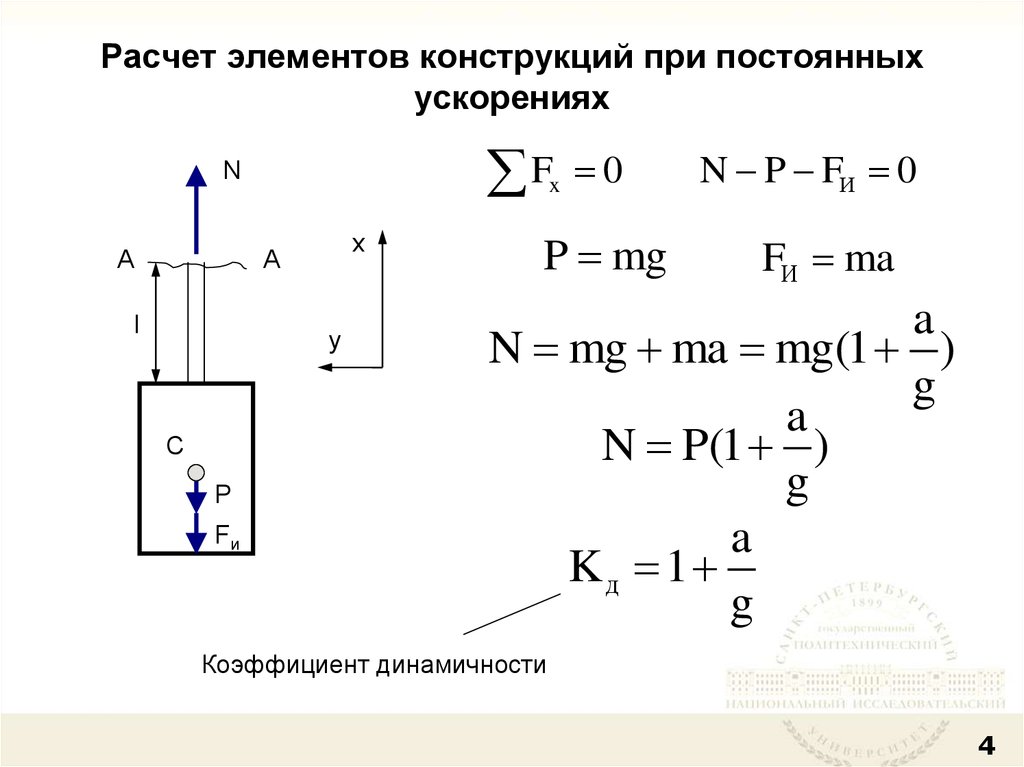
4. Расчет элементов конструкций при постоянных ускорениях
FN
А
x
x
А
l
y
C
P
Fи
0
P mg
N P FИ 0
FИ ma
a
N mg ma mg(1 )
g
a
N P(1 )
g
a
Kд 1
g
Коэффициент динамичности
4
5.
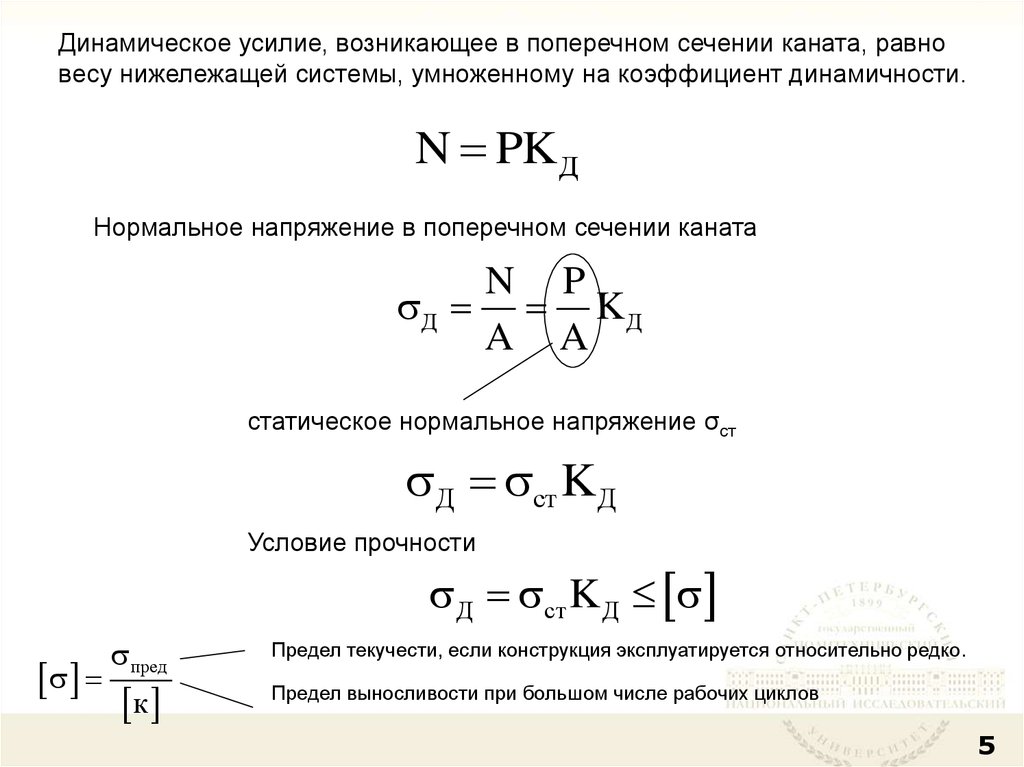
Динамическое усилие, возникающее в поперечном сечении каната, равновесу нижележащей системы, умноженному на коэффициент динамичности.
N PKД
Нормальное напряжение в поперечном сечении каната
N P
Д K Д
A A
статическое нормальное напряжение σст
Д ст KД
Условие прочности
Д ст K Д
пред
к
Предел текучести, если конструкция эксплуатируется относительно редко.
Предел выносливости при большом числе рабочих циклов
5
6. Ударное взаимодействие упругих тел
Если время внешнего воздействия на конструкцию невелико (поотношению к периоду собственных колебаний), то совокупность
механических явлений называется ударом.
Упругий буфер должен
остановить груз, движущийся
горизонтально со скоростью
v.
xmax
x
v
x
m
cr
F c x
с
y
где с – жёсткость линейно упругого буфера.
6
7.
Движущийся груз обладает кинетической энергиейxmax
x
x
T
v
m
1 2
mv
2
Потенциальная энергия упругой
деформации буфера в момент его
наибольшего обжатия
y
U max
1
Fmax xmax
2
К моменту полной остановки груза имеем Т = 0 и U = Umax. По
закону сохранения энергии можно записать
U max T
Fmax v mc
1
1 2
Fmax xmax mv
2
2
xmax
m
v
c
7
8.
• Чем больше жёсткость буфера, тем большевозникающее в нём усилие с одновременным
уменьшением осадки.
• И, наоборот: с уменьшением жёсткости (с
увеличением податливости λ = 1/с) возрастает осадка
буфера и уменьшается действующее усилие.
8
9. СКРУЧИВАЮЩИЙ УДАР
ωМРассмотрим прямой стержень, один
конец которого заделан, а на другом
конце вращается маховик с угловой
скоростью ω
Пусть имеется устройство, которое
позволяет сцепить вращающийся
маховик со свободным концом стержня.
Стержень закручивается.
силе F сопоставим обобщённую силу М (вращающий момент),
перемещению х – обобщённое перемещение φ (угол закручивания),
жёсткости с – обобщённую жёсткость
c
M
массе m – момент инерции маховика относительно оси вращения х
J x 2 dm
m
где m – масса маховика, ρ – расстояние элементарной массы dm от оси
вращения х.
9
10. СКРУЧИВАЮЩИЙ УДАР
ωМc
M
J x 2 dm
m
xmax
max
Jx
m 2
v
m
v
c
Fmax v mc
Jx
c
M max J x c
10
11. УДАР ВЕРТИКАЛЬНО ПАДАЮЩИМ ГРУЗОМ
mH
xmax
• Рассмотрим задачу о грузе, падающем
под действием силы тяжести на упругий
буфер
U UП
Потенциальная энергия положения
1
Fmax xmax P( H xmax )
2
Р – вес груза, H – расчётная высота падения.
1 2
cxmax Pxmax PH 0
2
P P 2 2cPH
xmax
c
Знак «плюс» соответствует нижнему положению груза при колебаниях, где
сила веса и сила инерции совпадают по направлению
11
12.
xmaxP P 2 2cPH
c
Вынесем за скобки множитель Р/с
xmax
P
2cH
1 1
c
P
Отношение Р/с - статическая деформация
x СТ
P
c
Величина хСТ соответствует случаю, когда на буфер аккуратно укладывается
рассматриваемый груз весом Р.
x max
2H
x СТ 1 1
x СТ
12
13.
x max2H
x СТ 1 1
x СТ
Коэффициент динамичности
2H
K 1 1
x СТ
Максимальная осадка упругого элемента при ударе падающим грузом
x max x СТ K
Fmax FСТ K
FСТ P
При Н = 0, получаем Кд = 2.
Следовательно, если груз медленно довести до соприкосновения с упругой
системой, а затем внезапно сбросить, то усилие в системе удваивается по
сравнению со спокойным укладыванием этого груза.
13
14. НАПРЯЖЕНИЯ ПРИ УДАРЕ
Нормальное напряжение в момент ударапред
Fmax
[ ]
A
[k ]
[kд] – динамический нормативный коэффициент запаса, который несколько
больше нормативного коэффициента запаса, принятого для конструкций,
работающих при статическом действии нагрузок.
В качестве предельного напряжения σпред принимают либо предел
выносливости σR (при многократных ударах), либо предел текучести σт.
14
15.
Испытания материалов на устойчивость ударным нагрузкамИспытание на изгиб ударной пробы
материала
U-образный надрез
V-образный надрез
U U П U Ph 0 Ph P(h h 0 )
15
16.
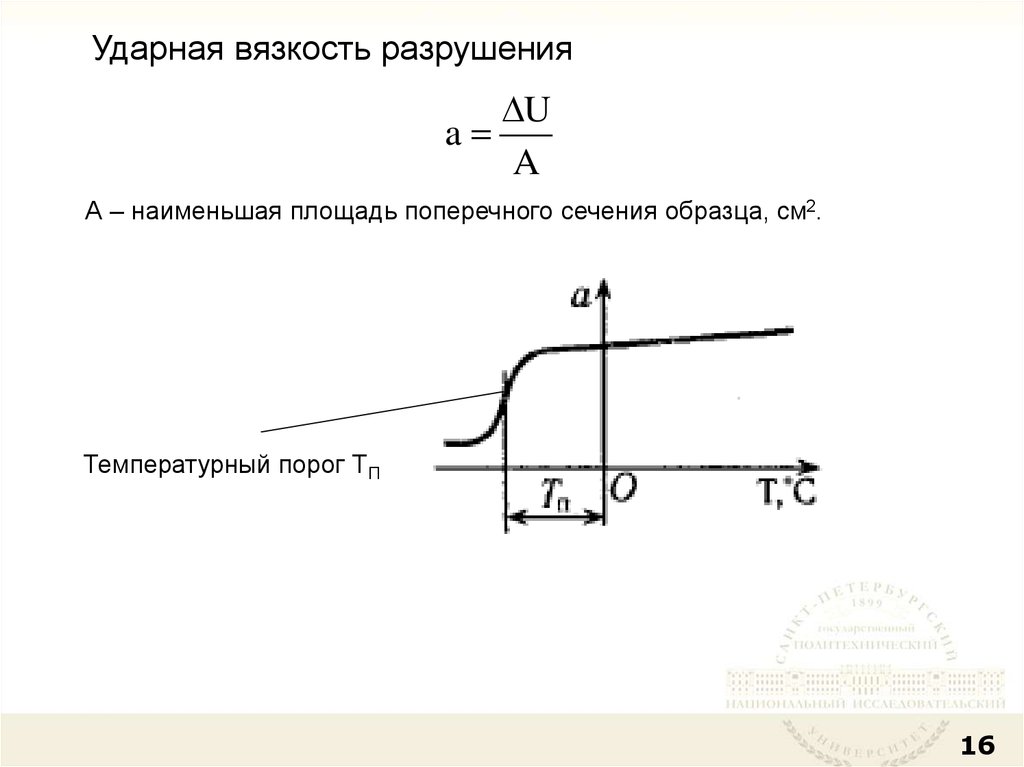
Ударная вязкость разрушенияU
a
A
А – наименьшая площадь поперечного сечения образца, см2.
Температурный порог ТП
16
17.
Влияние скорости деформированияПри ударе характеристики прочности возрастают на 20……..30%,
характеристики пластичности снижаются.
17
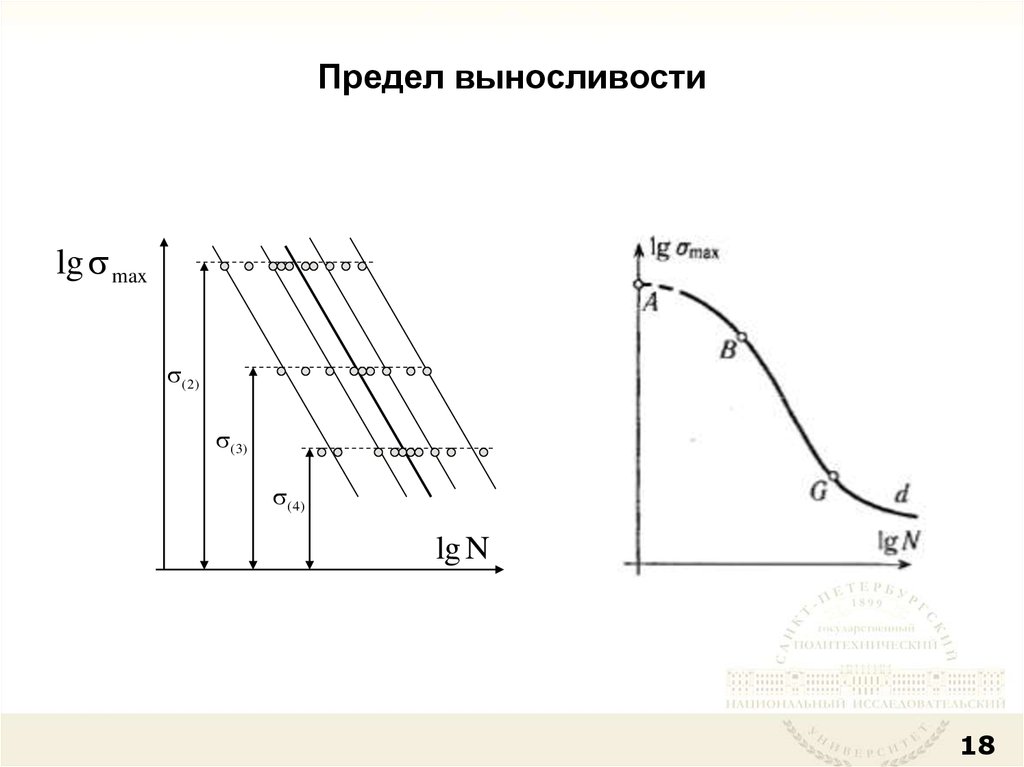
18. Предел выносливости
lg max(2)
(3)
(4)
lg N
18














 Физика
Физика Строительство
Строительство








