Лекция_21

1.

“Исследовательский Центр
имени М.В. Келдыша”
Теория теплообмена
Курс лекций В. Я. Лихушина
Лекция №20
Москва - 2007
1

2.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Возникновение турбулентного режима течения и его особенности
При достаточно больших значениях характерного числа Рейнольдса движение в
пограничном слое носит турбулентный характер.
Переход от ламинарного режима течения к турбулентному происходит вследствие того,
что при больших числах Рейнольдса ламинарное течение перестает быть устойчивым.
Не всякое решение уравнений Навье-Стокса может реально существовать. Реальные
движения должны не только удовлетворять уравнениям движения и соответствующим
граничным условиям, но и должны быть устойчивыми.
При достаточно малых числах Рейнольдса ламинарное стационарное движение вязкой
жидкости или газа всегда устойчиво. Это означает, что всякое возмущение, которое может
возникнуть в движущейся жидкости или газе, с течением времени затухает.
v
Например, если стационарное движение газа имело распределение
скоростей
0 x, y, z ,
а возникшее возмущение привело
к наложению на скорость v0 скорости v x, y, z, , то с
течением времени скорость v в случае устойчивого движения должна уменьшаться и
стремиться к нулю.
Как показывают теория и эксперимент, при числах Рейнольдса, превышающих
некоторое критическое значение Reкp, движение становится неустойчивым.
Движение, которое было стационарным при Re< Reкp, в случае Re> Reкp становится
нестационарным: на стационарное движение накладывается нестационарное
возмущающее движение с возрастающей по времени амплитудой.
2

3.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Возникновение турбулентного режима течения и его особенности
Если число Рейнольдса хотя и больше Reкp, но близко к нему, то возмущающее
движение является периодическим с определенной характерной частотой 1.
Поскольку жидкость движется со скоростью v0 , то возмущающее движение
характеризуется также масштабом l1 , периодичности в пространстве.
Масштаб l1 характеризует расстояние, на протяжении которого в данный момент
скорость возмущающего движения изменяется от некоторого максимума до минимума и
снова до максимума.
Исходя из размерности l1 по порядку величины должно быть равно характерному
U
линейному размеру задачи, то есть l1 ~ l , а 1 ~ , где U характерная скорости потока.
l1
Физически ясно, что возрастание амплитуды возмущающего движения не может
происходить неограниченно. Как только амплитуда возмущающего движения
становится достаточно большой, само возмущающее движение становится
неустойчивым и на него накладывается новое возмущающее движение с частотой 2 >
1 и с характерным линейным масштабом l2 l1. Возмущающее движение с частотой 2
возникает при числе Re несколько большем, чем то, которое соответствует
возникновению движения с частотой 1 .
3

4.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Возникновение турбулентного режима течения и его особенности
При дальнейшем увеличении числа Re нарушается устойчивость и второго
пульсационного движения. В результате возникает третье пульсационное движение с
частотой 3 > 2 > 1 и масштабом l3 <l2 <l1.
Заметим, что 1, 2, 3, вообще говоря, не кратны и не соизмеримы (т.е. их отношения
не равны рациональным числам). С возрастанием числа Рейнольдса появляются
последовательно все новые и новые периодические возмущения, в результате чего
движение жидкости приобретает весьма сложный и запутанный характер. Происходит
постепенный переход от ламинарного режима течениия к турбулентному.
Турбулентность - это трехмерное нестационарное движение, в котором вследствие
растяжения вихрей создается непрерывное распределение пульсаций скорости в
интервале длин волн от минимальных, определяемых вязкими силами, до максимальных,
определяемых граничными условиями течения. Она является обычным состоянием
движущейся жидкости, за исключением течений при малых числах Рейнольдса.
Характерной особенностью турбулентного движения является :
каскадный процесс передачи энергии от вихрей большего масштаба к вихрям
меньшего вплоть до самых мелких вихрей, в которых происходит диссипация
механической энергии в тепло.
4

5.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Возникновение турбулентного режима течения и его особенности
Из описанной качественной картины возникновения турбулентного режима
течения следует, что при развитой турбулентности имеют место следующие
характерные процессы:
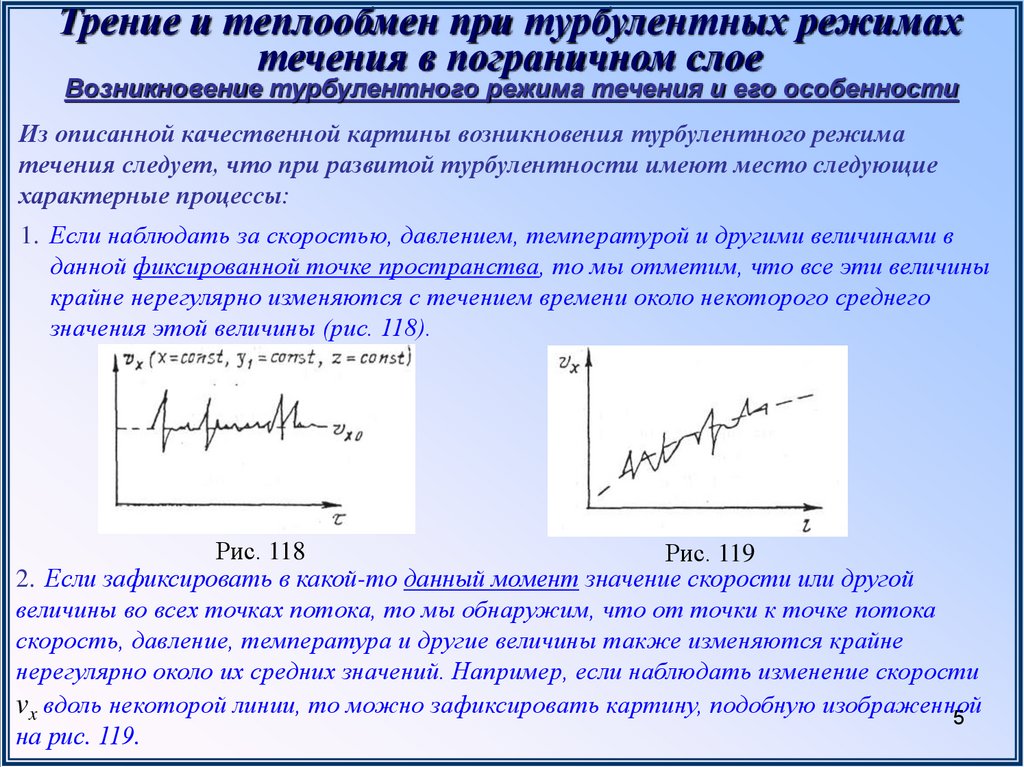
1. Если наблюдать за скоростью, давлением, температурой и другими величинами в
данной фиксированной точке пространства, то мы отметим, что все эти величины
крайне нерегулярно изменяются с течением времени около некоторого среднего
значения этой величины (рис. 118).
Рис. 118
Рис. 119
2. Если зафиксировать в какой-то данный момент значение скорости или другой
величины во всех точках потока, то мы обнаружим, что от точки к точке потока
скорость, давление, температура и другие величины также изменяются крайне
нерегулярно около их средних значений. Например, если наблюдать изменение скорости
vx вдоль некоторой линии, то можно зафиксировать картину, подобную изображенной
5
на рис. 119.

6.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Возникновение турбулентного режима течения и его особенности
3. Если же рассматривать поведение отдельной жидкой частицы (моля), как это
делается в методе Лагранжа, то мы убедимся, что траектория частицы при
турбулентном движении чрезвычайно сложна и напоминает траекторию движения
отдельной молекулы газа (рис. 120).
Подобно тому, как описание состояние газа возможно только
статистическими методами, так и теория турбулентного движения
должна опираться на статистические методы.
Рис. 120
Конечной задачей теории турбулентного движения является получение замкнутой
системы уравнений, которая позволяла бы однозначно определить все величины,
характеризующие осредненное движение, т.е. осредненные значения скорости,
энтальпии, температуры, плотности, напряжения трения, удельного теплового
потока и других величин.
Так же, как в случае, когда нам практически не нужно знать движение каждой
отдельной молекулы (да это и невозможно!), а достаточно знать средние величины,
характеризующие движение газа, так и при изучении турбулентных потоков нам не
нужно и невозможно знать, как меняется скорость и другие параметры потока в каждой
его точке с течением времени, а достаточно знать осредненные значения
6
соответствующих величин.

7.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Возникновение турбулентного режима течения и его особенности
Общая задача определения осредненных параметров турбулентного движения
чрезвычайно сложна и до настоящего времени теоретически не решена.
При исследовании турбулентного пограничного слоя на поверхности обтекаемого
тела и пограничного слоя внутри труб и каналов приходится наряду со статистическими
методами пользоваться и рядом экспериментальных зависимостей, т.е. использовать так
называемые полуэмпирические методы расчета трения и конвективного теплообмена в
турбулентном пограничном слое.
Несмотря на приближенный характер, результаты полуэмпирических методов расчета
трения и теплообмена в турбулентном пограничном слое для широких классов течений
довольно хорошо согласуются с экспериментальными данными.
Осреднение
При практическом измерении тех или иных величин мы фактически определяем средние
по времени значения данной величины в данной точке или точнее в ее окрестности.
Поэтому в дальнейшем под средним значением мы будем подразумевать среднее по
времени, например, для составляющей скорости vx :
vx cp vx x, y, z,
t
v x, y, z, d
2
1
x
t
Здесь осреднение проводится по конечному промежутку времени 2 .
7

8.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Возникновение турбулентного режима течения и его особенности
С теоретической точки зрения более строго следовало бы определять среднее значение
каждой функции как ее математическое ожидание. Для определения математического
ожидания нужно знать вероятность реализации каждой случайной функции. Например,
положим для простоты, что каждая данная реализация функции vx x, y, z,
характеризуется конкретным значением параметра 0 1 таким, что d есть
вероятность реализации случайной функции при значениях параметра от до + d .
1
Тогда математическое ожидание
vx x, y, z, vx x, y, z, , d
0
Мы будем полагать, что среднее по времени
и математическое ожидание случайной
функции практически совпадают, хотя строгое совпадение возможно лишь в частных
случаях.
Осреднение по времени, по конечному промежутку времени 2 является весьма
трудной операцией, ибо возникает вопрос, как определять этот промежуток.
Для разных мы, вообще говоря, будем получать разные средние значения. Эта
трудность не возникает, если ограничиться рассмотрением стационарных осредненных
движений, не зависящих от времени. Для таких течений можно выбрать
и
t
полагать, что:
1
vx x, y, z lim
vx x, y, z, d или
2 t
1
vx x, y, z lim
vx x, y, z, d .
0
8

9.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости (Навье-Стокса)
В развитии приближенных методов расчета турбулентного пограничного слоя
большую роль сыграл вывод осредненных уравнений турбулентного движения,
осуществленный впервые Рейнольдсом для несжимаемых потоков. Мы рассмотрим
общий случай сжимаемых потоков.
Ограничиваясь рассмотрением стационарных турбулентных движений газа.
Легко видеть, что для стационарного осредненного движения среднее значение по
времени от производной какой-либо функции по времени равно 0. Например,
1 T
T 0
d
.
T
T
0
При T
t
получаем 0.
Осреднение уравнения неразрывности
Запишем уравнение неразрывности в симметричных обозначениях координат:
vk
0.
xk
Для сокращения записи подразумеваем, что по повторяющемуся индексу
производится суммирование для значений индекса 1,2,3.
Произведем замену:
где
vk vk v k
и vk
T
1
- средние по времени;
d ,
T0
T
1
vk vk d , T
T 0
9

10.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Осреднение уравнения неразрывности
Заметим, что по определению 0 ; vk 0 . Кроме того, , vk vk .
Подставляя значения и vk в уравнение неразрывности, получим:
vk vk 0.
xk
d
vk
vk 0.
Умножая уравнение на
и интегрируя его от 0 до Т,
xk
xk
T
Для плоских течений, полагая x1 = х, х2 = у , получаем: v x v y v x v y 0.
x
y
x
y
Осреднение уравнений движения
v
v
p ik
i vk i
i 1, 2, 3
vi vk
xk
xi xk
v
2 v
ik ki
ik e ik e
xe
xk xi 3 xe
где - первая (сдвиговая) вязкость; - вторая (объемная) вязкость.
В дальнейшем мы для краткости будем называть среднее по времени от произведения
пульсаций двух величин v v корреляцией этих величин.
x y
Совершенно ясно, что при осреднении уравнений движения должны появиться
v
корреляции пульсаций вязкости и пульсаций других величин, например
10
i
xk

11.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Опираясь на данные опыта, мы будем пренебрегать всеми корреляциями, куда входят
пульсации вязкости , , теплопроводности , коэффициента диффузии D или
пульсации скорости диффузии Vx , V y , Vz .
Введем, как и раньше, обозначения vk vk vk ; ; ik ik ik ; где
vi vk 2 ve
v
ik e
ik
ik
xe
xk xi 3 xe
Поскольку пульсациями , , , D
и их корреляциями с другими пульсациями
мы пренебрегаем, то в дальнейшем вместо , , , D будем писать просто , , , D.
Умножим уравнение неразрывности на vi и сложим его с уравнением движения для
v
0.
проекции на i-ю ось, тогда получим: v v v
p
x
k
i
i k
ik
k
xk
xi xk
После подстановки значений ,vi,vk,p, ki и осреднения уравнения по времени :
vi vk
p
vi vk vk vi
ik vi v k ,
xk
xk
xi xk
vk
vk 0.
T vi vk , или, используя уравнение неразрывности, получим:
xk
xk
vi
p
vk vk
ik vi vk vi vk , i 1,2,3.
11
xk
xi xk

12.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Для плоских течений можно записать два уравнения
vx
vx
p
vx v x
v y v y
xx v x v x v x vx
xy v x v y v x v y
x
y
x x
y
v y
v y
p
vx vx
v y v y
yx v y v x v y vx
yy v y v y v y v y .
x
y
y x
y
Нас интересуют не просто осредненные уравнения стационарного турбулентного
движения, а уравнение турбулентного пограничного слоя. Считая, что l оценим
порядок величины членов осредненных уравнений:
1. Будем считать, что при больших сверхзвуковых скоростях ~ ; v y ~ v y ;
U
v y ~ v y ~
l
U v ~ U
2. Предположим также, что v x ~ v y ~
;
x
l
3. Будем считать, что производная по у от турбулентного трения v x v y имеет тот же
порядок, что и инерционные члены в левой части первого уравнения движения (проекция
2
2
U 2 т.е.
на ось х)
и
U
U
2
v x v y ~
v x v y ~
v y ~
y
l
l
l
4.
U U U 2 2
v x v y ~
, т.е. v x v y v x v y .
2
l l
l
12

13.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
U 2 2
v y v y v y2 , поскольку
y2 ~ v x v y
v
v y v y ~
,
т.е.
l2
С учетом проведенных оценок порядков величин отдельных членов уравнение
неразрывности и уравнение движения для турбулентного пограничного слоя можно
v
vx
p v
записать в виде:
vx x v y v y
x v x v x ;
x
y
x y y
p
v y2 0, т.е. p v y2 const p ;
y y
vx
v y v y 0.
x
y
v x
Заметим теперь, что y xy , а член v x v y представляет добавку к ламинарному
трению xy . По смыслу величина v x v y определяет напряжение трения, которое
обусловлено пульсациями скорости. Мы будем называть эту величину для краткости
турбулентным напряжением трения. По аналогии с ламинарным трением мы можем
искусственно ввести понятие о турбулентной вязкости, определив ее из соотношения
v x v y
vx
T
v x v y T
, т.е. по определению
v x
y
13
y

14.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Осредненные уравнения движения и неразрывности для турбулентного пограничного
слоя можно записать в виде:
v
vx
v
p
vx x v y v y
T x ;
x
y
x y
y
p
2
~ 0, если v y мало в сравнении с p , что и будет предполагаться в дальнейшем
y
vx
v y v y 0.
x
y
Коэффициент турбулентной вязкости по своей природе в корне отличается от обычной
вязкости . Обычная вязкость характеризует газ или жидкость как таковые, независимо
от того, какое конкретное движение они совершают.
Турбулентная вязкость T зависит не только от физических свойств жидкости, а прежде
всего от характера движения, совершаемого жидкостью, от характера пульсаций
скорости, от которых зависит v x v y , и от распределения осредненной скорости vx по
vx
координате у, так как от него зависит производная
. Определить теоретически T
y
пока невозможно, поэтому приходится использовать некоторые
закономерности,
полученные экспериментальным путем.
Осреднение уравнения состояния для бинарной смеси
1
p
1
1
R
c1 M T
M
M
2
2
1
Введем, как и раньше ;
c1 c1 c1 ; c2 c2 c2 ; T T T ;
14

15.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Осреднение уравнения состояния для бинарной смеси
После осреднения нетрудно получить следующее соотношение для средних значений
p, , T , c1 :
1
1
1
1
1
1
c1
p R
T
R
c
c1 T
1
M2
M2
M 1 M 2
M 1 M 2
1
1
1
1
1
1
1
1
1
R
c1
c1
c1
c1 T R
T R
c1 T
M2
M2
M2
M 1 M 2
M 1 M 2
M 1 M 2
Опираясь на данные экспериментальных исследований, мы будем пренебрегать в
T , c1 T , c1 , c1 T .
дальнейшем корреляциями:
За счет такого пренебрежения мы будем иметь погрешность, но зато уравнение
состояния можно будет использовать в том же виде, что и обычно:
1
p
1
1
R
c1 M T
M
M
2
2
1
15

16.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнения диффузии для бинарной смеси
c
c
c
c1V1 k D 1
1 vk 1
c1V1 k M 1
xk
xk
xk
k
где V1 - k-я составляющая диффузионной скорости первого компонента.
vk
Используя уравнение неразрывности
xk
0.
уравнение диффузии можно преобразовать, и оно будет иметь вид:
c1 vk c1
c1V1 k M 1
xk
xk
Введем vk vk vk ; ; c1 c1 c1 .
c
k D , c , 1 ,
Как условились раньше будем пренебрегать V1 ,
1
x
k
Тогда легко получить после осреднения по времени
c
c1 vk vk
c1V1 k
vk c1 M 1 где
c1V1 k D 1
xk
xk
xk
xk
Используя осредненное уравнение неразрывности, можем переписать последнее
c1
c
уравнение в виде:
D 1 vk c1 M1
vk vk
xk xk
xk
v k c 1 - дополнительный диффузионный поток первого компонента из-за пульсаций
скорости. Это турбулентный диффузионный поток первого компонента. Можно ввести
v c
в рассмотрение коэффициент турбулентной диффузии:
DT k k 1
c
c
16
1
vk c1 DT k 1
xk
xk

17.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Осреднение уравнения диффузии для бинарной смеси
Заметим, что для каждой из трех осей координат (k= 1, 2, 3) коэффициент турбулентной
диффузии различен. Так же, как и турбулентная вязкость, коэффициент турбулентной
диффузии зависит не только от свойств газа, а прежде всего от характера турбулентных
пульсаций и от распределения осредненной концентрации c1. Вводя формально
коэффициент турбулентной диффузии, получим:
v v xc x D D xc M
k
T
1
k
k
1
1
k
Для двухмерного потока в случае турбулентного пограничного слоя аналогично
предыдущему получим:
c
c
c
vx 1 v y v y 1 D DT k 1 M 1
x
y y
y
Коэффициент турбулентной диффузии пока не может быть вычислен теоретически и
находится из соотношений, полученных экспериментальным путем.
Осреднение уравнения энергии
D ci
h
k
vi
h T
p
k
V
vi
i
vk
ik
ci hiVi ;
ci xk
xk xk xk
xi
xk xk i
D ci
Vi k
Умножая уравнения неразрывности на vi и суммируя с
ci xk
17
уравнением движения, имеем
k
k

18.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Осреднение уравнения энергии
vi vi vk
p ik
xk
xi xk
vi
vk
vk
0
v
h
;
h
h
0,
используя уравнение неразрывности
i
xk
xk
и складывая с уравнением энергии получим:
v
T
p
vi
h
vk h
ik i
ci hiVi k ;
xk
xk xk
xi
xk xk i
vi2
vi2 T
k
h
v
h
v
c
h
V
.
k
i
ik
i
i
i
x x x
2 xk
2
x
k
k
k
k i
2
2
2
2
v
v
v
v
Обозначим H h i ; H h h i i vi vi H h i vi vi
22
2
2
2
vi
vi 2
H h ; H h
vi vi ;
2
2
vi 2
Членом
в выражении для Н мы в дальнейшем пренебрежем, тогда H H h vi vi
2
Произведем замену температуры на энтальпию:
c
T
h
hi i ;
xk c p xk c p
xk
18

19.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Осреднение уравнения энергии
v
vi2 h
ci
k
vi ik ci hiVi hi .
vk h
h
2 xk
2 xk c p xk xk
xk i
cp
xk
2
i
Подставляя ; h h h ; vk vk vk ; vi vi vi ; ci ci ci ; ik ik ik ; и
пренебрегая корреляциями третьего порядка, и всеми теми корреляциями, которыми мы
уже пренебрегали ранее, получим
vi2
h
vk vk h
h vk
vi vi vk
vi ik
c x
x
xk
2
x
x
k p
k
k
k
ci
k
ci hi Vi c hi x .
xk i
p
k
ci
ci
ci ~
~ 0; ~ ~ D ~ 0; ci hi ~ 0; T ~ ciT ~ ci ~ ciT ~ 0; hi
xk
xk
Мы учли тот факт, что
Рассмотрим член h vk ci hi vk hi ci vk
h ci hi ; h ci hi hi ci ; hi c piT (корреляцией ci hi мы пренебрегаем).
Рассмотрим теперь первый член в выражении для h vk
ci hi vk ci c pi T vk c p T vk
19

20.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Осреднение уравнения энергии
По физическому смыслу этот член определяет дополнительный перенос тепла, из-за
пульсаций скорости. Мы назовем его турбулентным потоком тепла. Аналогично
предыдущему можно формально ввести турбулентный коэффициент теплопроводности:
c p T vk
k
k T
c p T vk T
или T T
xk
xk
Турбулентный поток тепла удобнее представить не через производную от осредненной
температуры, а через производную от осредненной энтальпии:
c
T
h
c p T vk T k
T
hi i
xk
c p xk
xk
Рассмотрим теперь второй член в выражении для h vk т.е. hi ci vk
k c1
v
c
D
Так как,
, поэтому hi ci vk DT k hi ci DT k h1 h2 c1
k 1
T
xk
xk
xk
для бинарного потока. Итак,
2
2
T k h T k
v
v
ci
i
i
vk vk h
h
v
v
v
v
xk c p xk xk c p i xk xk i i k xk i ik
xk
2
2
2
ci
k
k ci
v
DT hi
, где i 0, c h V k D k h ci .
ci hi Vi hi
i i i
T
i
xk i
c p xk xk
xk
2
20 xk

21.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Перейдем к пограничному слою для двухмерного течения, производя оценки порядков
величин так, как это было сделано при выводе уравнений динамического турбулентного
пограничного слоя:
H
H
h
1 c1
vx
v y v y
DT h1 h2 1
x
y
y c p xk
Le y
v x
T h
1 c1
DT h1 h2 1
,
T v x
y c p xk
Le
y
y
y
T
Le T
где
DT c p
- турбулентное число Льюиса.
T
Можно ввести еще турбулентное число Прандтля:
Pr
T c p
PrД .T . T
Le T T
PrT
DT
PrД .T
T
v x2
Заменяя h H
, получим:
vx
2
H
H
H
1 c
v y v y
D h1 h2 1 1
x
y y c p y
Le y
v x
v x
T H
1 c1
1
1
D
h
h
1
1
v
1
v
T 1
2
y y Pr x y y Pr T x y ,
y c p xk
Le
T
T
21

22.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Осреднение уравнений движения вязкой жидкости
Перегруппировав члены в уравнении энергии, систему уравнений можно записать:
Система уравнений
vx
v y v y 0.
x
y
vx
vx
vx
vx
vx
p
v
v
;
vx
v y v y
T
;
x y
T
y
y
x
y
x y
y
p v y2 const p ;
.
c1
c1
k c1
vx
v y v y
D DT M 1;
x
y y
y
vx
H
H
H
1 c
1 c1
v y v y
T
D h1 h2 1 1 DT h1 h2 1
x
y y Pr PrT y
Le
y
Le
T y
vx
vx q T H D h h 1 1 c1 .
1
1
1
2
T vx
1 vx
1
Pr Pr y
;
y
Le y y 0
T
y Pr
y y PrT
y
Проведенные к настоящему времени экспериментальные исследования профилей
скорости, профилей энтальпии и профилей концентраций в турбулентном
пограничном слое позволяют оценить значения Рrт, Leт. Оказывается, что в среднем
Рrт ~ 1 и Leт ~ 1 для пограничных слоев на поверхности твердых тел (для
свободных струй, однако Рrт≈0,5)
22