Похожие презентации:
Конвективный теплообмен. (Лекция 10)
1.
Лекции по ТТМОдоцент каф. Э6, ктн Рыжков С.В.
Э6
нергомашиностроение.
Лекция №10
ОСНОВНЫЕ ПОЛОЖЕНИЯ УЧЕНИЯ
О КОНВЕКТИВНОМ ТЕПЛООБМЕНЕ
•Основные понятия и определения
•Дифференциальное уравнение теории конвективного теплообмена
•Условия однозначности для процессов конвективного теплообмена
2.
Основные понятия и определенияКонвективным теплообменом называется передача теплоты при движении жидкости. В реальных
условиях конвекция теплоты всегда сопровождается молекулярным переносом теплоты, а иногда и
лучистым теплообменом.
Конвективный теплообмен между движущейся средой и поверхностью ее раздела с другой средой
(твердым телом, жидкостью или газом) называется теплоотдачей.
Конвективный теплообмен при движении жидкости под действием неоднородного поля массовых
сил (гравитационного, магнитного, электрического) называется свободной конвекцией.
Конвективный теплообмен при движении жидкости под действием внешних сил, приложенных на
границах системы, или однородного поля массовых сил, приложенных к жидкости внутри системы,
или за счет кинетической энергии, сообщенной жидкости вне системы, называется вынужденной
конвекцией.
Процесс теплоотдачи называется стационарным, если поле температур в жидкости не зависит от
времени, и нестационарным, если распределение температур в потоке зависит от времени.
qст ж
Т
n
(1)
n 0
qст (Т ж Т ст )
где
(2)
– коэффициент теплоотдачи.
ж
Т ж Т ст
Т
n
(3)
n 0
3.
Ниже приведен порядок значений коэффициента теплоотдачи для различныхусловий конвективного теплообмена, Вт/(м2К):
Свободная гравитационная конвекция в газах
Свободная конвекция воды
Вынужденная конвекция газов
Вынужденная конвекция воды
Кипение воды
Жидкие металлы
Пленочная конденсация водяных паров
Капельная конденсация водяных наров
5 — 30
102 — 103
10 — 500
500 — 2•104
2•103 — 5•105
102 — 3•104
4•103 — 1,5•104
4•104 —1,2•105
Значение коэффициента теплоотдачи зависит от:
1) причины движения жидкости (естественная или вынужденная конвекция)
2) режима течения жидкости(ламинарный или турбулентный)
3) скорости жидкости, теплофизических параметры жидкости, геометрической формы и размеров тела,
наличия фазовых переходов.
Обычно температура жидкости в условиях теплоотдачи изменяется от Тж до Тст в некоторой области,
называемой пограничным слоем.
Т
n
(Т ж Т ст )
Т
n 0
где δT – толщина теплового пограничного слоя.
ж
Т ж Т ст
Т
n
n 0
ж
Т
(4)
(5)
4.
Удельные плотности тепловых потоков различных источников теплоты, с которыми приходится иметь делов современной технике, приведены ниже, Вт/м2:
Тепловое излучение Солнца перпендикулярно поверхности Земли в полдень
Теплообменники на электростанциях
Реактивные двигатели на химическом топливе
Излучение поверхности Солнца
Тепловой поток к головной части спускаемых космических
аппаратов (скорость 11 км/с, масса 10т)
Реактивные двигатели на ядерном горючем
Термоядерные реактивные двигатели
Лазерное излучение
1,4 • 103
5 • 106
7 • 107
7,4 • 107
2 • 108
6 • 108
109
1012 -1020
Современная теория конвективного теплообмена базируется на
следующих основных предпосылках:
1) движущая среда, используемая для переноса теплоты,
рассматривается как сплошная среда;
2) система дифференциальных уравнений, описывающая
процессы конвективного теплообмена, выводится на основе ба
лансовых уравнений сохранения энергии, вещества и количества
движения;
3) для замыкания исходной системы дифференциальных
уравнений используются гипотезы, устанавливающие связь меж
ду тепловым потоком и градиентом температур, а также между
трением и градиентом скоростей;
ж
4) физические параметры жидкости (вязкость µж, плотность
теплоемкость срж и теплопроводность λж) считаются извест
ными функциями параметров состояния.
Рис. 1. Схема охлаждения лопатки газовой турбины
авиационного двигателя
5.
Дифференциальные уравнения теории конвективного теплообменаЗакон сохранения для движущейся среды
Первое начало термодинамики для элементарного объема движущейся среды можно записать в виде
w2
(6)
QV d LV d ( du d (
))
2
- количество теплоты, поступающей в единицу объема в единицу времени, Вт/м3; L - работа,
где QV
V
3
совершаемая внешними силами над единицей объема среды в единицу времени, Вт/м ; τ - время, с;
р - плотность среды, кг/м3; и - удельная внутренняя энергия, Дж/кг; w - скорость движения среды, м/с.
du dh d ( p )
(7)
где h - энтальпия, Дж/кг; р - давление, Па; v - удельный объем, м3/кг.
w2
w2
du d
dh d
dp pd
2
2
QV dV qdF qV dV (9) qdF div (q)dV
V
F
V
F
(8)
(10)
V
где qV - интенсивность внутренних источников теплоты (таких, как объемные химические реакции,
радиоактивный распад, работа трения и т.п.), Вт/м3.
QV divq qV 0
QV div( gradТ ) qV
(11)
(12)
6.
dpdv
dh d ( w2 / 2)
div( gradТ ) qV LV
p
(
)
d
d
d
d
Dh
div( gradТ ) qV
D
(13)
(14)
где Dh/Dτ - субстанциональная производная
Dh h
( w, grad h)
(15)
D
DT
с
2T qV
(16)
D
Т
Т
Т
Т
2Т 2Т 2Т
с (
wx
wy
wz
) ( 2
) qV (17)
2
2
x
y
z
x
y
z
Для неподвижной среды
T
с
2T qV
(18)
При отсутствии внутренних источников теплоты из уравнения (16) имеем
Т
( w, gradT ) a 2T
(19)
7.
Закон сохранения вещества для потока жидкостиЗакон сохранения массы жидкости М в произвольном объеме V, ограниченном поверхностью F,
можно записать в виде
dM F dM
(20)
Введем вектор плотности потока массы m
dM F d div mdV
V
d
dM d dV d dV
d
V
V
d
d
(23)
div m 0
(
div
m
)
dV
0
V d
d
m w
(21)
(22)
(24)
(25)
Уравнение неразрывности
d
div ( w) 0
d
(26)
8.
В прямоугольных координатахd
( wx ) ( w y ) ( wz ) 0
d x
y
z
Для плоского течения
d
( wx ) ( w y ) 0
d x
y
Для осесимметричного течения
d 1
1
(( rw x )
( rwr )) 0
d r x
r r
(27)
(28)
(29)
Для несжимаемой жидкости ρ = const и уравнение неразрывности имеет вид
div (w) 0
wx w y wz
0
x
y
z
(30)
(31)
9.
Закон сохранения количества движения вязкой жидкостиГлавный вектор количества движения жидкости, находящейся в объеме V
K wdV
(32)
V
DK
D
wdV M dV pdF
D D V
V
F
D
Dw
D
wdV
dV w
( dV )
D V
D
D
V
V
pdF div pdV
F
(33)
(34)
(35)
V
Dw
V ( D M div p)dV 0
Dw
M div p
D
Dw w
( w, grad w)
D
(36)
(37)
(38)
10.
w( w, grad w) M div p
pxx p yx pzx
( wx wy wz ) wx M x
x
y
z
x
y
z
(39)
pxy p yy pzy
( wx wy wz ) wy M y
(40)
x
y
z
x
y
z
pxz p yz pzz
( wx wy wz ) wz M z
x
y
z
x
y
z
В соответствии с гипотезой Ньютона касательное напряжение (напряжение сдвига) в плоском потоке вязкой
жидкости связано с производной от скорости по нормали к направлению потока простым соотношением
dwx
p xy xz
dy
(41)
Динамическая вязкость газа в зависимости от температуры достаточно удовлетворительно описывается
формулой Сазерленда
3
T 2
C
T 114
(42)
11.
Для воздуха3
T 2
14,65
T 114
(43)
Для практических расчетов можно использовать степенную зависимость
/ 0 ( T T ) n
(44)
0
Обобщенный закон Ньютона представляет линейную зависимость напряжений от скорости деформации
wi w j
( x x ) при j i
j
i
(45)
pij
p 2 wi при j i
xi
Здесь р - давление жидкости в любой точке потока; координаты х, у, z обозначены через х , (i = 1, 2, 3)
соответственно.
Жидкость, подчиняющаяся закону Ньютона, называется ньютоновской жидкостью.
Уравнение движения ньютоновской жидкости в векторной форме имеет вид
.
w
2
g 2div( S ) grad ( p divw)
y
3
i
(46)
12.
Здесь Dw/Dτ - вектор с проекциями Dwx/Dτ , Dwv/Dτ , Dwz/Dτ ; S - тензор скоростей деформаций,компонентами которого являются
wx
x
1 wy wx
2 x
y
1 wz wx
2 x
z
1 wx wy
2 y
x
wy
1 wx wz
2 z
x
y
1 wy wz
2 z
y
1 wx wy
2 y
z
wz
z
(47)
В проекциях на прямоугольную систему координат векторное уравнение (46) запишется в виде трех
уравнений, которые называются уравнениями Навье-Стокса:
Dwx
p
w
2 x
D
x
x x
Dwy
D
wx wy wx wz 2
div w g x
y
y
x
z
z
x
3
x
p wy wx
wy
2
y x x
y
y y
wy wz 2
div w g y
y 3 y
z z
Dwz
p wz wx wz wy
wz
2
D
z x x
z y y
z
z z
2
div w g z
3 z
(48)
Для изотермического течения несжимаемой жидкости ( = const) и (µ = const)
Dw
g grad p 2 w
D
(49)
13.
В проекциях на прямоугольные оси координат будем иметь1 p
2
w
w
w
w
g
wx
x
y
z
x
x
x
y
z
x
1 p
2
w
w
w
w
g
wy
x
y
z
y
y
x
y
z
y
(50)
1 p
2
w
w
w
w
g
wz
x
y
z
z
z
x
y
z
z
Проекция уравнения движения на ось Ох в цилиндрических координатах запишется в виде
2 w x 1 w x
1 p
wx
wy
wz wx g x
2
x
y
z
x
r
r
r
(51)
14.
Дифференциальное уравнение переноса массыРассмотрим перенос массы данного вещества с плотностью ρк в движущейся среде.
Тогда во всем объеме V в единицу времени будет образовываться количество вещества, равное
j
Vk
dV
j dS div
(52)
V
k
S
jk
dV
k
div
j
j
Vk dV 0
V
Vk
k
div jk jVk 0
jkM k w
jkM K1 k K 2 T
jk
(53)
(54)
(55)
(56)
(57)
где К1 и К2 - постоянные коэффициенты
k
k
k
k
k
p ,
T
T k , p
p k ,T
k p ,T
где
k /
(58)
15.
Введем следующие обозначения для коэффициента диффузии, термодиффузионного коэффициента ибародиффузионного отношения соответственно:
k
D K1
k p ,T
1
T
k
KT
K 2 K1
D
T к , p
k
p
Kp
K1
D p к ,T
jkM
K
D( k T
T
T K p p )
p
(59)
Первый член в правой части этого уравнения характеризует молекулярный перенос массы k-ой компоне
под действием градиента концентраций (закон диффузии Фика), второй определяет перенос массы
вследствие термодиффузии (эффект Соре), а третий характеризует бародиффузию (диффузию массы п
влиянием градиента общего давления). В большинстве случаев термодиффузией и бародиффузией мож
пренебречь и ограничиться законом Фика
jkM D k
(60)
16.
kw, grad k D 2 k jVk
(61)
В декартовых и в цилиндрических координатах уравнения имеет вид соответственно:
2 k 2 k 2 k
k
k
k
k
wx
wy
wz
D 2 2 2
x
y
z
y
z
x
jVk (62)
2 k 1 2 (r k )
k
k 1
(r k )
wx
wr
D 2
jVk
2
x r
r
r r
x
(63)
Уравнение диффузии типа (61) следует записать для каждой компоненты смеси. Общее количество
уравнений диффузии на единицу меньше числа компонент смеси, так как для массовых долей компоне
смеси имеется еще одно дополнительное условие
n
k 1
k
1
(64)
17.
Система уравнений для турбулентного движения жидкостиИз гидродинамики известно, что существуют два режима течения жидкости: ламинарный и
турбулентный. При ламинарном течении частицы жидкости следуют в потоке по вполне
определенным главным траекториям, все время сохраняя движение в направлении вектора средней
скорости потока, а возникающие в потоке случайные нерегулярности не развиваются, а гаснут. При
турбулентном течении в потоке возникают пульсации скорости, отдельные объемы жидкости
начинают двигаться поперек потока, причем эти объемы существенно больше тех, к которым можно
применить понятие дифференциального объема сплошной среды. Следовательно, общие уравнения
гидродинамики применимы и к турбулентному течению.
Турбулентное течение, строго говоря, является нестационарным, однако если осредненные по
времени скорости не изменяются или изменяются медленно, то действительную скорость можно
представить в виде суммы
w w
(65)
где w вектор осредненной скорости в данной точке;
вектор пульсационной составляющей истинной скорости,
дающий отклонение скорости по величене и направлению от
осрдненного значения.
w
1
wd
d 0
(66)
(67)
18.
Для вывода уравнений осредненного движения турбулентного потока, следуя Рейнольдсу, примемследующие правила осреднения:
если
1
1
d , то
d
Фd 0
где Ф - пульсационная составляющая φ
Dwx
p
2 wx x2
y x
z x
D
x
y
z
x
Dwy
p
2 wy
x y y2
z y
D
y
y
z
x
Dwz
p
2 wz
x z
y z z2
D
z
y
z
x
wx wy wz
0
x
y
z
(68)
19.
Из уравнений видно, что пульсации скорости вызывают появление новых членов, стоящих в квадратныхскобках, аналогичных по смыслу членам вязкого трения. Эти члены называются турбулентными
напряжениями и характеризуют дополнительный перенос количества движения молярными объемами
жидкости, перемещающимися вследствие пульсаций скорости.
В частности, для плоского установившегося турбулентного потока, когда скорость w - функция только
поперечной координаты у, из уравнений (68) имеем
2
dp
d w d
2
x y 0
dx
dy
dy
(69)
Введем понятие турбулентного касательного напряжения
T x y T dw / dy
(70)
выражение для суммарных касательных напряжений
( T )dw / dy
(71)
T T
(72)
DT
a 2T qv /(c p ) div( V )
D
V
Турбулентная теплопроводность
T
dT / dy
(73)
20.
DTa div((1 T / ) grad T ) qv /(c p )
D
D k
Ddiv((1 DT / D) grad k ) jVk
D
(74)
(75)
где DT - коэффициент турбулентной диффузии.
Условия однозначности для процессов конвективного теплообмена
Геометрические условия определяют форму и размеры твердого тела, на поверхности которого
следует определить q или T, расположение поверхности нагрева в потоке жидкости.
Физические условия определяют численные значения физических условий жидкости , , , CP ,
а также внутренние источники теплоты в потоке жидкости.
Временные условия учитывают особенности протекания процесса по времени и задаются в виде
начального распределения температур и скоростей.
Граничные условия определяют условия на поверхностях теплообмена и на границах потока.
Горизонтальную составляющую скорости на поверхности нагрева обычно принимают равной нулю
(условие прилипания жидкости к стенке). Вертикальная составляющая скорости на поверхности
нагрева в общем случае может быть отличной от нуля заданной или искомой величиной.
Тепловые граничные условия обычно включают задание температуры на поверхности нагрева или
тепловых потоков.
Так же как и в теории теплопроводности, различают три способа задания тепловых граничных условий.
При граничном условии I рода заданным является распределение температуры на поверхности
теплообмена. При граничном условии II рода известным является распределение удельного
теплового потока на поверхности теплообмена.
Граничное условие III рода связывает температуру поверхности теплообмена с температурой
окружающей среды через заданное значение коэффициента теплоотдачи. Обычно это условие
записывается в виде
T
(Tст Tж )
ст
n ст
(76)
21. Контрольные вопросы
Основные понятия и определения
Закон сохранения для движущейся среды
Закон сохранения вещества для потока жидкости
Закон сохранения количества движения вязкой жидкости
Дифференциальное уравнение переноса массы
Система уравнений для турбулентного движения жидкости
Условия однозначности для процессов конвективного теплообмена
Ньютоновская жидкость
Формула Сазерленда







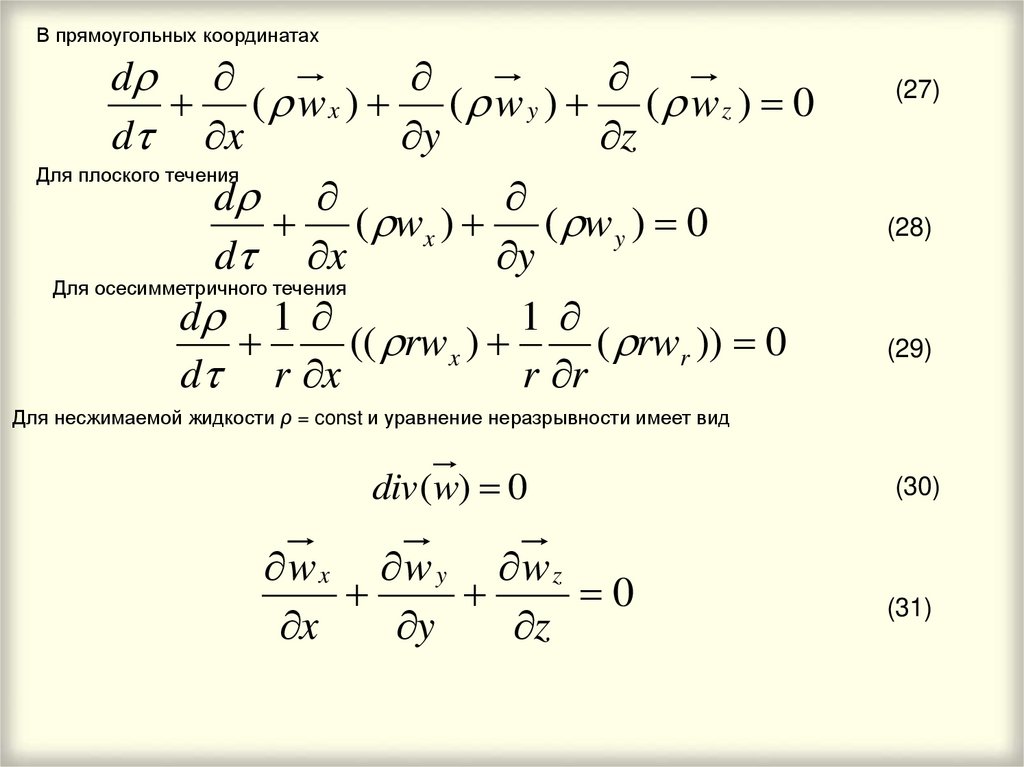













 Физика
Физика








