Лекция_24

1.

“Исследовательский Центр
имени М.В. Келдыша”
Теория теплообмена
Курс лекций В. Я. Лихушина
Лекция №23
Москва - 2007
1

2.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Закон убывания энтальпии на больших расстояниях от стенки
На больших расстояниях от стенки из числа параметров, определяющих h hw , следует
исключить , , c p , но учесть влияние :
функция от
qw , , y, w , или
функция от
qw , , y, w ,
значение осредненной энтальпии на внешней границе пограничного слоя.
На основании -теоремы теории размерностей, как и раньше, устанавливаем:
где функция g1, в отличие от функции f1 зависит от «предыстории» развития
(нарастания) пограничного слоя до рассматриваемого сечения (в частности, от
распределения статического давления р и энтальпии стенки hw ).
Предполагая, как и раньше, что на некотором участке при достаточно малых y , но в
пределах турбулентного ядра закон влияния стенки и закон убывания энтальпии должны
давать совпадающие значения энтальпии, получим, что при малых y закон убывания
энтальпии должен иметь вид:
2

3.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Закон убывания энтальпии на больших расстояниях от стенки
где константа С' от числа Прандтля не зависит, но зависит от характера развития
теплового пограничного слоя.
В пределах y , где законы влияния стенки и убывания энтальпии дают одинаковые
значения h , должно выполняться соотношение:
, откуда
h*
Подставляя
(где
закон турбулентного теплообмена:
qw
,
*
получаем
где
Аналогично тому, как это мы сделали в случае динамического пограничного слоя,
можно приближенно считать, что закон убывания энтальпии имеет вид:
подчинив при этом h и зависимости
*
или, прибегая к более грубому приближению, сделать то же самое, но принять, что С'~ 0.
Тогда:
3

4.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Закон убывания энтальпии на больших расстояниях от стенки
При таком приближенном представлении
закона убывания энтальпии получаются
достаточно точные значения энтальпии при
больших y вплоть до y 1 . В дальнейшем
полученный приближенный закон убывания
энтальпии и закон турбулентного теплообмена
мы получим и несколько другим путем.
Логарифмические законы турбулентного трения и теплообмена
Подведем итоги проведенного нами анализа структуры турбулентного пограничного
слоя. Как для динамического, так и теплового турбулентного пограничного слоя можно
использовать двухзонную модель течения в турбулентном пограничном слое. Обобщая
данные экспериментальных исследований, мы получили законы турбулентного трения и
турбулентного теплообмена в логарифмической форме.
Сейчас мы заново выведем эти законы, используя следующие результаты проведенного
анализа:
а) приближенные законы убывания скорости и убывания энтальпии;
б) экспериментальные данные, определяющие условия стыковки приближенных 4
законов убывания скорости и убывания энтальпии с линейными профилями скорости

5.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Логарифмические законы турбулентного трения и теплообмена
и энтальпии на условной внешней границе вязкого динамического подслоя и на
условной внешней границе вязкого теплового подслоя.
Рассмотрим отдельно динамический и тепловой пограничный слой.
Динамический пограничный слой
1. В пределах вязкого динамического подслоя вплоть до его условной внешней
границы:
Условия стыковки вязкого подслоя с логарифмическим слоем:
где в - толщина вязкого динамического подслоя;
vгв - значение осредненной скорости на условной внешней границе вязкого
динамического подслоя.
2. Приближенный логарифмический закон убывания скорости:
(напомним, что этот приближенный закон мы получили, положив С 0 и распространив
логарифмический профиль на область течения в пределах всего турбулентного ядра).
Заменяя
можно записать:
5

6.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Логарифмические законы турбулентного трения и теплообмена
Динамический пограничный слой
Для расстояния, соответствующего условиям внешней границы динамического вязкого
подслоя,
Подставляя условия стыковки, получаем закон
турбулентного трения:
или
В отличие от прежнего результата вместо константы (В + С) в соответствии со
сделанными упрощающими предположениями фигурирует величина
Зная v x U легко найти связь между Re и Re **:
Заменяя Re на
форме:
можем записать закон турбулентного трения в
6

7.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Логарифмические законы турбулентного трения и теплообмена
Тепловой пограничный слой
1. В пределах вязкого теплового подслоя вплоть до его условной внешней границы
Условия стыковки вязкого подслоя с логарифмическим слоем:
где в - толщина вязкого теплового подслоя;
hв - значение осредненной энтальпии при у = в .
2. Приближенный логарифмический закон убывания энтальпии:
(этот приближенный закон мы получили, положив С' 0 и распространив
логарифмический профиль на область течения в пределах всего турбулентного ядра).
Заменяя
можно записать:
7

8.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Логарифмические законы турбулентного трения и теплообмена
Тепловой пограничный слой
Для расстояния от стенки у = в:
Используя условия стыковки, получаем закон турбулентного теплообмена:
(заметим, что
Заменяя, как и раньше, Re на Re **
1
C f
C f
C f
y CH
y
y C
y y
1
ln
ln
dy 1
ln
ln H ln d
k
k C f
k
k
k C f
0
0
**
получим:
8

9.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Логарифмические законы турбулентного трения и теплообмена
Тепловой пограничный слой
Как мы уже отмечали, C'f и Сн можно аппроксимировать формулами:
Как показывают эксперименты, полученные
формулы справедливы в широком диапазоне
значений Re ** и Re ** при условии, однако, что
Re ** и Re ** не сильно отличаются друг от друга.
9

10.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Исходя из формальной аналогии между турбулентными пульсациями и тепловым
движением молекул, Прандтль ввел понятие о длине пути перемешивания.
При рассмотрении явлений обмена количеством движения между частицами газа или
жидкости (молями) можно формально ввести понятие о длине l' как о расстоянии, на
протяжении которого данная частица жидкости или газа движется без изменения своего
количества движения.
При рассмотрении явлений обмена энергией (теплом) между частицами газа или
жидкости (молями) можно формально ввести понятие о длине l как о расстоянии, на
протяжении которого данная частица жидкости или газа движется не обмениваясь
энергией (теплом) с соседними частицами.
Представления о длине пути перемешивания для обмена количеством движения и для
обмена энергией между движущимися молями являются, конечно, чисто качественными,
так как в действительности обмен количеством движения и энергией между
движущимися частицами происходит непрерывно. Тем не менее гипотеза Прандтля дает
возможность получить или, вернее, представить формулы для турбулентного напряжения
трения и турбулентного теплового потока в таком виде, который является очень удобным
для анализа экспериментальных данных, позволяет объединить их в рамках единой 10
простейшей модели турбулентного движения.

11.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Формула турбулентного трения Прандтля
Как известно,
T v x v y .
Используя идею о длине пути перемешивания l', можно положить, что пульсация
скорости v x равна изменению скорости осредненного движения vx на расстоянии по
нормали к стенке, равном l' :
v
v x vx y l vx y x l
y
[считая, что l' мало в сравнении с толщиной динамического пограничного слоя] (рис.
129). Опираясь на данные экспериментов, можно принять, что пульсация v y имеет тот же
порядок величины, что и v x
где а- коэффициент порядка единицы.
Рис. 129
11

12.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Формула турбулентного трения Прандтля T v x v y .
Заметим, что l' зависит не только от координаты у , но и от времени . Подставляя
значения v x и v y в формулу для т, получим l' :
(черточка над буквой, как всегда, означает осреднение по времени).
Положим
где l - среднее по времени значение эквивалентной длины пути перемешивания для
процессов обмена количеством движения между молями.
Для абсолютного значения турбулентного напряжения трения получаем формулу
Прандтля:
Значение длины пути перемешивания l, входящей в формулу Прандтля, может быть
строго определено, только для достаточно малых расстояний от стенки, в пределах
которых т>> , а т w и профиль скорости имеет логарифмический характер:
В этом случае, как мы уже знаем,
Откуда l = ky (k - экспериментальная константа, k ≈ 0,4 ). 12

13.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Формула турбулентного трения Прандтля
Для всего диапазона изменения координаты у (0 ≤ y ≤ ) зависимость l от у может
быть пока определена только из экспериментов.
Достаточно полные данные для определения функции l(у) имеются только для труб и
каналов. В этих случаях известны как эмпирические профили скоростей
так и зависимость напряжения трения от безразмерной координаты
v
T l x
y
2
2
Зная зависимость
l
0,16
и от координаты у, легко найдем:
l
y
0,4
Из рис. 130 видно, что зависимость
l
0,08
при малых y
0
Рис. 130
y
носит существенно нелинейный характер и только
y
0,5
l
от
1,0
l
y
k
13

14.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Формула турбулентного трения Прандтля
В общем случае
, где функция
линейной зависимости l = kу .
характеризует отклонение от
Подставляя в формулу Прандтля w, l, можно вновь получить профиль скорости
2
(именно тот, по которому определялось значение l(у)):
2 v
T l x
y
y
w 1
Эта формула справедлива только для турбулентного ядра. Интегрируя, получим:
- закон убывания скорости для турбулентного ядра
Как и следовало ожидать, закон убывания скорости отличается от
логарифмического закона убывания скорости:
14

15.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Формула турбулентного трения Прандтля
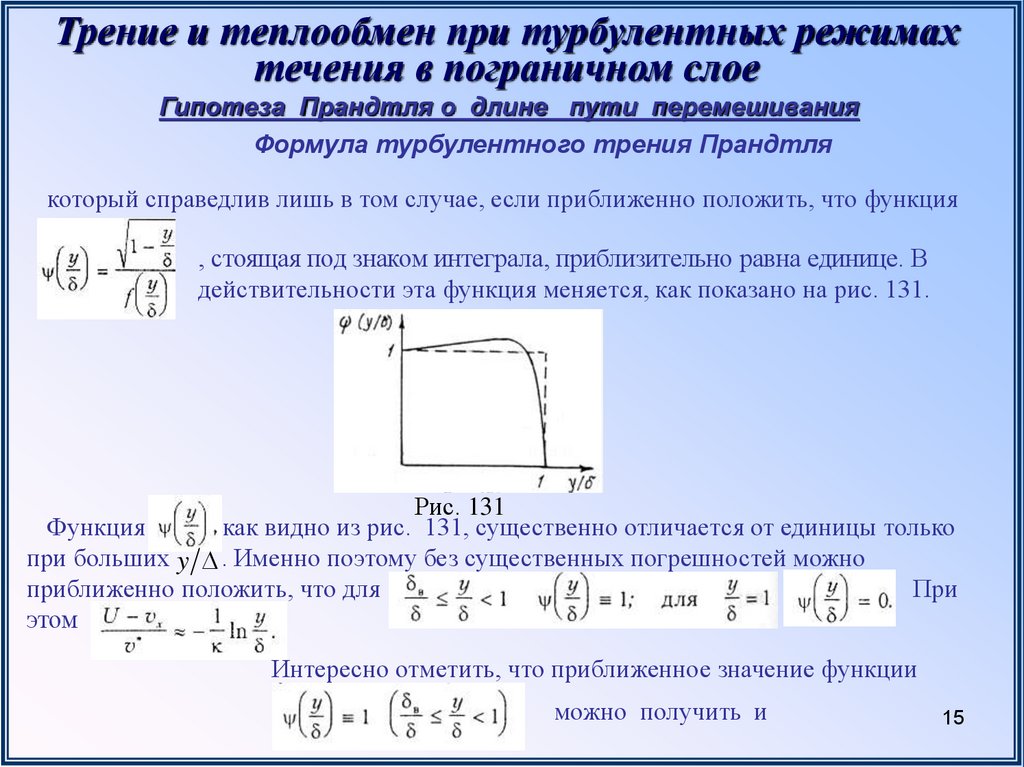
который справедлив лишь в том случае, если приближенно положить, что функция
, стоящая под знаком интеграла, приблизительно равна единице. В
действительности эта функция меняется, как показано на рис. 131.
Рис. 131
Функция
как видно из рис. 131, существенно отличается от единицы только
при больших y . Именно поэтому без существенных погрешностей можно
приближенно положить, что для
При
этом
Интересно отметить, что приближенное значение функции
можно получить и
15

16.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Формула турбулентного трения Прандтля
непосредственно, если одновременно ввести два грубых предположения:
Каждое из этих предположений, взятое отдельно, наверно, и дает неверное значение
. Но взятые вместе они дают приближенное значение
которое для
большей части турбулентного ядра не очень сильно отличается от точного значения.
Итак, используя формулу для турбулентного напряжения трения Прандтля, а также
результаты экспериментальных исследований турбулентного пограничного слоя в
трубах и каналах, мы можем получить приближенный логарифмический закон
убывания скорости. Распространяя этот результат и на случаи образования
турбулентного пограничного слоя при внешнем обтекании твердого тела, а также
используя эмпирические условия «стыковки» логарифмического профиля в
турбулентном ядре с линейным профилем скорости в пределах вязкого подслоя, мы
снова приходим к соотношениям, с помощью которых нами был получен
логарифмический закон турбулентного трения:
16

17.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Формула турбулентного трения Прандтля
Как и раньше, получаем:
17

18.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Тепловой пограничный слой.
Формула Прандтля для турбулентного теплового потока
Как известно, qT v y h (ограничиваемся случаем несжимаемых потоков).
Используя идеи о длине пути перемешивания l' для обмена количеством движения и
длине пути перемешивания lт' для обмена энергией, можем положить (рис. 132):
x
Рис. 132
Тогда
или, вводя среднее по времени
18

19.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Тепловой пограничный слой.
Формула Прандтля для турбулентного теплового потока
откуда
Замечая, что
находим
Окончательно можем записать формулу Прандтля для турбулентного теплового
потока в виде:
если рассматривать
абсолютные значения qт .
Для пограничного слоя на поверхности твердого тела
Для малых расстояний от стенки, когда qт ≈ qw, a т >> , т>> и профили
скорости и энтальпии имеют логарифмический характер, мы можем, как в случае
19
динамического пограничного слоя, получить точную зависимость l от у : l = ky.

20.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Тепловой пограничный слой.
Формула Прандтля для турбулентного теплового потока
Тогда
В общем случае, однако, как мы уже знаем,
v
T l x
y
2
2
Зная зависимость l от у, можно найти распределение энтальпии в турбулентном ядре
турбулентного теплового пограничного слоя, если известно распределение qт. Мы
используем, однако, приближенный прием, аналогичный тому, который мы применили
в случае динамического пограничного слоя. Положим
Интегрируя в турбулентном ядре от у до , получаем приближенный
логарифмический закон:
Присоединяя к приближенному логарифмическому закону убывания энтальпии
условия «стыковки» логарифмического закона с линейным законом изменения
энтальпии в пределах вязкого теплового пограничного слоя, получаем соотношения, из
которых так же, как и раньше, следует логарифмический закон турбулентного
20
теплообмена:

21.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Тепловой пограничный слой.
Формула Прандтля для турбулентного теплового потока
Как и раньше, получаем логарифмический закон турбулентного теплообмена:
21

22.

Трение и теплообмен при турбулентных режимах
течения в пограничном слое
Гипотеза Прандтля о длине пути перемешивания
Тепловой пограничный слой.
Формула Прандтля для турбулентного теплового потока
Законы турбулентного трения и турбулентного теплообмена мы в дальнейшем будем
условно записывать в форме:
Индекс log означает, что мы пользуемся логарифмическими законами.