Лабораторная работа 2

1.

Лабораторная работа 2

2.

Для моделирования внезапных отказов используют
экспоненциальный (показательный) закон распределения:
Экспоненциальный
закон

3.

• Основным признаком постепенного
отказа является монотонно возрастающий
характер зависимости интенсивности
отказов от наработки объекта:
Распределение
Релея
λ2(t2) > λ1(t1) при t2 > t1.
• Этому условию удовлетворяет,
например, нормальный закон
распределения или закон Рэлея. Внезапные
отказы характеризуются скачкообразным
характером зависимости степени
повреждения объекта от наработки при
t > Tв , где Tв время (наработка),
соответствующее возникновению.
Основным признаком внезапного отказа
является независимость интенсивности
отказов λ от наработки объекта (λ = const)
причины, вызывающей внезапный отказ.
• Интенсивность отказов λ выступает,
таким образом, как смешанная мера
интенсивности случайных внешних
воздействий, которым подвергается объект
при эксплуатации, и способности объекта
противостоять этим воздействиям.

4.

Закон
Вейбулла
При α = 1 распределение
превращается в экспоненциальное,
при α < 1 функции плотности и
интенсивности отказов убывающие
(период приработки системы),
при α > 1 интенсивность отказов
возрастающая (период старения
системы).
При α = 3,3 распределение
Вейбулла близко к нормальному,
а при α = 2 функция λ(t) линейная и
распределение Вейбулла
превращается в распределение
Рэлея

5.

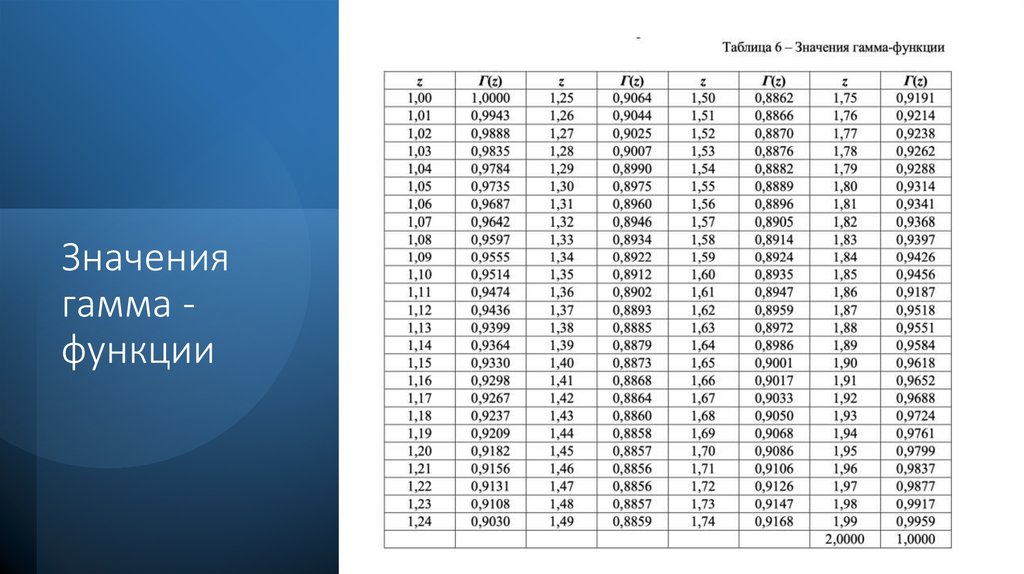
Гаммараспределение

6.

Значения
гамма функции

7.

Основные соотношения количественных характеристик надежности при
различных закзависимостЗззззонах распределения времени безотказной работы

8.

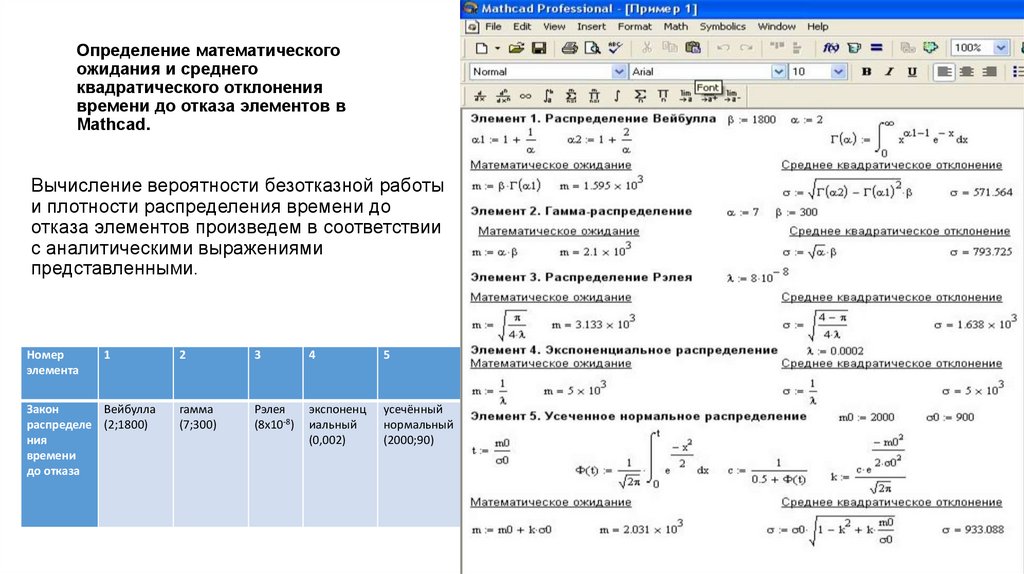
Определение математического
ожидания и среднего
квадратического отклонения
времени до отказа элементов в
Mathcad.
Вычисление вероятности безотказной работы
и плотности распределения времени до
отказа элементов произведем в соответствии
с аналитическими выражениями
представленными.
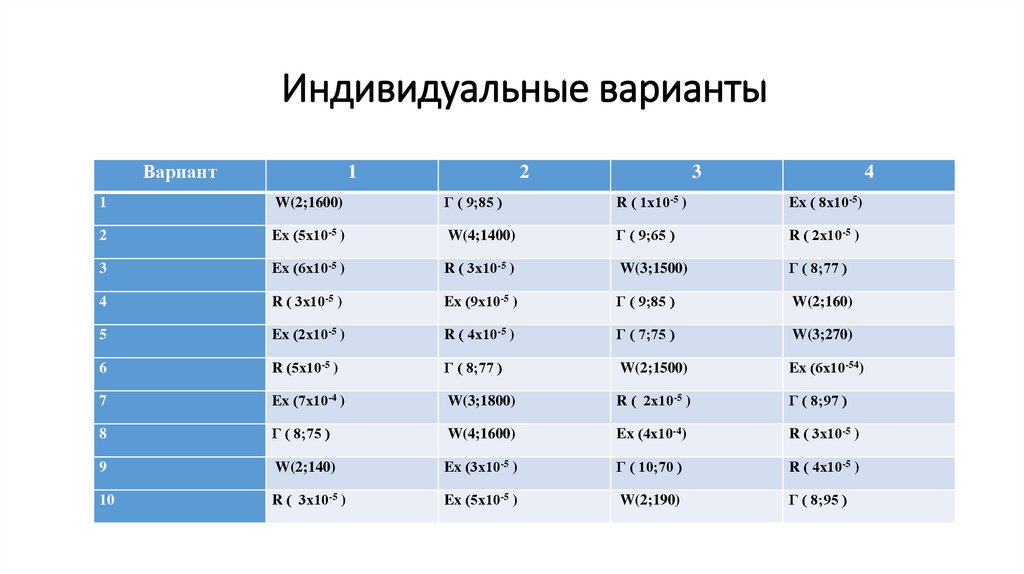
Номер
элемента
1
Закон
Вейбулла
распределе (2;1800)
ния
времени
до отказа
2
3
4
5
гамма
(7;300)
Рэлея
(8х10-8)
экспоненц
иальный
(0,002)
усечённый
нормальный
(2000;90)

9.

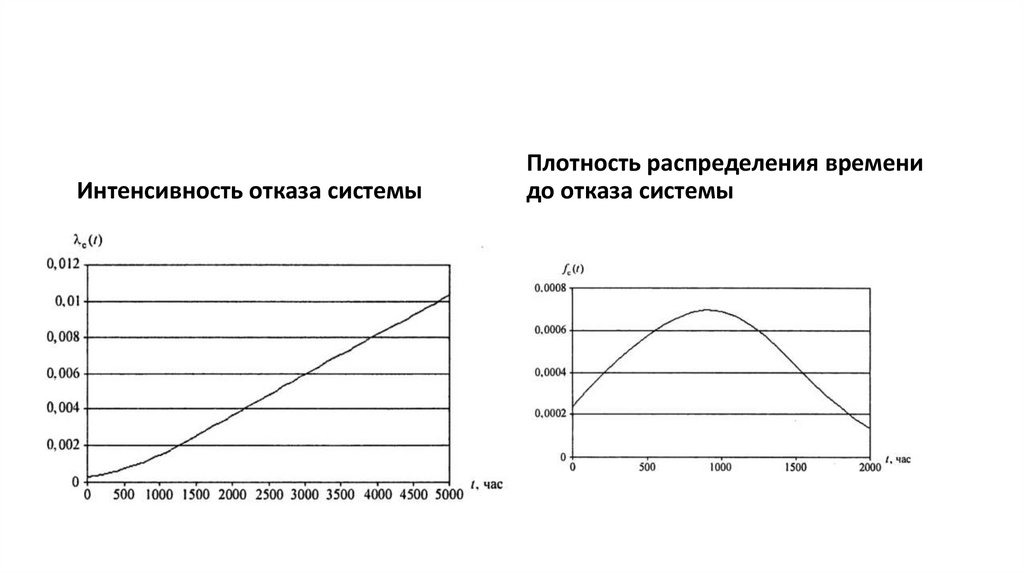
Вычисление
вероятности
безотказной работы
и плотности
распределения

10.

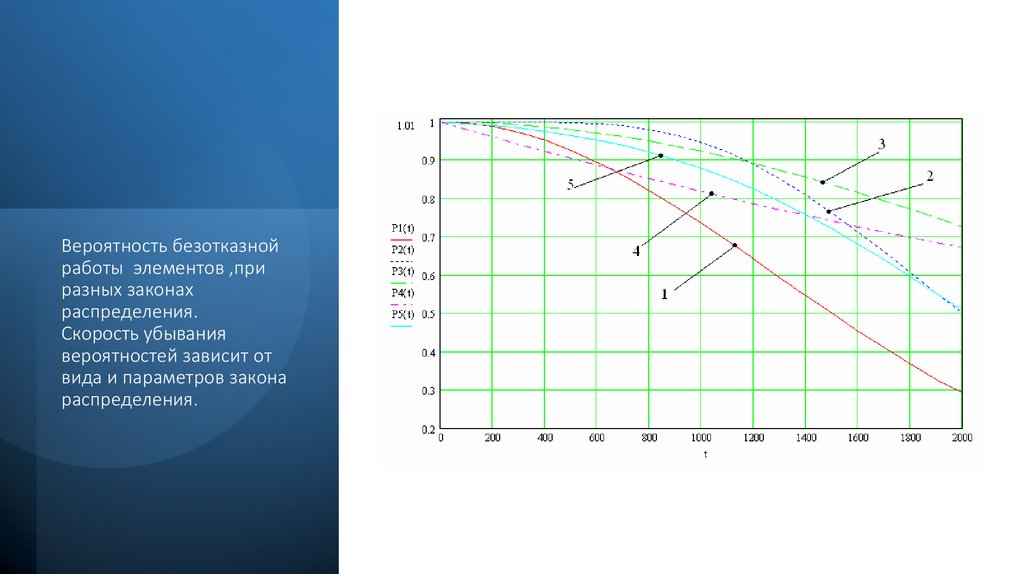
Вероятность безотказной
работы элементов ,при
разных законах
распределения.
Скорость убывания
вероятностей зависит от
вида и параметров закона
распределения.

11.

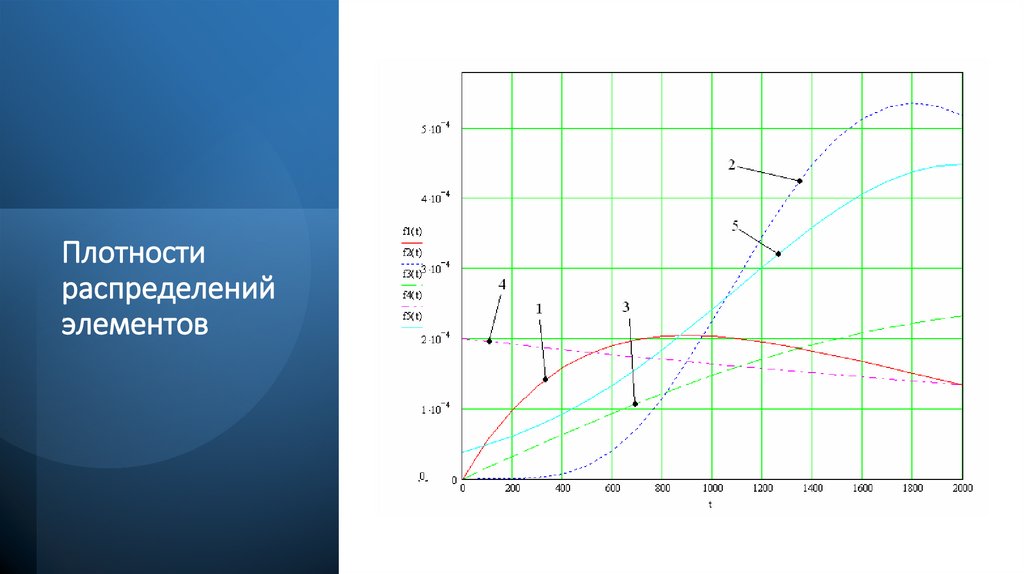
Плотности
распределений
элементов

12.

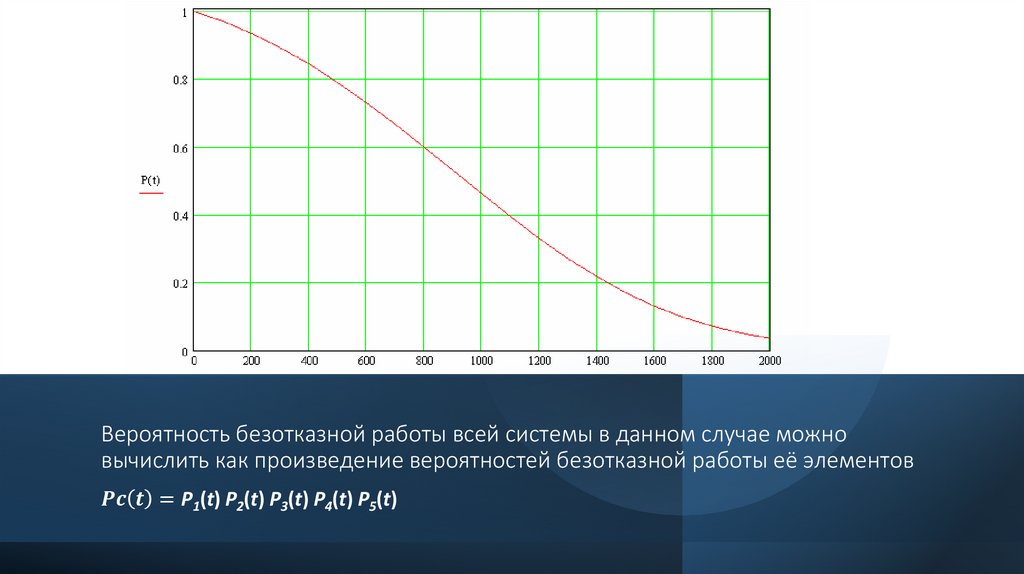
Вероятность безотказной работы всей системы в данном случае можно
вычислить как произведение вероятностей безотказной работы её элементов