Основные законы распределения

1. Основные законы распределения

2.

Экспоненциальное распределение
Этот закон описывает надежность
работы изделия в период его
нормальной эксплуатации, когда
постепенные отказы вследствие износа
и старения еще не проявляются и
надежность характеризуется
внезапными отказами.

3.

Внезапные отказы вызываются
неблагоприятным сочетанием
различных факторов и имеют
постоянную интенсивность
.

4.

Экспоненциальное распределение
наиболее применимо для оценки
безотказности объектов в период после
приработки и до проявления
постепенных отказов.
Этот закон используется также при
решении задач об обслуживании
сложных систем.

5.

Экспоненциальное распределение
имеет только один параметр λ и является частным случаем распределения
Вейбулла и гамма - распределения.

6.

Функция распределения случайной
величины при экспоненциальном законе
распределения
Функция распределения описывает вероятность
возникновения отказов объекта.

7.

Плотность вероятности
экспоненциального распределения

8.

Вероятность безотказной работы может
быть определена по формуле
где
– интенсивность отказов.

9.

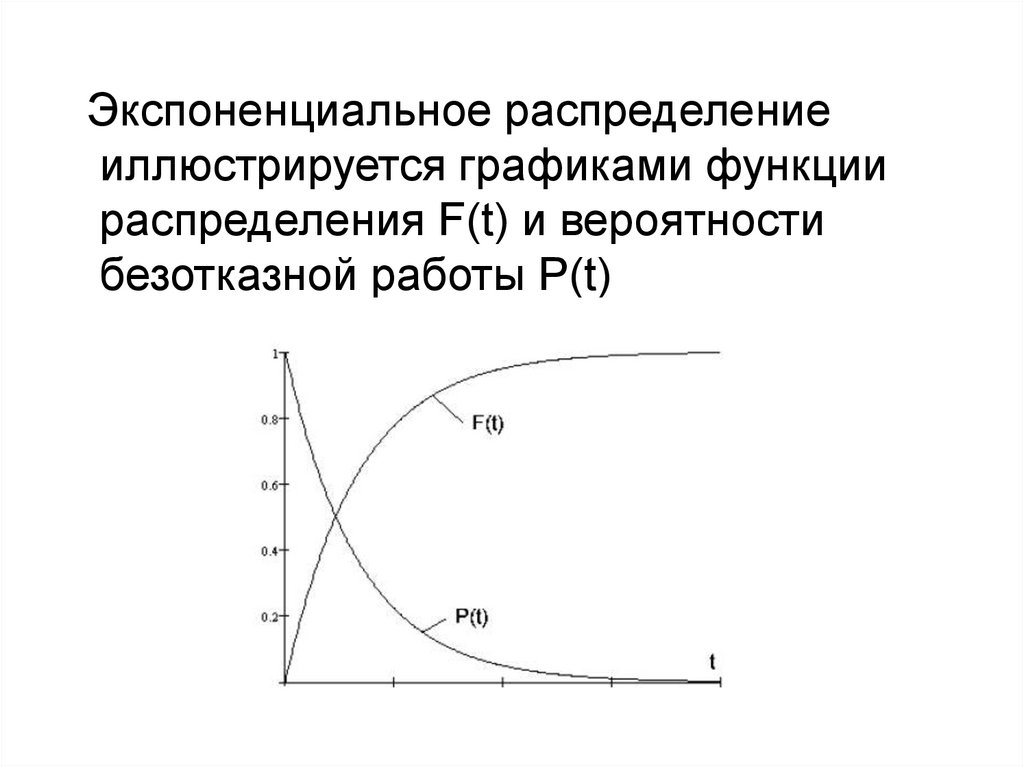
Экспоненциальное распределение
иллюстрируется графиками функции
распределения F(t) и вероятности
безотказной работы P(t)

10.

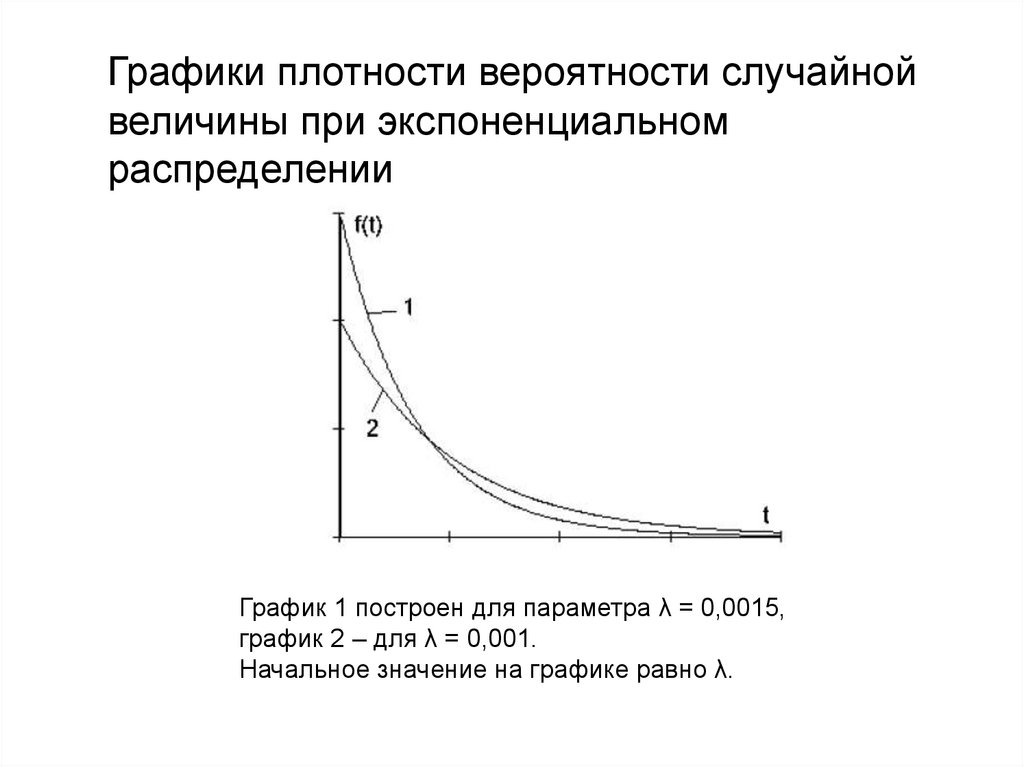
Графики плотности вероятности случайной
величины при экспоненциальном
распределении
График 1 построен для параметра λ = 0,0015,
график 2 – для λ = 0,001.
Начальное значение на графике равно λ.

11.

Математическое ожидание и среднее
квадратическое отклонение для
экспоненциального закона
равны между собой

12.

Равенство математического ожидания и
среднеквадратического отклонения для
экспоненциального закона
является существенным признаком для
отнесения экспериментального
распределения к теоретическому
экспоненциальному распределению.

13.

Распределение Вейбулла
Распределение Вейбулла является
двухпараметрическим универсальным
законом, так как при изменении
параметров оно может описывать
нормальное распределение,
логарифмически нормальное
распределение, экспоненциальное
распределение и др.

14.

Распределение Вейбулла
характеризуется параметром
масштаба λ и параметром
формы α.

15.

Функция распределения для закона
Вейбулла имеет вид
Функция надежности

16.

Плотность вероятности распределения
Вейбулла выражается зависимостью
Если для закона Вейбулла принять α = 1, то получим
экспоненциальное распределение, которое является
частным случаем распределения Вейбулла.

17.

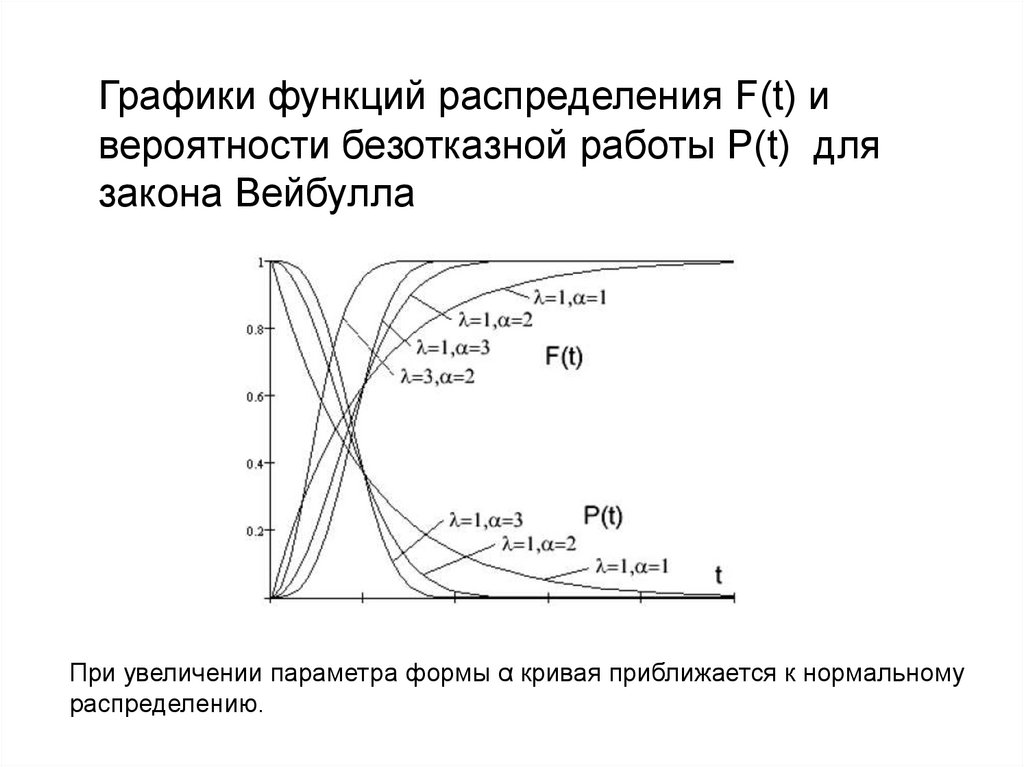
Графики функций распределения F(t) и
вероятности безотказной работы P(t) для
закона Вейбулла
При увеличении параметра формы α кривая приближается к нормальному
распределению.

18.

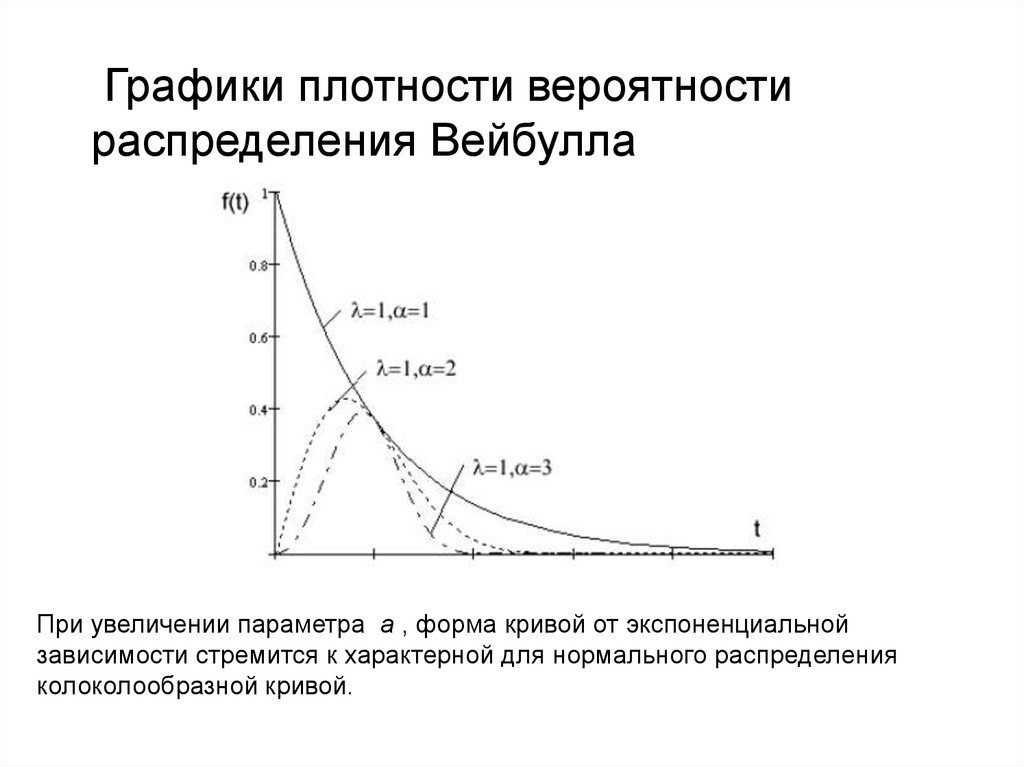
Графики плотности вероятности
распределения Вейбулла
При увеличении параметра а , форма кривой от экспоненциальной
зависимости стремится к характерной для нормального распределения
колоколообразной кривой.

19.

Гамма-распределение
Гамма-распределение характеризуется двумя
параметрами:
-λ – параметр масштаба
-α – параметр формы.
Гамма-распределение имеет ограничение с одной
стороны
Это распределение описывает наработку системы с
резервированием, время восстановления, а также
распределение постепенных отказов вследствие
износа.

20.

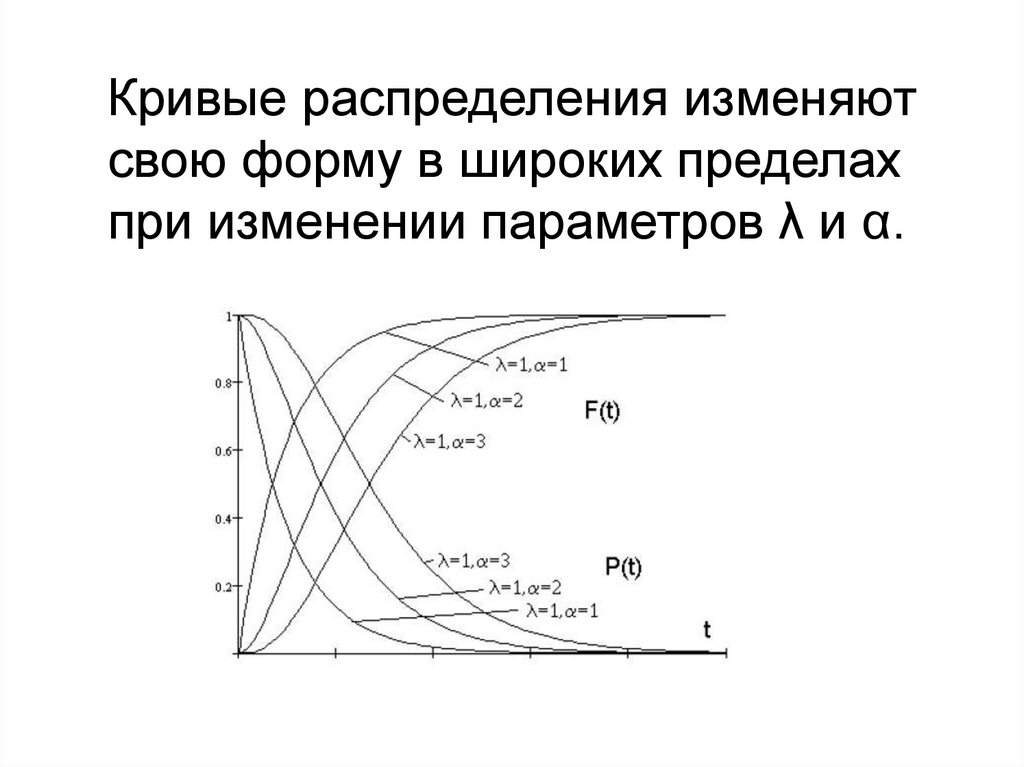
Кривые распределения изменяют
свою форму в широких пределах
при изменении параметров λ и α.

21.

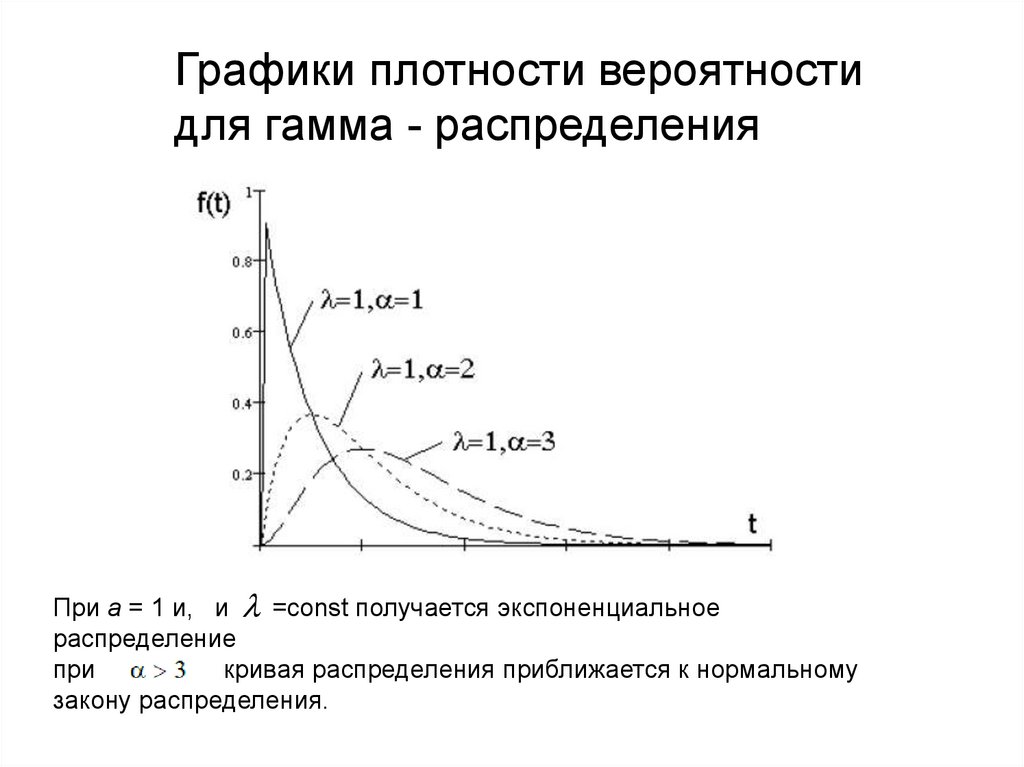
Графики плотности вероятности
для гамма - распределения
При а = 1 и, и =сonst получается экспоненциальное
распределение
при
кривая распределения приближается к нормальному
закону распределения.

22.

Математическое ожидание и дисперсия для
гамма-распределения