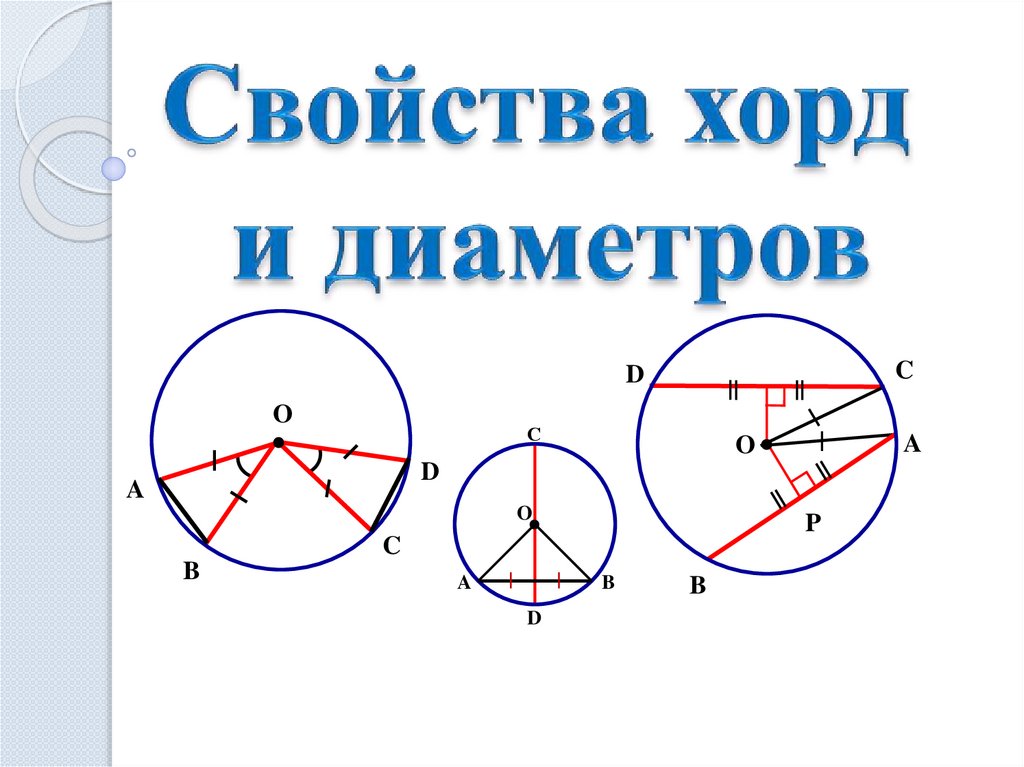
Своиства хорд и диаметров

1.

C
D
O
С
A
O
D
A
O
P
C
B
A
B
D
B

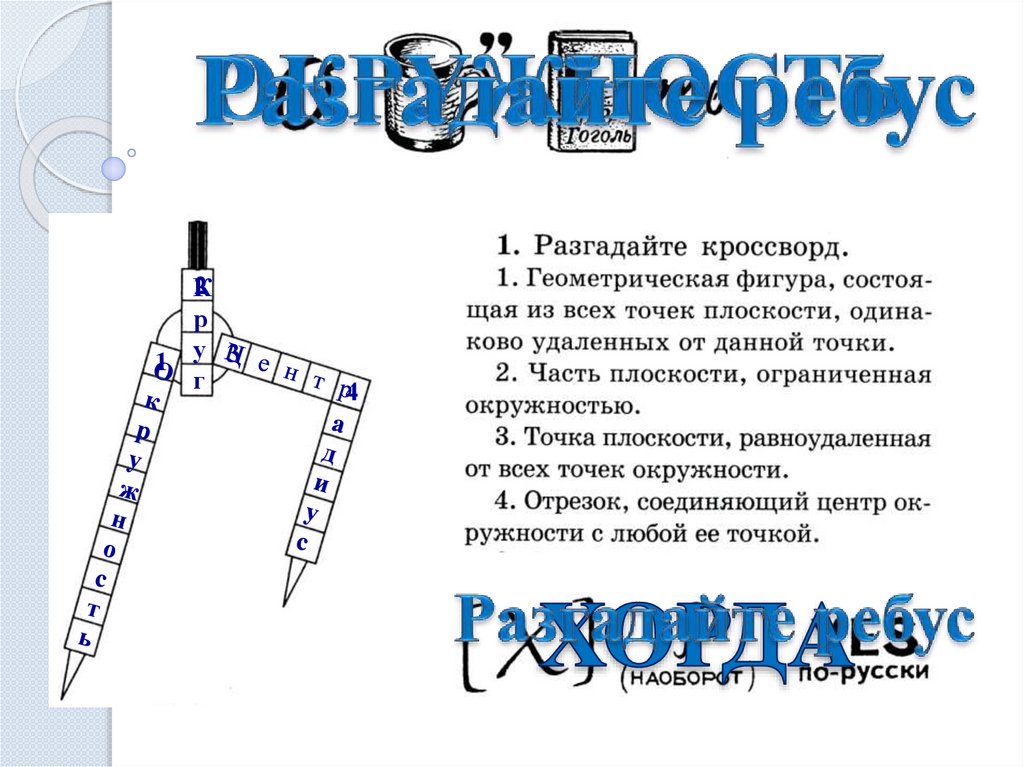
2.

2
К
р
1 у 3
г
4

3.

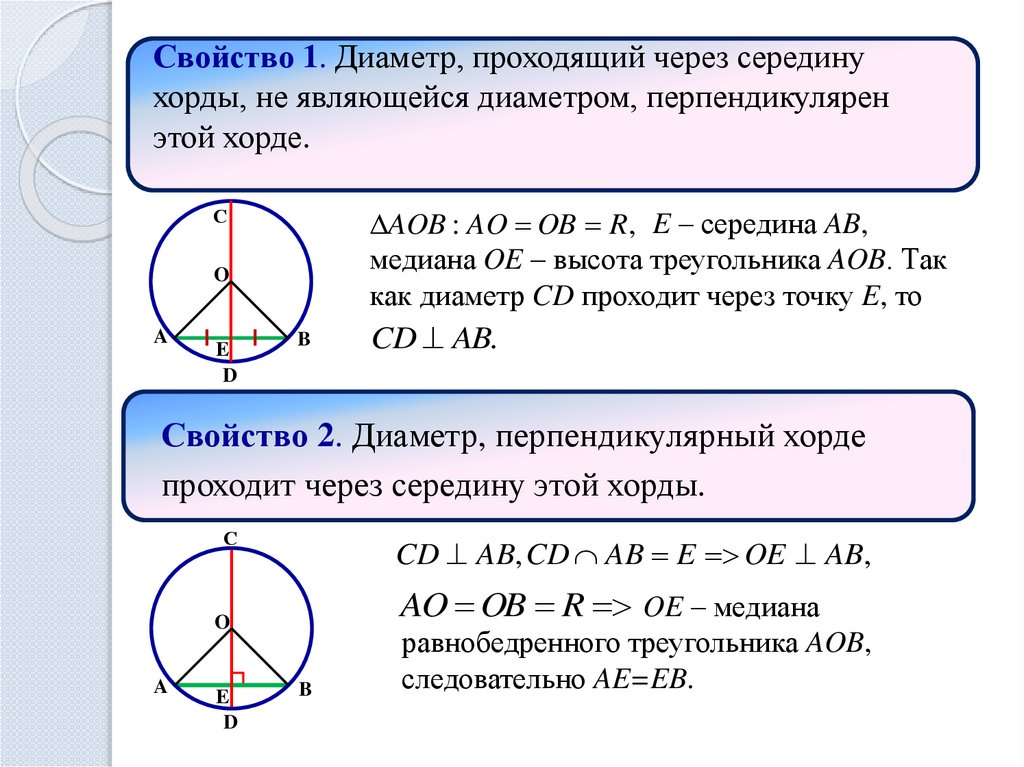
Свойство 1. Диаметр, проходящий через середину
хорды, не являющейся диаметром, перпендикулярен
этой хорде.
AOB : AO OB R, E – середина AB,
медиана OE – высота треугольника AOB. Так
как диаметр CD проходит через точку E, то
С
O
A
E
D
B
CD AB.
Свойство 2. Диаметр, перпендикулярный хорде
проходит через середину этой хорды.
С
CD AB, CD AB E OE AB,
AO OB R OE – медиана
O
A
E
D
B
равнобедренного треугольника AOB,
следовательно AE=EB.

4.

Вывод. Диаметр перпендикулярен хорде, не
являющейся диаметром, тогда и только тогда, когда
он проходит через её середину.
Расстояние от центра окружности до хорды равно
расстоянию от центра до середины этой хорды.

5.

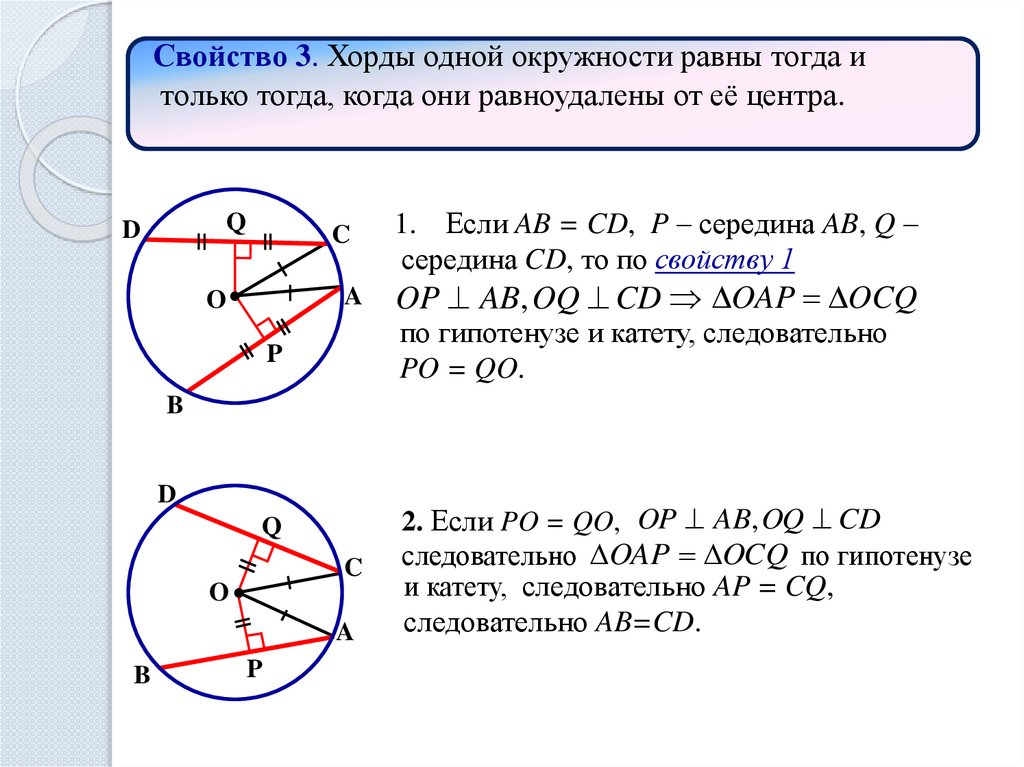
Свойство 3. Хорды одной окружности равны тогда и
только тогда, когда они равноудалены от её центра.
Q
D
C
A
O
1. Если AB = CD, P – середина AB, Q –
середина CD, то по свойству 1
OP AB, OQ CD OAP OCQ
по гипотенузе и катету, следовательно
PO = QO.
P
B
D
Q
C
O
A
B
P
2. Если PO = QO, OP AB, OQ CD
следовательно OAP OCQ по гипотенузе
и катету, следовательно AP = CQ,
следовательно AB=CD.

6.

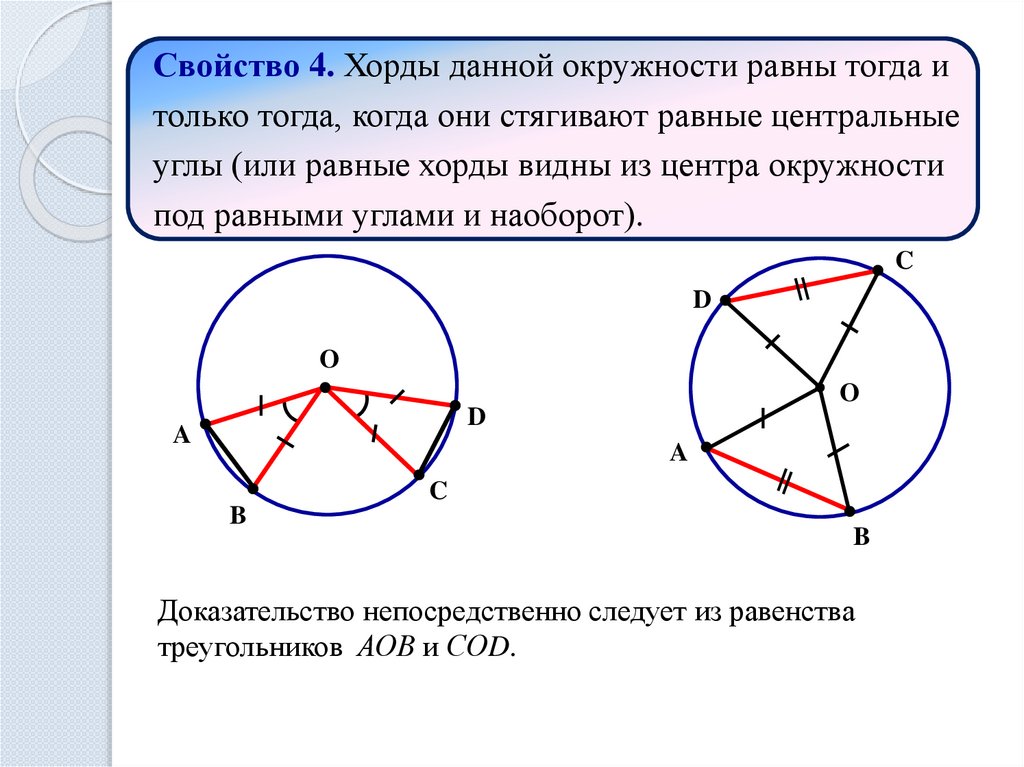
Свойство 4. Хорды данной окружности равны тогда и
только тогда, когда они стягивают равные центральные
углы (или равные хорды видны из центра окружности
под равными углами и наоборот).
C
D
O
O
D
A
A
C
B
B
Доказательство непосредственно следует из равенства
треугольников АОВ и СОD.

7.

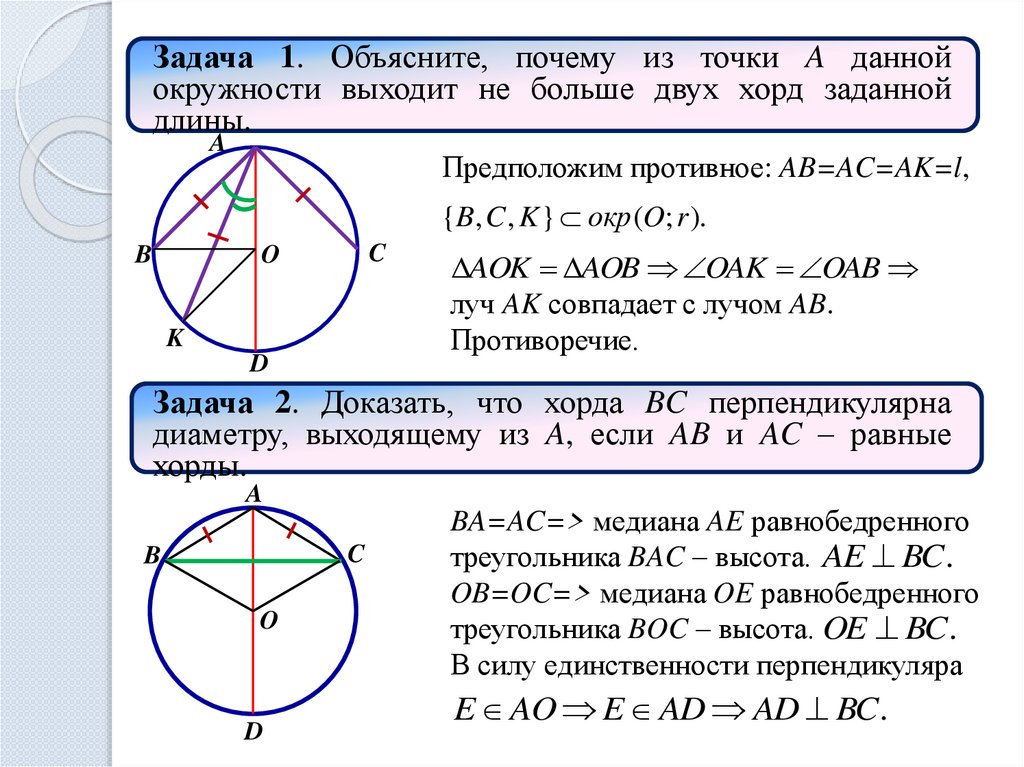
Задача 1. Объясните, почему из точки A данной
окружности выходит не больше двух хорд заданной
длины.
A
Предположим противное: AB=AC=AK=l,
{B, C , K } окр (O; r ).
C
O
B
K
D
AOK AOB OAK OAB
луч AK совпадает с лучом AB.
Противоречие.
Задача 2. Доказать, что хорда BC перпендикулярна
диаметру, выходящему из A, если AB и AC – равные
хорды.
A
C
B
O
D
BA=AC=> медиана AE равнобедренного
треугольника BAC – высота. AE BC.
OB=OC=> медиана OE равнобедренного
треугольника BOC – высота. OE BC.
В силу единственности перпендикуляра
E AO E AD AD BC.

8.

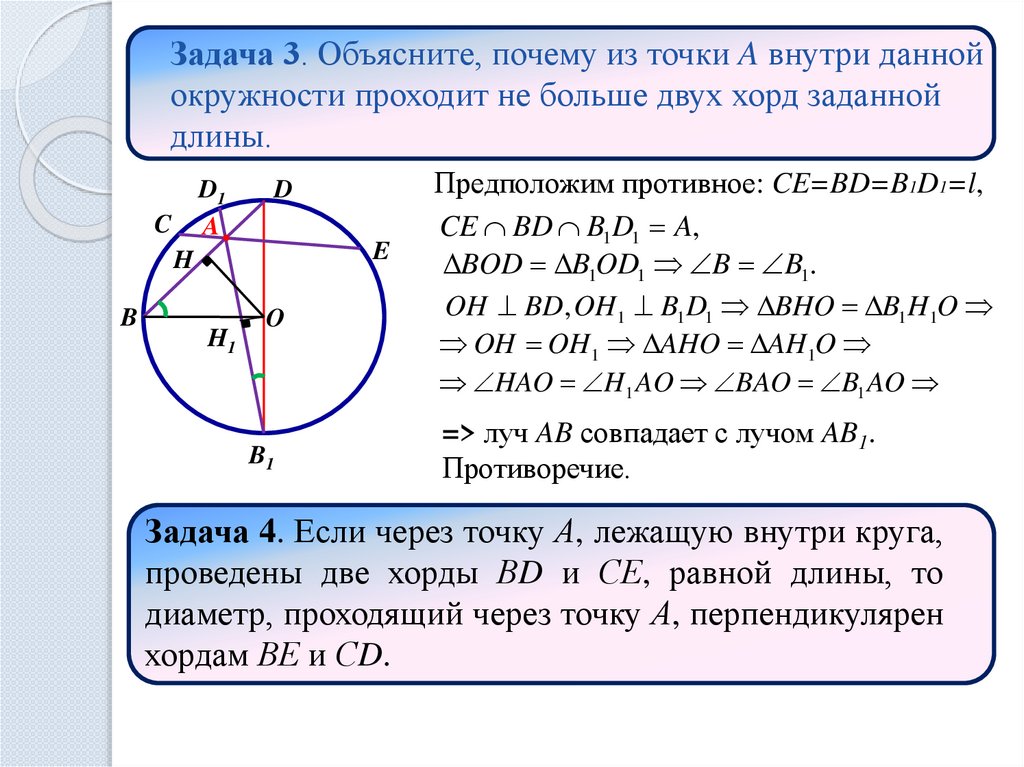
Задача 3. Объясните, почему из точки A внутри данной
окружности проходит не больше двух хорд заданной
длины.
D1
A.
C
D
D
E
H
B
H1
O
B1
Предположим противное: CE=BD=B1D1=l,
CE BD B1 D1 A,
BOD B1OD1 B B1.
OH BD, OH1 B1 D1 BHO B1 H1O
OH OH1 AHO AH1O
HAO H1 AO BAO B1 AO
=> луч AB совпадает с лучом AB1.
Противоречие.
Задача 4. Если через точку А, лежащую внутри круга,
проведены две хорды ВD и СЕ, равной длины, то
диаметр, проходящий через точку А, перпендикулярен
хордам ВЕ и СD.

9.

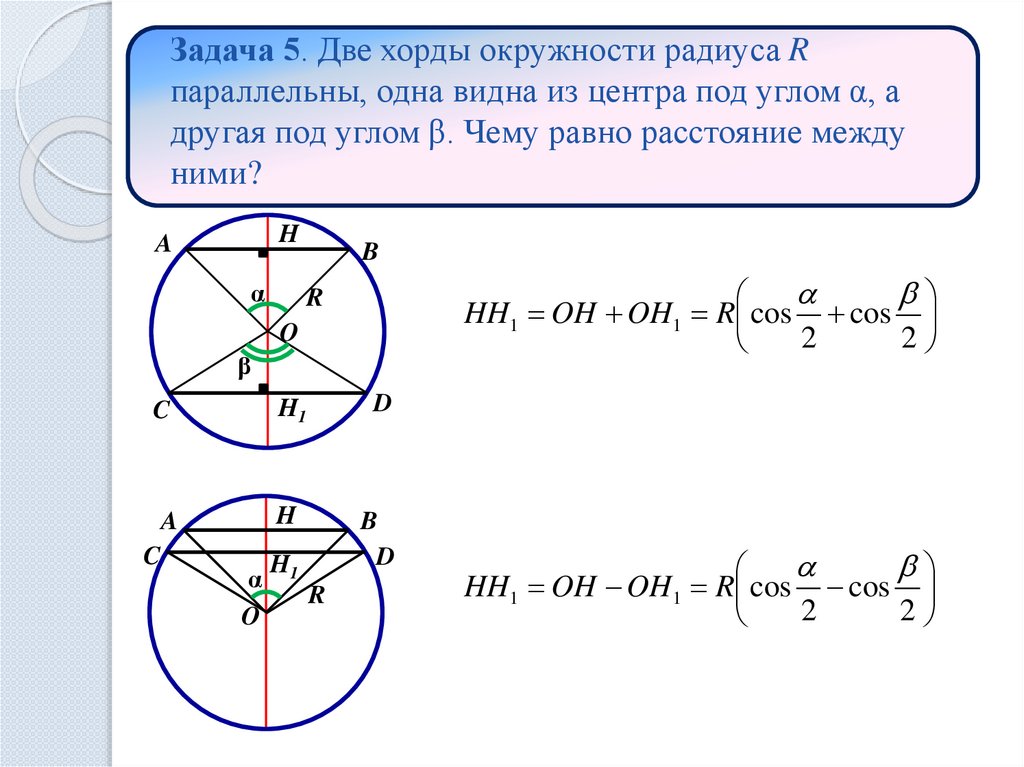
Задача 5. Две хорды окружности радиуса R
параллельны, одна видна из центра под углом α, а
другая под углом β. Чему равно расстояние между
ними?
H
A
α
B
HH1 OH OH1 R cos cos
2
2
R
O
β
C
H1
D
A
H
B
D
C
α
O
H1
R
HH1 OH OH1 R cos cos
2
2

10.

Задача 6. В круге радиусом R через точку внутри его
проведены две взаимно перпендикулярные хорды
длиной d. а) Найдите расстояние от центра круга до
точки пересечения хорд. б) Найдите расстояние между
концами этих хорд. в) Решите задачу б), если длины
хорд равны d1 и d2 . г) Решите задачу б), если длины хорд
равны d, а угол между ними φ.
Решение:
a) OH AB, OH 1 CD AH 0.5 AB 0.5d
ODH 0.5CD 0.5d OH OH1
Четырёхугольник OHEH1 – квадрат.
OE OH 2 2R 2 0.5d 2
B
E
C
H
H1
O
б) AD AE 2 ( AH OH1 ) 2
(0.5d R 2 0,25d 2 ) 2
А
CB BE 2 ( BH EH ) 2 (0.5d R 2 0,25d 2 ) 2 .
D

11.

в) AB d1 , CD d 2
AE AH OH 1 0.5d1 R 2 0.25d 22 ,
B
C
E
H
H1
O
DE DH 1 OH 0.5d 2 R 2 0.25d12 .
AD AE 2 ED 2
А
(0.5d1 R 2 0.25d 22 ) 2 (0.5d 2 R 2 0.25d12 ) 2
CB BE 2 CE 2
(0.5d1 R 2 0.25d 22 ) 2 (0.5d 2 R 2 0.25d12 ) 2
D

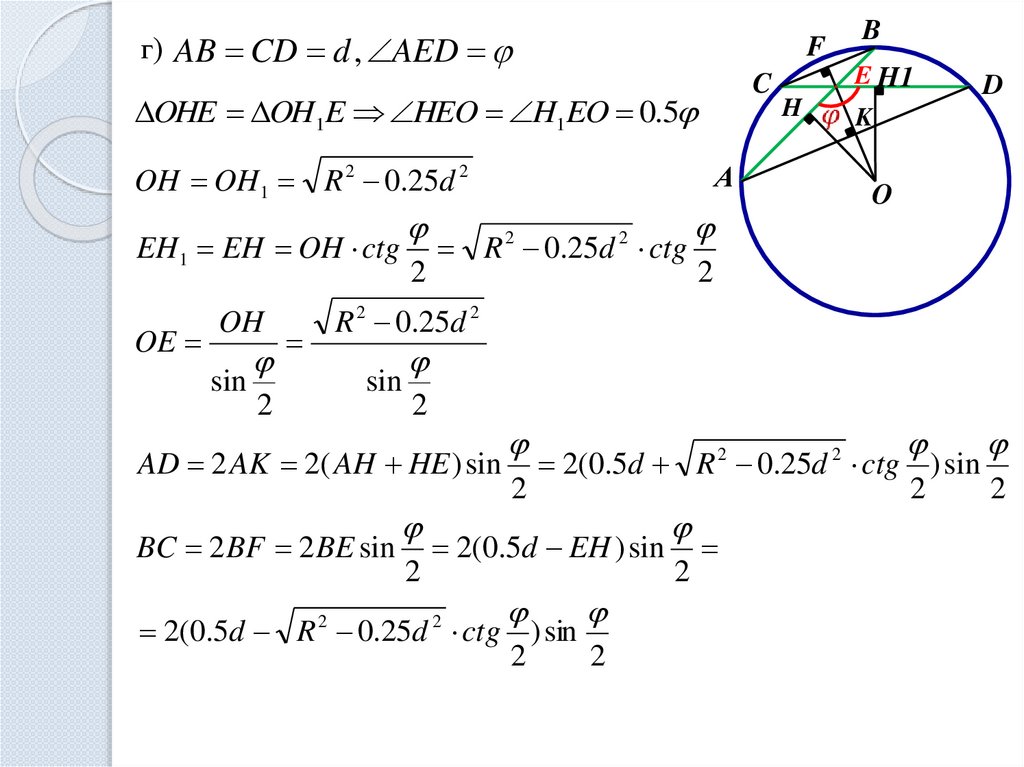
12.

г) AB CD d , AED
C
OHE OH1E HEO H1EO 0.5
OH OH1 R 2 0.25d 2
EH1 EH OH ctg
OE
OH
sin
2
2
B
F
H
. E H1
K
А
R 2 0.25d 2 ctg
D
O
2
R 2 0.25d 2
sin
2
AD 2 AK 2( AH HE ) sin
BC 2 BF 2 BE sin
2
2(0.5d R 0.25d ctg ) sin
2
2
2
2
2(0.5d EH ) sin
2(0.5d R 2 0.25d 2 ctg ) sin
2
2
2
2

13.

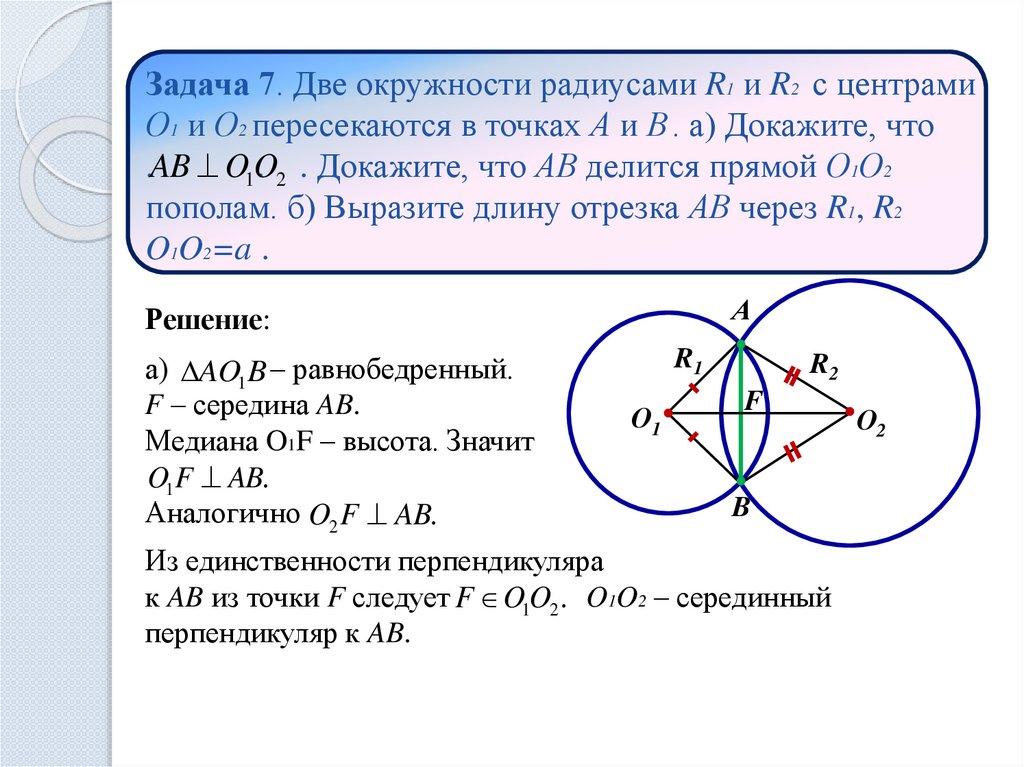
Задача 7. Две окружности радиусами R1 и R2 с центрами
О1 и О2 пересекаются в точках А и В . а) Докажите, что
.AB O1O
. 2 . Докажите, что АВ делится прямой О1О2
пополам. б) Выразите длину отрезка АВ через R1, R2
O1O2=a .
А
Решение:
а) AO1B – равнобедренный.
F – середина AB.
Медиана O1F – высота. Значит
O1F AB.
Аналогично O2 F AB.
R1
О1
R2
F
B
Из единственности перпендикуляра
к AB из точки F следует F O1O2 . O1O2 – серединный
перпендикуляр к AB.
О2

14.

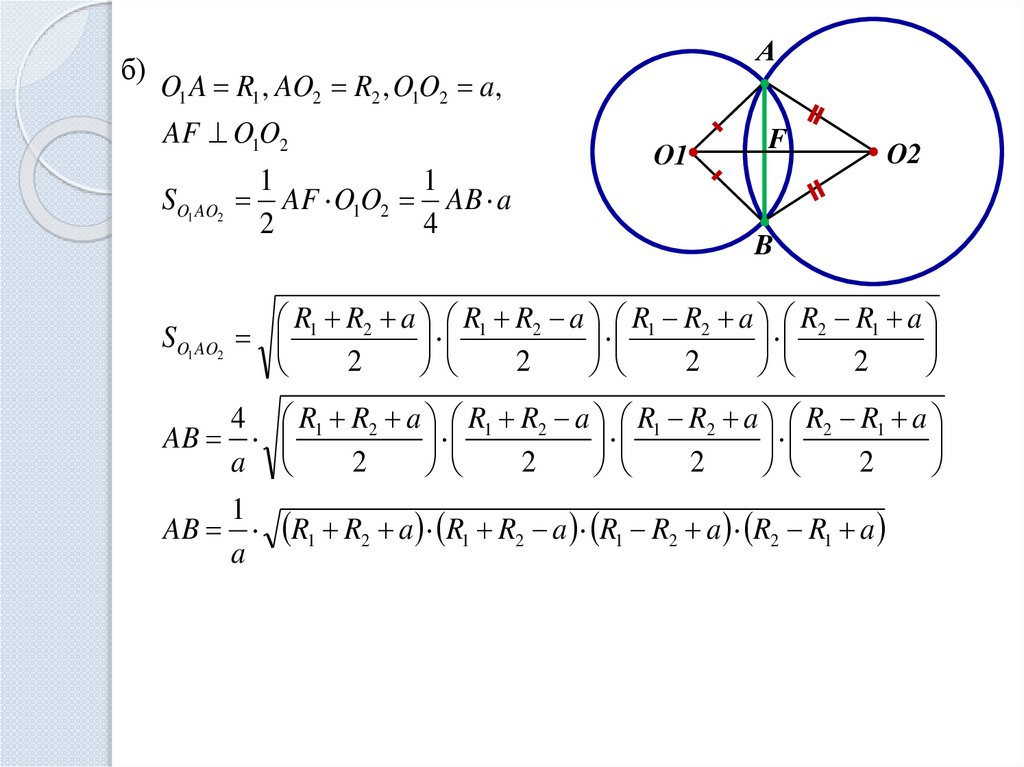
б)
А
O1 A R1 , AO2 R2 , O1O2 a,
AF O1O2
SO1 AO2
1
1
AF O1O2 AB a
2
4
О1
F
O2
B
R1 R2 a R1 R2 a R1 R2 a R2 R1 a
SO1 AO2
2
2
2
2
4 R R a R1 R2 a R1 R2 a R2 R1 a
AB 1 2
a
2
2
2
2
1
AB R1 R2 a R1 R2 a R1 R2 a R2 R1 a
a

15.

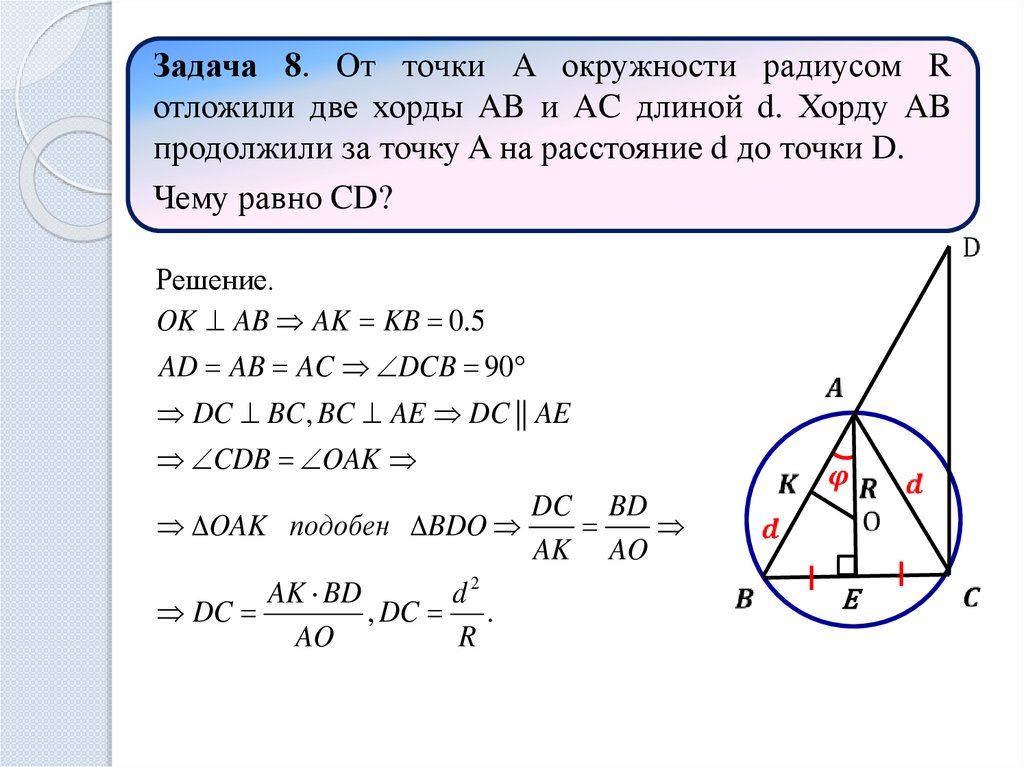
Задача 8. От точки A окружности радиусом R
отложили две хорды AB и AC длиной d. Хорду AB
продолжили за точку A на расстояние d до точки D.
Чему равно CD?
Решение.
OK AB AK KB 0.5
AD AB AC DCB 90
DC BC , BC AE DC || AE
CDB OAK
DC BD
OAK подобен BDO
AK AO
AK BD
d2
DC
, DC .
AO
R
E