Похожие презентации:
Деление «уголком» многочлена на многочлен
1.
Деление«уголком»
многочлена на
многочлен
2.
ПовторениеВыполнить деление:
1) 9х³ : 3х² = 3х
4) -х³ : 2х² =-0,5х
2) − 4х² : 4х = -х
5) − 3х² : 2х² =-1,5
3) 16х³ : 2х =8х²
6) х³ : 5х =0,2х²
Выполнить вычитание:
1). 3х³ − 5х² − 6х
─
3х³ + х² − 4х
− 6х² − 2х
2). − 4х² − х + 5
─
− 4х² − 5х
3). 6х³ + 11х² − 1
─
6х³ + 9х² − 3х
4х + 5
2х² + 3х−1
3.
Многочлены 5х² − 6х − 2; − 4х³ + 2х² − 3хзаписаны в стандартном виде , и показатели
степеней буквы х расположены в порядке
убывания.
Тогда первый член многочлена − это его
старший член;
показатель степени буквы х в старшем члене −
это
степень многочлена;
член многочлена, не содержащий буквы х − это
свободный член.
5х² − 6х − 2 − это многочлен второй
степени;
− 4х³ + 2х² − 3х − это многочлен третьей степени.
4.
Деление многочленовнацело
При сложении, вычитании, умножении многочленов
получается многочлен, например:
1. (5х²+3х+6)+(−3х²+4х−9)= 5х²+3х+6−3х²+4х−9 = 2х²+7х−3;
2. (−2х²+7х)−(3х²+х+1)= −2х²+7х−3х² − х−1= − 5х² + 6х−1;
3. (х+5)(х²−3) = х³ − 3х + 5х² − 15.
При делении многочлена на многочлен может получиться
многочлен, тогда деление выполнено нацело.
5.
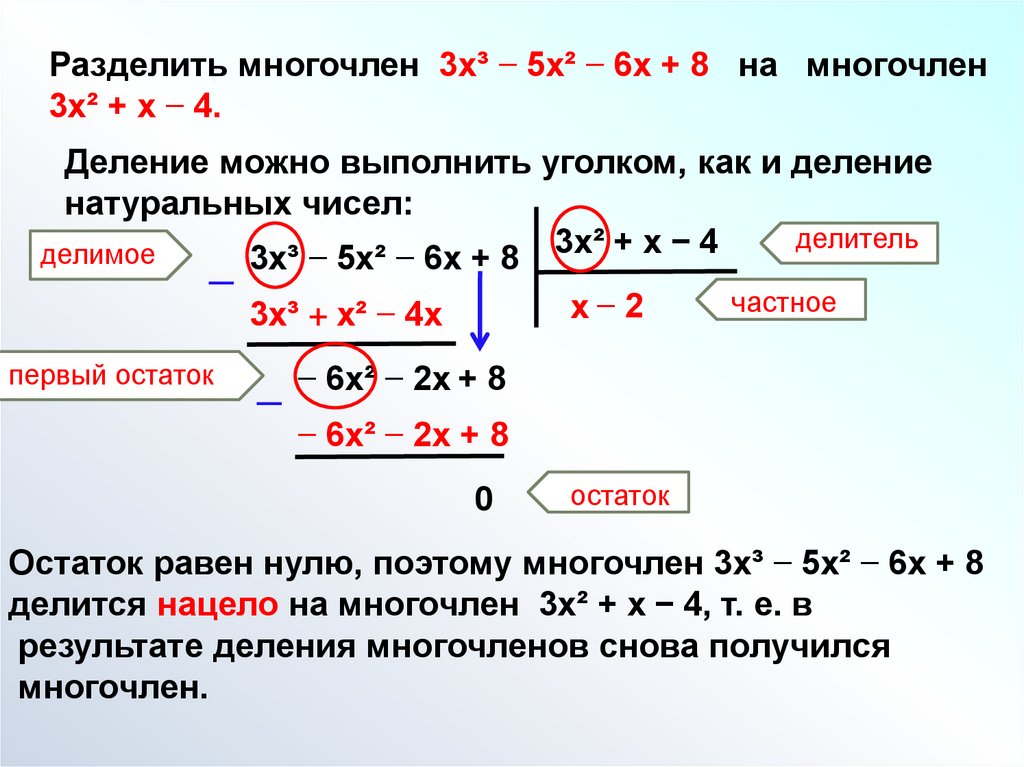
Разделить многочлен 3х³ − 5х² − 6х + 8 на многочлен3х² + х − 4.
Деление можно выполнить уголком, как и деление
натуральных чисел:
делитель
3х²
+
х
−
4
делимое
делимое
3х³ − 5х² − 6х + 8
─
частное
х− 2
3х³ + х² − 4х
делимое
делимое
─
− 6х² − 2х + 8
− 6х² − 2х + 8
0
делимое
первый
остаток
делимое
остаток
Остаток равен нулю, поэтому многочлен 3х³ − 5х² − 6х + 8
делится нацело на многочлен 3х² + х − 4, т. е. в
результате деления многочленов снова получился
многочлен.
6.
Алгоритм деления многочленов уголком1. Расположить делимое и делитель по убывающим
степеням переменной х.
2. Разделить старший член делимого на старший член
делителя;
полученный одночлен записать первым членом частного.
3. Первый член частного умножить на делитель,
результат вычесть из делимого;
полученная разность является первым остатком.
4. Старший член этого остатка разделить на старший
член делителя; полученный одночлен записать вторым
членом частного и умножить его на делитель;
результат вычесть из первого остатка; получим
второй остаток и т. д.
Это следует продолжить до тех пор, пока не будет
получен остаток, равный нулю.
7. Деление многочлена «уголком»
8.
Найти частное (результат проверить умножением):1) (х² − 2х − 35) : (х − 7);
х² − 2х − 35
─
х² − 7х
5х − 35
─
5х − 35
0
х − 7
х +5
2) (− 4х² − х + 5) : (4х + 5);
− 4х² − х + 5 4х + 5
─
−х+1
− 4х² − 5х
─ 4х + 5
4х + 5
0
(х + 5) (х − 7) = х² − 7х + 5х − 35 = х² − 2х − 35;
(4х + 5) ( − х + 1) = − 4х² − 5х + 4х + 5 = − 4х² − х + 5.
9.
Деление многочленов с остаткомРазделить многочлен х³ − х² − 2х + 4 на многочлен
х² − 3х + 1.
Выполним деление уголком:
х² − 3х + 1
х³ − х² − 2х + 4
─
х +2
х³ − 3х² + х
2х² − 3х+ 4
─
2х² − 6х + 2
3х + 2
Дальнейшее деление
невозможно, так как степень
последнего остатка 1
меньше степени делителя 2.
Ответ: частное х + 2, остаток 3х + 2.










 Математика
Математика








