Похожие презентации:
Квадратные неравенства (Метод интервалов)
1.
Квадратныенеравенства
(Метод
интервалов)
2.
Алгоритм решения квадратных неравенствметодом интервалов
1. Найти нули функции.
2. Отметить их на координатном луче.
3. Показать интервалы.
4. Найти знак функции в каждом промежутке
5. Выбрать промежуток, соответствующий
знаку неравенства:
«+» – знак «>»
« – » – знак «<»
3.
Решить неравенство -4х2 + 27х +7 0.Решение.
-4х2 + 27х +7 0,
4х2 - 27х -7 0.
1) Рассмотрим f(x) = 4х2 - 27х -7 и найдем значения х, при
которых f(x) 0, D(f) = R.
2) 4х2 - 27х -7 = 0, D = 272 - 4*4*(-7) = 729 + 112 = 841 = 292.
х1 = (27 – 29) : 8 = -0,25;
х2 = (27 + 29) : 8 = 7.
3) 4х2 - 27х -7 = 4(х + 0,25)(х – 7).
4)
5) f(x) 0 при –0,25 х 7.
Ответ: [-0,25; 7].
4.
Знак дроби совпадает со знаком произведения.Поэтому данное неравенство равносильно неравенству
Нули функции: х=7; х=-2
-
+
-2
Ответ:
7
5.
-+
+
6.
Определение модуляМодулем действительного числа а называется
само это число, если оно неотрицательное, и
противоположное ему число, если данное число
отрицательно.
Из определения модуля следует:
7.
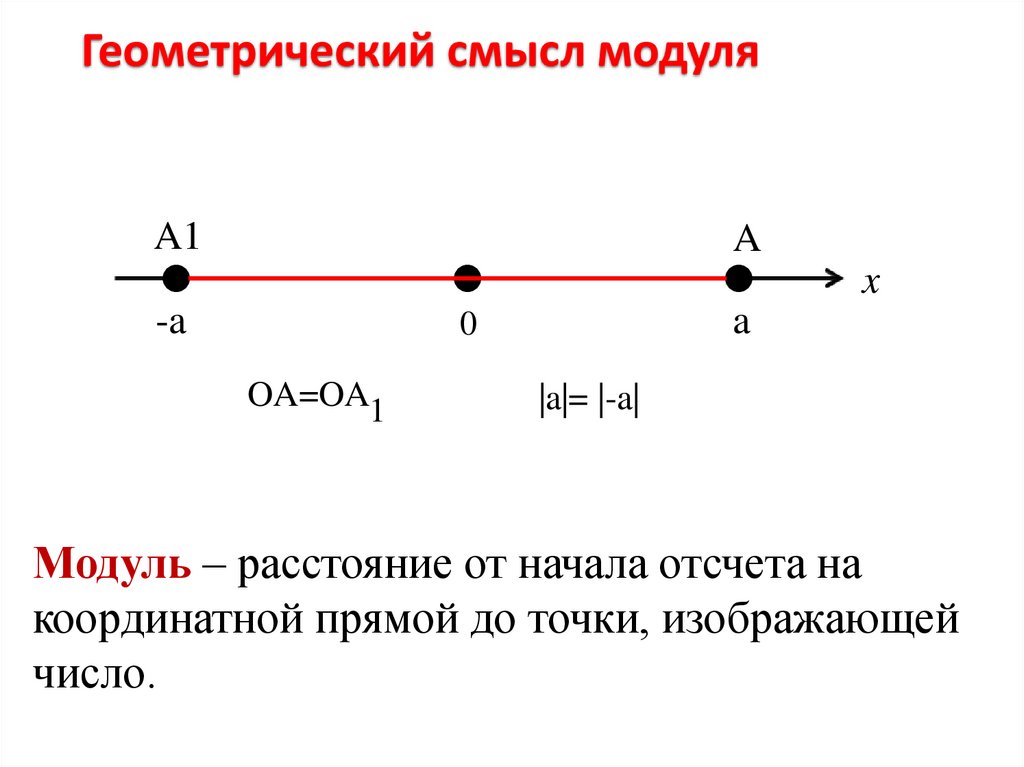
Геометрический смысл модуляA1
A
x
-a
a
0
OA=OA1
|a|= |-a|
Модуль – расстояние от начала отсчета на
координатной прямой до точки, изображающей
число.
8.
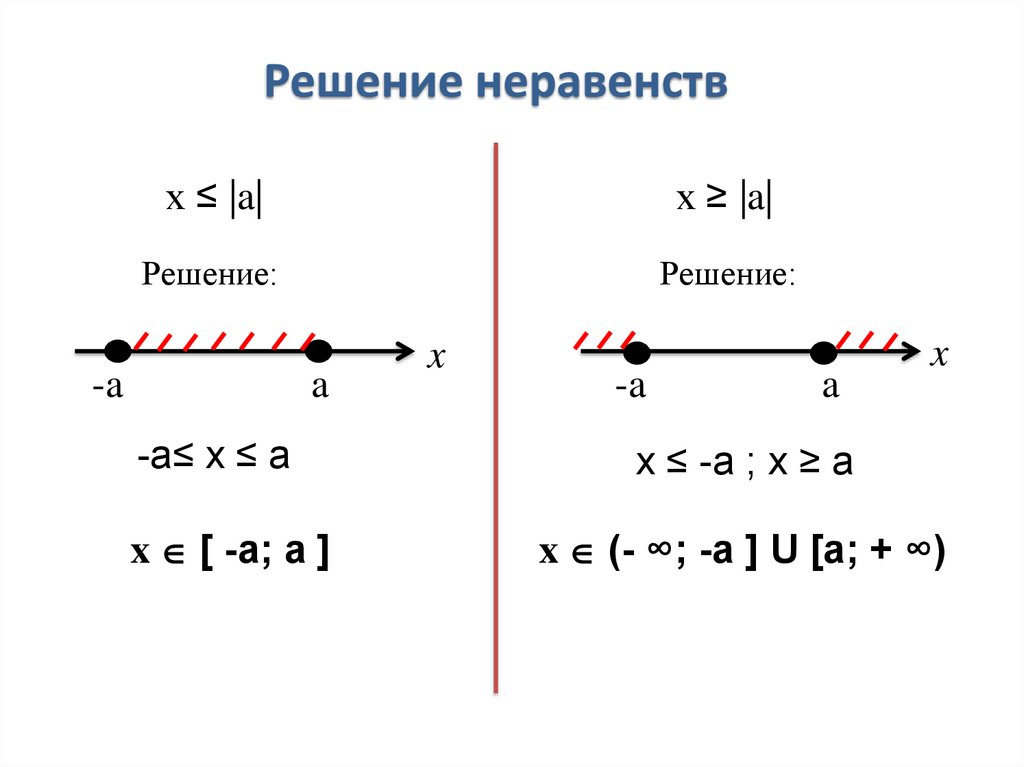
Решение неравенствх ≤ |a|
х ≥ |a|
Решение:
Решение:
-a
a
x
-a
a
x
-a≤ х ≤ a
х ≤ -a ; x ≥ a
x [ -a; a ]
x (- ∞; -a ] U [a; + ∞)
9.
Геометрическое истолкование выраженияЭто расстояние от координатной (числовой) прямой между
точками x и a, которое обозначается
Примеры:




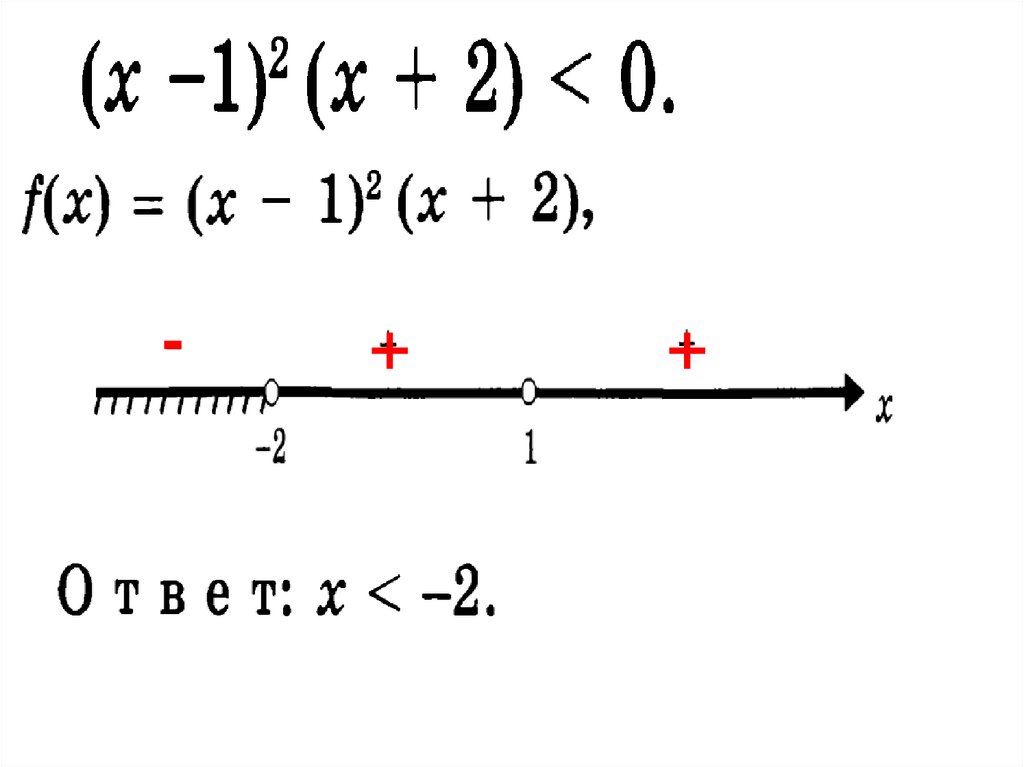


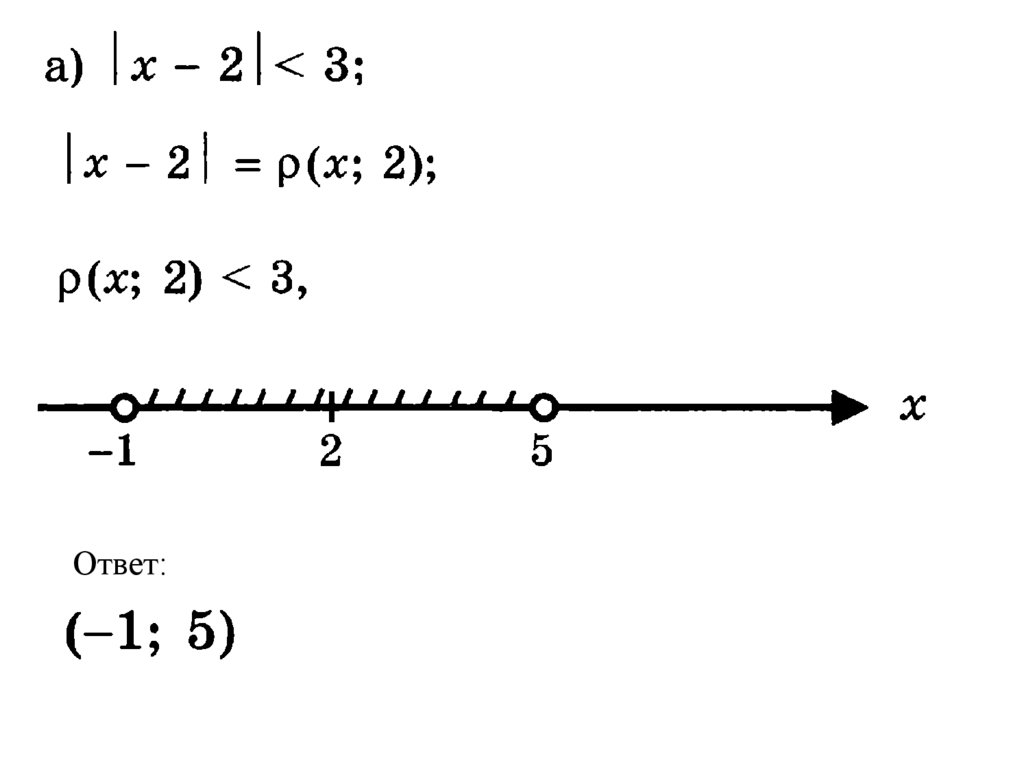
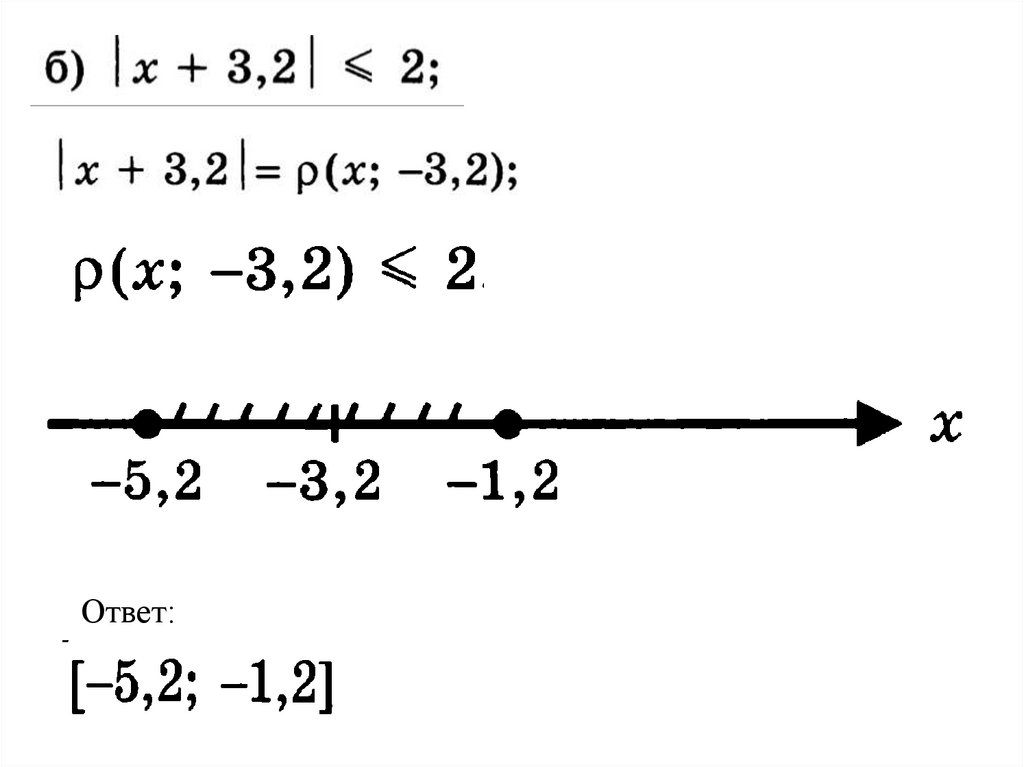
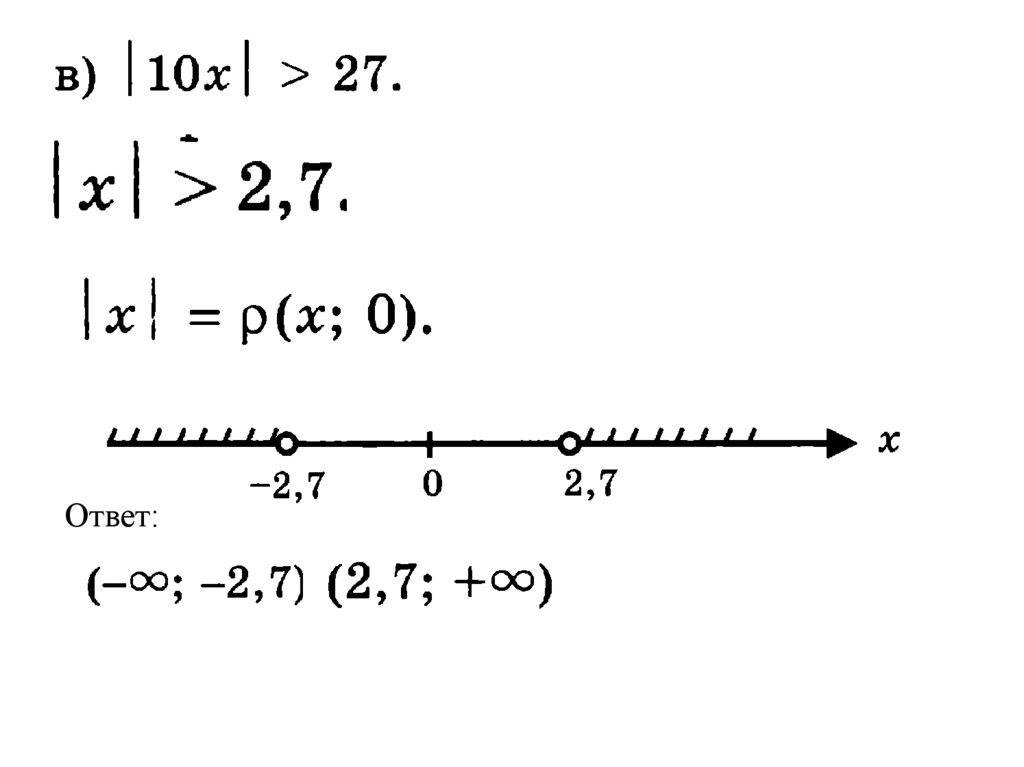
 Математика
Математика








