Метод неопределенных коэффициентов

1. Метод неопределенных коэффициентов

2.

3.

Цели урока
Ты узнаешь:
метод неопределенных коэффициентов.
Ты научишься:
раскладывать многочлен на множители с помощью
метода неопределенных коэффициентов.

4.

Алгоритм деления многочленов уголком
1. Расположить делимое и делитель по убывающим
степеням переменной х.
2. Разделить старший член делимого на старший член
делителя;
полученный одночлен записать первым членом частного.
3. Первый член частного умножить на делитель,
результат вычесть из делимого;
полученная разность является первым остатком.
4. Старший член этого остатка разделить на старший
член делителя; полученный одночлен записать вторым
членом частного и умножить его на делитель;
результат вычесть из первого остатка; получим
второй остаток и т. д.
Это следует продолжить до тех пор, пока не будет
получен остаток, равный нулю.

5. Деление многочлена «уголком»

6.

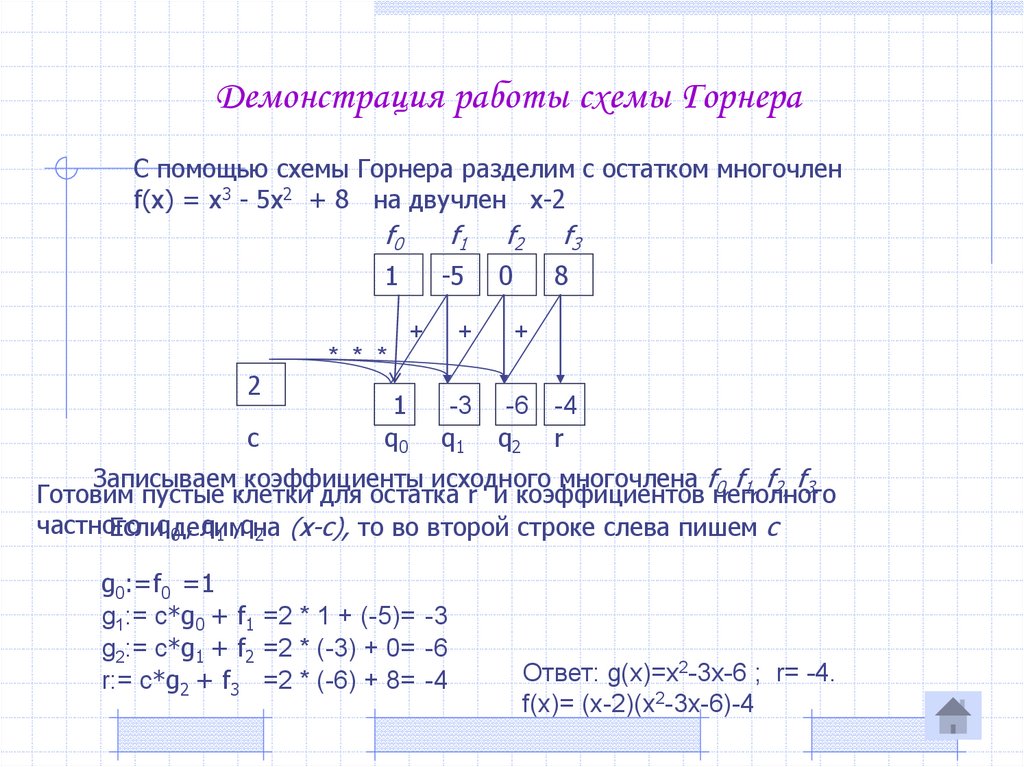
Демонстрация работы схемы Горнера
С помощью схемы Горнера разделим с остатком многочлен
f(x) = x3 - 5x2 + 8 на двучлен x-2
f0
f1
f2
f3
1
-5
0
8
+
2
c
+
+
-3
q1
-6 -4
q2 r
* * *
1
q0
Записываем коэффициенты исходного многочлена f0, f1, f2, f3.
Готовим пустые клетки для остатка r и коэффициентов неполного
частного
, q1 ,qна
Еслиq0делим
2 (x-c), то во второй строке слева пишем с
g0:=f0 =1
g1:= с*g0 + f1 =2 * 1 + (-5)= -3
g2:= с*g1 + f2 =2 * (-3) + 0= -6
r:= с*g2 + f3 =2 * (-6) + 8= -4
Ответ: g(x)=x2-3x-6 ; r= -4.
f(x)= (x-2)(x2-3x-6)-4

7.

Метод неопределённых коэффициентов –
это метод, применяемый в математике
для нахождения коэффициентов
выражений, вид которых заранее
известен.

8.

Теорема 1 (о многочлене, тождественно равном нулю).
Если при произвольных значениях аргумента х значение многочлена