Похожие презентации:
Виды неопределенностей и методы их разрешения
1.
Виды неопределенностей и методы их разрешения.Существует несколько видов неопределенностей
0
0
0
,
,
0
,
1
,
,
,
0
.
0
Неопределенность вида
(бесконечность деленная
на бесконечность).
Выражение под знаком предела представляет собой
частное многочленов любой степени.
Pn ( x)
f ( x)
Qm ( x)
2.
Дляраскрытия
такого
вида
неопределенности
необходимо:
1. разделить все слагаемые числителя и знаменателя на
переменную х в старшей степени;
2. рассмотреть предел каждого слагаемого.
При раскрытии неопределенности такого вида возможны
три случая:
а). Степень многочлена числителя равна степени
многочлена знаменателя.
10 8
3x 2 10 x 8
3 2
2 2
2
2
3x 10 x 8 lim x
x x 3
x
x lim
lim 2
. x 2
x
5 4
x 5x 4
x x 5 x 4
1
2
x
x
x2 x2 x2
3.
На основании теоремы о пределе частного, суммы(разности) рассмотрим предел каждого слагаемого
10
lim
0;
x x
8
lim 2 0;
x x
5
lim 0;
x x
4
lim 2 0.
x x
3 1
2 2 3
2 x3 3x 1
2 0 0 2
x
x
lim 3
lim
;
2
x 3 x x 5
3 0 0 3
x 3 1 5
x x3
5 1
7 2 4
7 x4 5x2 1
7 0 0 7
x
x
lim 4
lim
;
3
x 6 x 5 x 8
6 0 0 6
x 6 5 8
x x4
4.
б).Степень многочлена числителя больше степени
многочлена знаменателя
5 7
3x 2 5 x 7
3
2
2
2
2
2
3x 5 x 7
3
x
x
x
x
x
lim
lim
lim
x
2 1
x
2x 1
0
x
2x 1
2
2
x x2
x
x
x5 6 x3 11x 2 5
5 5 5
5
3
2
5
x 6 x 11x 5 lim x
x
x
x
lim
x
4
2
4
2
3
x
x
8x
x
3x x 8 x
5 5
5
x
x
x
lim
x
6 11 5
3 5
2
x
x
x 1
0
3 1 8
3 4
x x
x
1
5.
в). степеньмногочлена числителя меньше степени
многочлена знаменателя
2 x 4 4 x3 x 2
6 6
6
2 x 4 4 x3 x 2
lim
x
x
x
lim 6
6
5
4
5
4
x
4 x 5 x 3x
x
4
x 4 x 5 x 3x x 4
x6
x6
x6 x6 x6
2 4 1
3 4
2
0
x
x
x
lim
0
x
5 3 1 4 4
4 2 5 6
x
x
x
x
6.
Предел отношения двух многочленов при хравен
0 при n m
Pn ( x) a1
lim
при n m
x Q ( x )
m
a2
при n m
1. если степень многочлена числителя меньше степени
многочлена знаменателя, по предел равен нулю.
2. если степень многочлена числителя равна степени
многочлена знаменателя, то предел равен отношению
коэффициентов при старшей степени переменной;
3. если степень многочлена числителя больше степени
многочлена знаменателя, по предел равен бесконечности;
7.
2. Неопределенность вида0 .
0
Метод раскрытия неопределенности такого вида зависит
от выражения стоящего под знаком предела, как правило
выделяют два частных случая:
а). выражение стоящее под знаком предела является
рациональной функцией:
2
x 4 0
lim 3
x 2 x 8
0
Для решения задачи необходимо
формулами сокращенного умножения:
воспользоваться
a2 b2 a b a b a3 b3 a b a 2 ab b 2 .
8.
Разложим числитель и знаменатель на множители:x 2 x 2
x2 4 0
lim 3
lim
2
x
2
x 2 x 8
x 2 x 2x 4
0
x 2
2 2
1
lim 2
2
.
x 2 x 2 x 4
2 2 2 4 3
Если числитель и знаменатель дробно-рациональной
функции являются многочленами второй степени, то для
раскрытия неопределенности необходимо разложить и
числитель и знаменатель на множители:
2
x2 4 x 5 0
ax
bx c a x x1 x x2
lim 2
;
x 1 x 2 x 3
0
9.
Для решения задачи необходимо1. Определить корни числителя и знаменателя
x2 4 x 5 0
b D
x1,2
2a
x2 5
x1 1
x2 2 x 3 0
x1 1
D b2 4ac
x2 3
2. Разложить многочлен на множители
x 4 x 5 ( x 1)( x 5)
2
x 2 2 x 3 ( x 1)( x 3)
x 1 x 5
x2 4x 5 0
x 5 3
lim 2
lim
lim
.
x 1 x 2 x 3
0 x 1 x 1 x 3 x 1 x 3 2
10.
Рассмотрим пример:3 x 2 10 x 8 0
lim
x 4 x 2 5 x 4
0
Вычислим корни многочлена числителя и знаменателя,
разложим числитель и знаменатель на множители:
3x 2 10 x 8 0;
2
x1 4; x 2 .
3
x2 5x 4 0;
x1 4; x2 1.
2
2
3(
x
4)(
x
)
3(
x
)
3 x 2 10 x 8
3 lim
3
lim
lim 2
x 4 ( x 4)( x 1)
x 4 ( x 1)
x 4 x 5 x 4
3 x 2 3( 4) 2 14
x 4 ( x 1)
4 1
3
lim
11.
б). выражение стоящее под знаком предела, содержитдробно-иррациональную функцию
В этом случае для раскрытия неопределенности
умножают и числитель и знаменатель на выражение
сопряженное к иррациональному выражению и используют
формулу сокращенного умножения
a b a b a 2 b 2 .
Например, знаменатель дроби является иррациональным
выражением
( x 3)( x 2 8 x )
x 3
0 lim
lim
x 3
x 3
( x 2 8 x )( x 2 8 x )
x 2 8 x 0
12.
( x 3)( x 2 8 x )( x 3)( x 2 8 x )
lim
lim
x 3
x 3
x 2 8 x
( x 2) (8 x)
( x 3)( x 2 8 x )
( x 3)( x 2 8 x )
lim
lim
x
3
x 3
2( x 3)
2x 6
x 2 8 x
3 2 8 3
lim
5
x 3
2
2
13.
Рассмотрим пример, когда числитель дроби являетсяиррациональным выражением
2 x 2 x
2 x 2 x
2 x 2 x 0
lim
lim
x
0
x 0
x
x 2 x 2 x
0
lim
x 0
x
lim
x 0
x
2 x 2 x
Пример:
2 x 2 x
lim
x 0
2x
2 x 2 x
x
lim
x 0
2 x 2 x
2 x 2 x
2
2
1
2 x 2 x 2 2
2
2 x
0
lim
x 4 3 2 x 1
0
14.
В этом случае и числитель и знаменатель содержатиррациональные выражения.
2 x
(2 x )(2 x )(3 2 x 1)
0
lim
lim
x 4 3 2 x 1
x
4
(3 2 x 1)(3 2 x 1)(2 x )
0
(4 x)(3 2 x 1)
(4 x)(3 2 x 1)
lim
lim
x 4 (9 (2 x 1))(2
x
4
x)
(9 2 x 1)(2 x )
(4 x)(3 2 x 1)
(4 x)(3 2 x 1)
lim
lim
x 4 (8 2 x )(2
x 4 2(4 x )(2
x)
x)
3 2 4 1 3
4
2(2 4)
15.
Первый замечательный пределsin x 0
lim
1
x 0
x
0
lim
x 0
sin x
x
1,
1. lim
x 0 sin x
x
Если выражение, стоящее под знаком предела содержит
тригонометрические
функции,
то
для
раскрытия
неопределенности
используют
формулу
первого
замечательного предела.
Формулы, используемые при решении
x
1 cos x 2sin
2
2
sin х cos х 1
2
2sin х cos х sin 2 х
2
16.
Рассмотрим примерsin 2 x 0 lim 2sin 2 x 2lim sin 2 x 2 1 2
lim
x 0
x 0 7 2 x
7 7
7 2x
x 0
7x
0
1 cos5 x
x 0 1 cos3 x
lim
5x
2sin
2
lim
x 0
3x
2sin 2
2
2
5x
sin
2
lim
x 0
3x
sin 2
2
2
2
5x
5 x 3x 3x 5 x 5 x
25
x
sin sin
25
2
2
2
2
2
2
4
lim
lim
2
x 0 5 x
9
5x
3x
3 x 3 x 3 x x 0 9 x
sin
sin
4
2
2
2
2 2 2
17.
cos 7 xlimsin 3 x ctg 7 x 0 limsin 3 x
lim sin 3 x
x 0
x 0
sin 7 x x 0 sin 7 x
sin 3x 3x 7 x
lim
x 0 3 x
sin 7 x 7 x
3x 3
lim
x 0 7 x
7
lim tg 5 x ctg 6 x 0 lim
x 0
x 0
sin 5 x cos 6 x
cos5 x sin 6 x
sin 5 x 5 x 6 x
5х 5
lim
lim
x 0 5 x
sin 6 x 6 x x 0 6 х 6
arctg 4 x 0
arctg 4 x 4
4 А
lim
lim
lim
2
x 0
x 0 x
x
0 x 0 4 x x
0
18.
21 cos12 x 0
2sin
6x
2
lim
1 cos12 x 2sin 6 x lim
x 0
x 0 x sin x
x sin x
0
2sin 6 x sin 6 x 6 x 6 x lim 72 x 72
lim
x 0
x
x 0
6 x 6 x x sin x
2sin 3 x cos3 x
2sin 3x 3x 5 x
1 cos 6 x 0
lim
lim 2
lim
2
2
x
0
x 0
x 0 x sin 5 x
x sin 5 x
3x sin 5 x 5 x x
0
2 3x
6
lim
2
2
x 0 5 x x
x 0 5 x
lim
19.
3. Неопределенность вида1
Для
раскрытия
неопределенностей
применяется второй замечательный предел:
lim 1
x
x
такого
1
x
1
e,
x
lim(1 x) e
x 0
Рассмотрим пример:
2x 3
lim
x 3 x 4
2x 3
lim
x 3 x 4
x 1
x 1
2x
lim
x 3 x
2x
xlim
3 x
x 1
x 1
2
3
2
3
0
вида
20.
Пример:3x 5
lim
x 3 x 7
2 x 1
12
3x 7
lim
x
3x 7 3x 7
3x 7 7 5
lim
x
3x 7
2 x 1
1
lim 1
x
3x 7
12
2 x 1
2 x 1
21.
1lim 1
x
3x 7
12
3 x 7 12
(2 x 1)
12 3 x 7
lim e
x
12(2 x 1)
3 x 7
е
lim
x
24 x 12
3 x 7
e8
24 x 12 24
так как lim
8
3
x 3 x 7
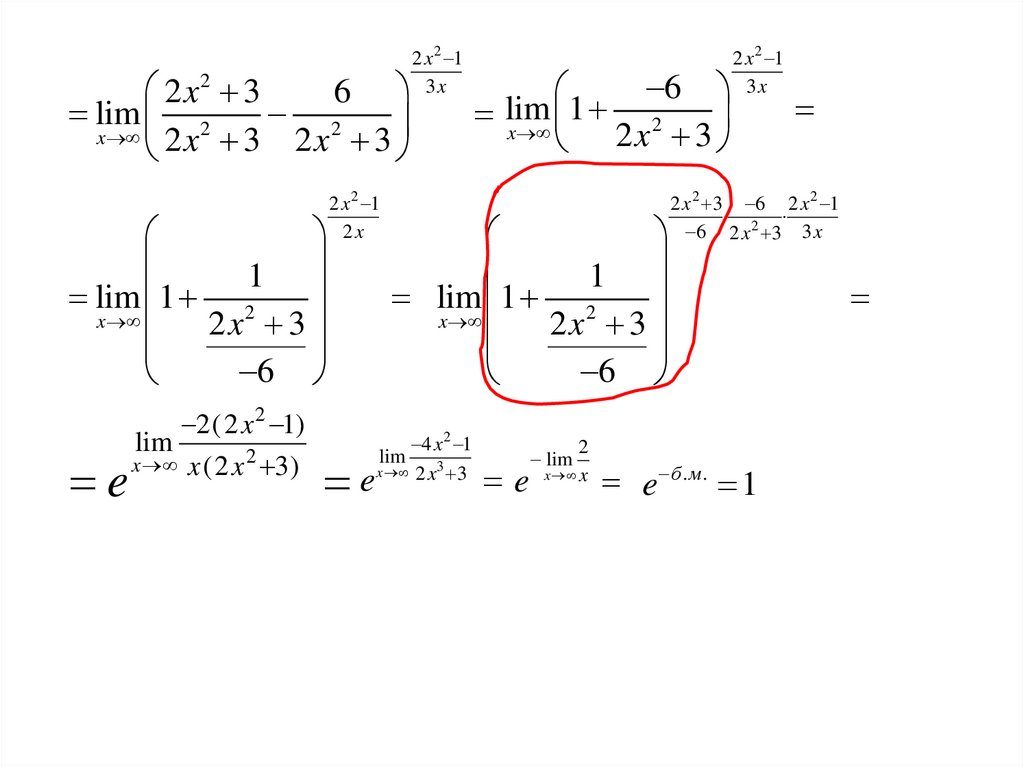
Пример:
2 x2 3
lim 2
x 2 x 3
2 x 2 1
3x
2 x2 3 3 3
lim
2
x
2x 3
2 x 2 1
3x
22.
2 x2 36
lim 2
2
x 2 x 3
2
x
3
1
lim 1 2
x
2x 3
6
e
2(2 x 2 1)
lim
x x (2 x 2 3)
2 x 2 1
2x
e
2 x 2 1
3x
6
lim
1 2
x
2
x
3
1
lim 1 2
x
2 x 3
6
4 x 2 1
lim
x 2 x3 3
e
2
x x
lim
2 x 2 1
3x
2 x 2 3 6 2 x 2 1
6 2 x 2 3 3 x
e б . м. 1
23.
Пример3x 2 5
lim 2
x 3 x 7
5 x 4 2
2x
2
3
x
7 7 5
1 lim
2
x
3
x
7
1
lim 1 2
x
3
x
7
12
5 x4 2
2x
3 x 2 7 12 5 x 4 2
12 3 x 2 7 2 x
lim e 10 x e
x
10 x
lim
e
e
0
x
lim e
x
60 x 4 24
6 x3 14 x
24.
Пример:5x 7
lim
x 5 x 4
6 x 2 1
5x 4 4 7
1 lim
x
5x 4
3
5x 4
lim
x 5 x 4
5x 4
6 x 2 1
6 x 2 1
5 x 4
3
3
lim 1
x
5x 4
3
(6 x 2 1)
5 x 4
e
3(6 x 2 1)
lim
x
5 x 4
18 x
lim
2
x 5
18 x 3 e
e 0
lim
e x 5 x 4
18 x
lim
x 5
e
e
25.
Пример:lim(2 x)
2x
1 x
x 1
1 lim(1 1 x)
x 1
lim (1 (1 x))
x 1
1
1 x
1 x 2 x
1 1 x
2x
1 x
(1 x))
lim(1
x 1
e
lim 2 x
x 1
e
2
Пример:
lim(7 2 x)
x 3
2
x 3
1 lim(1 6 2 x)
x 3
2
x 3
2x
1 x
26.
lim(1 (6 2 x))2
x 3
x 3
1
6 2 x
lim (1 (6 2 x)
x 3
e
2(3 x ) 2
lim
x 3
1
x 3
e
6 2 x 2
1 x 3
4( x 3)
lim
x 3
x 3
e
4
27.
Пример:lim(2 x 3) ln( x 2) ln x
x
Для решения задач данного типа, необходимо
преобразовать выражение стоящее под знаком предела,
используя свойства логарифмической функции.
a
ln a ln b ln
Решение.
b
ln a k ln a
k
x 2
x 3) ln
lim(2 x 3) ln( x 2) ln x lim(2
x
x
x
28.
2 x 3x 2
x 2
ln lim
lim ln
x
x
x
x
2
ln lim 1
x
x
ln e
4 x 6
x x
lim
2 x 3
1
x
2
1
ln lim 1
x
x
2
ln e 4
4
2 x 3
2
(2 x 3)
x
29.
4. Неопределенность видаlim( 9 x 4 x 3 x)
2
x
Замечание: данный вид неопределенности возможен
только при x
Выражение, стоящее под знаком предела представляет
собой разность бесконечно больших величин , для раскрытия
неопределенности такого вида, необходимо умножить и
разделить исходное выражение на сопряженное выражение и
привести к виду
30.
Решение.lim( 9 x 2 4 x 3 x)
x
lim
( 9 x 2 4 x 3x)( 9 x 2 4 x 3x)
( 9 x 2 4 x 3 x)
x
lim
lim
2
x
2
x
9 x 4 x 3x
9 x 4 x 3x
9x2 4x 9x2
4x
4x
4x
4 2
lim
lim
x
9 x 2 3x x 3 x 3 x 6 3
31.
Задача о непрерывном начислении процентовПервоначальный вклад в банк составил Q0 денежных
единиц.
Банк выплачивает ежегодно р% годовых.
Определить размер вклада Qt через t лет.
Решение.
1. Простые проценты – размер вклада ежегодно
p
увеличивается на одну и туже величину
Q0
100
За год Q Q 1 p
1
0
100
2p
За два года
Q2 Q0 1
100
pt
Q
Q
1
За t лет
t
0
100
32.
2. Сложные проценты – размер вклада ежегодноувеличивается в одно и то же число раз равное
p
1
100
Таким образом
p
Q1 Q0 1
100
p
Q2 Q0 1
100
2
p
Qt Q0 1
100
t
При начислении процентов n раз в году и ежегодном
приросте р% процент начисления за 1 - часть года составит
n
p
%
n
33.
Размер вклада за t лет при nt начислениях составитьnt
p
Q lim Q0 1
n
100
n
Рассмотрим начисление процентов каждое полугодие ( n=2),
квартал (n=4), ежемесячно (n=12), непрерывно ( n ).
Размер вклада за t лет составит
pt
100 n 100
p
nt
pt
1
p
lim Q0 1
Qt lim Q0 1
Q0 e100
n
100n n 100n
p
=е
34.
Полученнаяформула
выражает
показательный
(экспоненциальный) закон роста вклада (при р>0).
Замечание. В практических финансово-кредитных
операциях непрерывно начисление применяется редко.
Этот метод применяется при анализе сложных
финансовых вопросов, таких как обоснование и выбор
инвестиционных решений.



















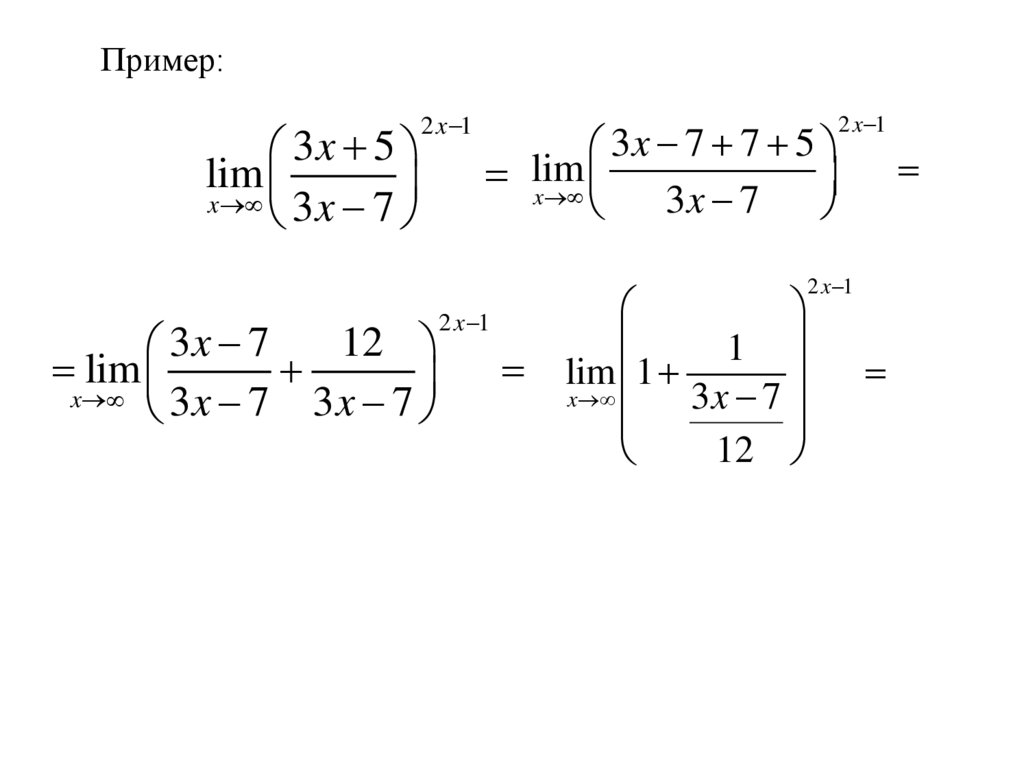



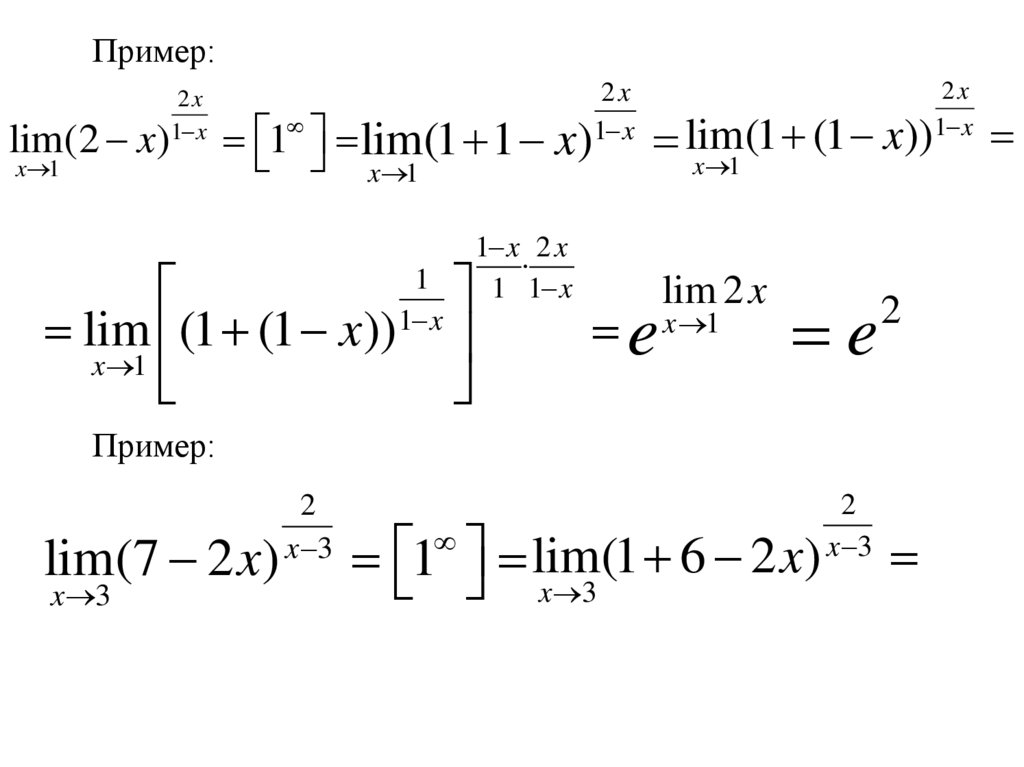









 Математика
Математика








