Векторы в пространстве. Действия над векторами. Разложение векторов

1. Векторы в пространстве. Действия над векторами. Разложение векторов.

2.

03.02.25
Раздел 5. Векторы и координаты
Тема. Векторы в пространстве. Действия над векторами.
Разложение векторов.
Вид занятия: лекционное занятие.
Преподаватель
Бондарь (Кузнецова) София Викторовна.
Специальность
«Юриспруденция».
Группы ПР-89, ПР-90, ПР-91 (очная форма обучения, 1 курс).
Время выполнения:2 часа

3. Цели

• Знать: определение вектора в
пространстве и связанные с ним
понятия; равенство векторов.
• Уметь: находить равные,
сонаправленные, противоположно
направленные векторы; решать
задачи по данной теме.

4.

Уважаемые студенты! Изучите
теоретический материал презентации,
составьте краткий конспект, ответьте на
предложенные вопросы,
проанализируйте решение задач,
запишите в тетрадь.
Фотоотчет о работе отправьте на почту
преподавателя sofiyabondar123@mail.ru

5. Понятие вектора появилось в 19 веке в работах математиков Г. Грассмана У. Гамильтона

6. Современная символика для обозначения вектора r была введена в 1853 году французским математиком О. Коши.

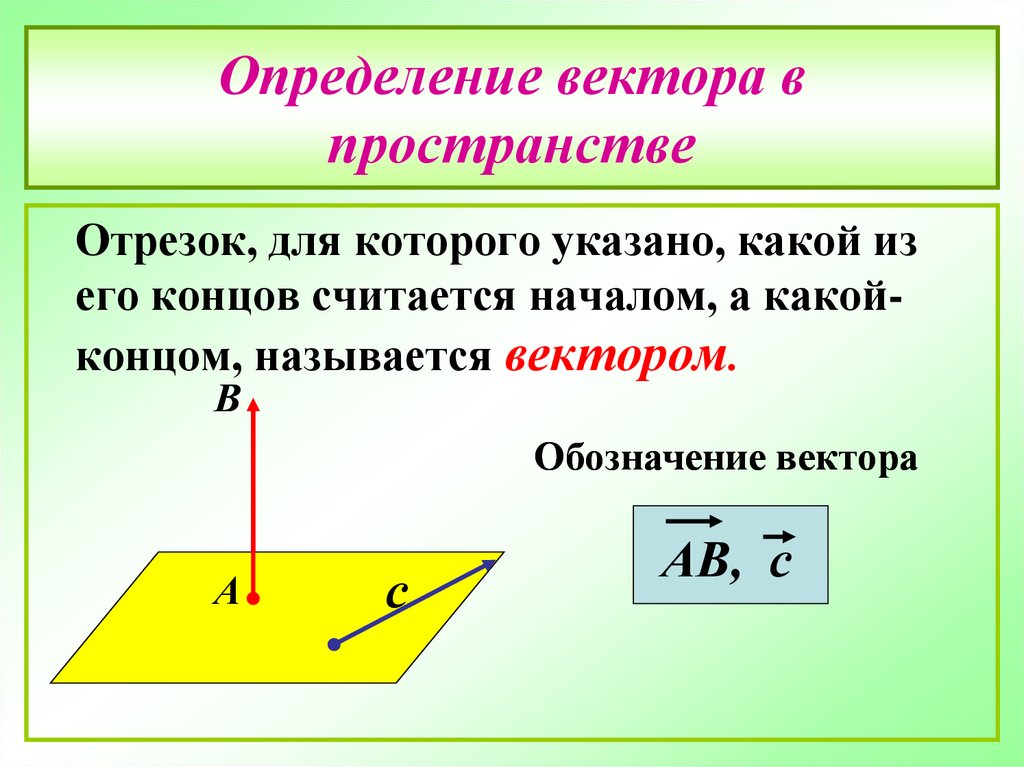
7. Определение вектора в пространстве

Отрезок, для которого указано, какой из
его концов считается началом, а какойконцом, называется вектором.
В
Обозначение вектора
А
с
АВ, с

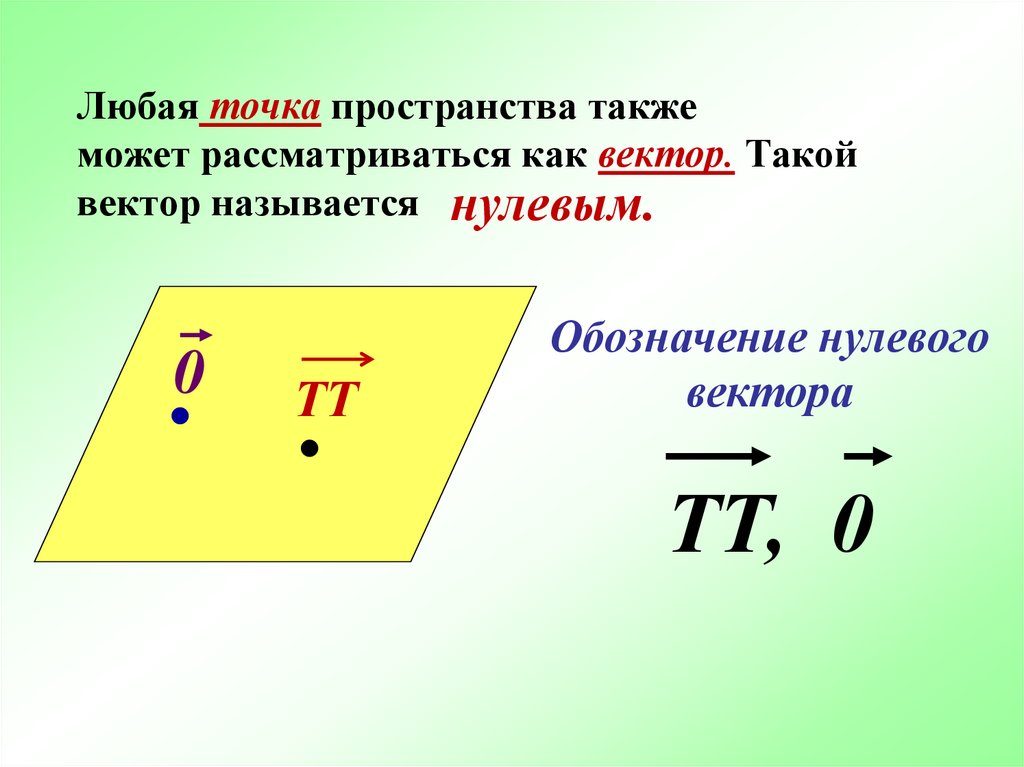
8. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется

нулевым.
0
ТТ
Обозначение нулевого
вектора
ТТ, 0

9. Длина ненулевого вектора

• Длиной вектора АВ называется длина
отрезка АВ.
• Длина вектора АВ (вектора а)
обозначается так:
АВ , а
• Длина нулевого вектора считается равной
нулю:
0 =0

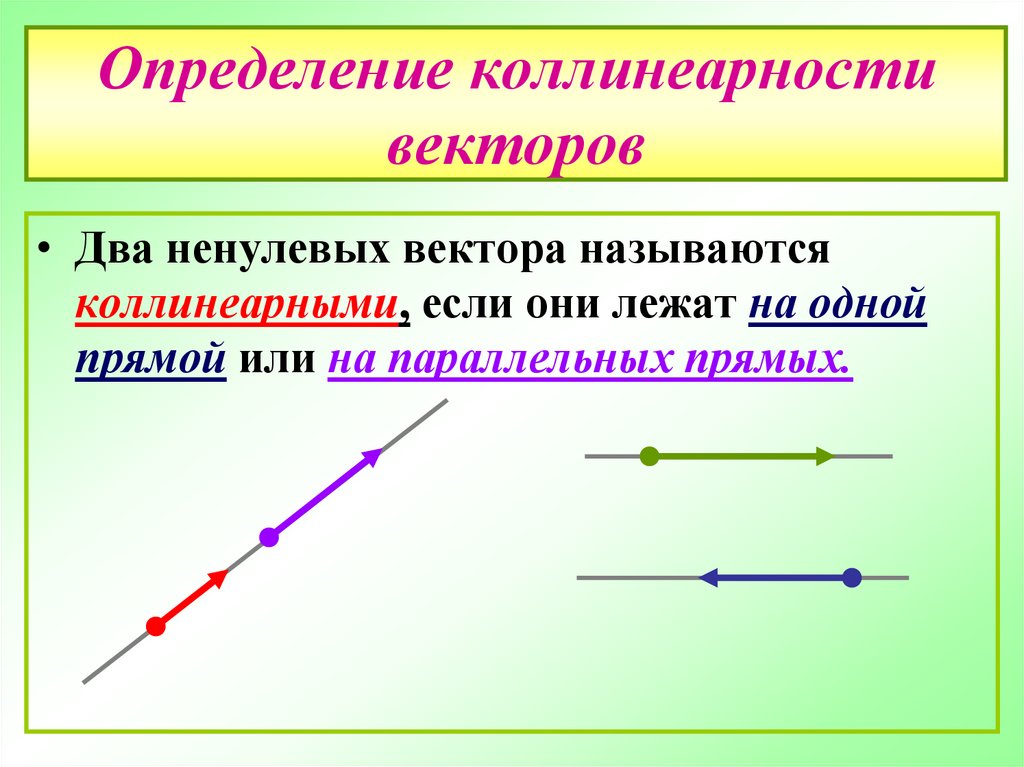
10. Определение коллинеарности векторов

• Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых.

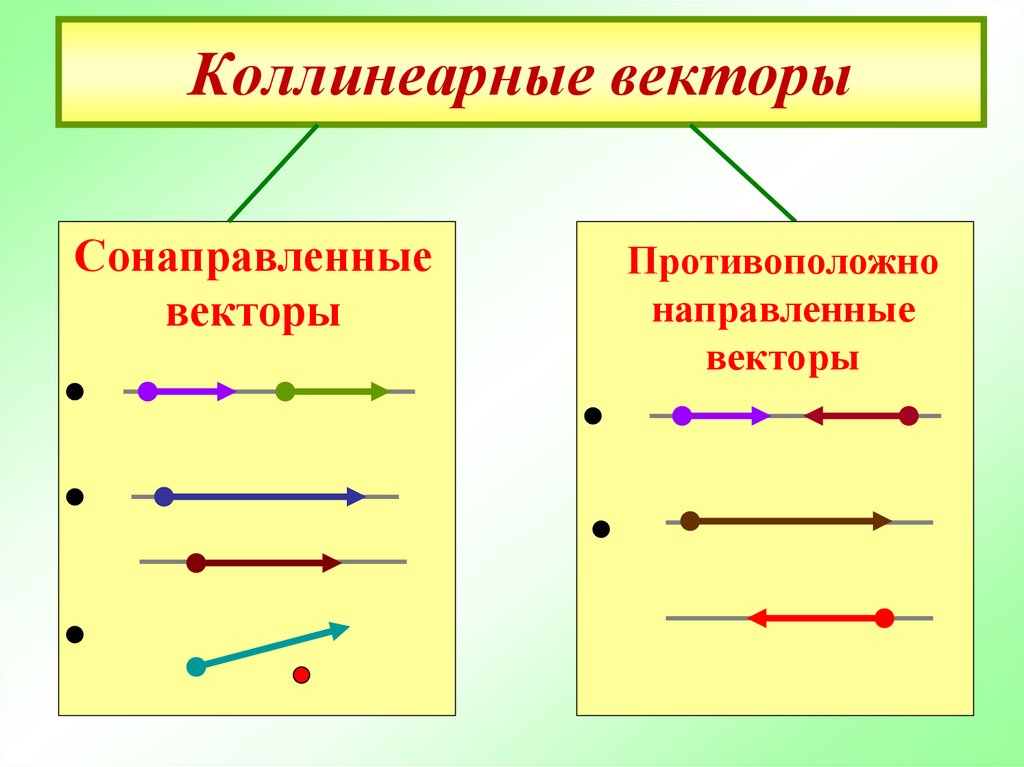
11. Коллинеарные векторы

Сонаправленные
векторы
Противоположно
направленные
векторы

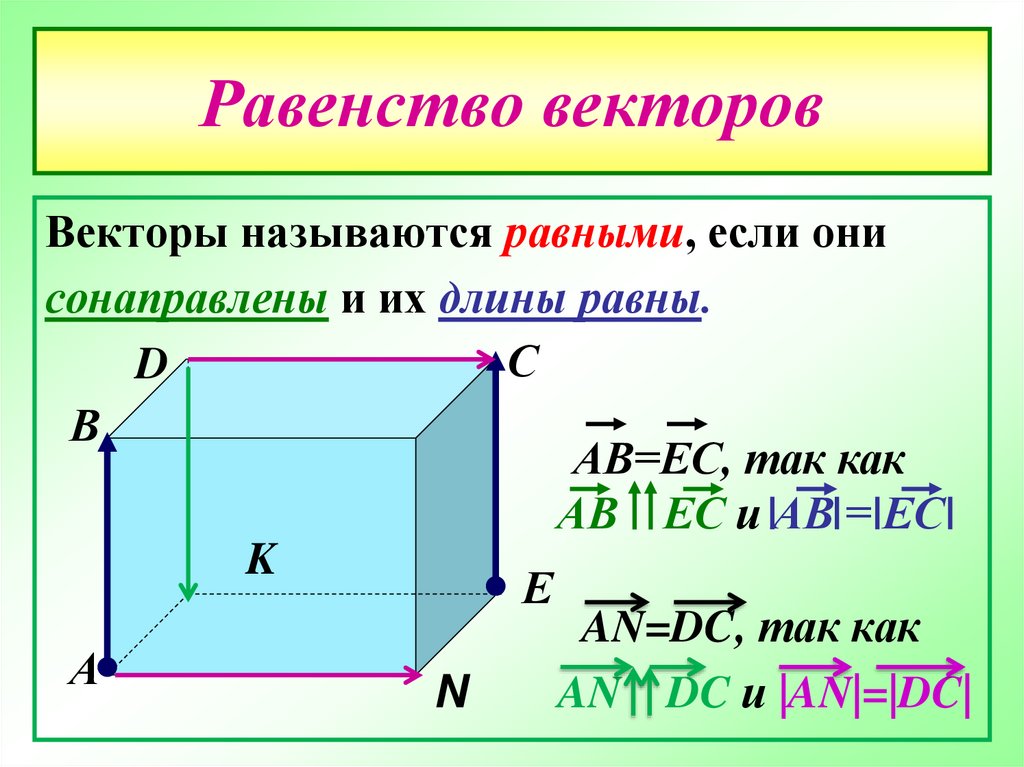
12. Равенство векторов

Векторы называются равными, если они
сонаправлены и их длины равны.
С
D
В
АВ=ЕС, так как
АВ ЕС и АВ = ЕС
K
Е
AN=DC, так как
А
N
AN DC и |AN|=|DC|

13. Какие векторы на рисунке сонаправленные? Какие векторы на рисунке противоположно направленные? Найти длины векторов АВ; ВС;

СС1.
3 см
D1 5 см
A1
В1
9 см
9 см
C1
D
A
5 см
C
3 см
B

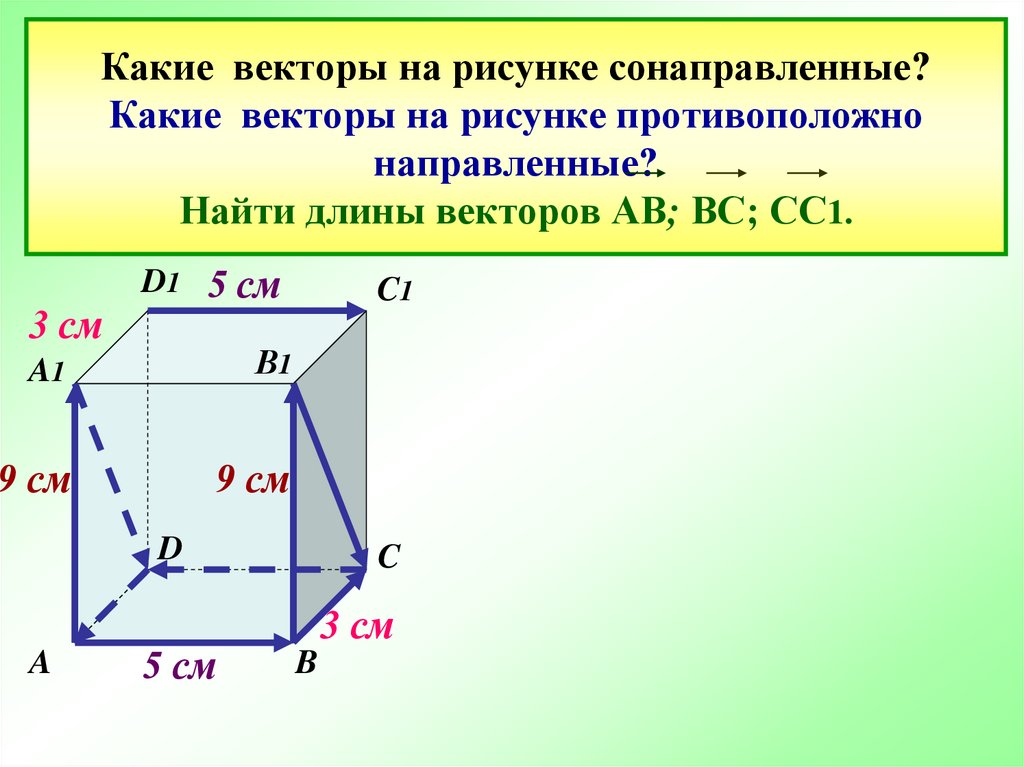
14. Какие векторы на рисунке сонаправленные? Какие векторы на рисунке противоположно направленные? Найти длины векторов АВ; ВС;

СС1.
Сонаправленные векторы:
D1 5 см
C1
AA1 BB1, A1D B1C
3 см
AB D1C1
В1
A1
Противоположно-направленные:
9 см
9 см
CD
D
A
5 см
C
D1C1, CD AB,
DA BC
3 см АВ = 5 см; ВС = 3 см; ВВ1 = 9 см.
B

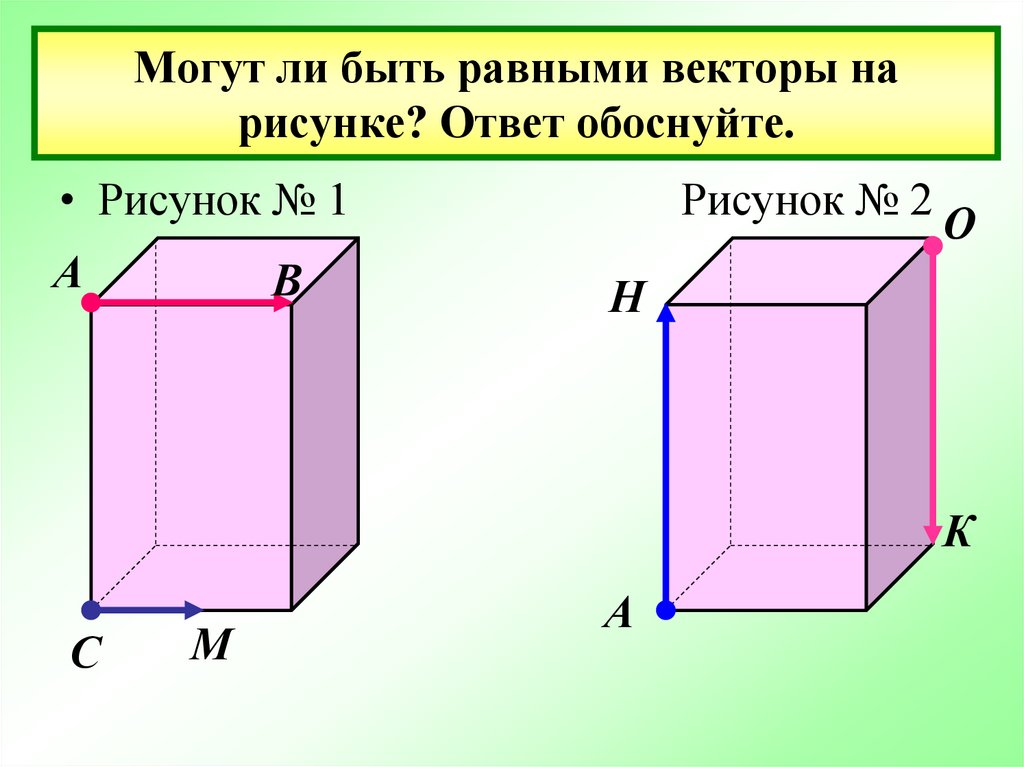
15. Могут ли быть равными векторы на рисунке? Ответ обоснуйте.

• Рисунок № 1
А
В
Рисунок № 2
О
Н
К
С
М
А

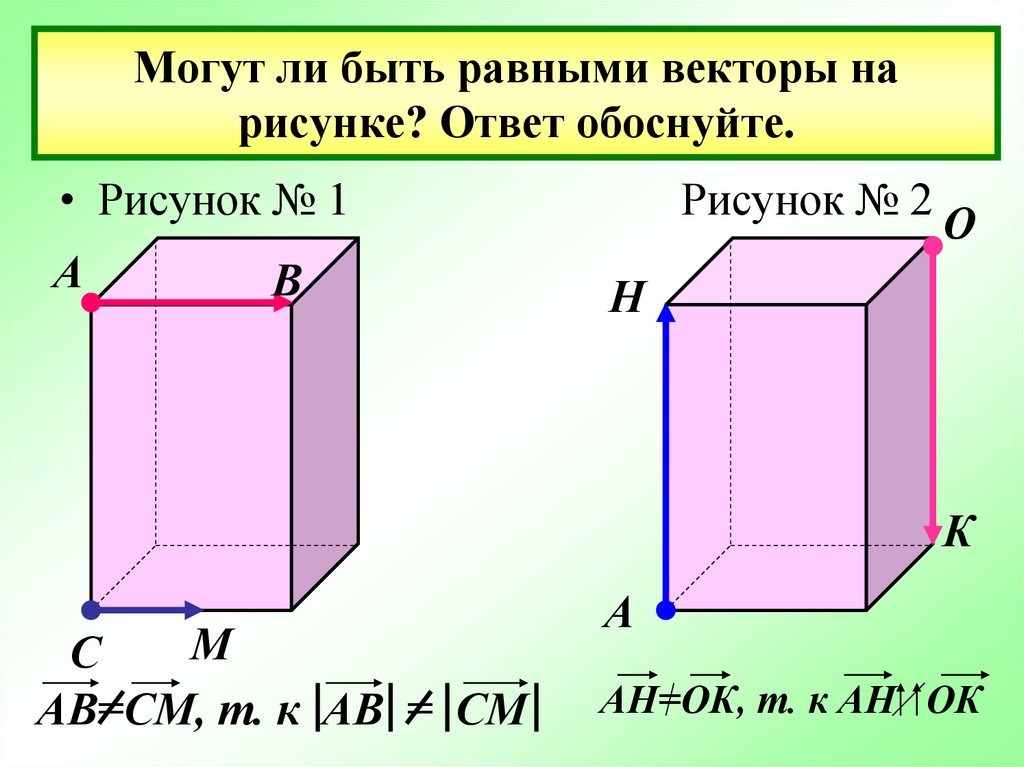
16. Могут ли быть равными векторы на рисунке? Ответ обоснуйте.

• Рисунок № 1
А
В
Рисунок № 2
О
Н
К
М
С
АВ=СМ, т. к АВ = СМ
А
АН=ОК, т. к АН ОК

17. Доказать, что от любой точки пространства можно отложить вектор, равный данному, и притом только один

Дано: а, М.
Доказать: в = а, М в, единственный.
Э
М
а
Проведем через вектор а и точку
М плоскость.
В этой плоскости построим
МК = а.
Из теоремы о параллельности
прямых следует МК = а и М МК.
Э
К
Доказательство:

18. Решение задач

№1
М
В1
А1
К
С1
Д1
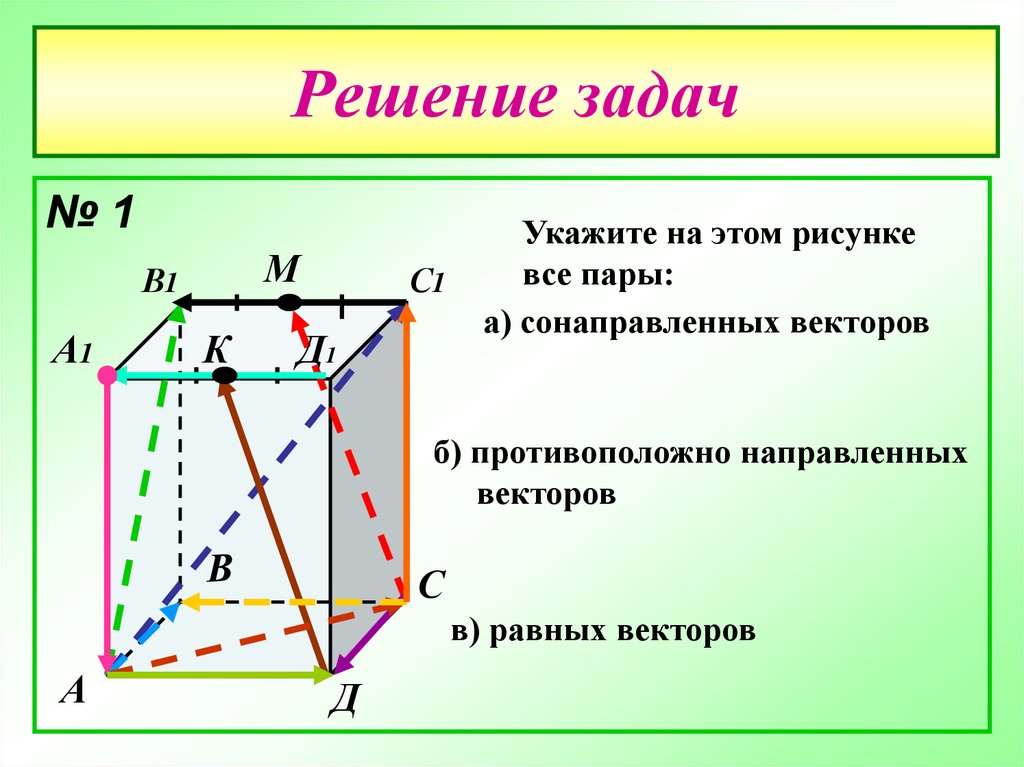
Укажите на этом рисунке
все пары:
а) сонаправленных векторов
б) противоположно направленных
векторов
С
в) равных векторов
А
Д

19. Решение задач

№1
М
В1
А1
К
С1
Д1
Укажите на этом рисунке
все пары:
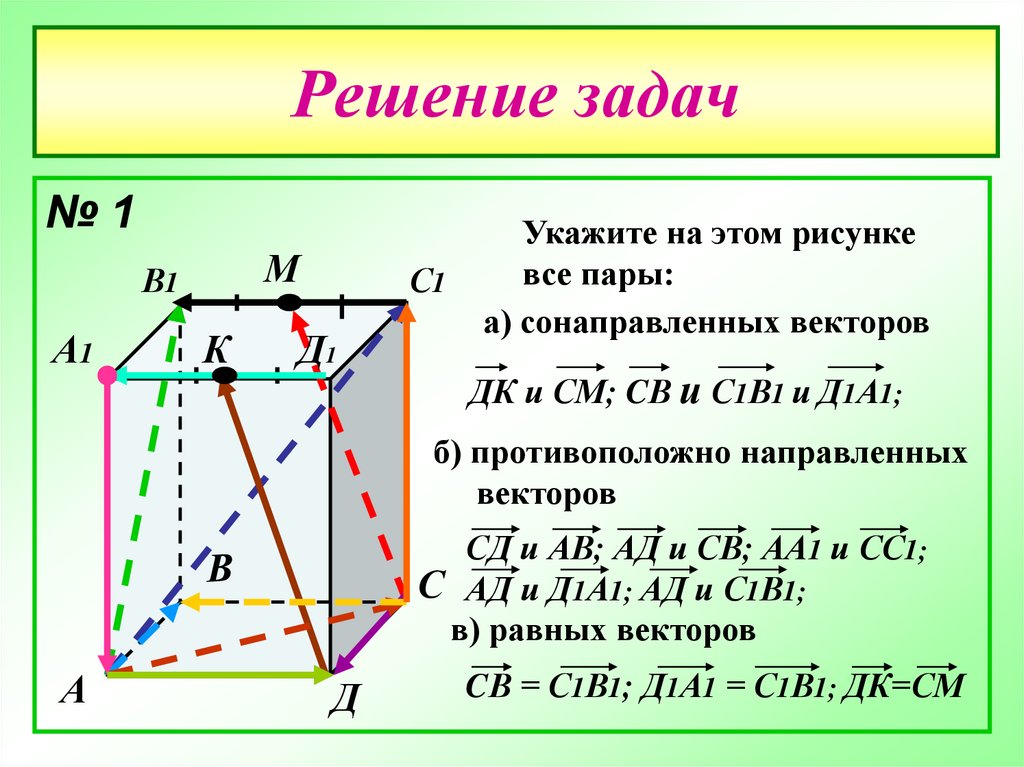
а) сонаправленных векторов
ДК и СМ; CВ и С1В1 и Д1А1;
б) противоположно направленных
векторов
СД и АВ; АД и СВ; АА1 и СС1;
С АД и Д1А1; АД и С1В1;
в) равных векторов
А
Д
CВ = С1В1; Д1А1 = С1В1; ДК=СМ

20. Решение задач

№2
М
В1
А1
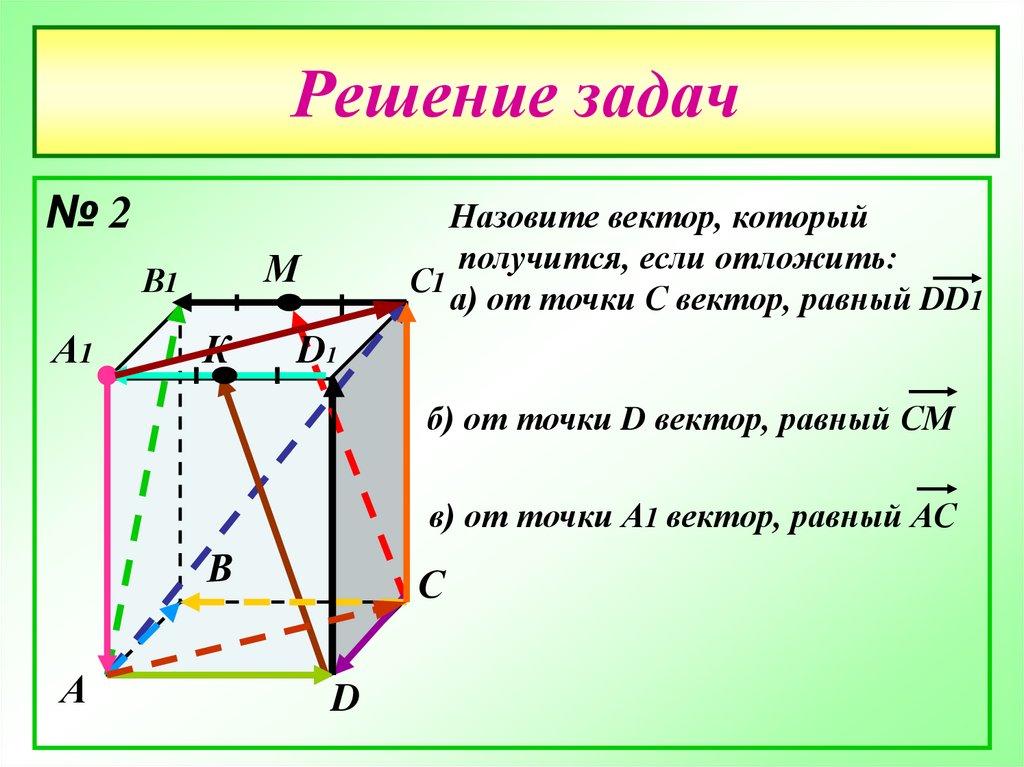
Назовите вектор, который
получится, если отложить:
С1
а) от точки С вектор, равный DD1
К
D1
б) от точки D вектор, равный СМ
в) от точки А1 вектор, равный АС
С
А
D

21. Решение задач

№2
М
В1
А1
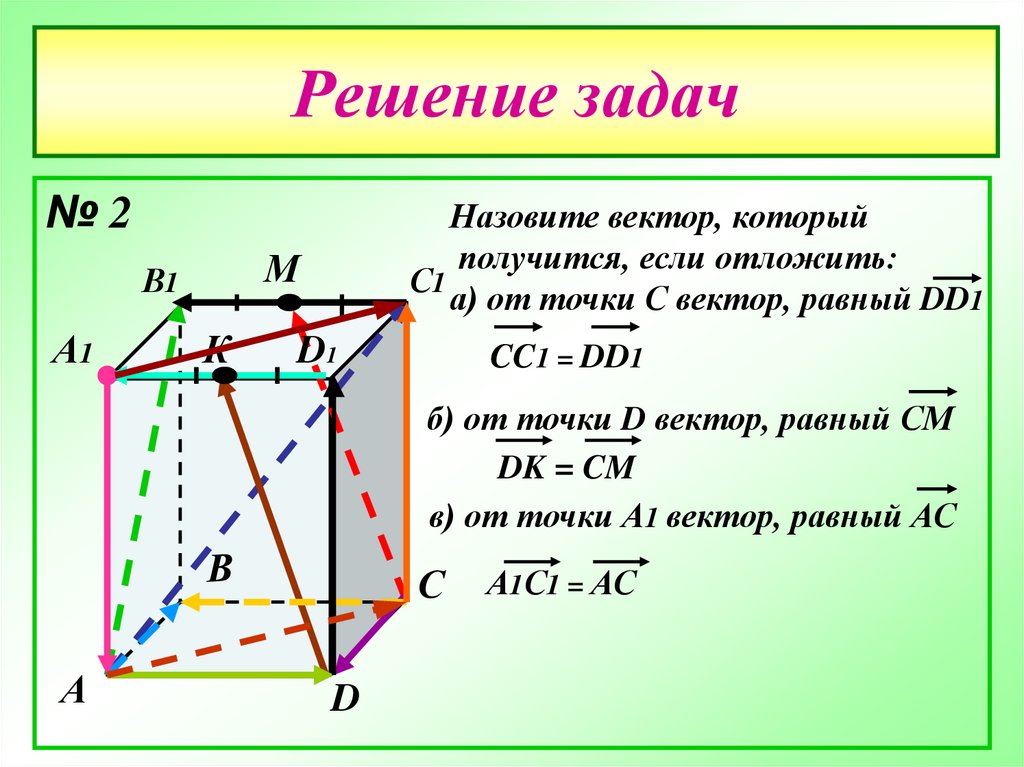
Назовите вектор, который
получится, если отложить:
С1
а) от точки С вектор, равный DD1
К
D1
CC1 = DD1
б) от точки D вектор, равный СМ
DK = CM
в) от точки А1 вектор, равный АС
С
А
D
А1С1 = АС

22.

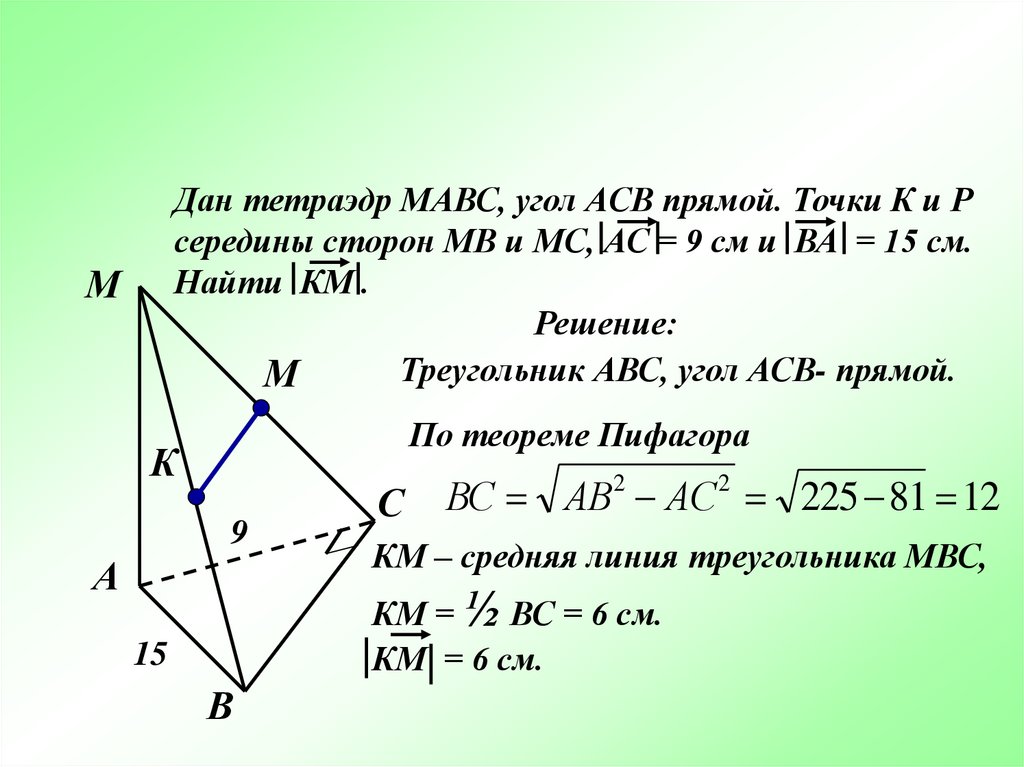
Дан тетраэдр МАВС, угол АСВ прямой. Точки К и Р
середины сторон МВ и МС, АС = 9 см и ВА = 15 см.
Найти КМ .
Решение:
Треугольник АВС, угол АСВ- прямой.
М
М
По теореме Пифагора
К
9
А
С
ВС АВ2 АС 2 225 81 12
КМ – средняя линия треугольника МВС,
КМ = ½ ВС = 6 см.
КМ = 6 см.
15
В

23. Физические величины

Скорость v
Ускорение а
Перемещение s
Сила F

24. Электрическое поле Электрическое поле, создаваемое в пространстве зарядами, характеризуется в каждой точке пространства

вектором
напряженности электрического
поля.
На рис. изображены
векторы напряженности
электрического поля
положительного
точечного заряда.

25. Магнитное поле

Электрический ток, т.е.
направленное движение
зарядов, создает в
пространстве магнитное поле,
которое характеризуется в
каждой точке пространства
вектором магнитной индукции.
На рис. изображены
векторы магнитной
индукции магнитного
поля прямого
проводника с током.

26.

Посмотрите видеофильм «Вектор
в пространстве» по ссылке
https://www.youtube.com/watch?v=p
5Q7im3qtzY