Похожие презентации:
Понятие вектора. Равенство векторов
1. Понятие вектора. Равенство векторов.
Тема урокаПонятие вектора.
Равенство векторов.
2. Цели урока
• Знать: определение вектора впространстве и связанные с
ним понятия; равенство
векторов.
• Уметь: решать задачи по
данной теме.
3. Понятие вектора появилось в 19 веке в работах математиков Г. Грассмана У. Гамильтона
4. Современная символика для обозначения вектора r была введена в 1853 году французским математиком О. Коши.
5.
ЗаданиеЗаписать все термины по теме «Векторы
на плоскости».
Вектор
Нулевой вектор
Длина вектора
Коллинеарные векторы
Сонаправленные векторы
Противоположно направленные
векторы
Равенство векторов
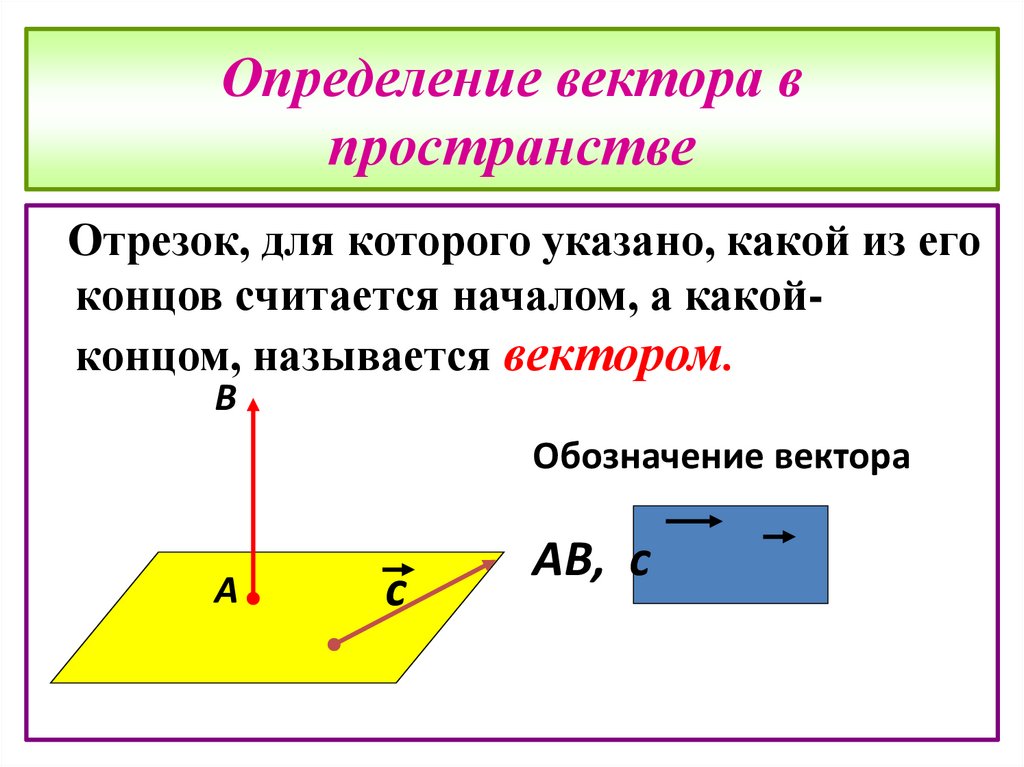
6. Определение вектора в пространстве
Отрезок, для которого указано, какой из егоконцов считается началом, а какойконцом, называется вектором.
В
Обозначение вектора
А
с
АВ, с
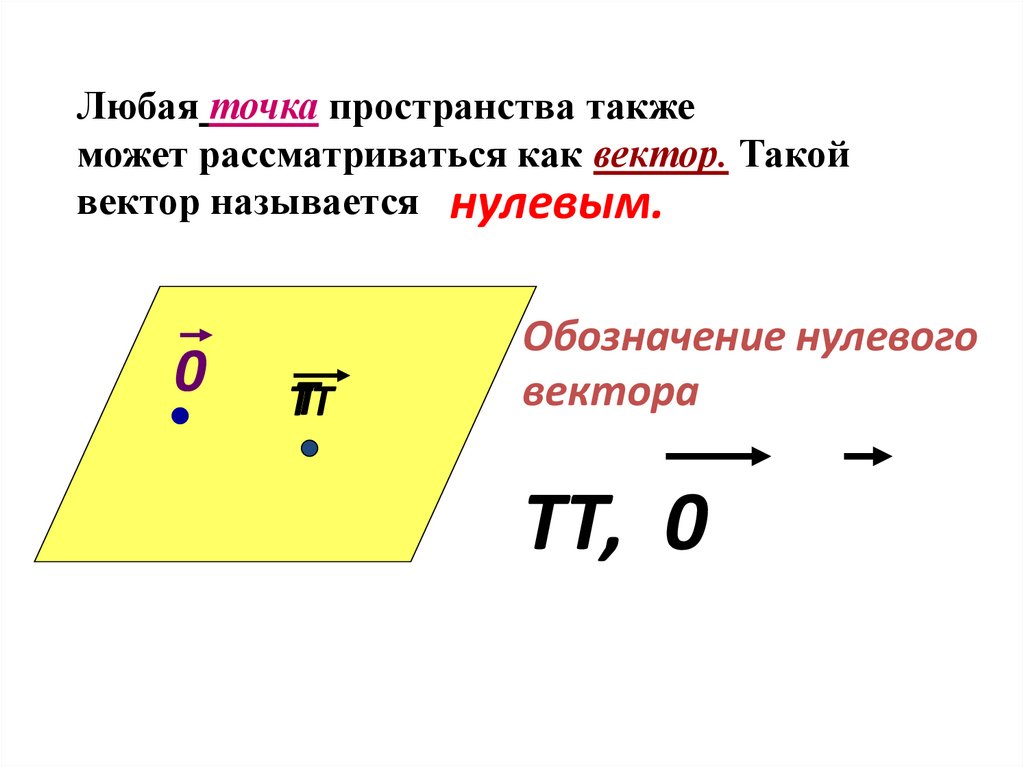
7. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется
нулевым.0
Т
ТТ
Обозначение нулевого
вектора
ТТ, 0
8. Длина ненулевого вектора
• Длиной вектора АВ называется длинаотрезка АВ.
• Длина вектора АВ (вектора а)
обозначается так:
АВ , а
• Длина нулевого вектора считается равной
нулю:
0 =0
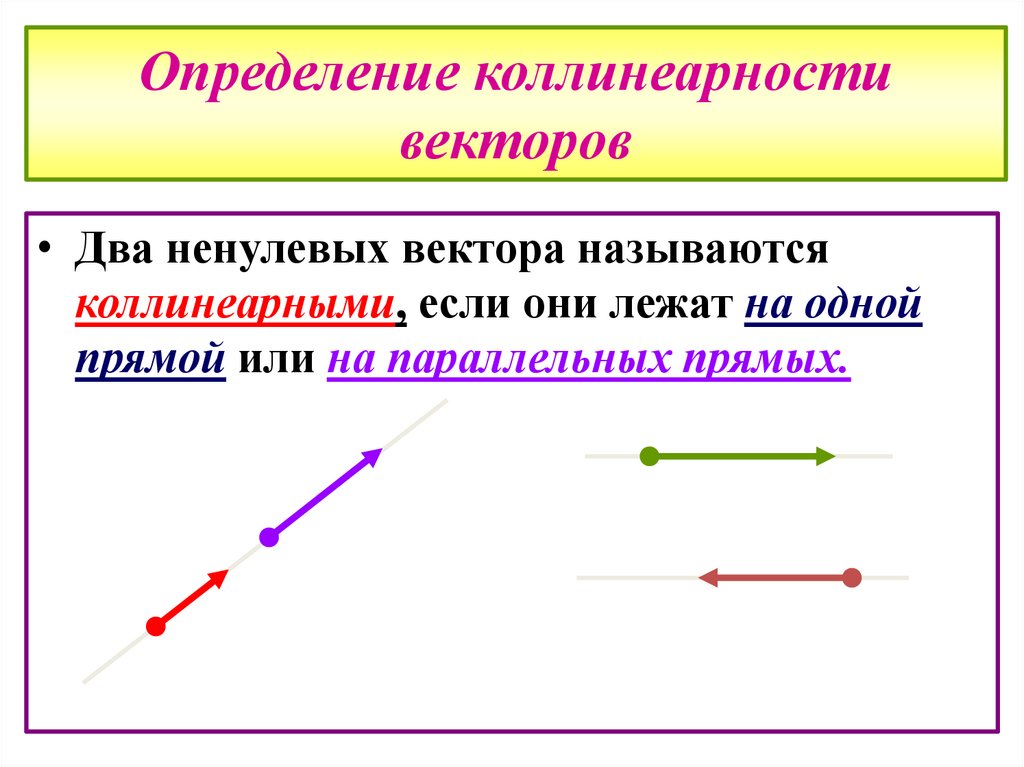
9. Определение коллинеарности векторов
• Два ненулевых вектора называютсяколлинеарными, если они лежат на одной
прямой или на параллельных прямых.
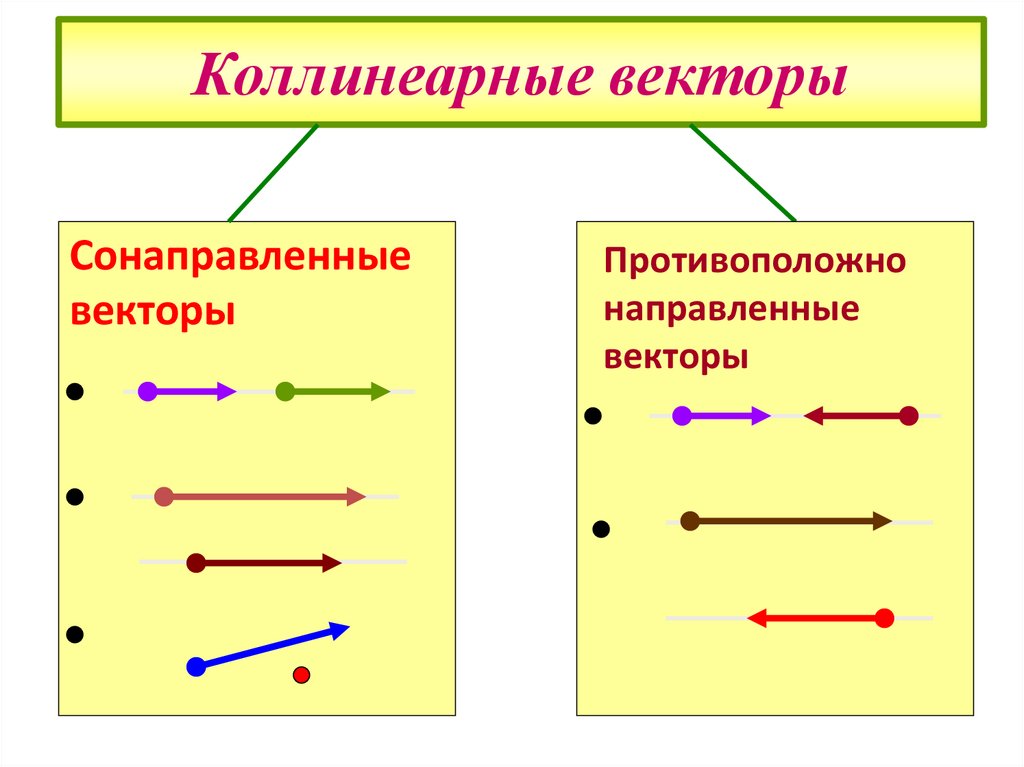
10. Коллинеарные векторы
Сонаправленныевекторы
Противоположно
направленные
векторы
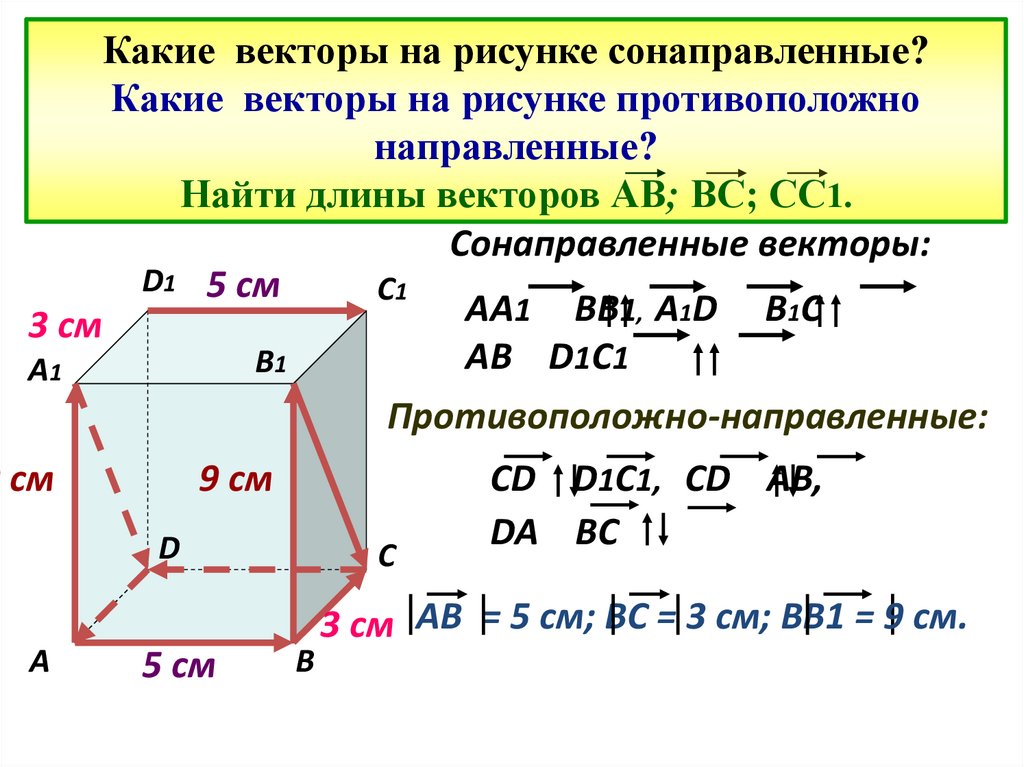
11. Какие векторы на рисунке сонаправленные? Какие векторы на рисунке противоположно направленные? Найти длины векторов АВ; ВС;
СС1.Сонаправленные векторы:
D1 5 см
C1
AA1 BB1, A1D B1C
3 см
AB D1C1
В1
A1
Противоположно-направленные:
9 см
9 см
D
A
5 см
C
B
CD D1C1, CD AB,
DA BC
3 см АВ = 5 см; ВС = 3 см; ВВ1 = 9 см.
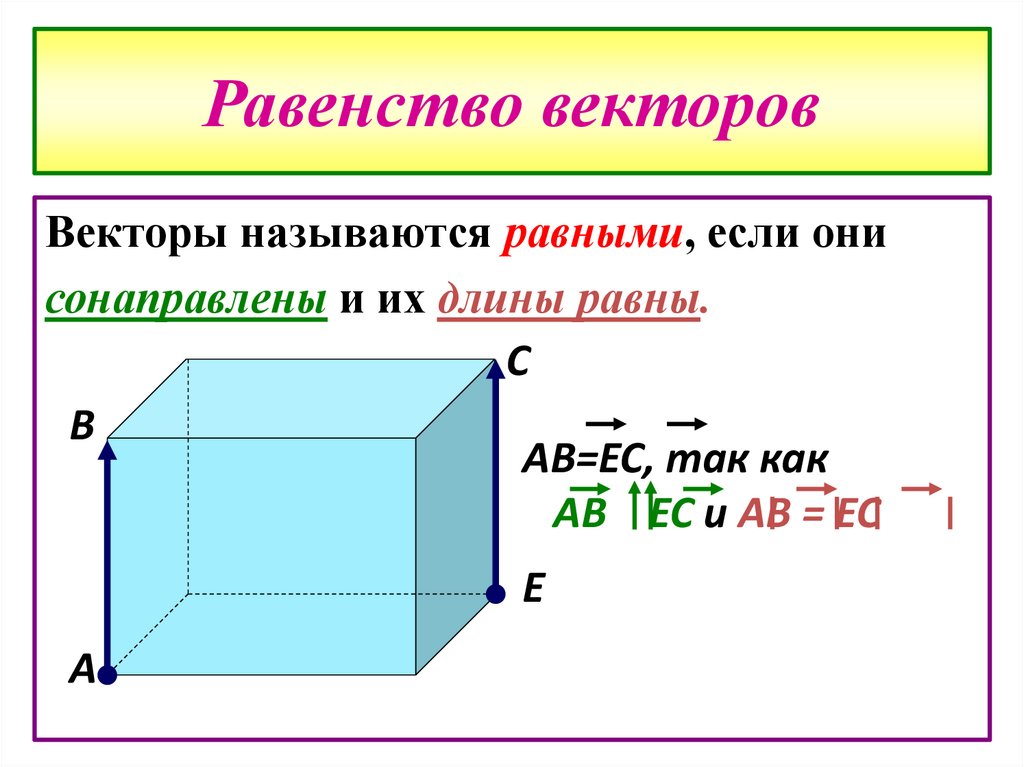
12. Равенство векторов
Векторы называются равными, если онисонаправлены и их длины равны.
С
В
АВ=ЕС, так как
АВ ЕС и АВ = ЕС
Е
А
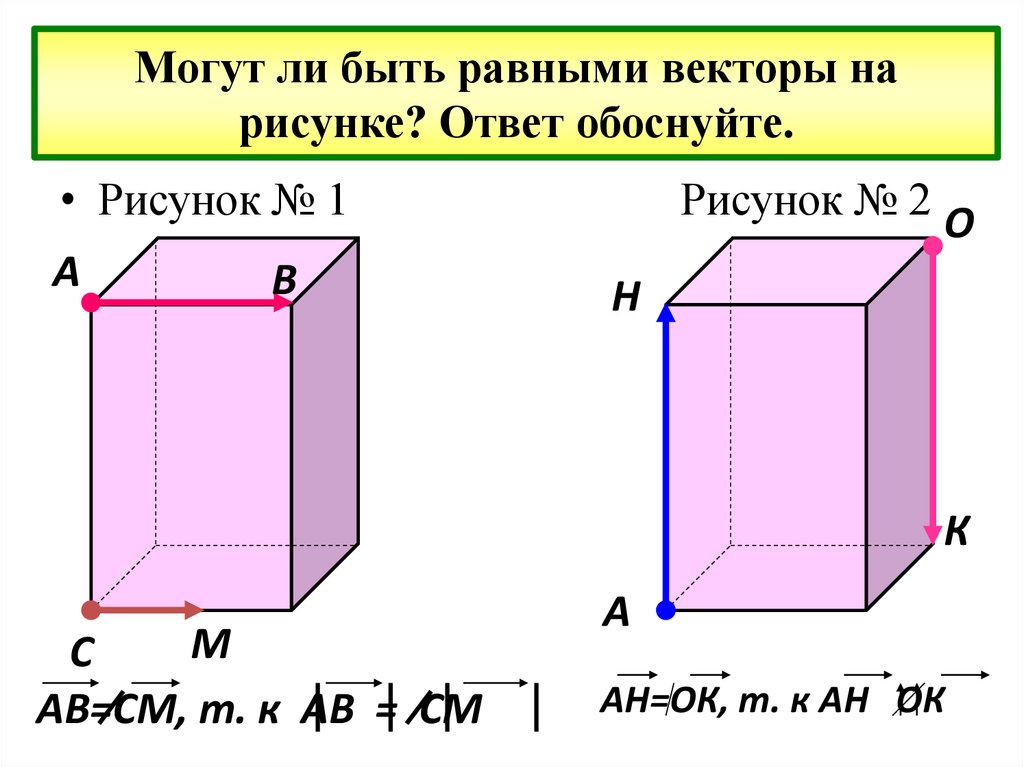
13. Могут ли быть равными векторы на рисунке? Ответ обоснуйте.
• Рисунок № 1А
В
Рисунок № 2
О
Н
К
М
С
АВ=СМ, т. к АВ = СМ
А
АН=ОК, т. к АН ОК
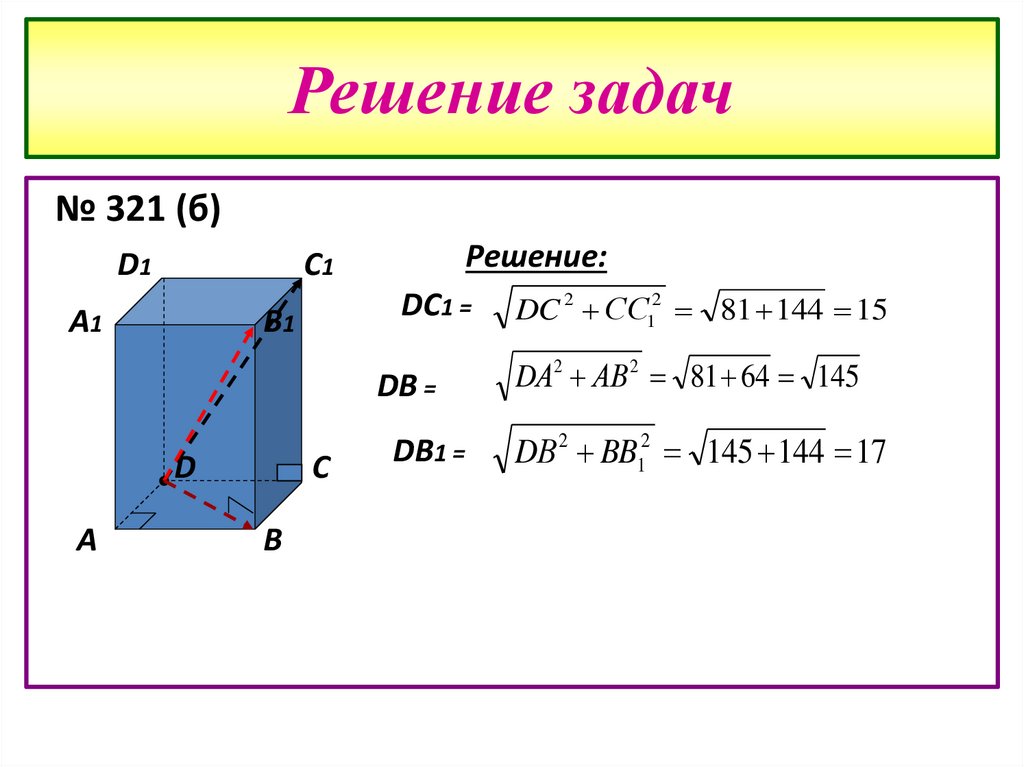
14. Решение задач
№ 321 (б)D1
Решение:
C1
A1
DC1 =
B1
DB =
D
A
C
B
DB1 =
DC 2 СС12 81 144 15
DА2 АВ 2 81 64 145
DВ 2 BB12 145 144 17
15. Решение задач
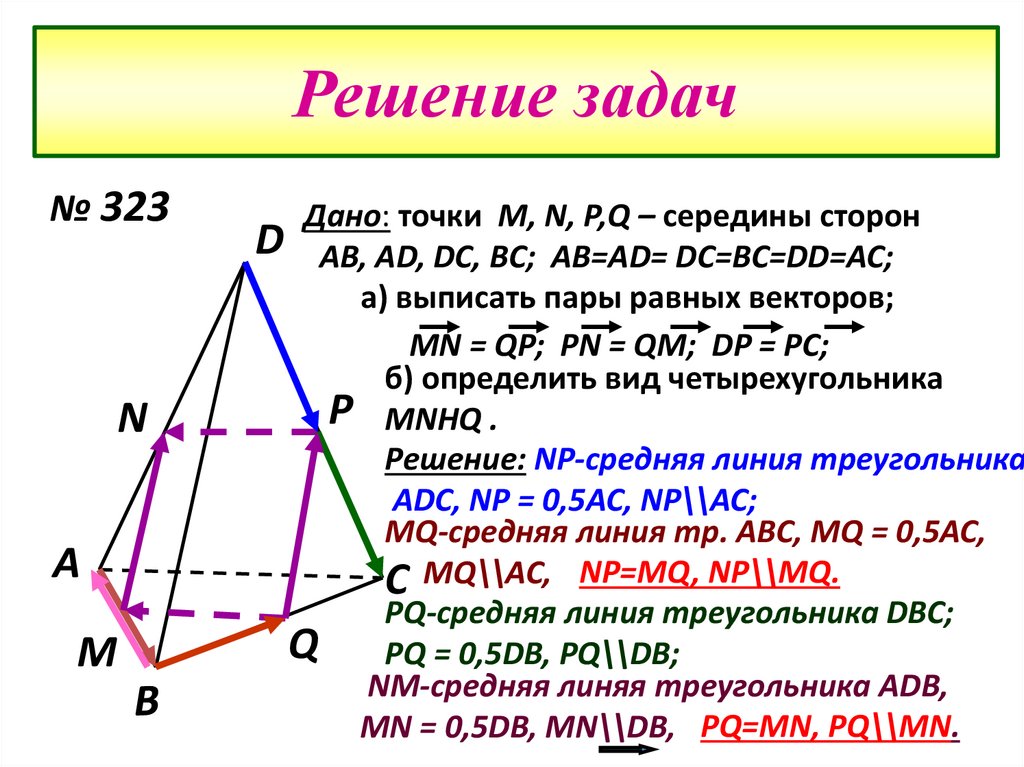
№ 323N
А
М
Дано: точки М, N, P,Q – середины сторон
D AB, AD, DC, BC; AB=AD= DC=BC=DD=AC;
а) выписать пары равных векторов;
MN = QP; PN = QM; DP = PC;
б) определить вид четырехугольника
Р MNHQ .
Решение: NP-средняя линия треугольника
ADC, NP = 0,5AC, NP\\AC;
MQ-средняя линия тр. ABC, MQ = 0,5AC,
С MQ\\AC, NP=MQ, NP\\MQ.
PQ-средняя линия треугольника DВC;
Q PQ = 0,5DB, PQ\\DB;
NM-средняя линяя треугольника ADB,
MN = 0,5DB, MN\\DB, PQ=MN, PQ\\MN.
16.
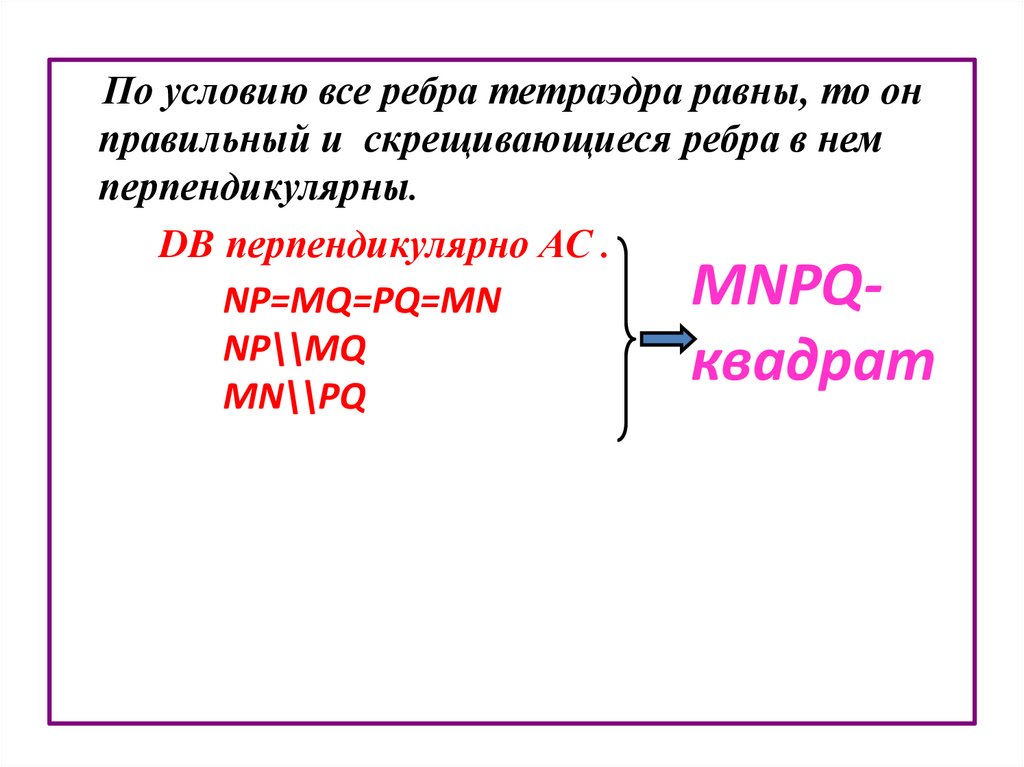
По условию все ребра тетраэдра равны, то онправильный и скрещивающиеся ребра в нем
перпендикулярны.
DB перпендикулярно АС .
MNPQNP=MQ=PQ=MN
NP\\MQ
квадрат
MN\\PQ






 Математика
Математика








