Похожие презентации:
Основные методы интегрирования
1.
Вычисление интегралов с помощью основныхсвойств неопределенного интеграла и
таблицы интегралов называется
непосредственным или элементарным
интегрированием.
2.
Вычислить интегралы:1
(2 sin x 6 3x )dx
2
3.
(2
sin
x
6
3
x
)
dx
2
2 sin x dx 6 dx 3 x dx
2
2 sin x dx 6 dx 3 x dx
2
3
x
2 cos x 6 x 3
C
3
4.
mx x
n
n
m
1
n
x n
x
5.
25
6
3
x
dx
x
dx
3 14
5 x dx
4
x 5 dx
12
7
4
x dx
3
x
5
dx
1
3
x
5
dx
6.
23x x x 2
dx
2
x
4
3
7.
3x 4 x 3 x 2dx
2
x
1
1
2
3 x x 2 2 dx
x
x
1
2
3 x dx x dx dx 2 x 2 dx
x
2
1
x
x
x3
ln x 2
C
2
1
2
x
2
3
x
ln x C
2
x
8.
32
2 x
x 2 1 sin 2 dx
9.
22 x
x 2 1 sin 2 dx
1
2 x
2 2
dx sin
dx
x 1
2
1
2arctgx (1 cos x)dx
2
1
1
2arctgx x sin x C
2
2
10.
( 5 sin x 6 x 5 x )dx4
8
5
(4 cos x x 6 x )dx
3x 2 5 x 3 2 x 7
dx
3
x
4
2
5x 4 x x 2
dx
4
x
11.
52 x
x 2 1 cos 2 dx
2
x
cos 2 x 2 dx
5
4
3
x
dx
2
sin x
2
3
2
x 1 5 x 4 dx
12.
Метод заменыформулой:
переменной
описывается
f ( x)dx f ( (t )) (t )dt
1
13.
Вычислить интегралы:1
x( x 1) dx
12
14.
x 1 tx t 1
x( x 1) dx x dx t 1 dt
12
dx dt
(t 1) t dt t dt t dt
12
12
13
t 13 t 14
( x 1)13 ( x 1)14
C
C
13 14
13
14
15.
2sin x cos x dx
4
16.
sin x t4
sin x cos x dx sin x dx t dt
cos x dx dt
dt
1 5
1
t dt t C sin 5 x C
5
5
4
17.
Пусть F(x) – некотораяпервообразная для функции f(x).
Тогда
1
f (kx b)dx k F (kx b) C
18.
Вычислить интегралы:1
3 xdx
3
19.
n 1x
x
dx
C
n 1
n
3 xdx 3 x dx
3
1
3
4
k 1
3
(3 x) 3 C
b 3
4
20.
21
4 x 3 dx
21.
1dx
ln
x
C
x
k 4 1
1
4 x 3 dx b 3 4 ln 4 x 3 C
22.
Пусть функции u(x) и v(x)определены и дифференцируемы на
промежутке Х и функция
u ( x) v( x)
имеет первообразную на этом
промежутке.
23.
Тогда функцияv ( x ) u ( x )
тоже имеет первообразную на
этом промежутке и справедлива
формула
u
(
x
)
v
(
x
)
dx
u
(
x
)
v
(
x
)
v
(
x
)
u
( x)dx
24.
Посколькуu ( x)dx du
v ( x) dx dv
То последнее равенство часто записывают в
виде:
u
dv
u
v
v
du
25.
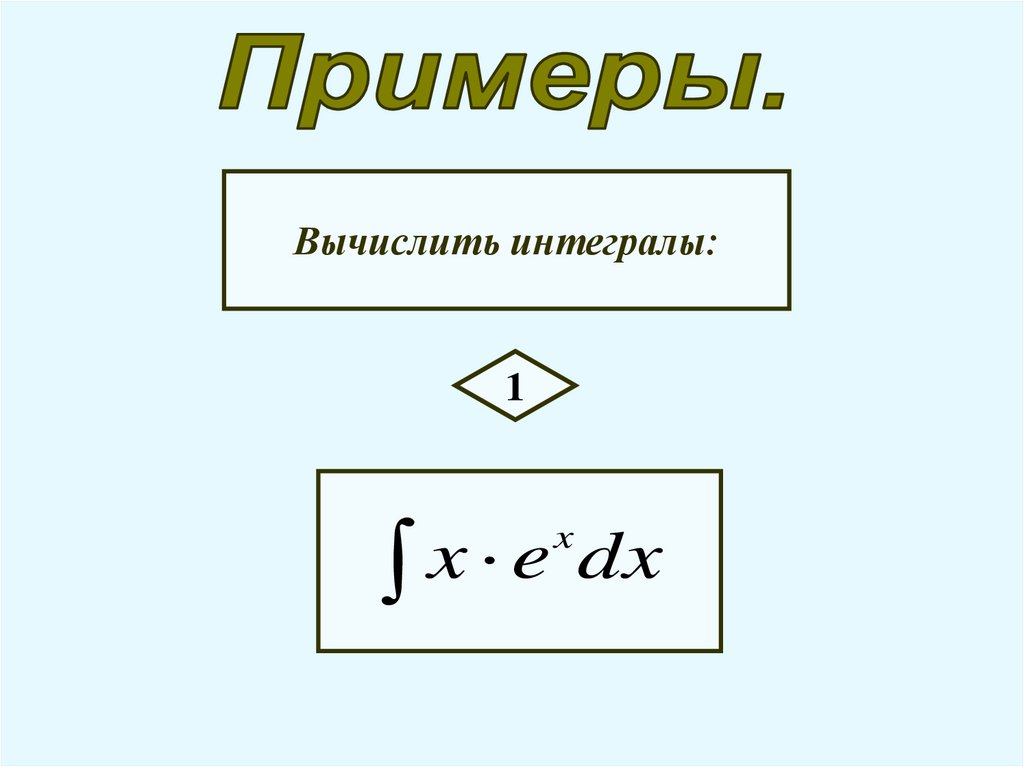
Вычислить интегралы:1
x e dx
x
26.
u xx e dx du dx
x
dv e dx
x
v e
x
x e e dx x e e C
x
x
x
x
27.
2ln xdx
28.
u ln x1
ln
xdx
du dx
x
dv dx
v x
x
x ln x dx x ln x x C
x
29.
3x cos xdx
2
30.
2u
x
dv cos xdx
2
x cos xdx du 2 xdx v sin x
x sin x 2 x sin xdx
2
u x dv sin xdx
du dx v cos x
x 2 sin x 2 x cos x 2 cos xdx
x sin x 2 x cos x 2 sin x C
2
31.
Можнопоказать,
что
формула
интегрирования по частям применима для
следующих типов интегралов:
x e dx
x sin mxdx
x cosmxdx
x ln xdx
n
n
ax
n
k
n
32.
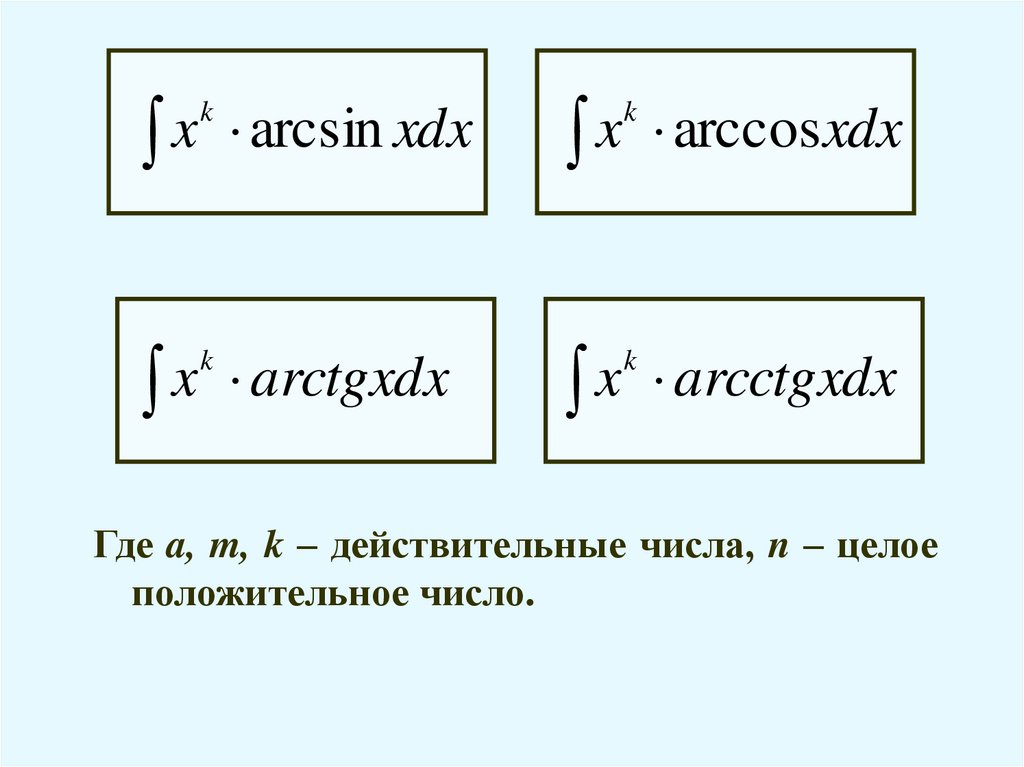
x arcsin xdxx arccosxdx
x arctgxdx
x arcctgxdx
k
k
k
k
Где a, m, k – действительные числа, n – целое
положительное число.



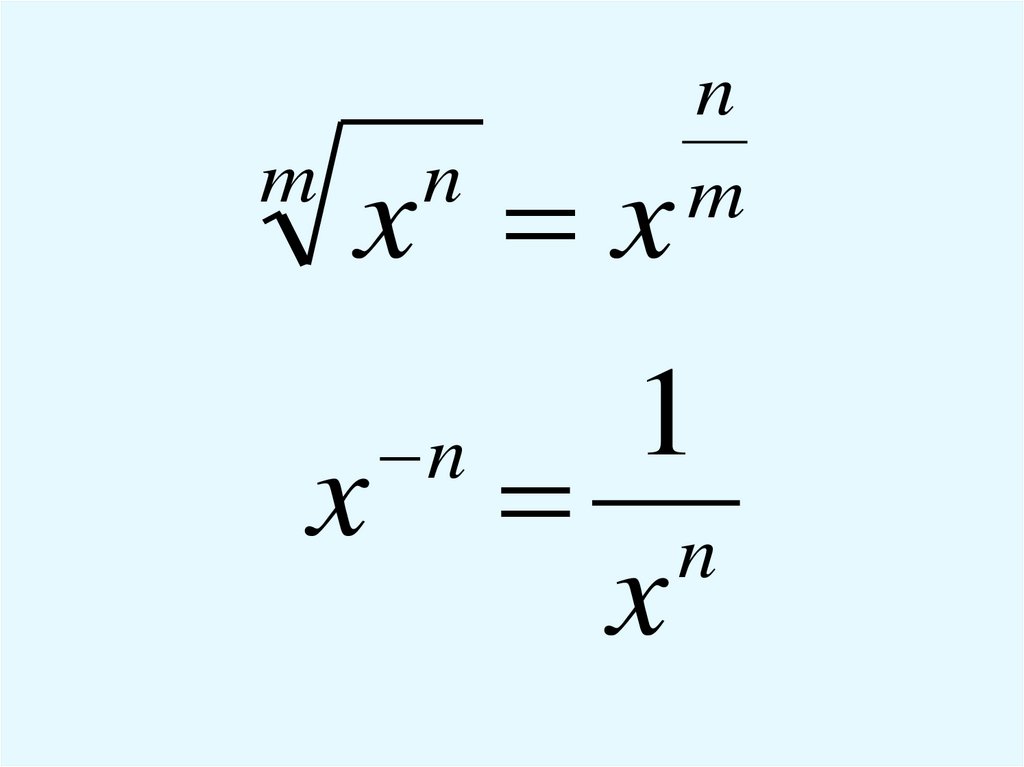



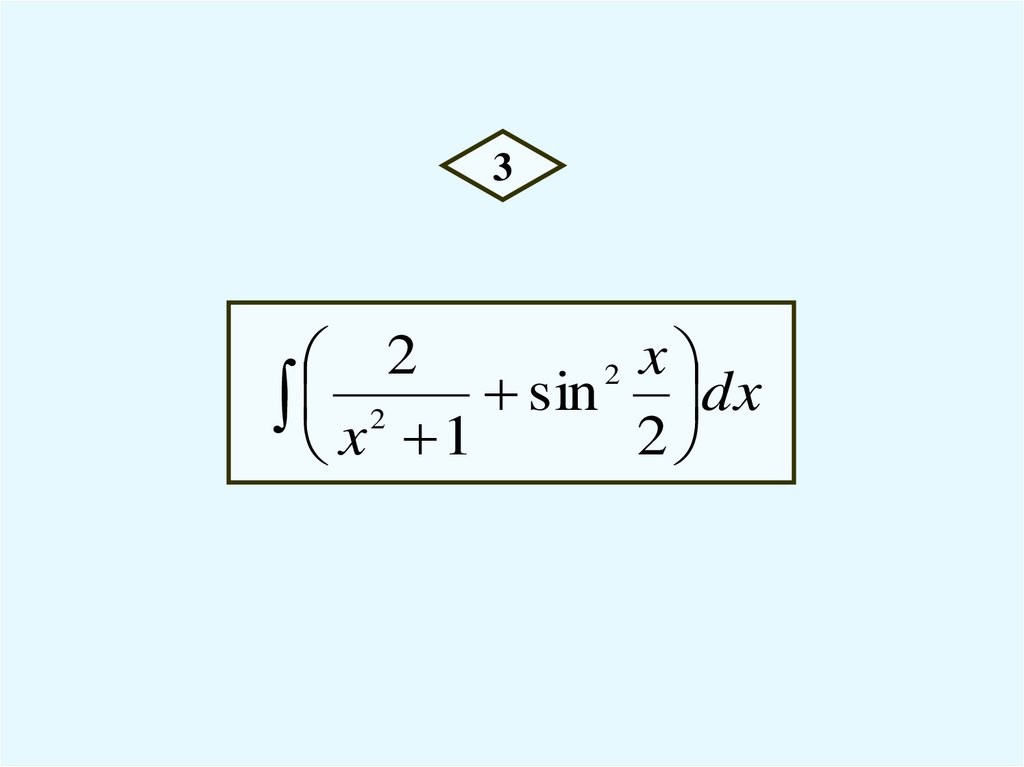
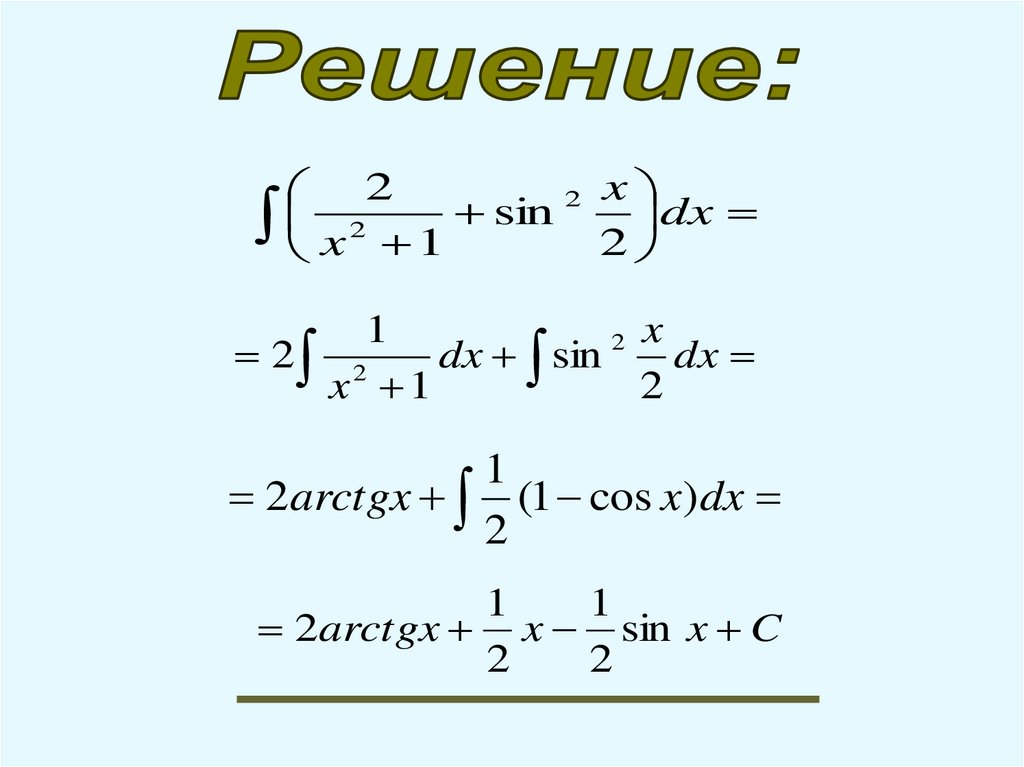

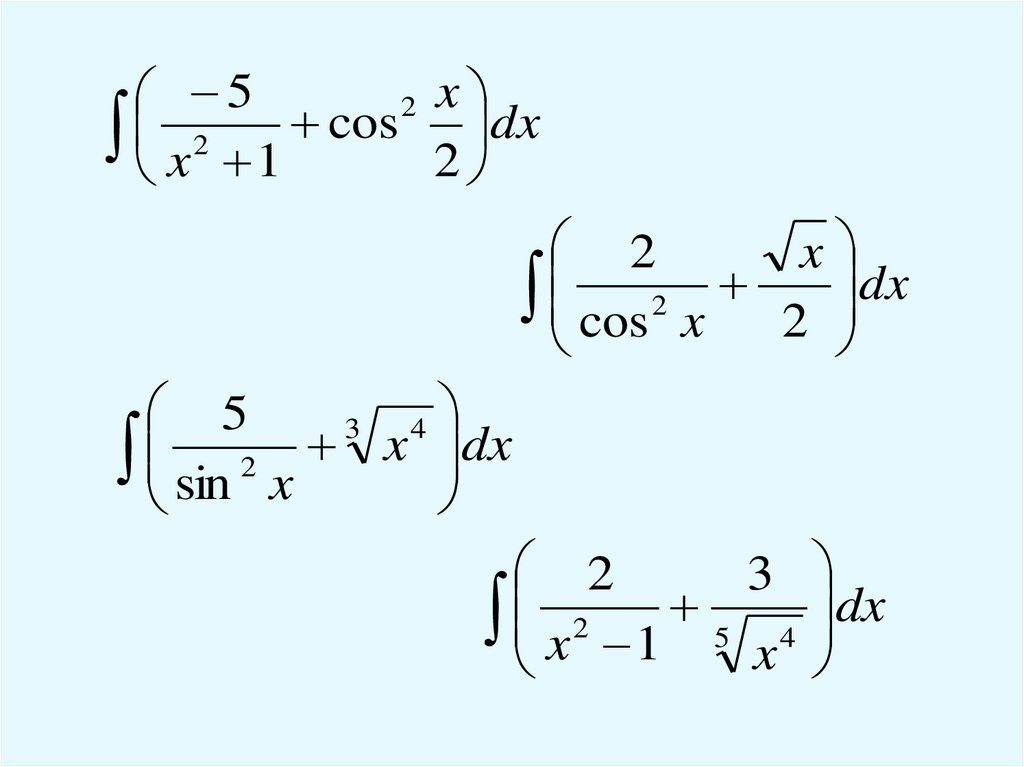







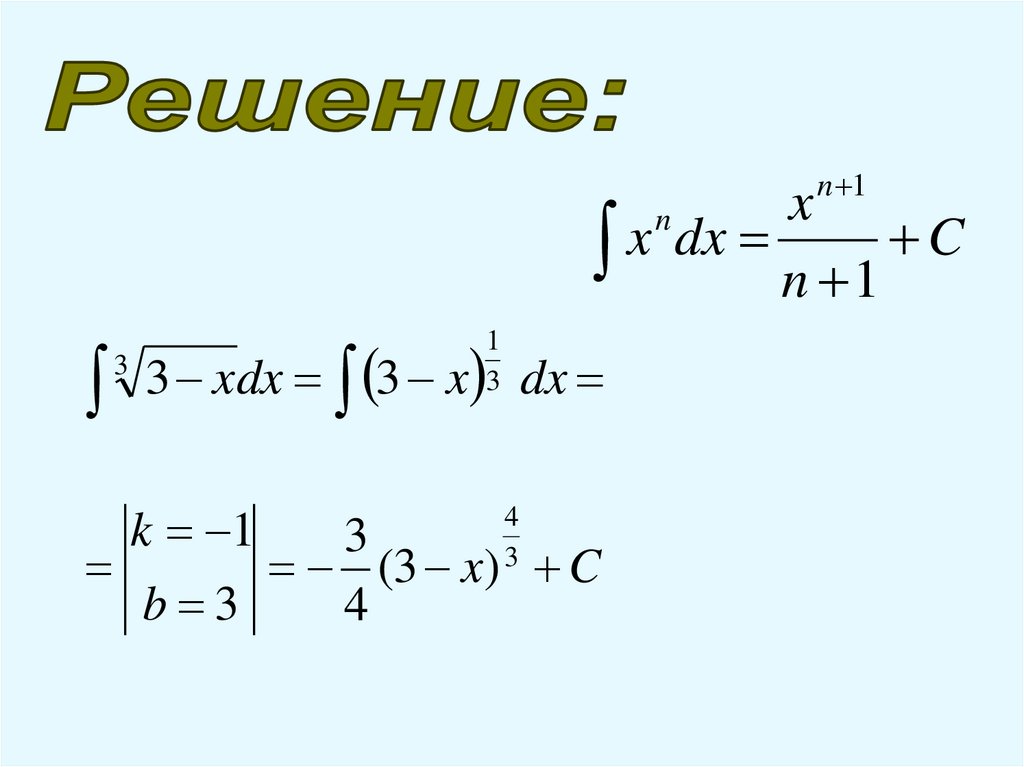
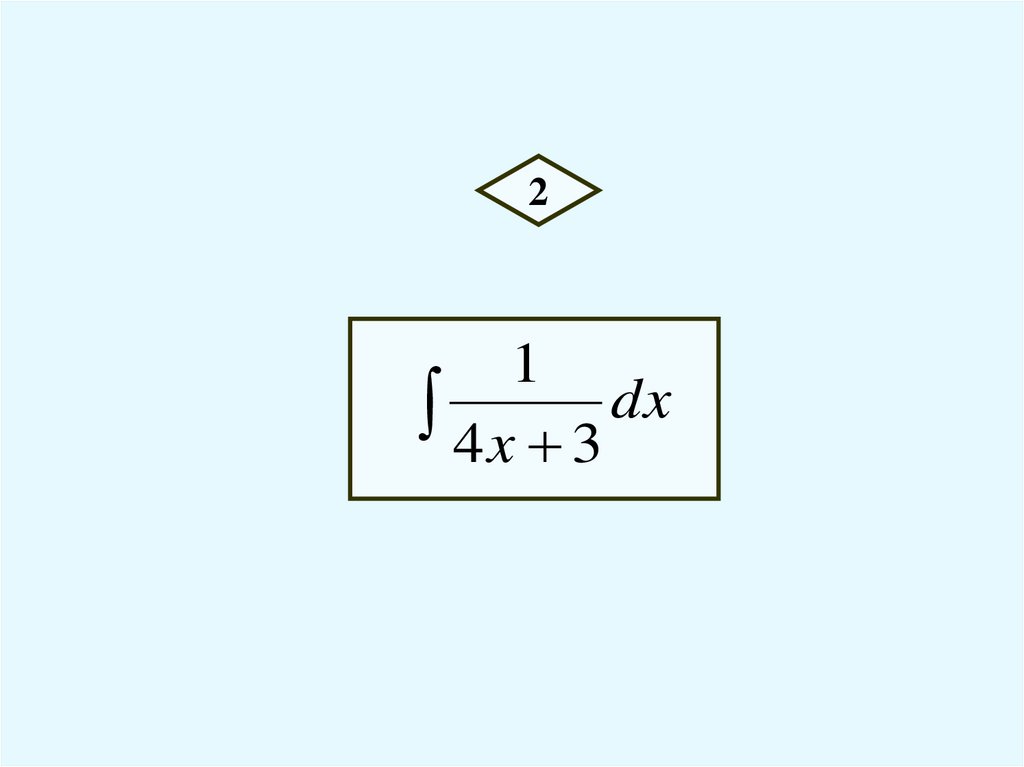
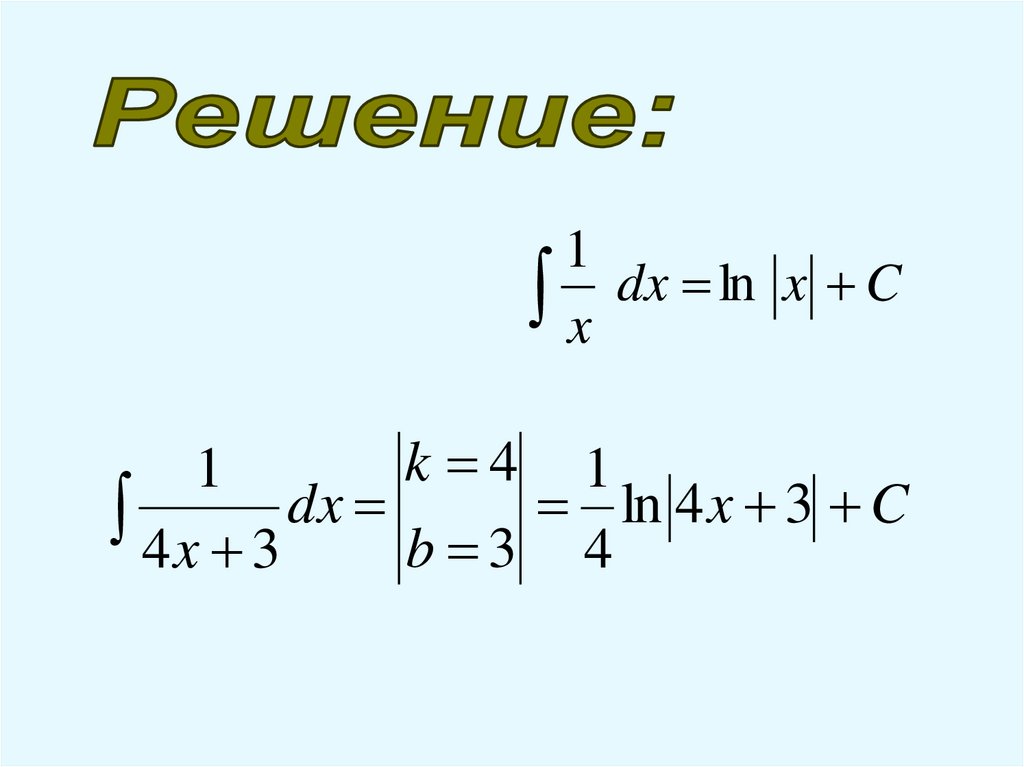




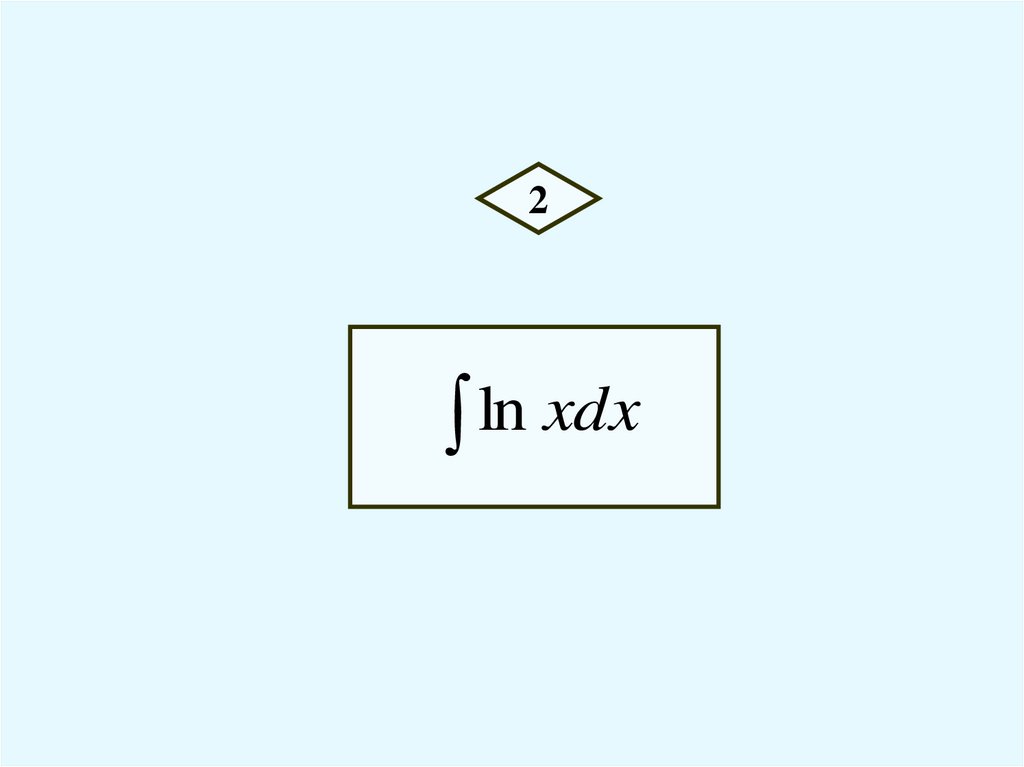
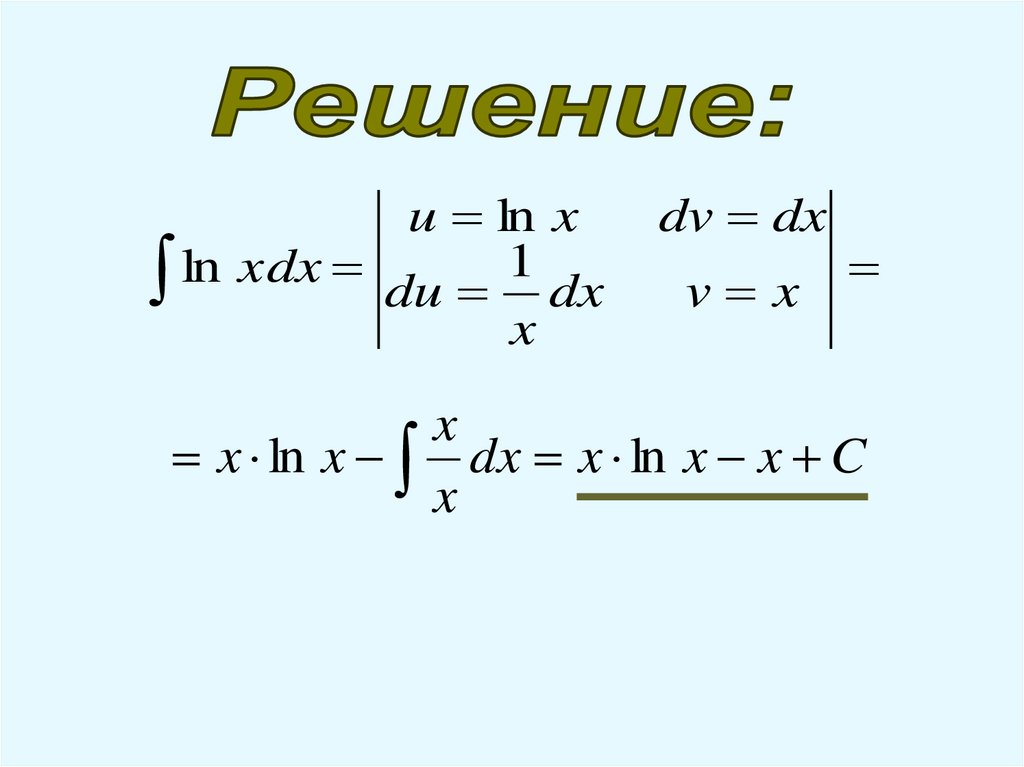
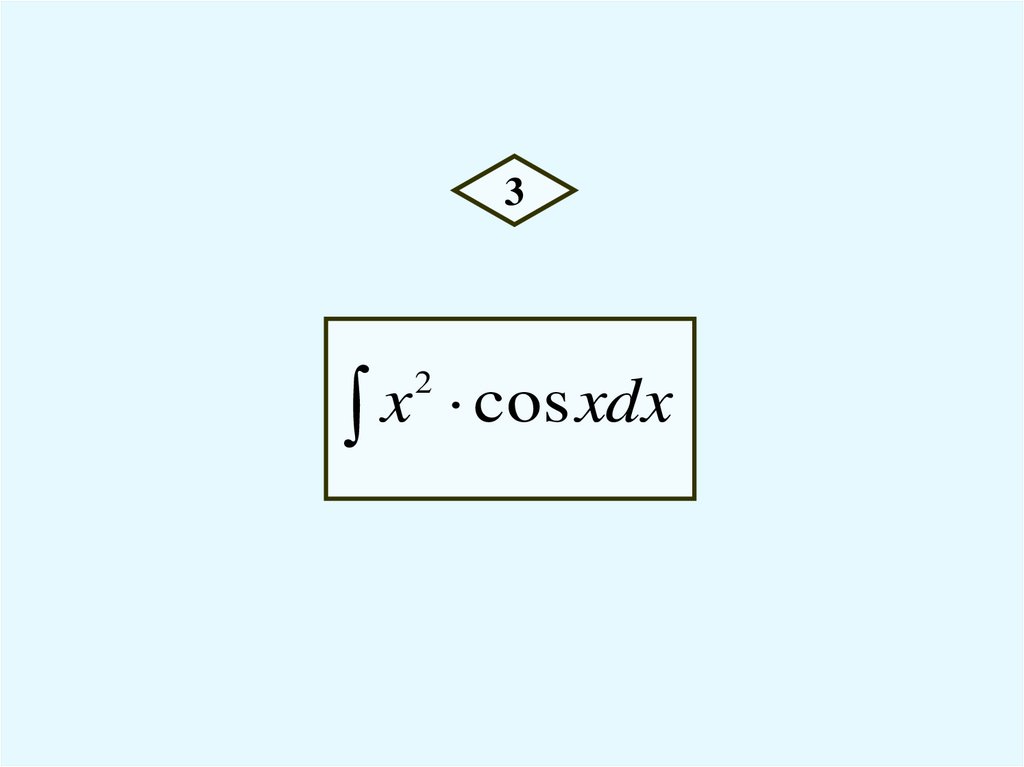


 Математика
Математика








