Теорема косинусов

1. Теорема косинусов

Теорема
(косинусов).
Квадрат
любой
стороны
треугольника равен сумме квадратов двух других сторон
без удвоенного произведения этих сторон на косинус угла
между ними, c2= a2 + b2 – 2ab cos C.
Доказательство: Обозначим АВ = с,
ВС = а, АС = b. Из вершины А
опустим перпендикуляр АD. Тогда
АD = b sin C, CD = b cos C, BD = a –
b cos C. По теореме Пифагора
имеем c2 = (a – b cos C)2 + (b sin C)2
= a2 – 2ab cos C + b2cos2C + b2sin2C
= a2 + b2 – 2ab cos C.
Самостоятельно рассмотрите случаи прямого и тупого угла С.

2. Упражнение 17

Докажите,
что
сумма
квадратов
диагоналей
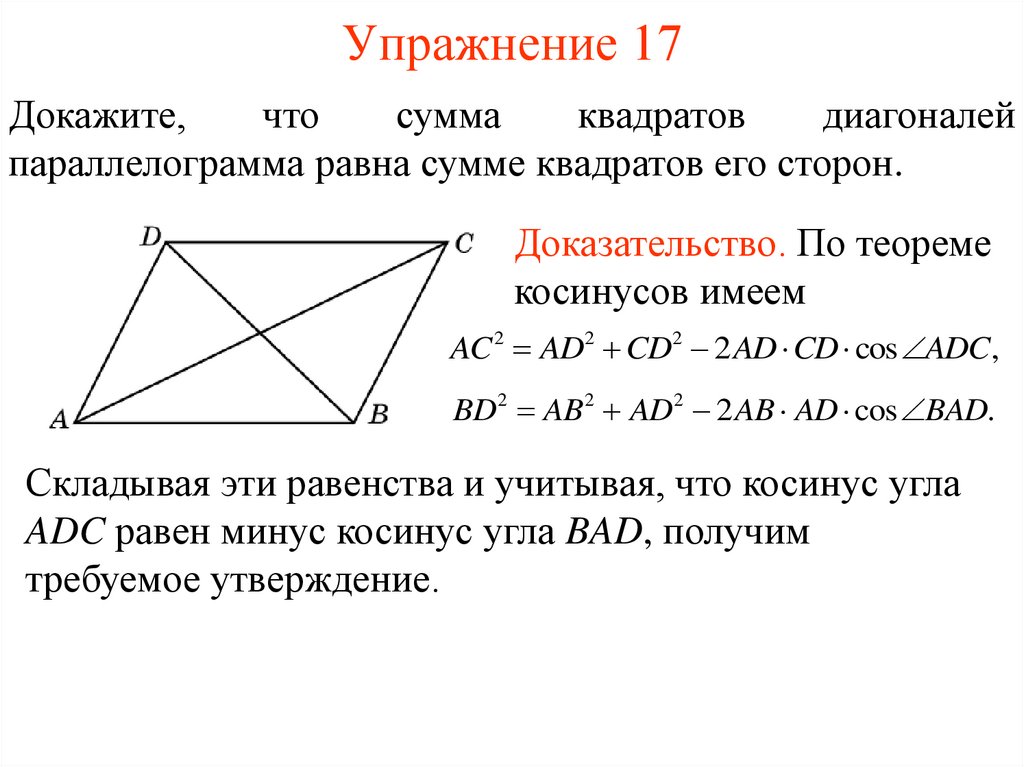
параллелограмма равна сумме квадратов его сторон.
Доказательство. По теореме
косинусов имеем
AC 2 AD2 CD2 2 AD CD cos ADC,
BD2 AB 2 AD2 2 AB AD cos BAD.
Складывая эти равенства и учитывая, что косинус угла
ADC равен минус косинус угла BAD, получим
требуемое утверждение.

3. Упражнение 18

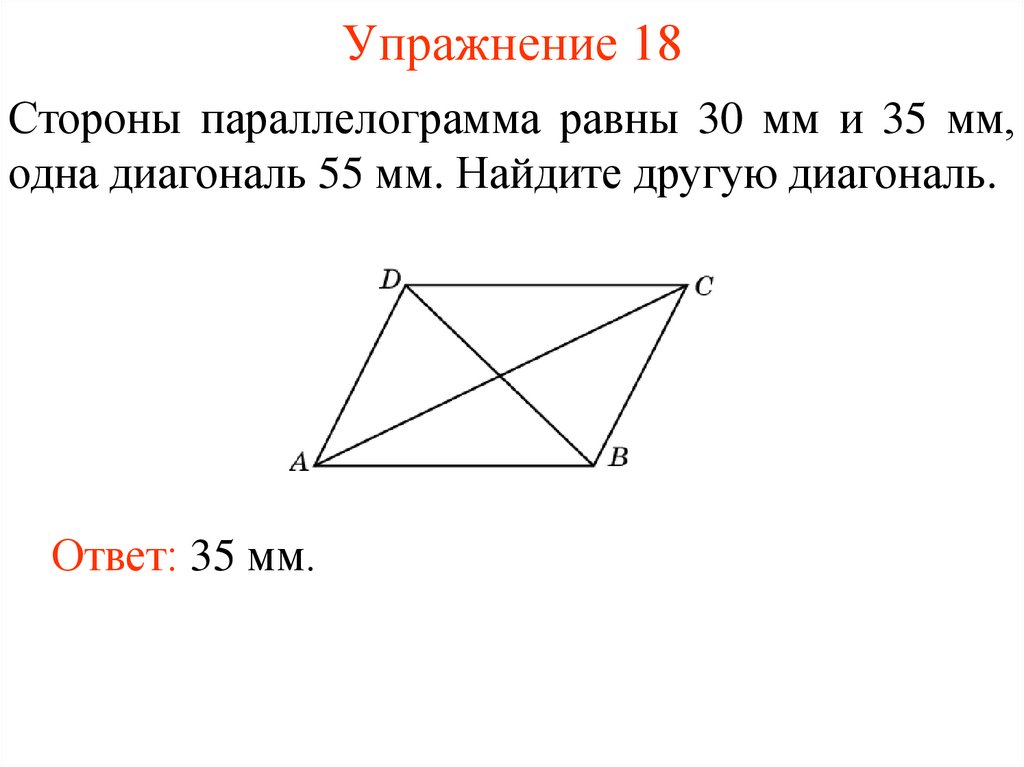
Стороны параллелограмма равны 30 мм и 35 мм,
одна диагональ 55 мм. Найдите другую диагональ.
Ответ: 35 мм.

4. Упражнение 19

Пусть в треугольнике ABC AB = c, AC = b, BC = a. Докажите, что
для медианы mc, проведенной из вершины C, имеет место формула
1
mc
2a 2 2b2 c 2 .
2
Доказательство. По теореме косинусов,
примененной к треугольникам ACD и
BCD, имеем:
2
c
c
2
2
a mc 2 mc cos BDC.
4
2
2
c
c
2
2
b mc 2 mc cos ADC ,
4
2
2
c
Складывая эти равенства, получим равенство a 2 b 2
2mc2 ,
2
из которого непосредственно следует искомая формула.

5. Упражнение 20

Стороны треугольника равны 11, 12 и 13. Найдите медиану,
проведенную к большей стороне.
Ответ. 9,5.