Декартовы координаты точек на плоскости

1.

Декартовы
координаты точек
на плоскости

2.

y
iи j
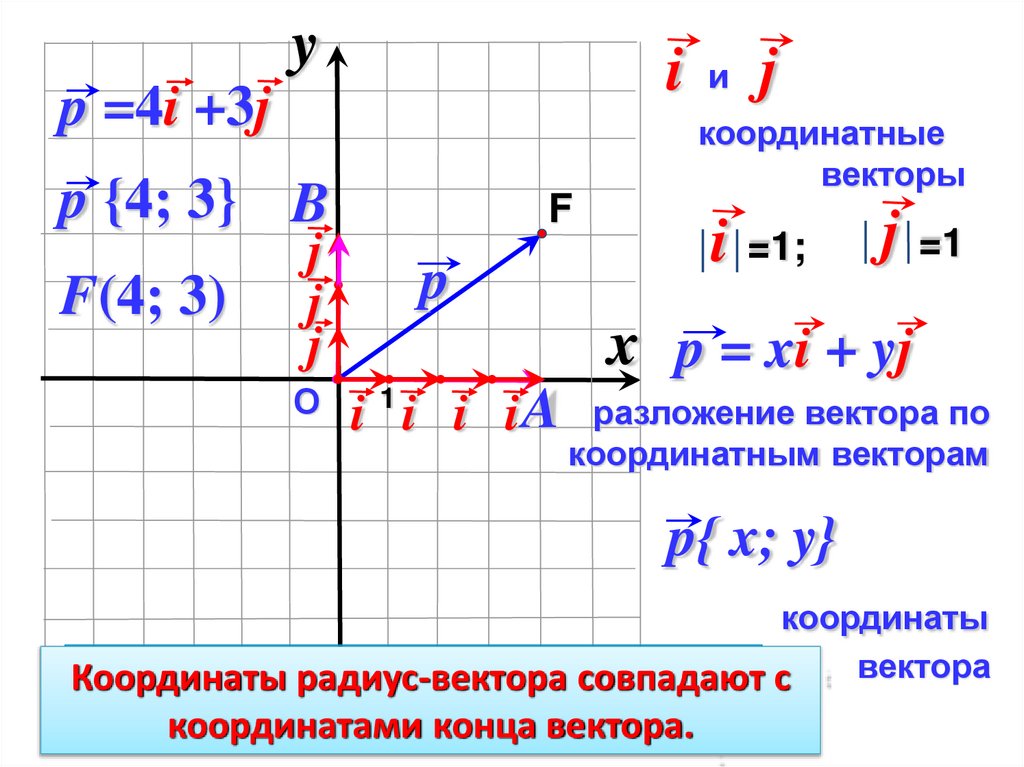
p =4i +3j
координатные
векторы
p {4; 3} B
F(4; 3)
F
j
j
j
О
p
i =1;
j =1
x p = xi + yj
1
i i i i A разложение вектора по
координатным векторам
p{ x; y}
координаты
вектора
Вектор, начало
которого совпадает
с
Координаты
радиус-вектора
совпадают
с
началом
координат –конца
радиус-вектор.
координатами
вектора.

3.

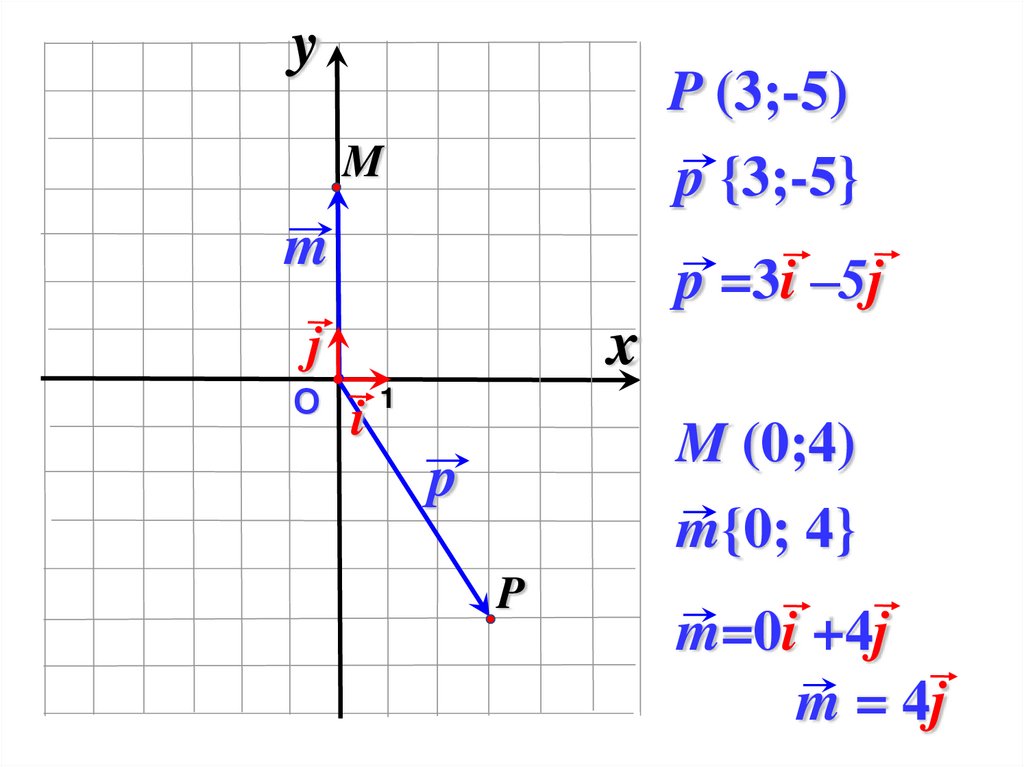
y
P (3;-5)
M
p {3;-5}
m
p =3i –5j
x
j
О
i
1
M (0;4)
p
m{0; 4}
P
m=0i +4j
m = 4j

4.

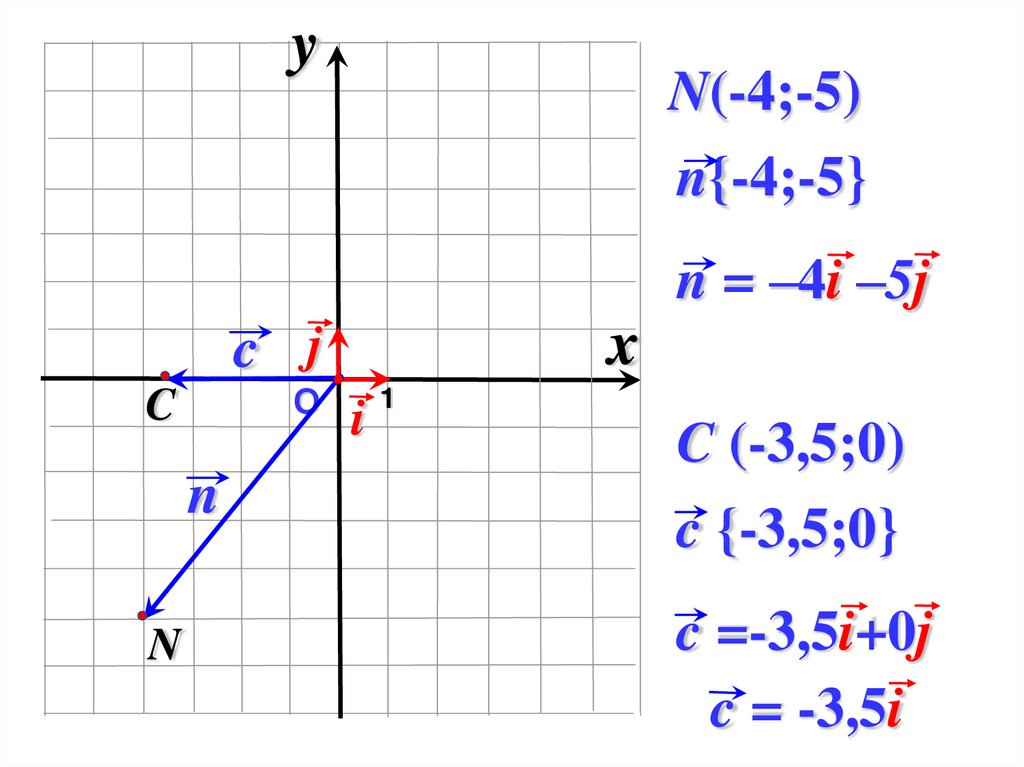
y
N(-4;-5)
n{-4;-5}
n = –4i –5j
x
c j
О
C
n
N
i
1
C (-3,5;0)
c {-3,5;0}
c =-3,5i+0j
c = -3,5i

5.

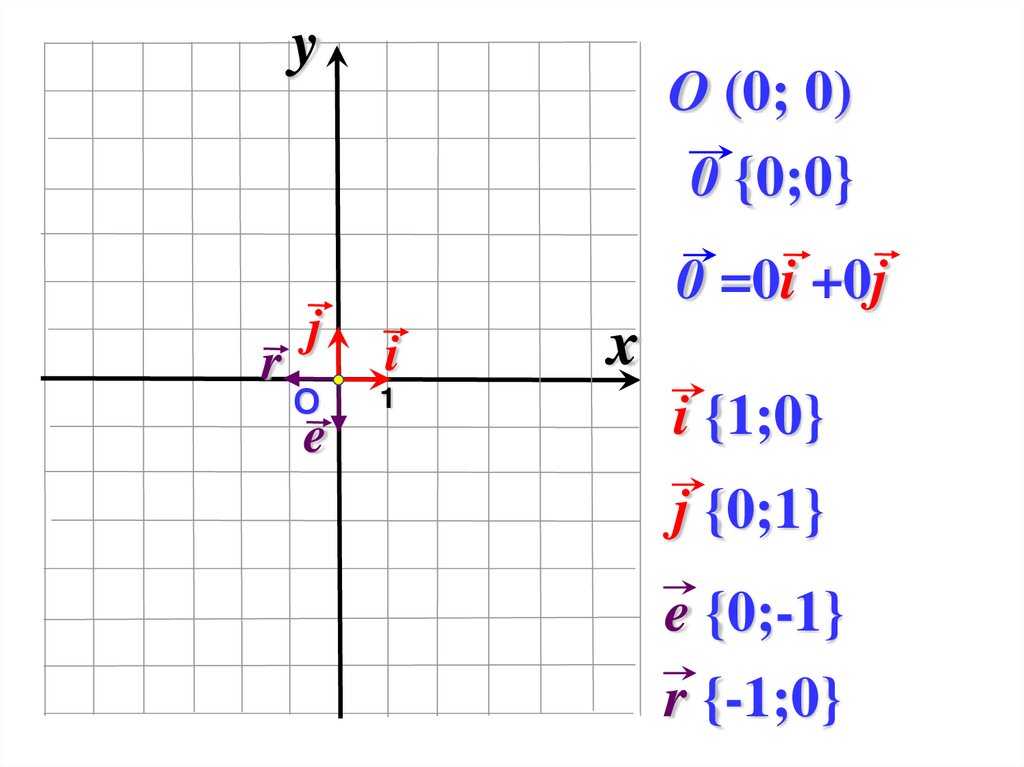
y
O (0; 0)
0 {0;0}
r
j
О
e
0 =0i +0j
i
1
x
i {1;0}
j {0;1}
e {0;-1}
r {-1;0}

6.

y
c
x
j
О
N
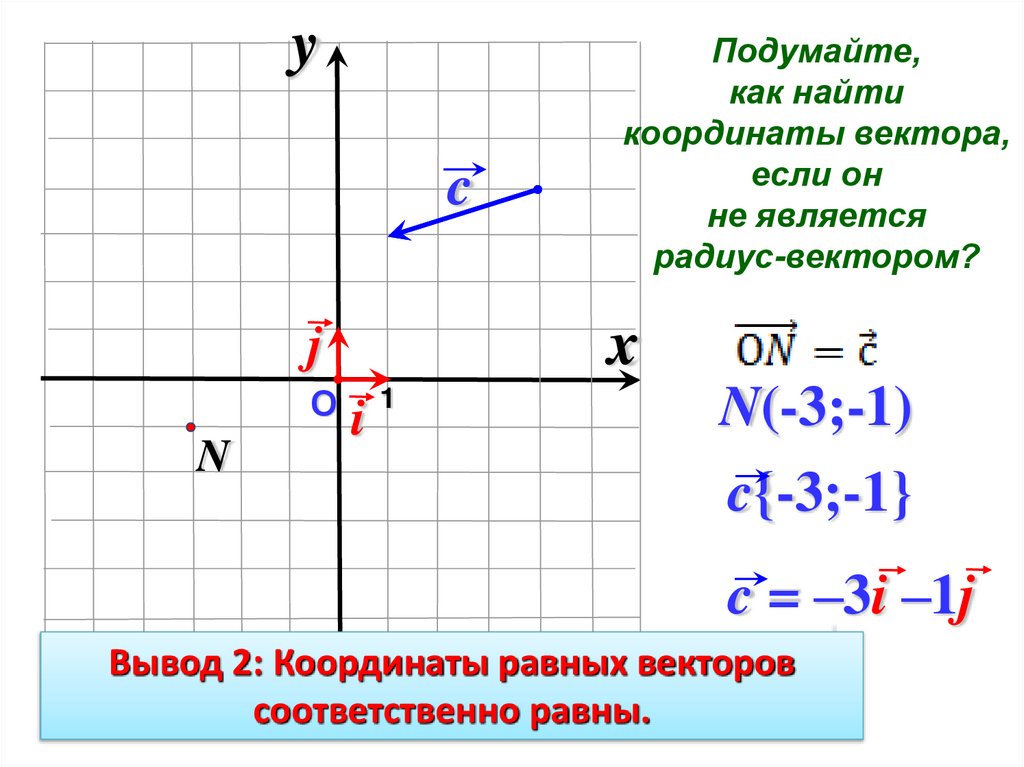
Подумайте,
как найти
координаты вектора,
если он
не является
радиус-вектором?
i
1
N(-3;-1)
c{-3;-1}
c = –3i –1j
Вывод 2: Координаты равных векторов
соответственно равны.

7.

Координаты вектора
a {-6; 9}
n {-8; 0}
c {0; -7}
m{4; -3}
? r {-5;-8}
? s {-7; 0}
? e {0; 21}
? q {0; 0}
Разложение вектора по
координатным векторам
? a = – 6i+9j
? n = – 8i+0j
? c = 0i –7j
? m =4i –3j
r = –5i –8j
s = –7i+0j
e = 0i +21j
q =0i +0j

8.

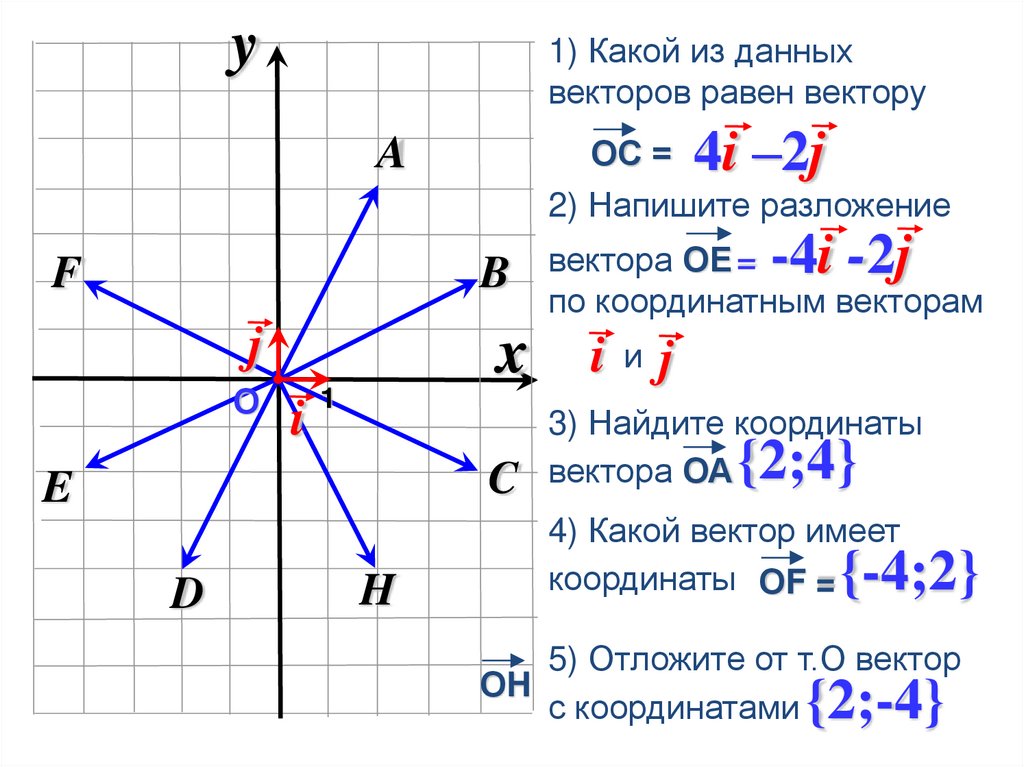
y
1) Какой из данных
векторов равен вектору
4i –2j
ОС =
2) Напишите разложение
A
F
B
j
О
x iиj
i
1
C
E
D
-4i -2j
вектора ОЕ =
по координатным векторам
H
3) Найдите координаты
вектора ОА
{2;4}
4) Какой вектор имеет
координаты ОF =
{-4;2}
5) Отложите от т.О вектор
ОH
с координатами
{2;-4}

9.

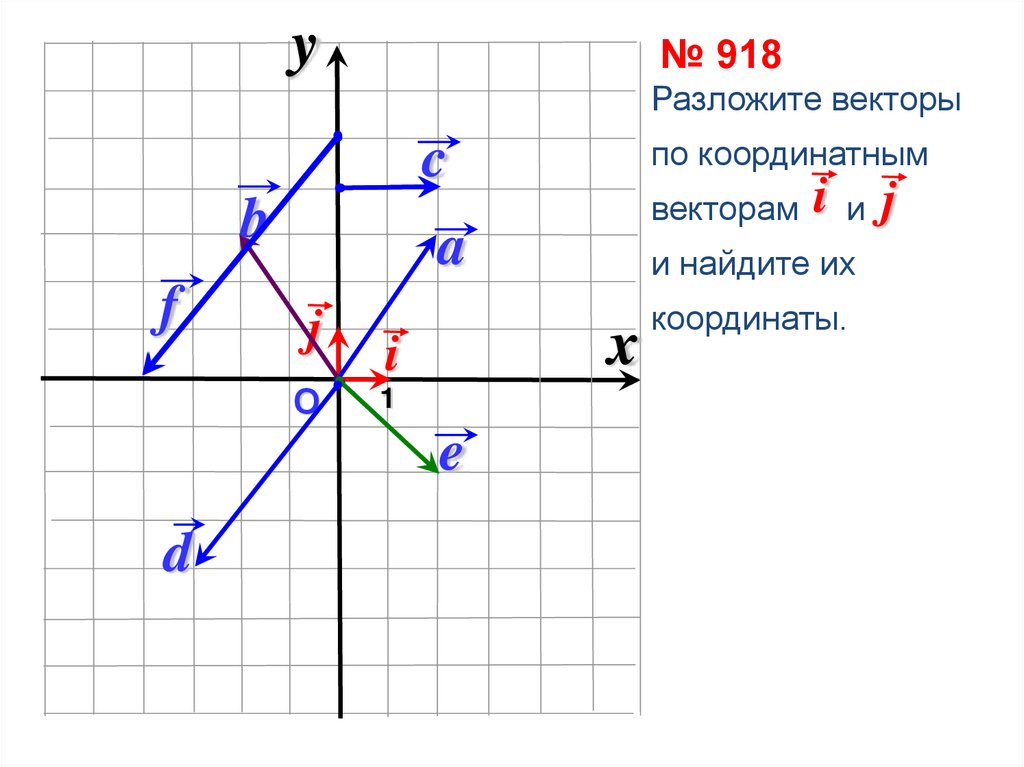
y
№ 918
Разложите векторы
b
f
j
О
c
по координатным
a
и найдите их
x
i
1
e
d
векторам i и j
координаты.

10.

y
А
Дано: ОА = ОС = 10, ОВ =6, СА Оy.
Найдите:
координаты векторов ОА, ОС, АС.
10
Решение:
8
В
6
О
x
OA{-6; 8}
10
С
OC{-6;-8}
AC{0;-16}
Теорема Пифагора:
2
2
2
a +b =c

11.

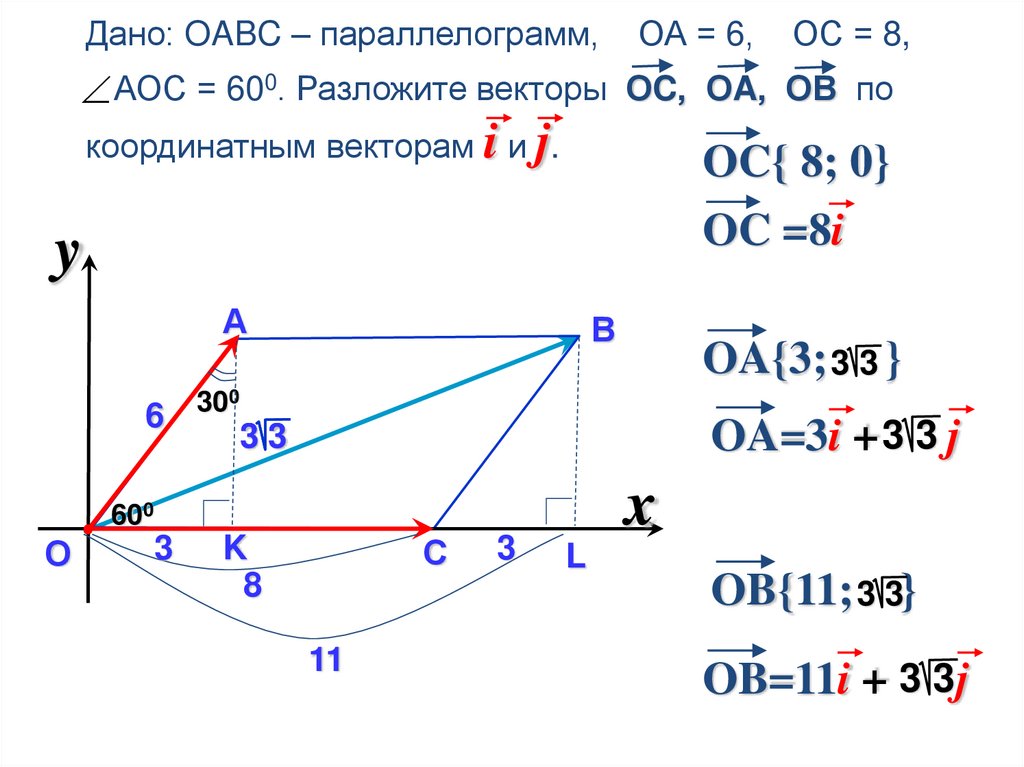
Дано: OABC – параллелограмм,
ОА = 6,
ОС = 8,
АОС = 600. Разложите векторы ОC, ОA, ОВ по
координатным векторам i и j.
OC{ 8; 0}
OC =8i
y
А
6
В
300
OA=3i + 3 3 j
33
x
600
О
3
OA{3; 3 3 }
С
K
8
11
3
L
OB{11; 3 3}
OB=11i + 3 3 j

12.

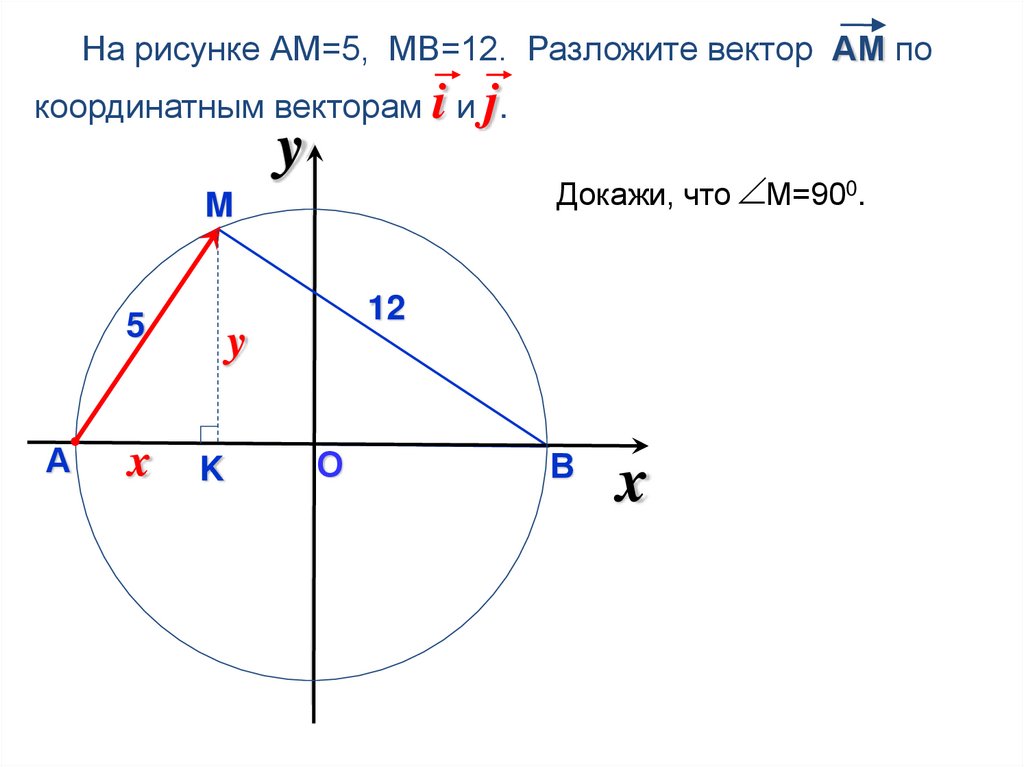
На рисунке АМ=5, МВ=12. Разложите вектор АМ по
координатным векторам i и j.
y
Докажи, что М=900.
M
5
А
x
12
y
K
О
В
x

13.

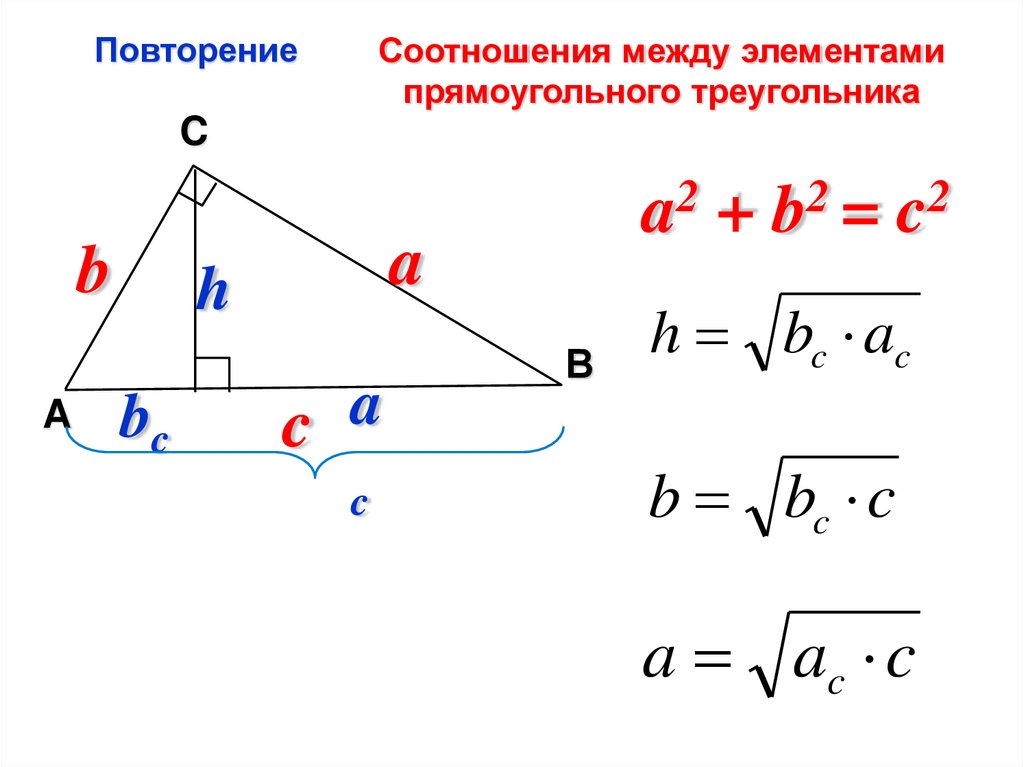
Повторение
Соотношения между элементами
прямоугольного треугольника
C
b
A
a
h
bc
a2 + b2 = c2
a
c
c
В
h bc ac
b bc c
a ac c

14.

Связь между координатами
вектора

15.

10
Каждая координата суммы двух или более
векторов равна сумме соответствующих
координат этих векторов.
Рассмотрим векторы
и
a {x1; y1}
a = x11i +y11 j
a+b =
b {x2; y2}
b+
= x2i +y2 j
=
= (x1+ x2)i + (y1 + y2 ) j
a +b {x1+x2; y1+y2}

16.

Найдите координаты вектора
a {-6; 9}
+
n {-8; 0}
a +n {-14;9}
s {-6; -4}
+
p { 2; 1}
s +p {-4;-3}
№ 922
a {3; 2}; b {2; 5}
a +b { 5; 7}
a {3;-4}; b {1; 5}
a +b { 4; 1}
a {-4;-2}; b {5; 3}
a +b { 1; 1}
a {2; 7}; b {-3;-7}
a +b {-1; 0}

17.

20
Каждая координата разности двух векторов
равна разности соответствующих координат
этих векторов.
Рассмотрим векторы
и
a {x1; y1}
b –= x22i +y22 j
a = x11i +y11 j
a–b =
(
b {x2; y2}
) =
= (x1– x2)i + (y1 – y2) j
a–b {x1–x2; y1–y2}

18.

30
Каждая координата произведения вектора на
число равна произведению соответствующей
координаты вектора на это число.
Рассмотрим вектор
a = xi +y j
a {x; y}
k
ka = kxi +ky j
ka {kx; ky}
a {-2; 1} 3
3a {-6; 3}
a {-2; 0} (-2)
-2a {4; 0}
a {-2; 5} (-1)
-a {2; -5}

19.

Найти координаты
векторов.
a {2; 4}; 3a{
}
b{-2; 0}; -2b{
}
d{-2;-3}; -3d{
}
c {2;-5}; -c{
}
e {2;-3}; 0,5e{
}
-2f{
}
f(0; 5};

20.

Найти координаты векторов.
a {2; 4}; c {3; 2}; a +c {
}
b{-2; 0}; d{-2;-3};
b+d{
}
c {2;-5}; e {2;-3};
c +e{
}
f(0; 5}; d{-2;-3};
f - d{
}
b{-2; 0}; d{-2;-3};
b - d{
}
a {2; 4}; c {3; 2};
a - c{
}

21.

a-b
b {-8;12}
Найдите координаты вектора
a {-6; 9}
1 способ
2 способ
a {-6; 9}
a {-6; 9}
-
+
b {-8;12}
-b{8;-12}
a - b {2;-3}
a - b {2;-3}

22.

Даны векторы
a{2;-4} b{-5;. 3}
Найдите координаты векторов
m = 4a-2b n = 3a-4b
4a{8;-16}
4
+
-2b{10;-6}
(-2)
4a-2b
m{18;-22}
{18;-22}
Разложите полученные векторы по
координатным векторам i и j.
3
(-4)
3a{6;-12}
+
-4b{20;-12}
3a-4bn{26;-24}
{26;-24}

23.

№929 Точка А лежит на положительной полуоси Ох,
а точка В – на положительной полуоси ОУ. Найдите
координаты вершин треугольника АВО, если
y
B (0; b3))
а) ОА = 5, ОВ = 3;
б) ОА = a, ОВ = b
b3
x
O (0; 0) 5a
A ((5;
a; 0)
0)

24.

a{-4; 8}; b{-3;-2};
Найти координаты векторов.
a + b {-7; 6}
a – b {-1;10}
-a {4;-8}
2a {-8;16}
-3b { 9; 6}
2a – 3b { 1; 22}

25.

Простейшие задачи в
координатаха

26.

Выразим
координаты
вектора
АВ через
координаты
его
Каждая
координата
вектора
равна
разности
начала А и конца В.
соответствующих координат его конца и начала.
из ОАВ
y
AB = AO + OВ = – OA + OВ
OA{x1;y1} (-1)
B (x2;y2)
+
–OA{-x1;-y1}
OB{ x2; y2}
A(x1;y1)
O
x
– OA + OВ {x2 - x1; y2 - y1}
AB {x2 - x1; y2 - y1}

27.

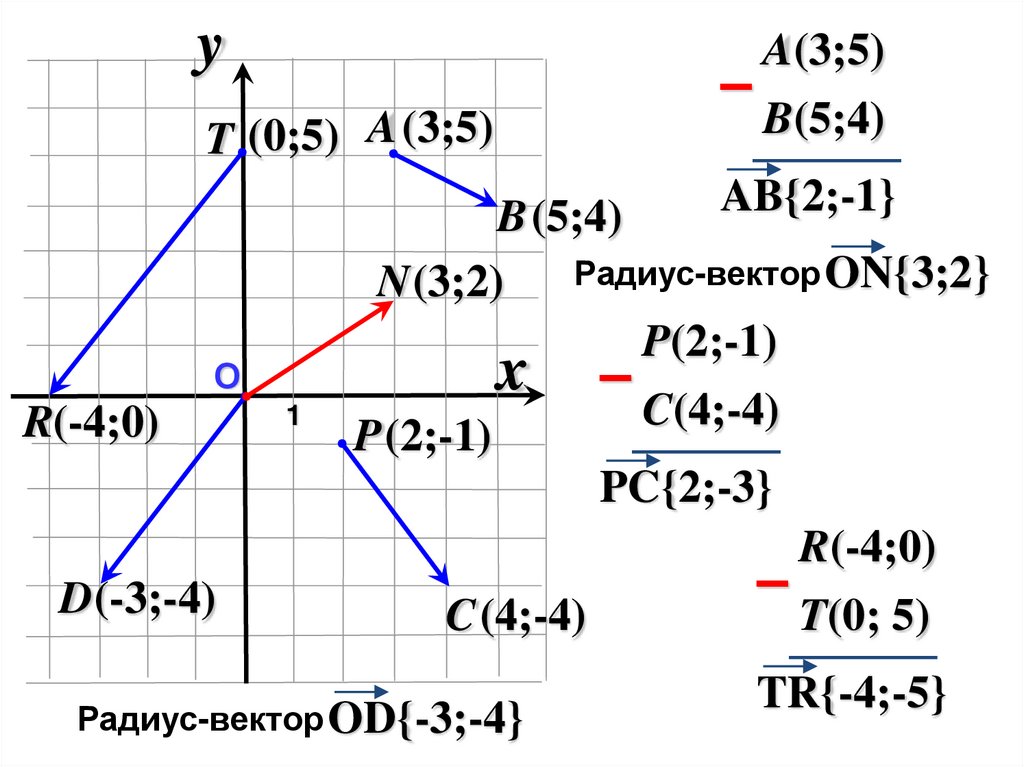
y
T (0;5) A(3;5)
О
R(-4;0)
D(-3;-4)
1
A(3;5)
–
B(5;4)
AB{2;-1}
B (5;4)
Радиус-вектор ON{3;2}
N(3;2)
P(2;-1)
x –
C(4;-4)
P (2;-1)
PC{2;-3}
R(-4;0)
–
C (4;-4)
T(0; 5)
Радиус-вектор OD{-3;-4}
TR{-4;-5}

28.

Найдите координаты
векторов
M(-2;7)
–
R(2;7); M(-2;7); RM
R(2; 7)
RM{-4; 0}
P(-5;1); D(-5;7); PD
D(-5;7)
– P(-5; 1)
PD{ 0; 6}
N(0; 5)
– R(-3;0)
RN{3; 5}
A(0; 3)
– B(-4;0)
BA{4; 3}
B(-2;0)
– A(-2;7)
AB{0;-7}
T(-2;-7)
– R(-7; 7)
RT{5;-14}
R(-3;0); N(0;5);
RN
A(0;3); B(-4;0);
BA
A(-2;7); B(-2;0); AB
R(-7;7); T(-2;-7); RT

29.

Обратные задачи.
Дано:AB{2;-1}, B(5;4)
Дано:AB{2;-1}, A(2;-4)
Найти: A(x;y)
Найти: B(x;y)
B(5; 4)
–
A(x; y)
B(x; y)
–
A(2;-4)
AB{2;-1}
AB{2;-1}
5–x=2
4 – y = -1
x–2=2
y + 4= -1
x=3
y=5
x=4
y = -5

30.

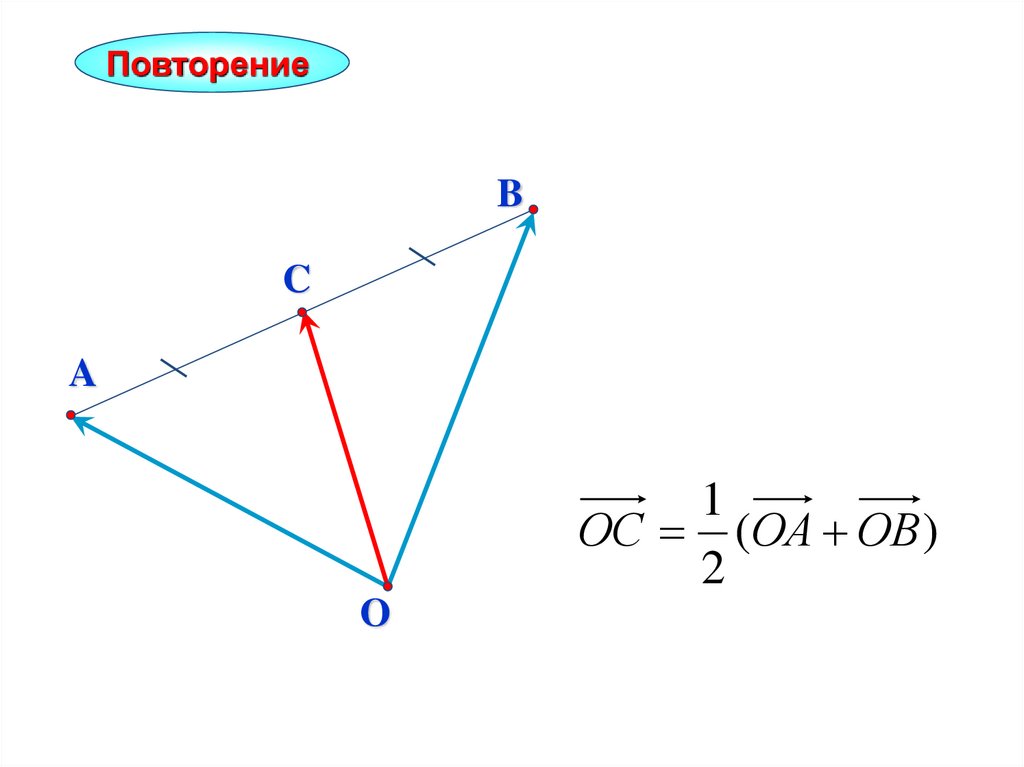
Повторение
B
C
A
1
ОС (ОА ОВ )
2
O

31.

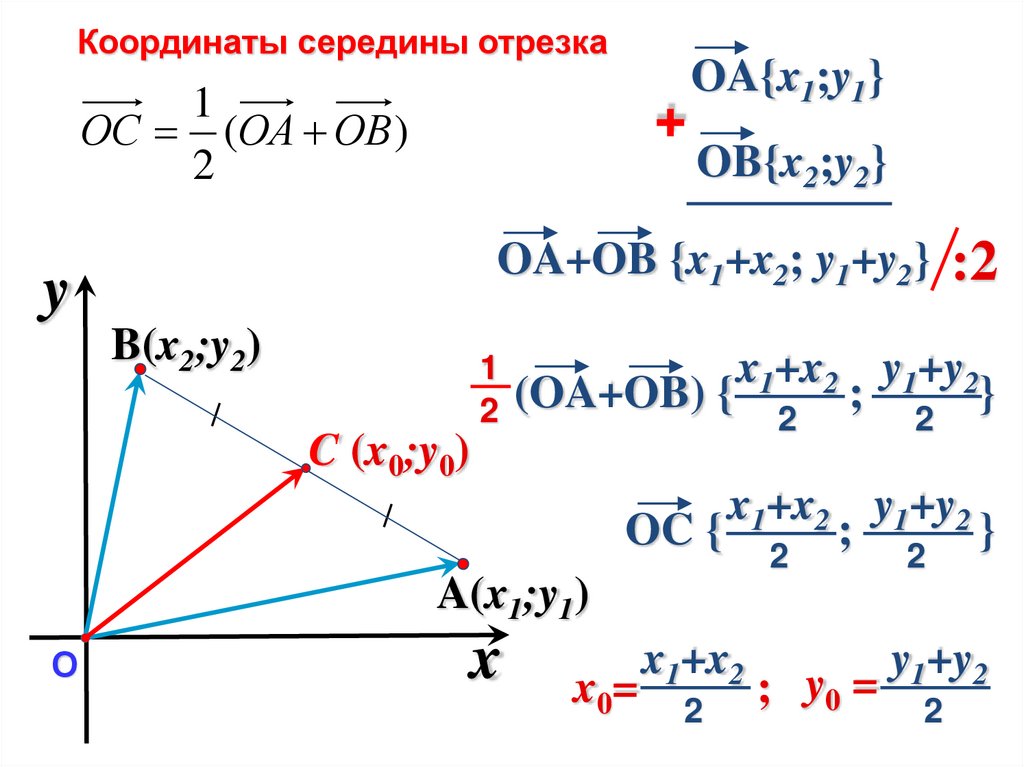
Координаты середины отрезка
1
ОС (ОА ОВ )
2
+
OA{x1;y1}
OB{x2;y2}
OA+OB {x1+x2; y1+y2} :2
y
B(x2;y2)
C (x0;y0)
1
x1+x2 y1+y2
;
}
2 (OA+OB) { 2
2
x1+x2 y1+y2
OC {
;
}
2
2
A(x1;y1)
О
x
x0=
x1+x2
2
; y0 =
y1+y2
2

32.

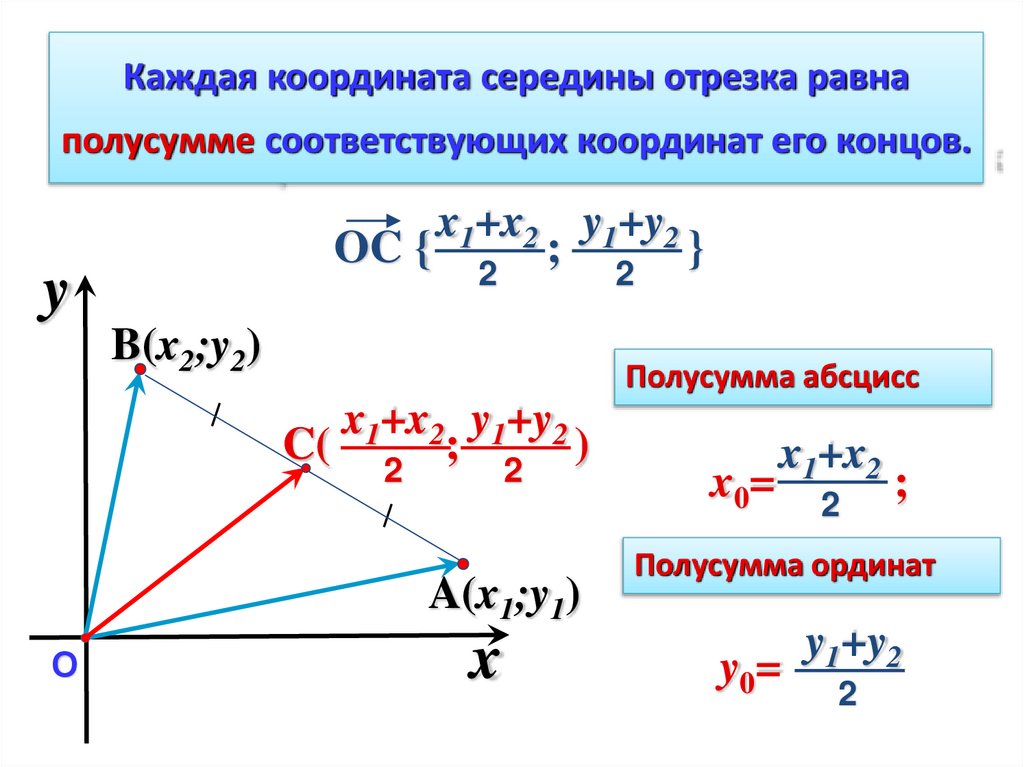
Каждая координата середины отрезка равна
полусумме соответствующих координат его концов.
x1+x2 y1+y2
OC {
;
}
2
y
2
B(x2;y2)
Полусумма абсцисс
x1+x2 y1+y2
C(
C
;
)
2
2
A(x1;y1)
О
x
x0=
x1+x2
2
;
Полусумма ординат
y0=
y1+y2
2

33.

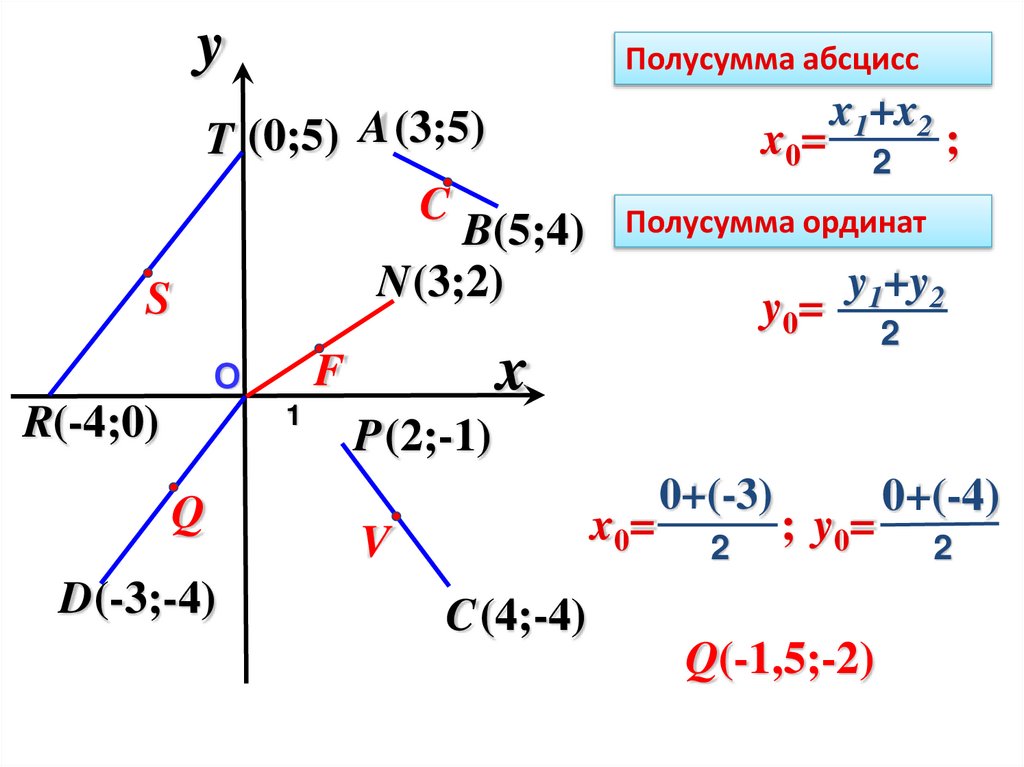
y
Полусумма абсцисс
T (0;5) A(3;5)
x0=
C
B(5;4)
N(3;2)
S
1
R(-4;0)
Q
D(-3;-4)
2
P (2;-1)
V
C (4;-4)
;
Полусумма ординат
y0=
y1+y2
x
F
О
x1+x2
2
323 +0
+5
2-1+(-4)
5 +0
+4
+4
0+(-4)
5+0;;
xxx00=
=
;
;
y
y
=
=
0+(-3)
0+(-4)
0
0
=
;
y
=
xx000== 22222 ;; 0yy00==22 222
C(4;
4,5)
F(1,5;
1)
V(3;-2,5)
Q(-1,5;-2)
S(-2;2,5)

34.

Обратная задача.
Дано: A(5; 4); C(-3; 2) – середина отрезка AB
Найти: B(x; y)
x 0=
-3=
x1+x2
2
5+x
2
;
; 2
A(5; 4)
C(-3; 2)
y0=
2=
B(x; y)
y1+y2
2
4+y
2
–6=5+x
4=4+y
x = – 11
y=0
;
2
B(-11; 0)

35.

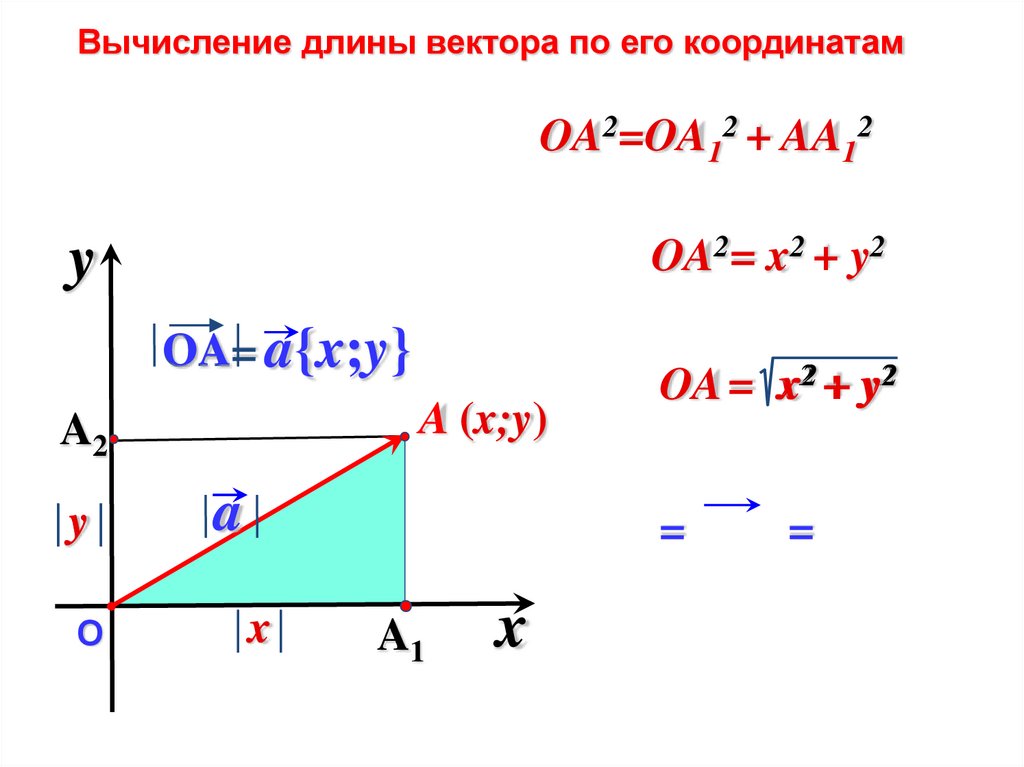
Вычисление длины вектора по его координатам
OA2=OA12 + AA12
y
OA2= x2 + y2
OA
OA= a{x;y}
A (x;y)
A2
y
О
a
OA = x2 + y2
=
x
A1
x
=

36.

Расстояние между двумя точками
y
M2(x2;y2)
–
d
M2(x2;y2)
M1(x1;y1)
M1M2 {x2–x1; y2–y1}
M1(x1;y1)
O
x
a = x2 + y2
M1M2 = (x2–x1)2+(y2–y1)2
d = (x2–x1)2+(y2–y1)2

37.

№ 940
Найдите расстояние между точками
A(2;7) и B(-2;7)
1)
1 способ
2 способ
a =
M1M2 = (x2–x1)2+(y2–y1)2
x2 + y 2
B(-2; 7)
–
A( 2; 7)
AB = (–2–2)2+(7– 7)2
AB{-4; 0}
2)
AB = (-4)2 + 02 = 16 = 4

38.

ABCО – прямоугольная трапеция. Найдите
координаты точек A, B, C, O, N и P, где N и P –
середины диагоналей OB и AC соответственно.
N(1,5; 1,5); P(1,5; 2,5)
y
Найдите координаты векторов
C (0;5)
5
P
N
O
3
B (3;3)
OB {3; 3}
CA {3;-5}
AB {0; 3}
NP {0; 1}
Найдите
3
A(3;0)
x
CA = 32 + (-5)2
NP = 02 + 12

39.

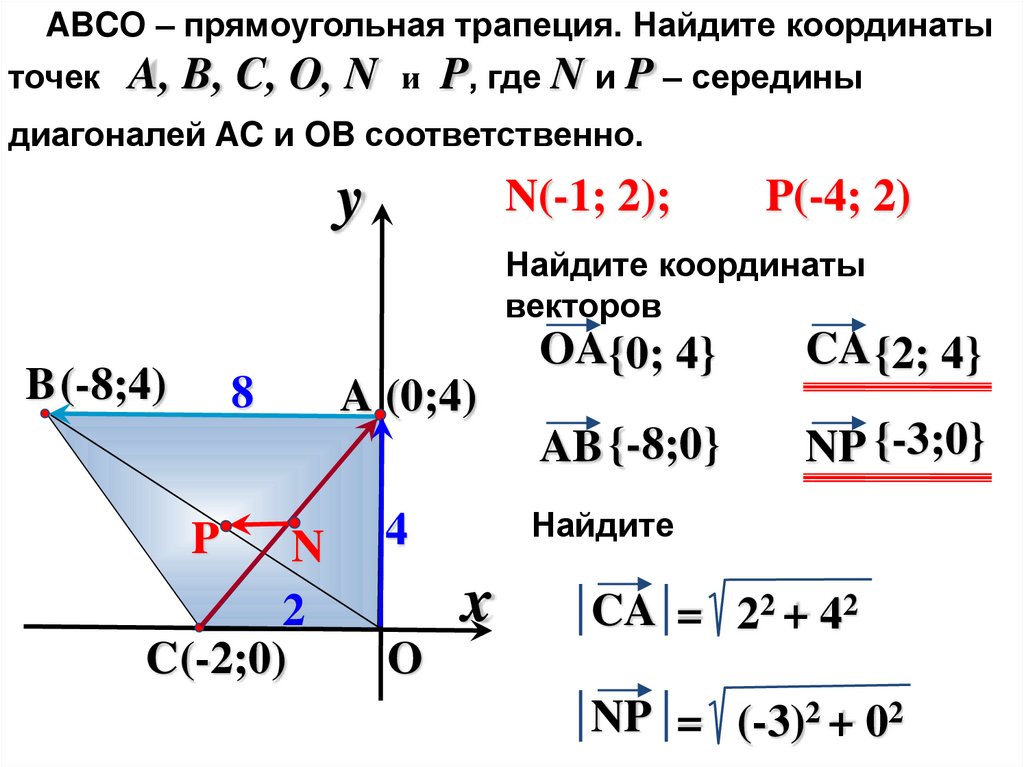
ABCО – прямоугольная трапеция. Найдите координаты
точек
A, B, C, O, N и P, где N и P – середины
диагоналей AC и OB соответственно.
y
N(-1; 2);
P(-4; 2)
Найдите координаты
векторов
B (-8;4)
8
P
N
2
C(-2;0)
OA{0; 4}
CA {2; 4}
AB {-8;0}
NP {-3;0}
A (0;4)
Найдите
4
x
CA = 22 + 42
O
NP = (-3)2 + 02