Дискретная математика

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «Программное обеспечение»
Курс «Дискретная математика»
ВВЕДЕНИЕ
Автор Макарова О.Л.
Ижевск
2013

2.

Немного истории
Ситуация 1 ( парадокс Рассела )
Одному
деревенскому
брадобрею
приказали «брить всякого, кто не
бреется сам, и не брить того, кто
сам бреется».
Кто должен брить брадобрея?
Курс «Дискретная математика»
Введение
2

3.

Немного истории
Ситуация 2 ( задача о Кенигсбергских мостах )
На рисунке представлен план
центральной части города
Кенигсберг, включающий два
берега реки Перголя, два
острова и соединяющие их
мосты. Во время прогулки в 1736г. математик Л.Эйлер
задался вопросом, можно ли пройти по всем семи
мостам, побывав на каждом только один раз, причем
начало и конец пути должны совпадать?
Курс «Дискретная математика»
Введение
3

4.

Немного истории
Ситуация 3 ( задача о красках )
В середине XIX века в одной из
британских
картографических
типографий резонно возник вопрос:
«Сколько красок достаточно для
правильного раскрашивания всех
графств на карте Англии»(любые две
области, имеющие общий участок
границы, должны быть раскрашены в
разные цвета)?
Курс «Дискретная математика»
Введение
4

5.

Немного истории
Проблема:
Недостаток математического
аппарата
Решение:
Создание нового
математического стандарта
Курс «Дискретная математика»
Введение
5

6.

Немного истории
Конец XIX века Георг Кантор создал
современную теорию множеств
Начало XX века бурное развитие
дискретной (компьютерной)
математики
Курс «Дискретная математика»
Введение
6

7.

Немного истории
Ситуация 4 ( задача современности )
Несколько лет назад было предложено
объединить ИжГТУ и УдГУ
в единое образовательное пространство.
1. Предложите вариант алгоритма для объединения
списков сотрудников и преподавателей обоих ВУЗов
(пусть в ИжГТУ и УдГУ работает по 1500 человек).
Следует учесть, что есть преподаватели, работающие в
обоих ВУЗах параллельно.
2. Подсчитайте число операций вашего алгоритма.
Курс «Дискретная математика»
Введение
7

8.

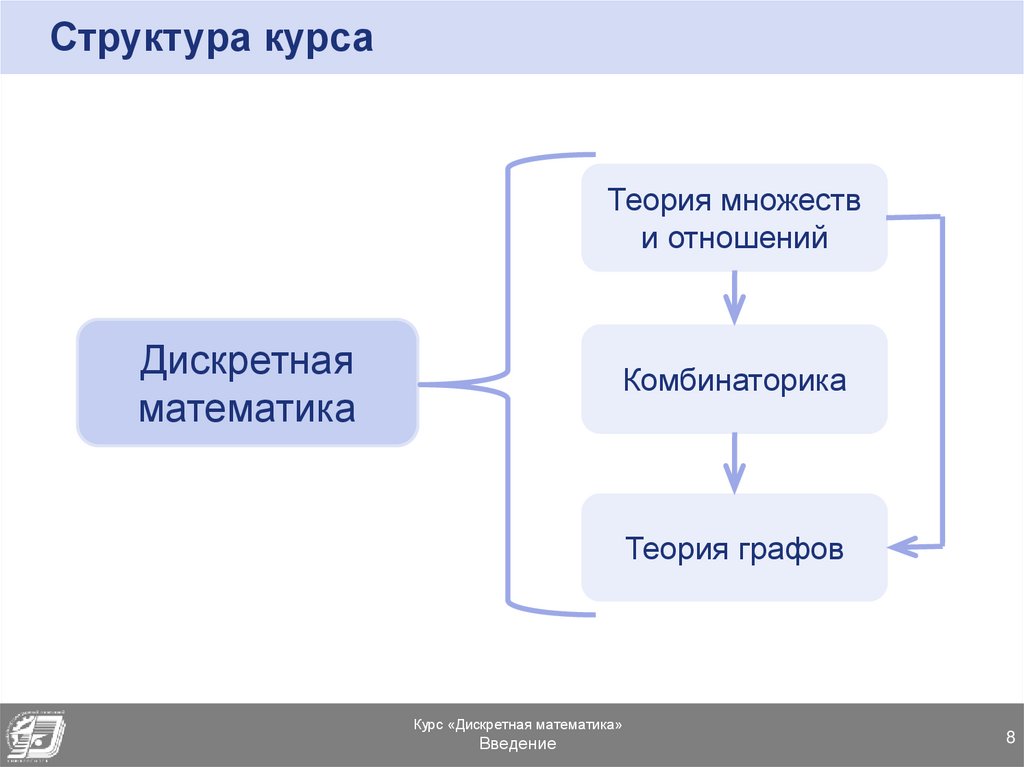
Структура курса
Теория множеств
и отношений
Дискретная
математика
Комбинаторика
Теория графов
Курс «Дискретная математика»
Введение
8

9.

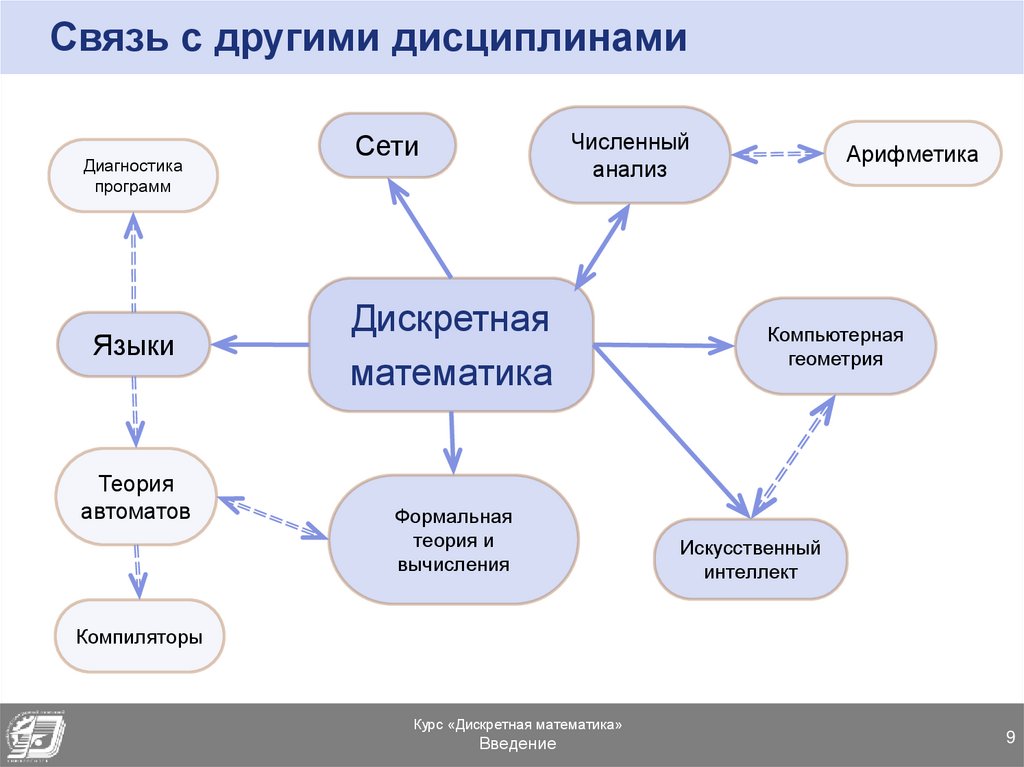
Связь с другими дисциплинами
Диагностика
программ
Языки
Теория
автоматов
Численный
анализ
Сети
Дискретная
математика
Формальная
теория и
вычисления
Арифметика
Компьютерная
геометрия
Искусственный
интеллект
Компиляторы
Курс «Дискретная математика»
Введение
9

10.

Цели и задачи курса
Цели курса:
• получение базовых знаний в области дискретной математики;
• выработка умения самостоятельно решать задачи дискретного
анализа;
• овладение навыками использования методов дискретного
анализа при решении различного класса задач
По окончании курса вы сможете:
решать типовые задачи дискретной математики;
описывать данные математическими методами;
представлять математические объекты в программах;
использовать основные алгоритмы решения типовых задач
дискретной математики на практике
Курс «Дискретная математика»
Введение
10

11.

СИСТЕМА ОЦЕНИВАНИЯ
Что оценивается?
1. Лекции
2. Практические работы
3. Лабораторные работы
4. Участие в учебных форумах
Максимальное количество баллов - 120
«Отлично»: 108 - 120
«Хорошо»: 90 - 107
«Удовлетворительно»: 79 – 89
Курс «Дискретная математика»
Введение
11

12.

ВАШ ПРЕПОДАВАТЕЛЬ
Макарова Ольга Леонидовна,
ведущий инженер-программист,
старший преподаватель
кафедры «Программное обеспечение»
ФГБОУ ВПО
«ИжГТУ имени М.Т. Калашникова»
Контакты:
email: ol@istu.ru
раб.т. (3412)58-38-74
Курс «Дискретная математика»
Введение
12

13.

English Русский Правила