Похожие презентации:
Возможности и использование системы компьютерной математики MathCad
1. Тема 14. Возможности и использование системы компьютерной математики MathCad
12.
СПИСОК ЛИТЕРАТУРЫ1. Дьяконов В. Mathcad 2000: учебный курс.- СПб.: Питер,
2001
2. Охорзин В.А. Компьютерное моделирование в системе
MathCad. Учебный курс. –М.: Финансы и статистика, 2006
Методические указания
1. Методические указания к выполнению контрольных работ по
теме «Решение задач в среде MathCad», №3394.
3. Основные приемы работы в системе MathCAD.
прикладных технических задач, № 2601.
Решение
4. Задания к лабораторным работам по теме «Математический
пакет Mathcad», №2774.
3. Решение систем алгебраических и дифференциальных
2
уравнений в среде MathCAD Windows, №2453.
3.
1. Основные функции системыНаиболее
известными
математики (СКМ) являются:
системами
компьютерной
• Mathematica
• Maple
численные и
аналитические вычисления
• Matlab
• MathCAD
в основном численные
вычисления
Система Mathcad используется для инженерных и простейших научных
расчетов. Характерной ее особенностью является использование
стандартных математических обозначений, удобный математикоориентированный интерфейс, доступность разнообразных численных
методов.
Пакет ориентирован в первую очередь на проведение численных
расчетов, но имеет встроенный символьный процессор Maple, что позволяет
выполнять аналитические преобразования. Mathcad
является средой
визуального программирования, то есть не требует знания специфического
3
набора команд.
4.
Все функции системы можно классифицировать следующимобразом:
вычислительные
графические
программные
сервисные
аналитические
4
5.
К основным вычислительным функциям относятся:• вычисление
точностью
арифметических
выражений
с
различной
• использование встроенных математических функций и
создание пользовательских функций
• вычисление производных, интегралов, сумм и произведений
• обработка матриц, векторов и дискретных переменных
• выполнение
переменными
операций
с
размерными
величинами
и
• решение уравнений, неравенств и их систем
• решение
дифференциальных
дифференциальных уравнений
уравнений
и
систем
• использование символьных преобразований и вычислений
5
6.
Графические возможности системы применяются длявизуализации результатов вычислений и включают
построение:
• двумерных графиков и графиков поверхностей
• карт линий уровня
• трехмерных диаграмм
• точечных графиков и графиков векторных полей
6
7.
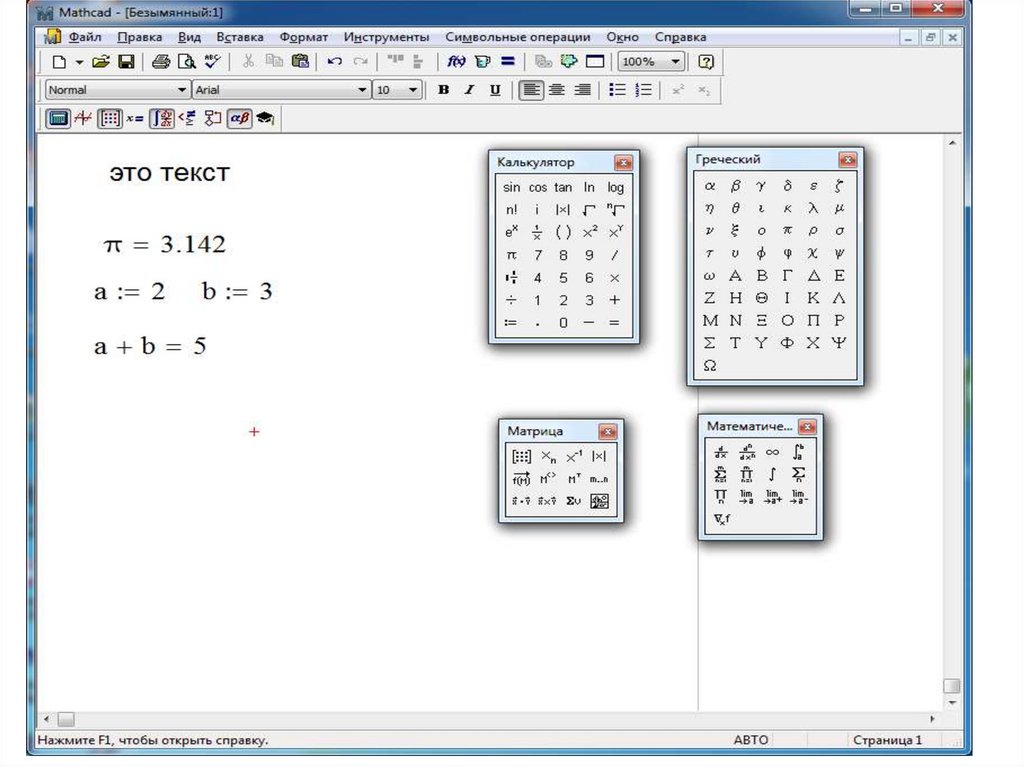
2. Интерфейс системыОкно системы содержит следующие элементы:
строка заголовка
строка управляющего меню: Файл – Правка - ....
панели инструментов Стандартная и Форматирование
панель
инструментов
Математика,
содержащую
пиктограммы палитр шаблонов математических символов (ПИ)
для удобного набора документа в MathCAD
окно набора и редактирования документа (основная часть
экрана, предназначенная для обработки документа MathCAD)
строка состояния (Auto или CalcF9)
Все ПИ можно вывести на экран и убрать с него с помощью
меню Вид.
7
8.
89.
Основную частьредактирования.
экрана
занимает
окно
набора
и
Одновременно можно работать в системе с несколькими
документами в разных окнах набора и редактирования.
Перемещение между ними выполняется с помощью меню
Окно.
Создание нового документа выполняется с помощью
команды
Файл – Создать – Пустой документ
или инструмента Создать
9
10.
3. Работа с документомДокумент системы MathCAD строится из областей, которые делятся на
вычислительные, графические, текстовые. MathCad создает невидимый
прямоугольник, содержащий каждую область. Области обрабатываются
тремя различными процессорами и создаются, соответственно, средствами
формульного, графического и текстового редакторов.
Общение пользователя с системой происходит на промежуточном
математически ориентированном языке визуального программирования.
Подготовка вычислительных блоков облегчается благодаря вводу шаблонов.
Для этого служат панели (палитры) с набором шаблонов различных
математических символов.
По мере того, как пользователь создает различные типы объектов –
выражения, формулы, тексты, графики, система сама составляет программу,
которая хранится в памяти компьютера и сохраняется на диске в виде
файла с расширением mcd или xmcd. Именно эта программа
обрабатывается системой для получения результатов вычислений.
10
11.
При создании и редактировании объектов разных типов(выражений, графиков, текстов) используются курсоры
разного вида:
курсор в виде маленького красного крестика (визир), определяющий
начало формирования новой области на свободном поле документа
курсор в виде синей вертикальной линии, используемый внутри
формульной или графической области при наборе и редактировании
курсор в виде тонкой красной вертикальной линии, используемый
внутри текстовой области при наборе и редактировании
курсор в виде рамки (перекрестья) синего цвета (рамка объекта),
заключающей внутри себя часть или все выражение.
Часть выражения, содержащаяся в рамке объекта, становится первым
(вторым, если нажать клавишу Insert) операндом следующего оператора,
для увеличения или уменьшения рамки используются клавиши управления
курсором (← →), клавиша пробел (для увеличения) или щелчок мышью
курсор в виде раскрытой ладони, применяемый для копирования и
11
перемещения выделенных объектов
12.
Операции с областями• выделение областей (одной – щелчком мышью, нескольких –
обвести вокруг них мышью пунктирную рамку)
• разделение областей (выделенных)
Формат – Разделение областей (регионов)
• удаление областей
Правка – Удалить
Выделить содержимое области цветом или обвести рамкой,
нажать Delete
• выравнивание областей по вертикали и горизонтали
Формат – Выравнивание областей… или кнопки на ПИ
• копирование и перемещение областей
• использование буфера обмена
12
• перетаскивание мышью (для копирования удерживать Сtrl)
13.
Текстовая область создается с помощью командыВставка – Область (регион) текста
или нажатием клавиши " (двойные кавычки).
На поле документа появляется черная текстовая рамка и
текстовый курсор, с помощью которого можно вводить и
редактировать текстовую информацию.
Длина текстовой области ограничена длиной наибольшей
строки, каждая из которых заканчивается нажатием клавиши
Enter.
13
14.
В процессе работы с документом используетсяавтоматический (по умолчанию) и ручной режим
вычислений. В автоматическом режиме вычисляются все
видимые на экране области документа.
При просмотре документа вновь появившиеся области
вычисляются автоматически, что не всегда удобно при
выполнении больших расчетов.
В ручном режиме вычисления производятся с помощью
команды Инструменты – Вычислить , кнопки со знаком =
на ПИ или клавиши F9.
Для перехода в ручной режим необходимо выключить
режим Автовычисление (убрать флажок) в меню
Инструменты.
14
15.
Типы данных. Входной язык системыВходной язык системы
интерпретирующего типа.
MathCAD
–
это
язык
Как только система распознает объект, автоматически
запускается внутренняя подпрограмма, выполняющая
необходимые
действия.
Например,
вычисление
выражения, вывод таблицы и т.д.
Документ обрабатывается сверху вниз, а в пределах
строки слева направо. Поэтому все переменные,
используемые в вычислительных или графических
областях, должны быть определены в документе в строках
выше или слева в той же строке.
15
16.
Алфавит входного языка системы включает• строчные и прописные буквы латинского и греческого
алфавитов
• арабские цифры от 0 до 9
• системные переменные
• операторы
• имена встроенных функций
• специальные знаки
Основные элементы языка системы
константы
переменные
операции и операторы
функции
управляющие структуры
16
17.
Переменные могут быть простыми и структурированными.К структурированным относятся дискретные переменные,
массивы и файлы.
В MathCAD тип переменной определяется значением и
предварительно не задается. Переменные могут быть
числовыми и строковыми. Имена констант и переменных
состоят из латинских и греческих букв и цифр, начинаться
идентификатор может только с буквы.
Строчные и прописные буквы в идентификаторах
различаются.
Константы могут быть
• целые ( 384 )
• вещественные ( 1.2 )
• комплексные ( 5+2.3i )
• зарезервированные ( e, π, % )
• строковые ( "пример" )
17
18.
В MathCAD содержится группа системных переменных,имеющих определенное значение. Изменение значений этих
переменных для открытого документа можно выполнить с
помощью команды
Инструменты – Параметры документа
или установить в пределах своего документа как и любых
других переменных.
TOL – определяет погрешность численных методов при
расчетах, значение по умолчанию 0.001
ORIGIN – определяет начальное значение номера элемента,
строки или столбца в массиве, по умолчанию 0
Обычные переменные отличаются от системных тем, что их
значения должны быть определены перед их использованием в
выражениях.
18
19.
К базовым операторам системы относятся: = – оператор локального присваивания
= – оператор вычисления
– оператор глобального присваивания
Локальное присваивание (:=) распространяет свое
действие на область документа, расположенную ниже места
присваивания и справа в той же строке.
Если значение переменной в выражении не определено,
переменная выделяется цветом.
a : =2 c : = a + b
b:=3
19
20.
Глобальное присваивание ( ) не зависит от местарасположения и распространяет свое действие на весь
документ.
a : =2 c : = a + b
b≡3
Можно изменить вид результата вычислений выделенного
выражения с помощью команды Формат – Результат…,
указав, например, число выводимых десятичных разрядов на
вкладке числовых форматов.
Форматирование переменных или констант
одновременно) можно выполнить с помощью команды
(всех
Формат – Уравнение…
или с помощью ПИ, предварительно выделив любую
20
переменную или константу.
21.
Вычисление значений выраженийВыражение может содержать
константы, переменные,
заполненные
математические
шаблоны,
возвращающие
значения, функции, знаки арифметических операций. При
записи выражения можно использовать ПИ Калькулятор.
Вычисление значений выражений:
1 способ:
выражение =
Пример:
2 3
sin 0.4 1.75
13.61
2.3
e
21
22.
2 способ:имя_переменной := выражение
имя_переменной =
Все переменные, входящие в выражение, должны быть
определены ранее в документе (должны иметь значения).
Пример:
a 0.27
b 2.4
c 0.8
c b
y ln
( cos ( a b c) )
c a b
y 0.877
22
23.
4. Стандартные и пользовательские функцииВ MathCAD могут использоваться стандартные
(встроенные) и определенными пользователем функции.
Стандартные функции разделены на категории
• математические
• векторные и матричные
• статистические
• аппроксимации и интерполяции
• решения алгебраических и дифференциальных
уравнений и систем
• доступа к внешним данным
и т.д.
23
24.
Для вставки функции в выражение используется командаВставка – Функция или инструмент f(x) на ПИ.
Для вставки часто используемых функций (sin(x), ln(x),
lg(x)=log(x) и др.) можно использовать ПИ Калькулятор.
Аргументы
тригонометрических
функций
должны
указываться в радианах. Для перевода аргумента из градусов в
радианы можно использовать встроенную переменную deg.
deg 0.017
180
Примеры:
sin( 30 * deg) 0.5
y 4.2 5i
Re( y) 4.2
Im( y) 5
24
25.
Для создания выражений с условиями используется функцияif ( условие, выражение1, выражение2),
которая возвращает выражение1, если значение логического
выражения в условии ИСТИНА (1) и выражение2 в
противном случае (ЛОЖЬ, 0).
В логическом выражении могут использоваться
• операции отношения (< , ≤ , >, ≥ , = , < >)
• логические операции И (٨), ИЛИ (٧), НЕ (¬)
Функции if могут быть вложенными, использоваться в
выражении1 и выражении2.
25
26.
Функции пользователя до обращения к ним должны бытьопределены.
Общий вид описания функции:
имя_функции (список формальных параметров):= выражение
Имя функции задается как любой другой идентификатор.
Формальные параметры (аргументы) функции разделяются
запятыми, они могут быть переменными, массивами,
функциями. В выражении все переменные кроме формальных
параметров должны быть определены до описания функции.
Обращение к функции со списком фактических параметров
может использоваться в любом выражении или слева от знака =
в операторе вычисления. Список фактических параметров
может содержать константы, переменные, выражения
26
27.
Пример 1.x1 1
x2 1
y1 1
z( x y) 2 atan( 3 x)
z x1 4 y2 4.084
y2 1
s 3
x y s
z( x2 1) 4.498
27
28.
Пример 2. Вычислить значения функции для несколькихзначений аргумента.
x ,
если x 0 ;
y ( x) x 1, если 5 x 10 ;
2
в ост. случаях.
x ,
2
y ( x) if x 0 x if 5 x 10 x 1 x
y ( 3) 3 y ( 5) 6 y ( 6) 7 y ( 11) 121
28
29.
5. Дискретные переменныеВ системе MathCad кроме простых переменных
существует понятие ранжированной или дискретной
переменной. Эта переменная имеет ряд значений (обычно
целых или вещественных), которые меняются от начального
значения до конечного с фиксированным шагом. Если такая
переменная используется в выражении, то значение
выражения вычисляется для каждого ее значения, и
результатов получается столько, сколько значений имеет
дискретная переменная.
Для создания дискретной переменной используется один
из операторов:
x:= xn .. xk
x:= xn, xn + ∆x .. xk
29
30.
гдеx – имя переменной,
xn – начальное значение переменной,
xk – конечное значение переменной,
∆x – шаг изменения переменной
.. – символ, указывающий на изменение переменной в
диапазоне (символ ; на клавиатуре, или
– в ПИ Матрица ).
Если второе значение не указывается (1 способ), то шаг
считается равным 1 (при xn<xk) или -1 (при xn>xk) . При
выводе значения дискретной переменной с помощью оператора
вычисления в документе появляется таблица значений.
30
31.
Дискретные переменные могут быть аргументами функций.Функция дискретного аргумента имеет множество значений,
каждое из которых соответствует определенному значению
дискретного аргумента. Т.е. выполняется табулирование
функции.
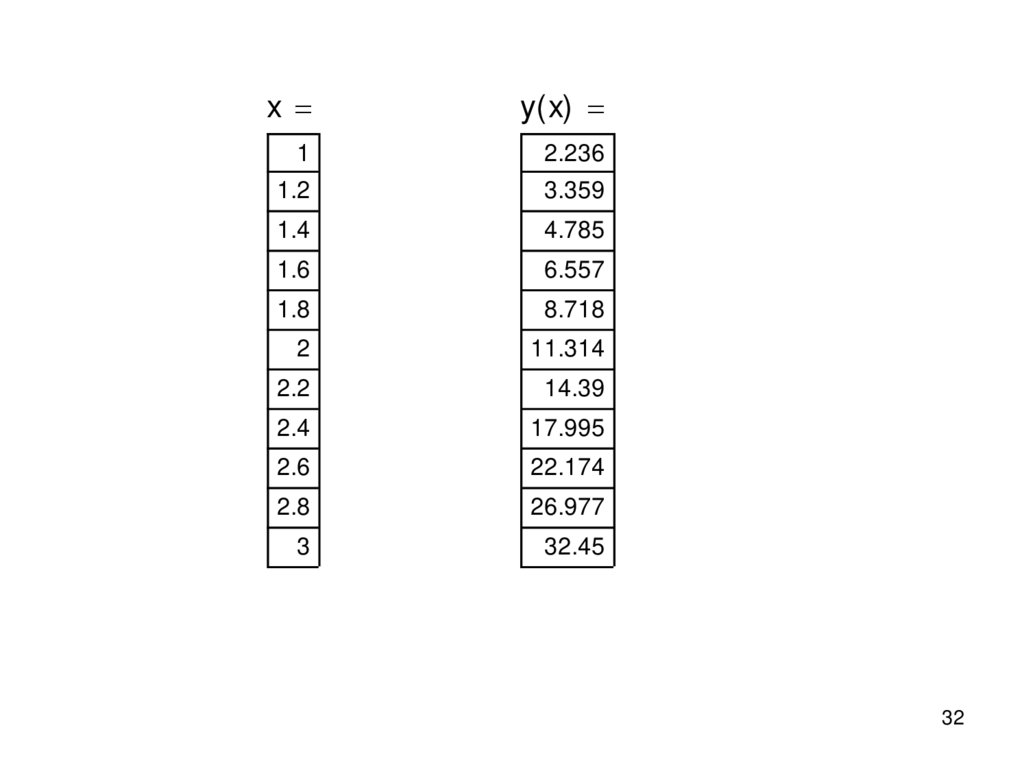
Пример 3.
x 1 1.2 3
xn 1
ИЛИ
xk 3
x 0.2
x xn xn x xk
2
2
y( x) x 4 x
31
32.
xy( x)
1
2.236
1.2
3.359
1.4
4.785
1.6
6.557
1.8
8.718
2
11.314
2.2
14.39
2.4
17.995
2.6
22.174
2.8
26.977
3
32.45
32
33.
6. Вычисление сумм, произведений, производных иинтегралов
Шаблоны для вычисления сумм, произведений,
интегралов, производных, пределов расположены в панели
инструментов исчисления (математического анализа)
33
34.
Порядок выполнения вычислений:1 способ:
• выбрать место для размещения выражения
• выбрать нужный шаблон в палитре щелчком мыши
• заполнить шаблон необходимыми данными
• нажать =
2 способ:
• задать переменную, включив в определяющее ее
выражение нужный шаблон
• заполнить шаблон необходимыми данными
• вычислить значение переменной с помощью оператора =
34
35.
Замечания:• можно заранее определить подынтегральную или
дифференцируемую функции, суммируемое выражение,
а затем использовать их в шаблонах
• значение производной можно вычислить как для
отдельных значений аргумента, так и для диапазона
значений, используя дискретную переменную
• при вычислении сумм и произведений можно
использовать шаблоны, включающие начальное и
конечное значение индекса и шаблоны, включающие
только имя индекса, задав его предварительно как
дискретную переменную
35
36.
Примеры:9
7
y ( x )
x 6
( x 7) ( x 3)
dx 0.321
x 6
( x 7) ( x 3)
9
s y ( x ) dx
7
s 0.321
36
37.
2y ( x ) x 25 x 5
d
y ( x1) 22.6
dx1
y1 ( x )
x1 1.2
d
x2 0.8
x 0.8
x2 25 x 5 26.6
dx
d
y (x)
y1 ( x1) 22.6
y1 ( x2) 26.6
dx
37
38.
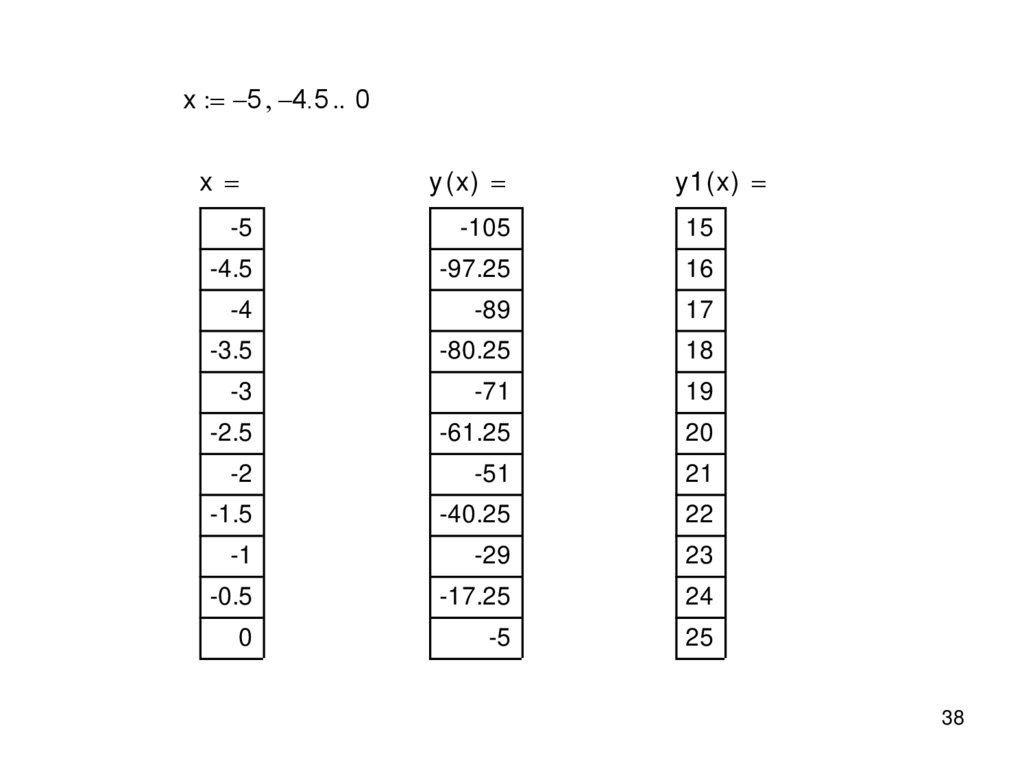
x 5 4.5 0x
y ( x)
y1 ( x )
-5
-105
15
-4.5
-97.25
16
-4
-89
17
-3.5
-80.25
18
-3
-71
19
-2.5
-61.25
20
-2
-51
21
-1.5
-40.25
22
-1
-29
23
-0.5
-17.25
24
0
-5
25
38
39.
8(i 3) (i 6) 48
i 1
i 1 8
y
(i 3) (i 6) y 48
i
ti ( i 3) ( i 6)
ti 48
i
9
i 4
( i 3)
i 3
i 2
2.778 10
12
39
40.
7. Векторы и матрицыВ системе MathCAD используются одномерные массивы
(векторы) и двумерные (матрицы).
Работа с
Матрица.
массивами
выполняется
с
помощью
ПИ
Индексы элементов массивов могут иметь только
целочисленные значения. Они могут начинаться с нуля (по
умолчанию) или другого целого числа, заданного значением
системной переменной ORIGIN.
Значение этой переменной может быть переопределено
непосредственно в документе с помощью операторов
локального или глобального присваивания.
ORIGIN 1
ORIGIN 1
40
41.
Векторы и матрицы можно задавать различными способами:• с помощью шаблона, используя команду
Вставка – Матрица или инструмент
ПИ Матрица
В появившемся окне задать размерность массива, нажать
ОК, а затем ввести элементы массива;
A
• как переменные с индексами, а элементы в массив ввести
перечислением, через запятую. Нижний индекс вводится
нажатием клавиши [ , либо щелчком на кнопке
ПИ
41
Матрица
42.
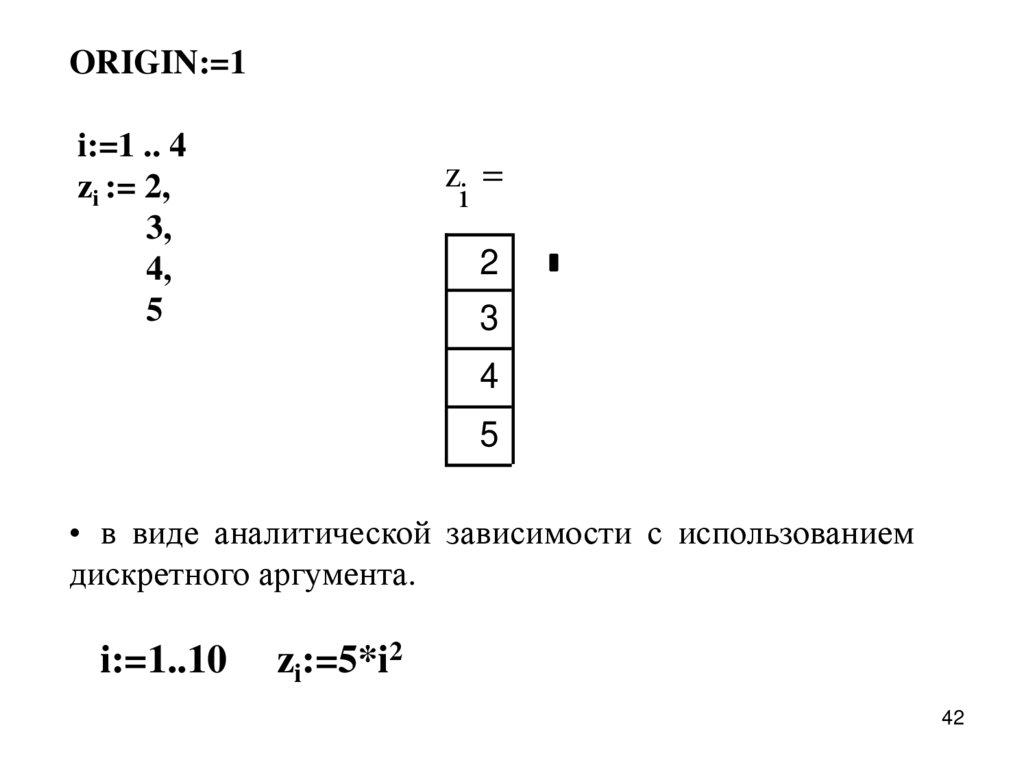
ORIGIN:=1i:=1 .. 4
zi := 2,
3,
4,
5
z
i
2
3
4
5
• в виде аналитической зависимости с использованием
дискретного аргумента.
i:=1..10
zi:=5*i2
42
43. Обращение к элементам матрицы M, вектора V
элементаммассива
столбцам
матрицы
строкам
матрицы
Vномер элемента M < номер столбца > Mномер строки,
Mномер строки,
индекс столбца
номер столбца
Примеры:
z1
A1,2
2
A
А2,i
• создать вектор из третьего столбца матрицы А:
ORIGIN 1
3
V1 A
43
44.
• найти произведение матрицы на вектор:35.5
A V2 34.5
20.5
• найти определитель матрицы:
A 41.5
44
45.
Параллельные вычисления, векторизацияБольшинство вычислений с дискретными переменными и
массивами строятся на принципе поэлементных вычислений.
Такие же действия можно выполнить с помощью операции
векторизации.
Векторизация – это применение
математических
операций и функций к каждому элементу массива поочередно.
1 3
A
4 9
4 3
A B
10
12
1 1.732
A
2 3
2 3
B
2 0
2 9
( A B)
8
0
45
46.
Системапозволяет
выполнять
рекуррентные
вычисления, когда следующий элемент массива вычисляется
через предыдущий по некоторому алгоритму.
i 1 3
pi 1 pi 2
p1 10
pi
10
12
14
46
47.
8. Программирование в MathCadСистема Mathcad позволяет использовать при вычислении
выражений, переменных и функций пользователя встроенный
язык программирования.
Для работы с программными фрагментами используется
панель
программирования,
включающая
следующие
инструменты (операторы):
Add Line – создание и расширение программного
фрагмента
– внутреннее, локальное присваивание
47
48.
if – условный оператор.Синтаксис:
выражение if условие
В условии записывается логическое выражение. Оно
формируется так же, как и в функции if.
Необходимо сначала вставить шаблон оператора, а
затем заполнять его элементы.
Если значение логического выражения – ИСТИНА
(условие выполняется), то результатом является значение
выражения.
–
оператор
иначе, используется
совместно с оператором if для выполнения действий в случае
невыполнения условия
otherwise
Синтаксис:
выражение otherwise
48
49.
for – оператор цикла с заданным числом повторений.Синтаксис:
for <параметр_цикла> <диапазон изменения>
< тело цикла >
Диапазон изменения параметра цикла задается с помощью
дискретной переменной или вектора. Параметр цикла можно
использовать в программном фрагменте.
Примеры заголовков цикла:
for i 1..n
for z 1,1.5..10
for x V
49
50.
while – цикл с предусловием.Синтаксис:
while условие
< тело цикла >
Тело цикла выполняется до тех пор, пока логическое
выражение в условии имеет значение ИСТИНА
50
51.
Создание программного фрагментав ПИ программирования выбрать инструмент Add line. На
экране появится следующий шаблон:
поле 1
поле 2
в поле1 ввести первый оператор, для вставки
дополнительных полей ввода использовать инструмент Add
line
в последнем поле (поле 2) определить возвращаемое
значение
(иначе
возвращаться
будет
последнее
вычисленное значение)
51
52.
Переменные, определенные в программном фрагменте,являются локальными и их значения не могут
использоваться в документе вне этого фрагмента.
В программном фрагменте могут использоваться
переменные,
значения
которых
определены
до
программного фрагмента.
Группа операторов, соответствующая составному
оператору на языке Delphi, формируется добавлением
полей ввода с помощью инструмента Add line в теле
циклов и в выражениях операторов if и otherwise.
52
53.
Примеры программных фрагментов1. Линейные алгоритмы
1.1. вычисление значения
выражения
a 3
5
b 4
2
a b
1.2. вычисление значения
переменной
d 3
r
s 4
2
2
d s
2
2
r 7
53
54.
1.3. вычисление значения функции:y ( x1 x2 y1 y2)
r
2
( x2 x1) ( y2 y1)
2
r
y ( 4 0 0 3) 5
54
55.
2. Разветвляющиеся алгоритмыВычислить значения функции y(x). Вид функции:
x ,
если x 0 ;
y ( x) x 1, если 5 x 10 ;
2
в ост. случаях.
x ,
Фрагмент документа MathCad
Описание (объявление функции):
y ( x)
x
if x 0
x 1 if 5 x 10
Вычисление значений функции
(обращение к функции):
y( 6) 7
y( 10) 11
2
x
otherwise
y( 11) 121
55
56.
3. Циклические алгоритмыПри реализации алгоритмов работы с массивами (особенно
при изменении элементов массива и формировании новых
массивов) результат лучше формировать как функцию,
аргументом которой является исходный массив.
Для определения размерности одномерного массива x
можно использовать функцию length(x), для определения
количества строк двумерного массива функцию rows(x),
количества столбцов – cols(x) или вводить дополнительные
параметры функции, определяющие размерность массивов.
Описание функции:
sum (x) :=……
sum (x, n) :=…..
max (x, n, m) :=
Обращение к функции:
sum (y) =
sum (y, 8) =
max (A, 5, 3) =
56
57.
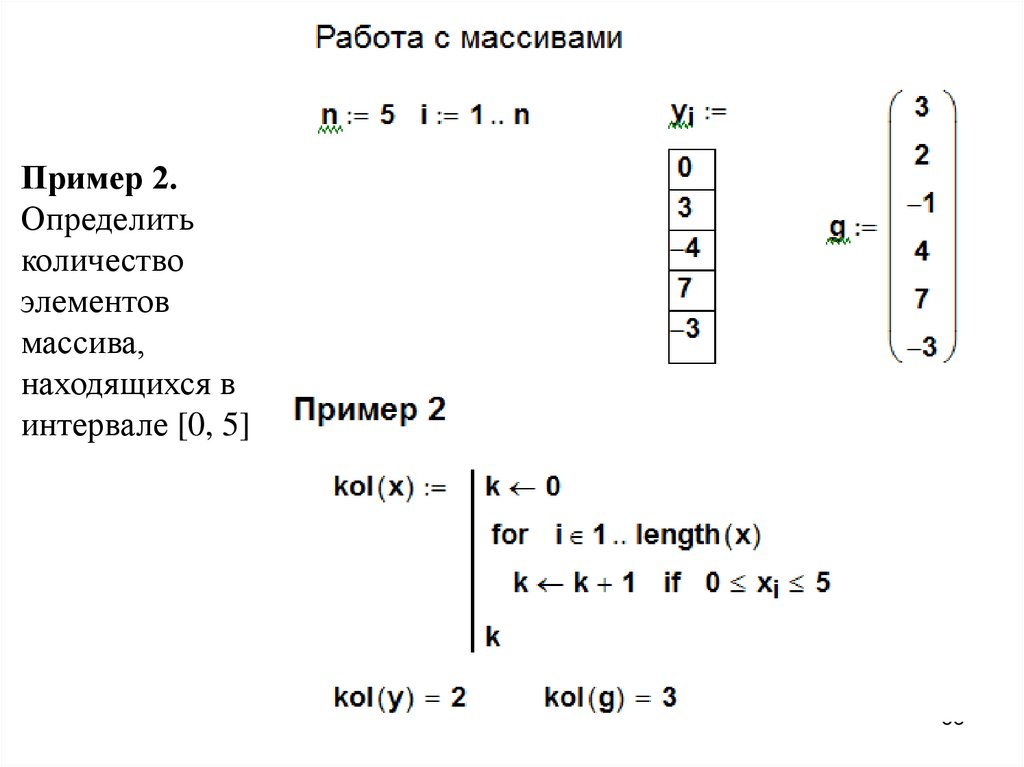
60Пример 1. Вычислить
i 1
sum
1
i
i
s 0
for i 1 60
1
s s
i
i
sum 315.227
Проверка с помощью встроенного шаблона:
60
i 1
1
i
i 315.227
57
58.
Пример 2.Определить
количество
элементов
массива,
находящихся в
интервале [0, 5]
58
59.
Пример 3. Определить количество элементов массива,находящихся в интервале (a, b)
59
60.
4.Вычислить
сумму
элементов массива,
находящихся
на
местах c четными
номерами
и
больших,
чем
среднее
арифметическое всех
элементов массива.
60
61.
Пример 5.Поменять
местами в
массиве
минимальный
элемент с
последним.
61
62.
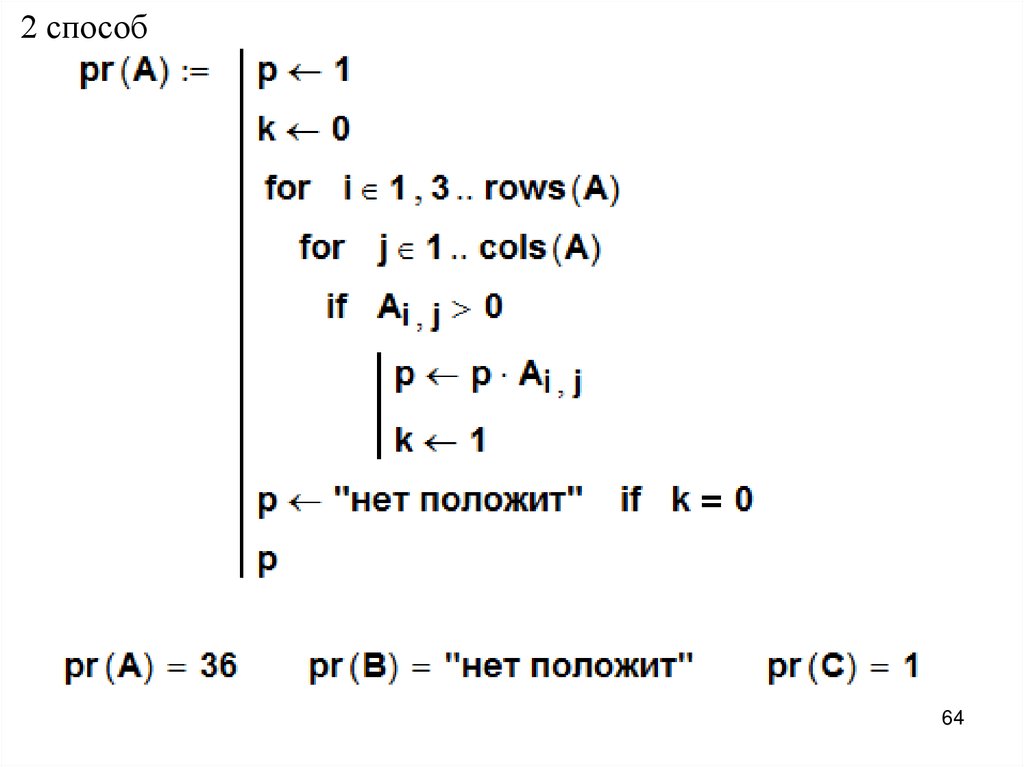
6. Вычислить произведение положительныхэлементов матрицы, расположенных в строках с
нечетными номерами.
62
63.
6364.
2 способ64
65.
9. Графические возможности системы MathCAD(м/ук № 2564)
Графические области делятся на три основных типа –
двумерные графики, трехмерные графики и импортированные
графические образы. Для построения графиков используются
шаблоны, которые находятся в панели графики или в меню
Вставка – График….
9.1. Построение двумерных графиков
Для построения простого двумерного графика в декартовой
системе координат используется инструмент X-Y Plot. При его
выборе появляется шаблон, в котором на оси Y задаются имена
функций, разделенные запятыми, а на оси X – имена
аргументов, разделенные запятыми.
65
66.
График строится по точкам, в которых заданы значенияаргумента, и которые могут отображаться графическими
символами (квадраты, кружки и т.д.).
Точки соединяются линиями разных видов (сплошной,
пунктирной и т. д.).
Можно указать минимальные и максимальные значения по
осям, в противном случае они будут выбраны автоматически,
но, при необходимости, могут быть изменены.
66
67.
Пример 1. Аргумент задан дискретной переменной,функции – в аналитическом виде.
Последовательность действий для построения графика:
определить дискретную переменную – аргумент:
x:=xn, xn+∆x .. xk
задать вид функций:
y1(x):=
y2(x):=
вставить в документ шаблон X-Y Plot
указать в шаблоне аргумент (x) и функции (y1(x), y2(x))
выйти из области графика
67
68.
Пример 2. Аргумент и функции заданы векторами• определить переменную ORIGIN и дискретную
переменную – индекс
ORIGIN:=1 i:=1..10
• определить векторы (любым способом)
xi:=1,3,5
y:=…
• вставить в документ шаблон X-Y Plot
• указать в шаблоне аргумент (xi) и функцию (yi)
• выйти из области графика.
68
69.
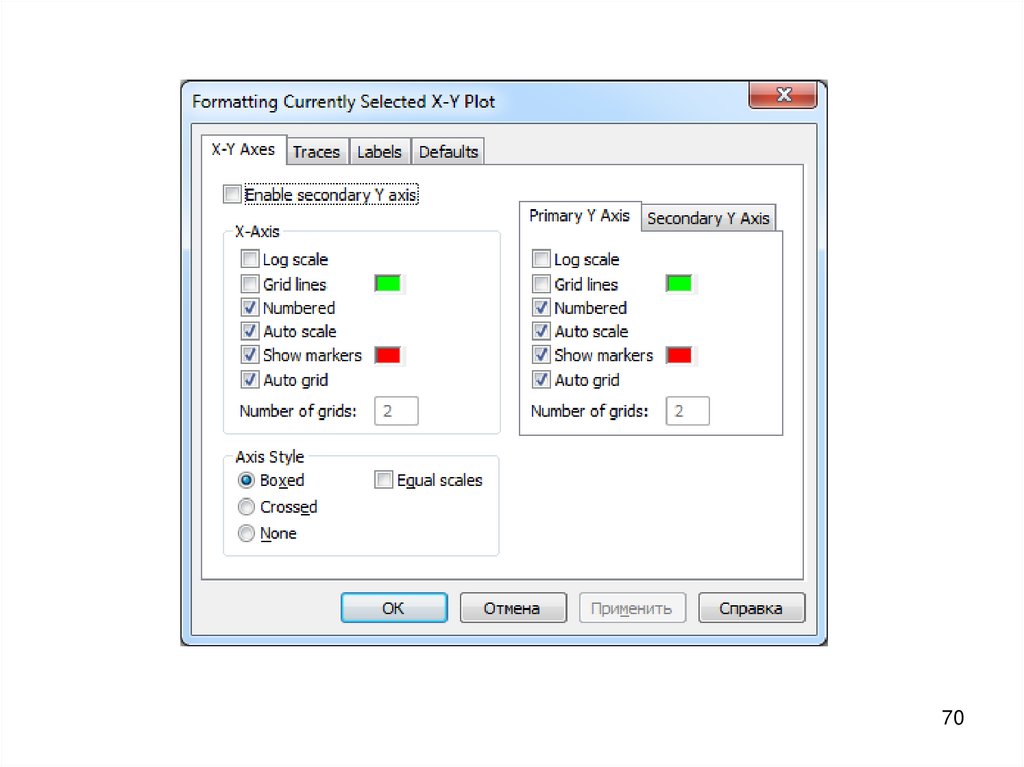
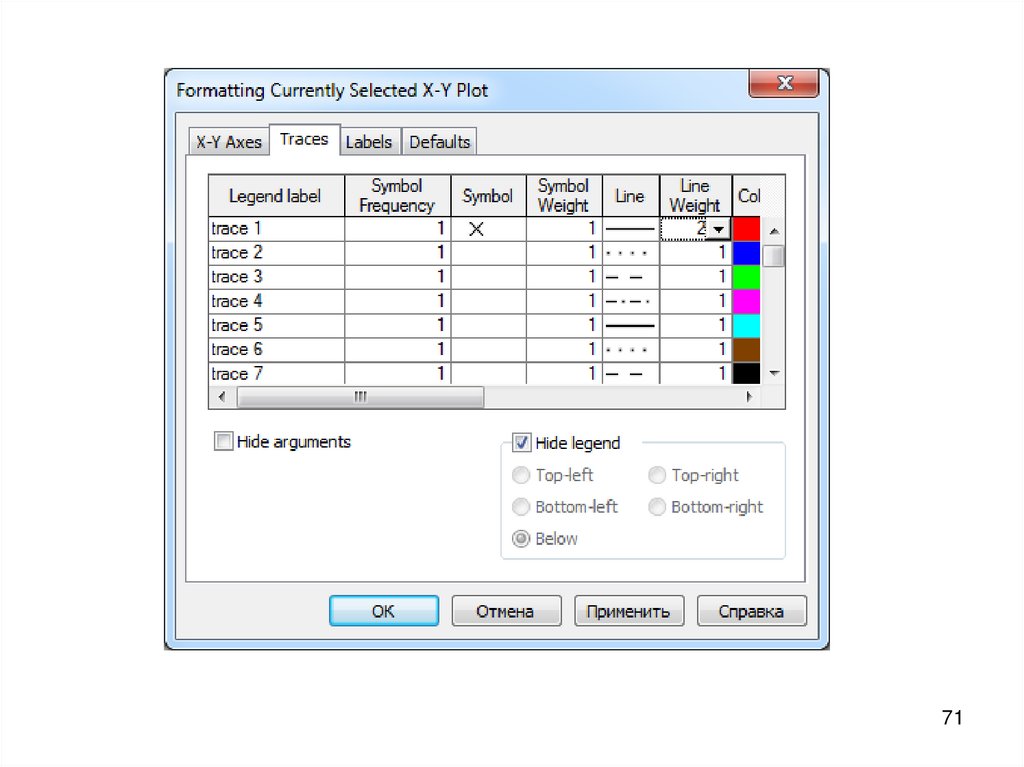
9.2. Форматирование графикаФорматирование
графика
выполняется
в
ДО
Форматирование текущего X-Y графика, которое открывается
командой Формат – График (для выделенного графика) или
двойным щелчком в области графика.
ДО имеет четыре вкладки:
форматирование осей
форматирование линий графиков
установка надписей
установка режимов по умолчанию
69
70.
7071.
7172.
На вкладке X-Y оси можно установить линии координатнойсетки, количество делений на осях, оцифровку осей, установить
маркеры для нанесения фоновых линий.
При форматировании линий графиков можно изменить вид,
цвет, толщину линий, наличие и вид маркеров (символов) в
узловых точках.
Нанесение
фоновых
линий
(вертикальные
горизонтальные линии, параллельные осям координат):
и
на вкладке форматирования осей установить режим
Show Markers (Показать маркеры); на каждой оси
появятся два маркера
• в маркеры ввести
фоновых линий
необходимые
значения
координат
72
73.
Для определения координат точек графика можноиспользовать метод трассировки. Для этого выделить график
и выполнить команду Формат – График – Трассировка…,
выделить нужную точку и с помощью буфера обмена
скопировать ее координаты в координаты фоновых линий на
графике.
Если отключить режим Track Data Points (следовать
линиям графиков), то можно определить координаты любой
точки в графической области.
Для
увеличения
необходимой
области
графика
используется команда Формат – График – Масштаб…
73
74.
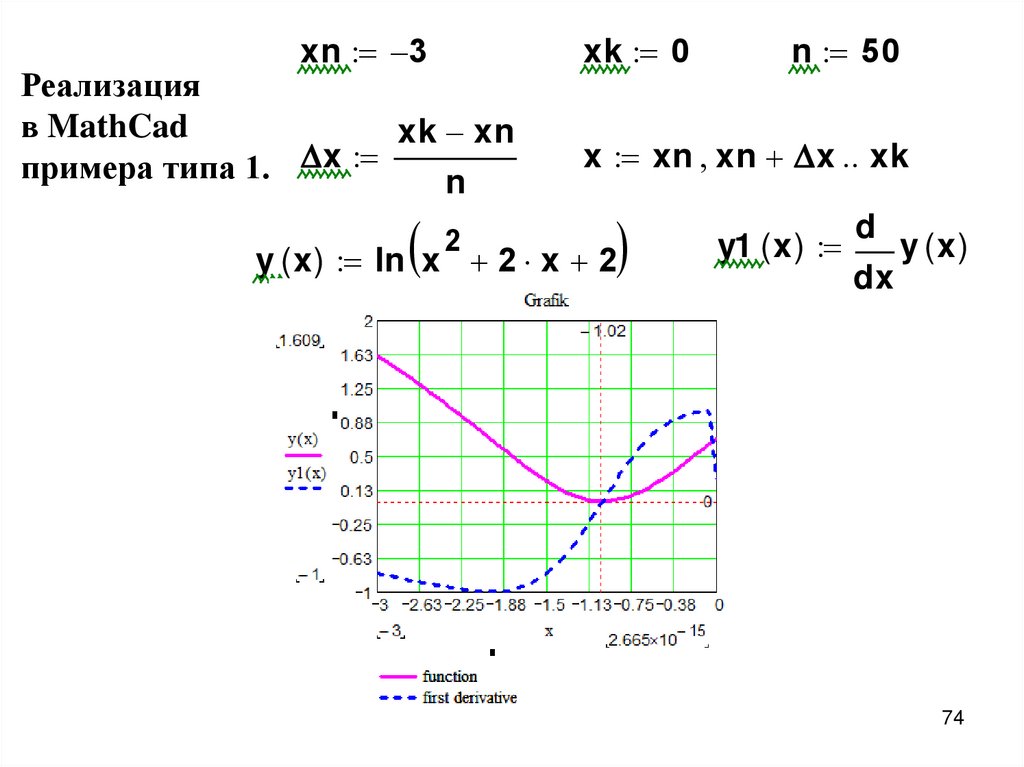
xn 3Реализация
в MathCad
xk xn
примера типа 1. x
n
2
xk 0
n 50
x xn xn x xk
y ( x ) ln x 2 x 2
y1 ( x )
d
y (x)
dx
74
75.
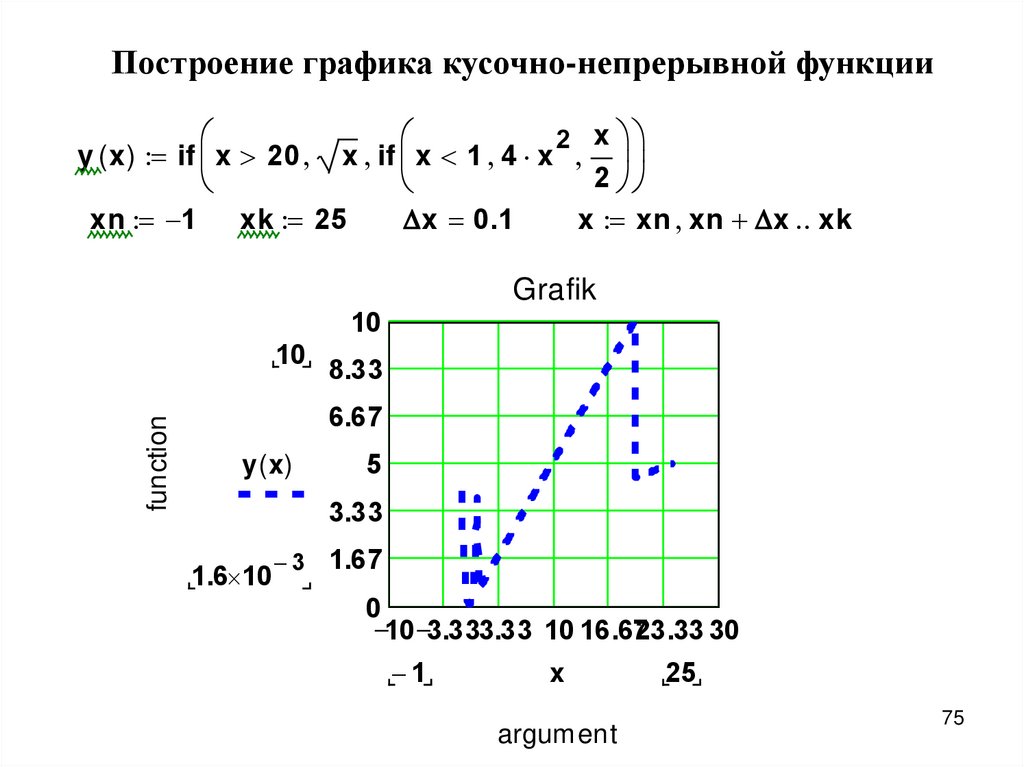
Построение графика кусочно-непрерывной функции2 x
y ( x ) if x 20 x if x 1 4 x
2
xn 1
xk 25
x 0.1
x xn xn x xk
Grafik
10
function
10
8.33
6.67
y ( x)
5
3.33
1.6 10
3
1.67
0
10 3.333.33 10 16.6723.33 30
1
x
argument
25
75
76.
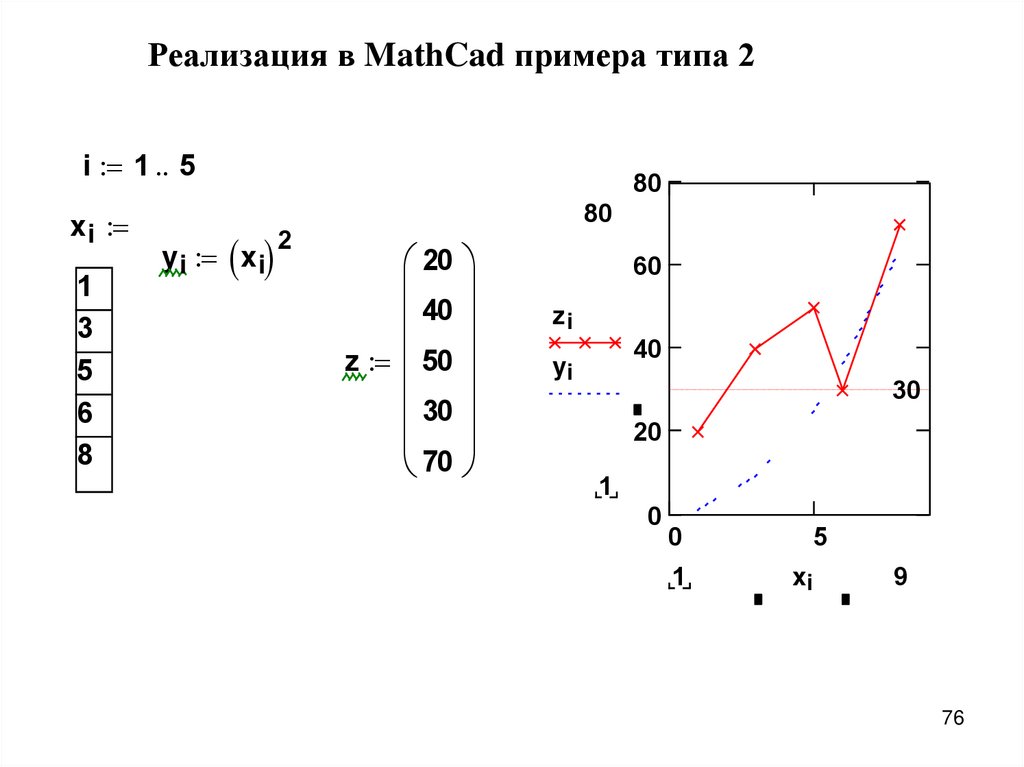
Реализация в MathCad примера типа 2i 1 5
x i
1
3
5
6
8
y i x i
80
2
80
20
40
z 50
30
70
60
zi
40
yi
30
20
1
0
80
0
1
5
xi
9
60
40
30
76
77.
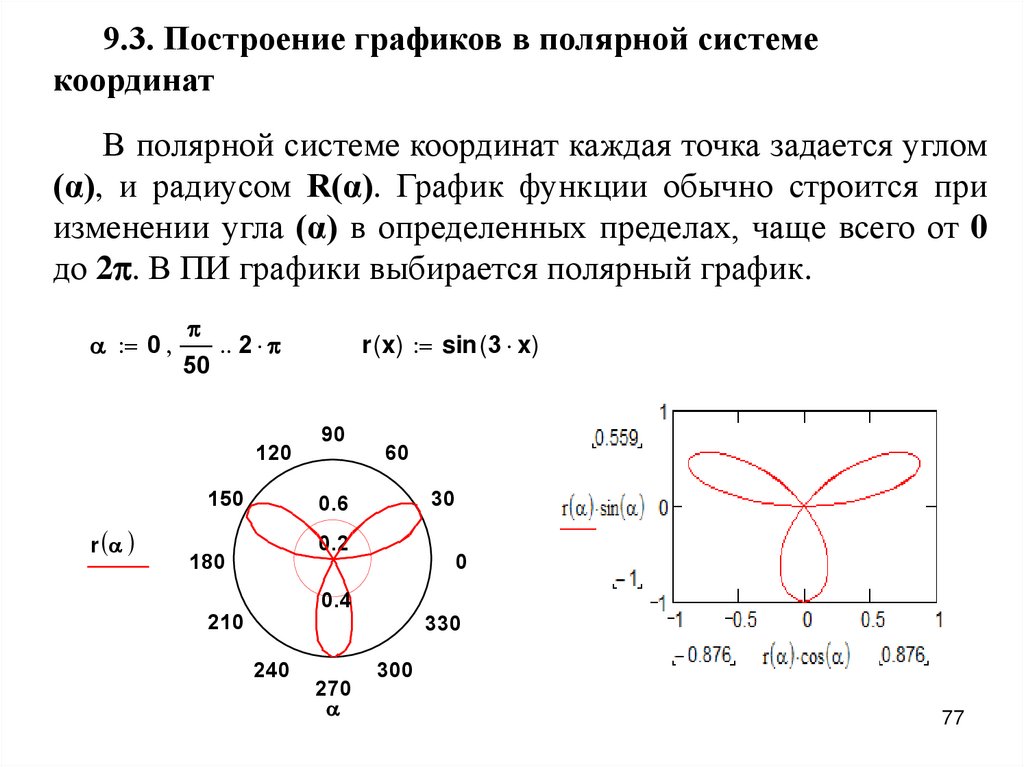
9.3. Построение графиков в полярной системекоординат
В полярной системе координат каждая точка задается углом
(α), и радиусом R(α). График функции обычно строится при
изменении угла (α) в определенных пределах, чаще всего от 0
до 2 . В ПИ графики выбирается полярный график.
0
2
50
120
150
r
r ( x) sin ( 3 x)
90
60
30
0.6
0.2
180
0
0.4
210
240
270
330
300
77
78.
9.4. Построение трехмерных графиковТрехмерные или 3D-графики отображают функцию двух
переменных вида Z(X,Y). Для построения трехмерная
поверхность Z(X,Y) должна быть предварительно задана
матрицей координат по оси Z. Номера строк и столбцов
матрицы будут использоваться как координаты по осям X, Y.
Значения аргументов могут предварительно определяться в
зависимости от номеров строк и столбцов. Шаблон содержит
единственный темный прямоугольник, в который заносится имя
матрицы со значениями координат по оси Z.
Другой способ определения трехмерных поверхностей – это
формирование трех матриц – X, Y и Z с координатами точек
поверхности. В этом случае в шаблоне указываются все
матрицы координат в виде X, Y, Z
78
79.
Трехмерные графики. Формирование исходных данныхПример 1
x 1 20
Пример 2
Пример 3
y 1 20 Mx y x sin( y 0.5)
i 1 10
j 1 15
x i 3 0.15 i
y j 2 0.2 j
2
2
Mi j cos x i y j
1 2 3
0 0 0
1 2 2
X 1 2 3 Y 1 1 1 Z 1 2 2
1 2 3
2 2 2
1 2 2
79
80.
10. Решение уравнений и систем уравненийТочное решение уравнений не всегда можно найти
аналитическими методами. При этом такие уравнения могут
решаться численными методами с заданной точностью. При
решении уравнений могут применяться различные методы. К
ним относятся:
метод итераций
метод касательных
метод хорд
метод половинного деления и т.д.
В MathCad в основном используются методы итераций и
половинного деления, точность решения определяется
системной переменной TOL.
80
81.
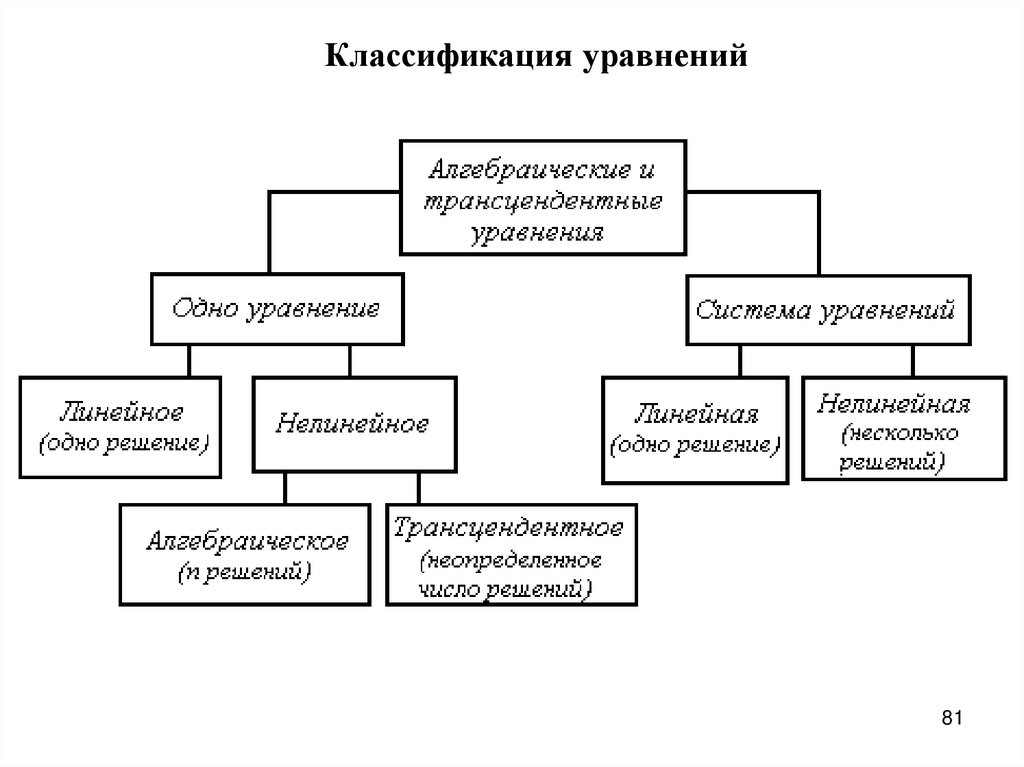
Классификация уравнений81
82.
10.1. Решение линейных и нелинейных уравненийДля уравнений вида f(x)=0 решение находится с
помощью функции root.
Синтаксис функции:
root ( f(х), х)
где
f(х) – функция описывающая левую часть уравнения;
х – имя переменной, относительно которой решается
уравнение.
82
83.
Функция root находит корни уравнения итерационнымметодом, поэтому перед ее использованием необходимо задать
начальное приближение (значение) искомой переменной х.
Функция позволяет найти как вещественные, так и
комплексные корни. Во втором случае начальное приближение нужно задать как комплексное
число. Если уравнение не имеет вещественных корней, то комплексные корни будут найдены и при
вещественном начальном приближении.
В зависимости от выбранного приближения будут найдены
разные корни уравнения, близкие к начальному приближению.
Для определения начальных
использовать графический метод.
приближений
можно
Необходимо построить график функции f(x) и определить
примерно точки пересечения графика функции с осью Х (можно
провести фоновую линию y=0).
83
84.
Можно определить функцию пользователя, аргументомкоторой будет начальное приближение корня
z(x):=root(f(x),x)
В этом случае значения функции z(x) для разных начальных
приближений и будут значениями корней уравнения f(x)=0.
Иногда возникает необходимость многократного решения
уравнения f(a,x)=0 при изменении одного из параметров.
Тогда можно определить функцию пользователя, аргументом
которой будет значение параметра и, возможно, начальное
приближение корня
z(a, x):=root ( f(a,x), x)
84
85.
Если после многих итераций Mathcad не находитподходящего
приближения,
то
появится
сообщение
отсутствует сходимость.
Такой результат
причинами:
может
быть
вызван
следующими
• уравнение не имеет корней
• корни уравнения расположены далеко от начального
приближения
• функция f(x) имеет разрывы между начальными
приближениями и корнями
Для изменения точности, с которой функция root ищет
корень, нужно изменить значение системной переменной
TOL. Если значение TOL увеличивается, функция root
будет сходиться быстрее, но ответ будет менее точен. Если
значение TOL уменьшается, то функция root будет сходиться
85
медленнее, но ответ будет более точен.
86.
Пример 1. Решить уравнение3
x 2 x 1
0
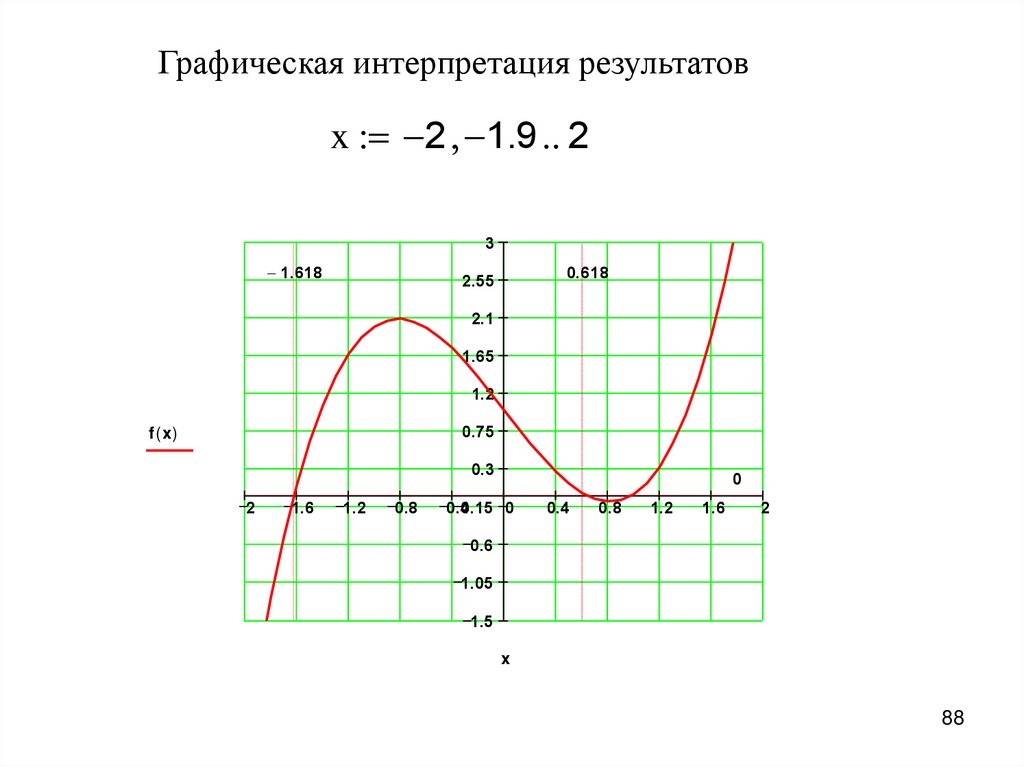
и выполнить графическую интерпретацию результатов.
3
f ( x) x 2 x 1
x 2
root ( f ( x) x) 1
x 0
root ( f ( x) x) 0.618
x1 3
z root ( f ( x1) x1)
z 1.618
86
87.
Длявыполнения
графической
интерпретации
результатов решения уравнения f(x)=0 необходимо:
• задать аргумент функции х (дискретную переменную) в
минимальном диапазоне, включающем все найденные
корни уравнения
• построить график функции f(x)
• провести фоновые линии в точках, совпадающих с
найденными значениями корней уравнения
Фоновые линии должны пересечься с графиком функции в
точках пересечения графика с осью Х (это и есть корни
уравнения, в них f(x)=0).
87
88.
Графическая интерпретация результатовx 2 1.9 2
3
1.618
0.618
2.55
2.1
1.65
1.2
0.75
f ( x)
0.3
2
1.6
1.2
0.8
0
0.4
0.15 0
0.4
0.8
1.2
1.6
2
0.6
1.05
1.5
x
88
89.
Зависимость решения от значения переменной TOLx1 3
x2 0
x3 5
TOL 0.01
z( x) root ( f ( x) x)
z( x1) 1.6194
z( x2) 0.6099
z( x3) 1.001
TOL 0.00001
z( x) root ( f ( x) x)
z( x1) 1.618
z( x2) 0.618
z( x3) 1
89
90.
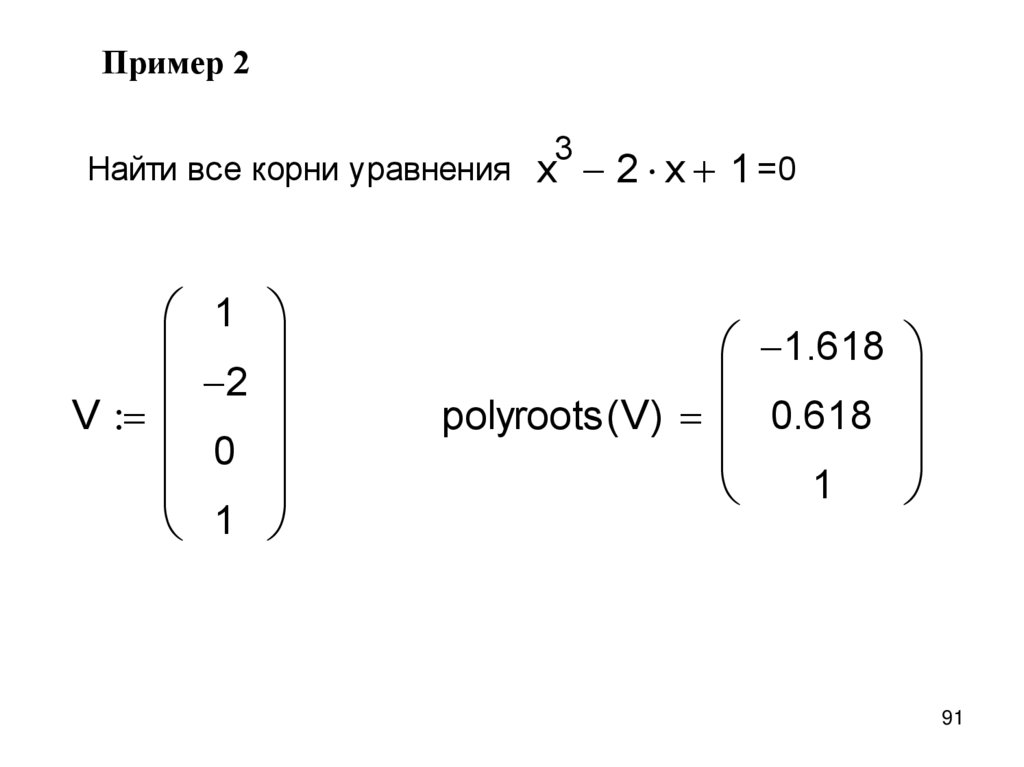
Для нахождения корней полинома видаa n x n ... a 2 x 2 a1 x a0
используется функция polyroots. В отличие от функции root
polyroots не требует начального приближения и возвращает
сразу все корни, как вещественные, так и комплексные.
Общий вид функции
polyroots(V)
где V – вектор коэффициентов полинома
размерности n+1, начиная с а0
n – степень полинома
a0
a1
V
......
an
Функция возвращает вектор длины n, состоящий из корней
90
полинома.
91.
Пример 2Найти все корни уравнения
1
2
V
0
1
3
x 2 x 1 =0
1.618
polyroots ( V)
0.618
1
91
92.
Пример 3. Решить нелинейное уравнениеx 1
sin( 2 x)
x 2
f ( x) x 1 sin( 2 x)
root( f ( x) x) 1.288
Нельзя использовать функцию polyroots для решения
нелинейных уравнений, но можно решать их блочным
методом как системы уравнений, состоящих из одного
92
уравнения.
93.
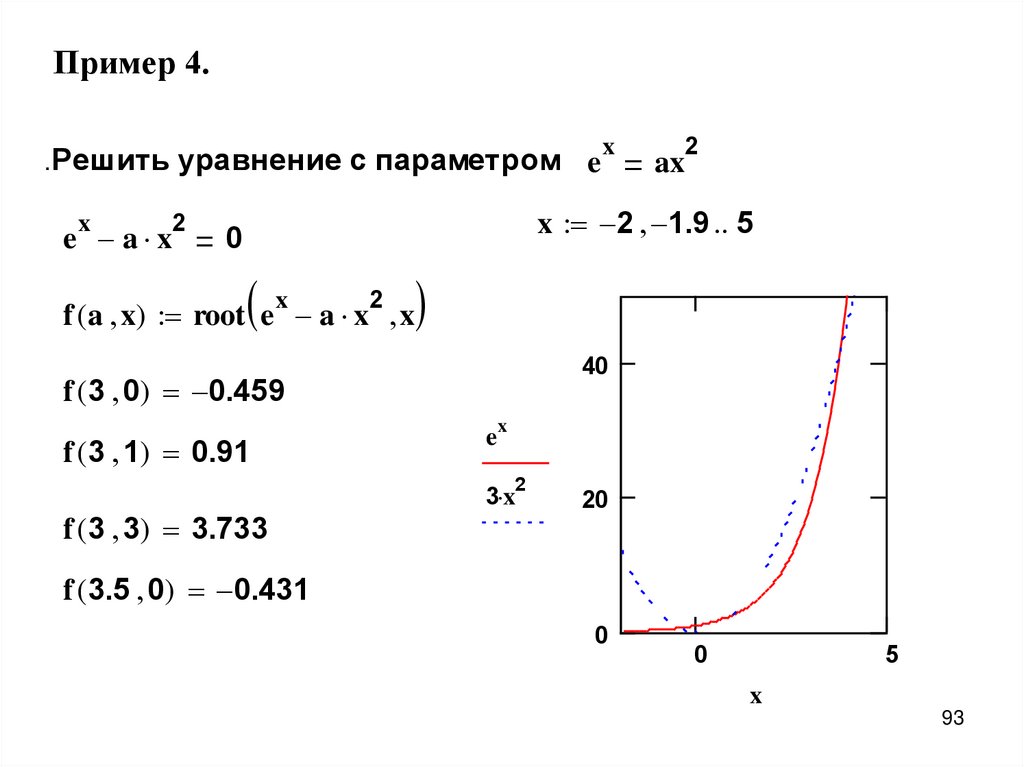
Пример 4.. Решить уравнение с параметром
x
2
e a x
e
x
2
ax
x 2 1.9 5
0
x
2
f ( a x) root e a x x
40
f ( 3 0) 0.459
f ( 3 1) 0.91
e
x
2
f ( 3 3) 3.733
3 x
20
f ( 3.5 0) 0.431
0
0
5
x
93
94.
10.2. Решение систем уравненийMathCAD дает возможность решать системы уравнений и
неравенств численными методами. Максимальное число
уравнений равно 50.
Наиболее распространенным и универсальным является
блочный метод. Для решения системы этим методом
необходимо выполнить следующее:
• задать начальное приближение для всех неизвестных,
входящих в систему уравнений
• ввести ключевое слово Given (НЕ ТЕКСТОВАЯ ОБЛАСТЬ),
оно указывает, что далее следует система уравнений
• ввести уравнения и неравенства в любом порядке. Для ввода
символа = в уравнении используется знак логического
равенства (Ctrl = или ПИ). Между левыми и правыми частями
неравенств может стоять любой из символов < >
94
95.
• ввести выражение, которое включает функцию Find в одномиз следующих видов:
Find (x1, x2,…) = где x1, x2… - неизвестные системы
x := Find (x1, x2,…), где х – вектор решений системы
f (a, b, c, …) := Find (x1, x2, x3, …), если необходимо
многократно решать систему уравнений для различных
значений
некоторых
параметров
a,
b,
c,…,
непосредственно входящих в систему уравнений
f (x1, x2, x3, …) := Find (x1, x2, x3, …), если необходимо
найти решение при различных начальных приближениях
95
96.
Число аргументов функции Find должно быть равно числунеизвестных.
Решающим блоком – называется часть документа,
расположенная между ключевыми словами Given и Find.
Внутри блока недопустимы символы , дискретные
переменные или выражения, содержащие дискретный аргумент
в любой форме, неравенства вида a<b<c, вложенные блоки
решения уравнений.
При использовании функции Find находится точное
решение системы уравнений (с учетом значения переменной
TOL).
Если Mathcad не может найти решение, то появляется
сообщение Решение не найдено.
96
97.
Такой результатпричинами:
может
быть
вызван
следующими
• система не имеет решения
• для уравнений, которые не имеют вещественных
решений, в качестве начального приближения взяты
вещественные числа и наоборот
• возможно, поставленная задача не может быть решена с
заданной точностью. Можно
увеличить значение
переменной TOL и попытаться найти решение
97
98.
Приближенное решение системы можно найти спомощью функции Minerr, которая использует тот же
алгоритм поиска решения. Если в результате поиска не
может быть получено дальнейшее уточнение текущего
приближения, Minerr возвращает это приближение.
Функция Find в этом случае возвращает сообщение об
ошибке.
Правила использования функции Minerr такие же, как и
функции Find. Общий вид функции
Minerr (x1, x2, ...)
При использовании функции Minerr необходимо всегда
включать дополнительную проверку найденного решения
(подставлять найденное решение в исходную систему
уравнений).
98
99.
Решение систем линейных уравненийСистема n линейных алгебраических уравнений с n
неизвестными х1, х2, …, хn
a11 x1 a12 x 2 ... a1n x n b1 ,
a 21 x1 a 22 x 2 ... a 2n x n b2 ,
. . . . . . . .
a n1 x1 a n2 x 2 ... a nn x n bn .
может быть записана в матричном виде Aх=B , где
a11 a12
a
21 a22
A
an1 an2
a1n
a2n
,
ann
x1
x2
x
,
...
xn
b1
b2
B
...
bn
99
100.
Если определитель матрицы А не равен нулю, то системаимеет единственное решение.
Для решения систем линейных уравнений можно
использовать кроме блочного метода и другие методы,
например, метод Крамера и матричный метод.
Системы линейных уравнений удобно решать с помощью
стандартной функции lsolve(A, B) – где A – матрица
коэффициентов, B – вектор свободных членов. Функция
возвращает вектор из n элементов – решение системы.
Пример 5. Решить разными методами систему уравнений
3x1 x2 7
2 x1 3x2 1
100
101.
а) метод КрамераORIGIN:=1
3 1
A
2 3
7
B
1
7 1
A1
1 3
A2 A
x1
A1
A
x1 2
2
A2
B
x2
A2
A
x2 1
101
102.
b) блочный методx1 1
x2 1
Given
3 x1 x2
2 x1 3 x2
7
1
x Find ( x1 x2)
2
x
1
102
103.
c) матричный методx A
1
B
2
x
1
d) с помощью функции lsolve
2
lsolve ( A B)
1
103

























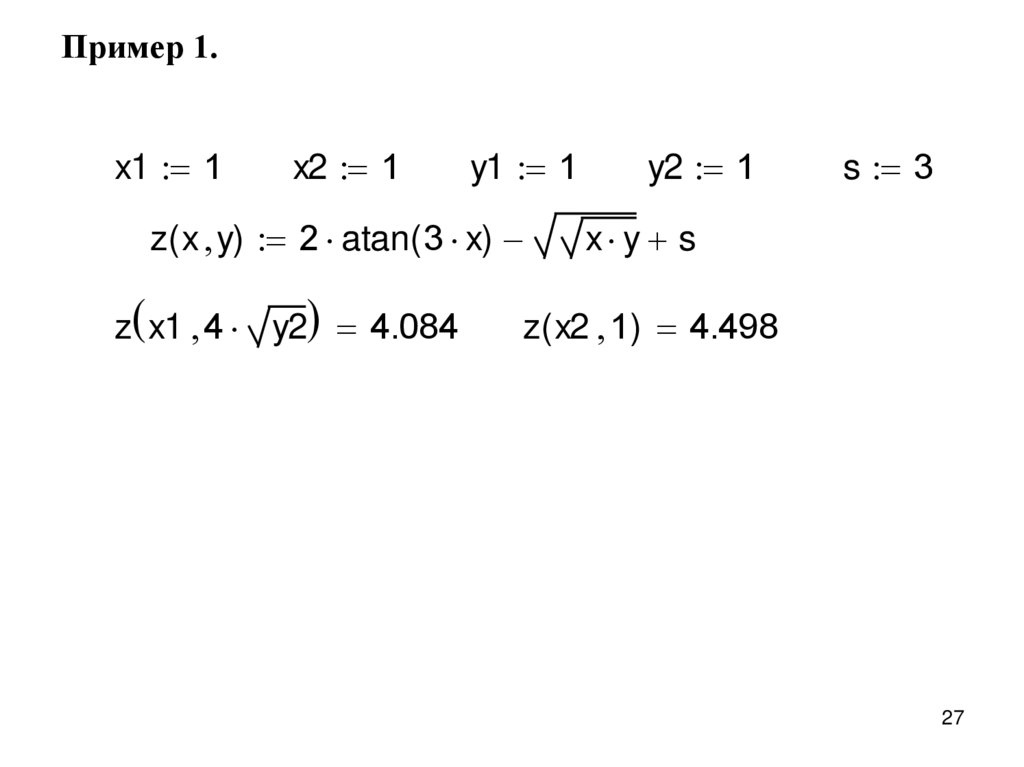








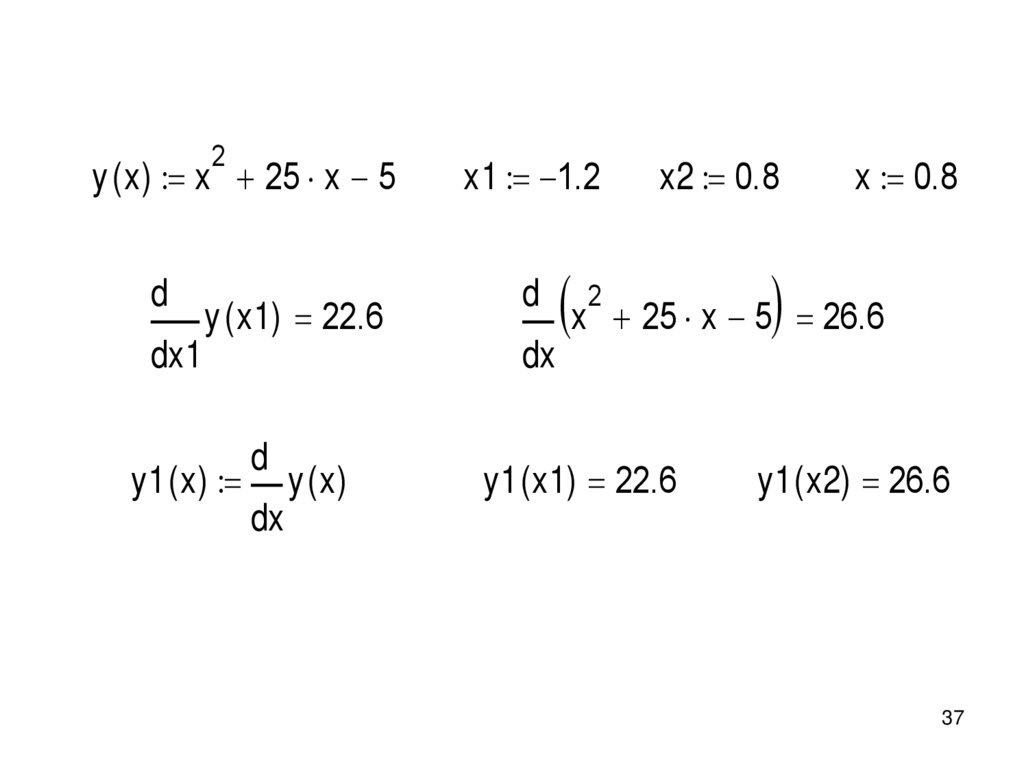
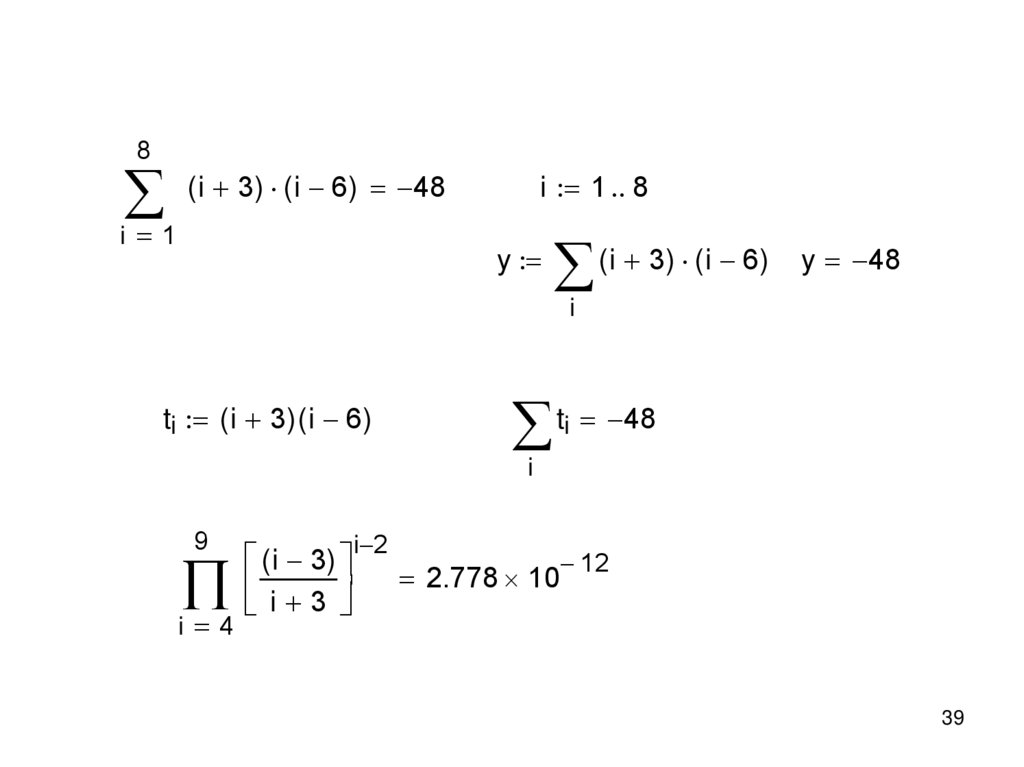



















































 Программное обеспечение
Программное обеспечение








