Похожие презентации:
Формула бинома Ньютона. Свойства биноменальных коэффициентоа
1.
2.
НЬЮТОН - английский математик,механик, астроном и физик, создатель
классической механики. Разработал
дифференциальное и интегральное
исчисления. Открыл дисперсию света,
исследовал интерференцию и
дифракцию, развивал корпускулярную
теорию света. Построил зеркальный
телескоп. Сформулировал основные
законы классической механики. Открыл
закон всемирного тяготения, создал
теорию движения небесных тел, создав
основы небесной механики.
1643-1727 г.г.
3. Бином Ньютона.
• «Би»-удвоение, раздвоение …• «Ном»(фран. nombre) –номер,
нумерация.
• «Бином» -»два числа»
4. Степени суммы двух чисел:
а в а в;2
2
2
а в а 2 ав в ;
3
2
2
2
3
а в а 3 а в 3 ав в
1
5. В теории многочленов часто двучлены называют биномами.
6. Биномиальная формула Ньютона.
1 n 1n
2 n 2 2
n
(a b) a C a b C a b ...
n
k n k k
n
n
C a b ... b
n
7. Степени суммы двух чисел:
а в С а в С а в ;1
0 1 0
1
1 0 1
1
а в С а в С а в С а в ;
2
0 2 0
2
1 1 1
2
2 0 2
2
а в С а в С а в С а в С а в ;
3
0 3 0
3
1 2 1
3
2 1 2
3
3 0 3
3
8. Правило Паскаля:
Сn
m 1
C
n 1
m
C
n
m
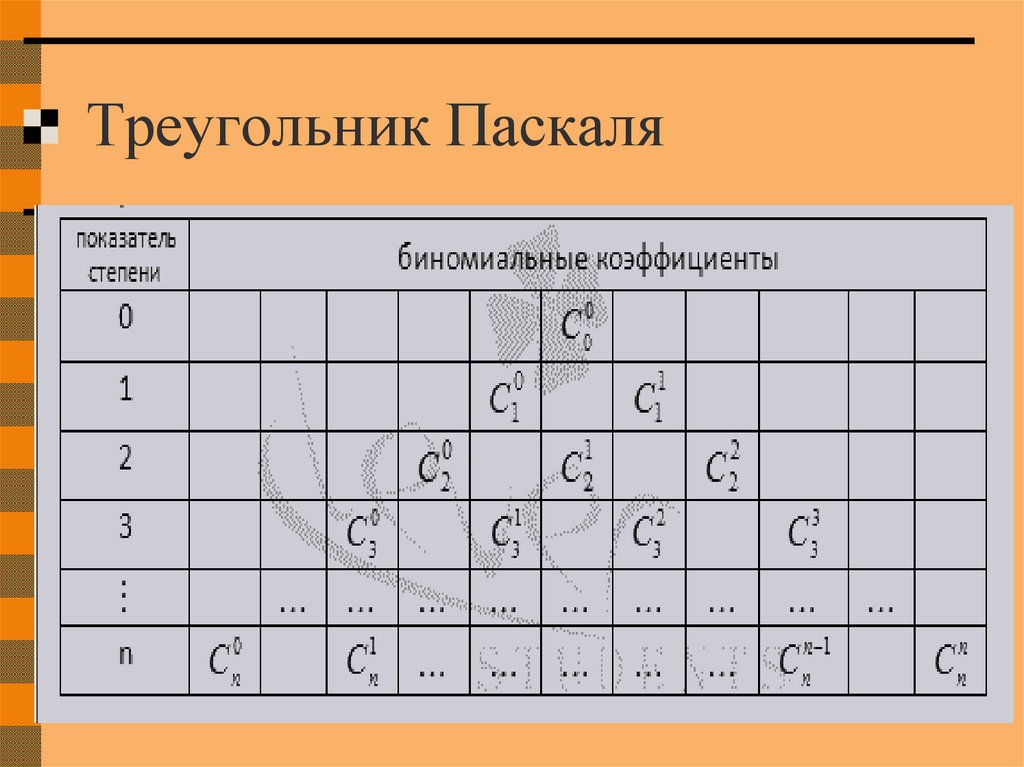
9. Треугольник Паскаля
10.
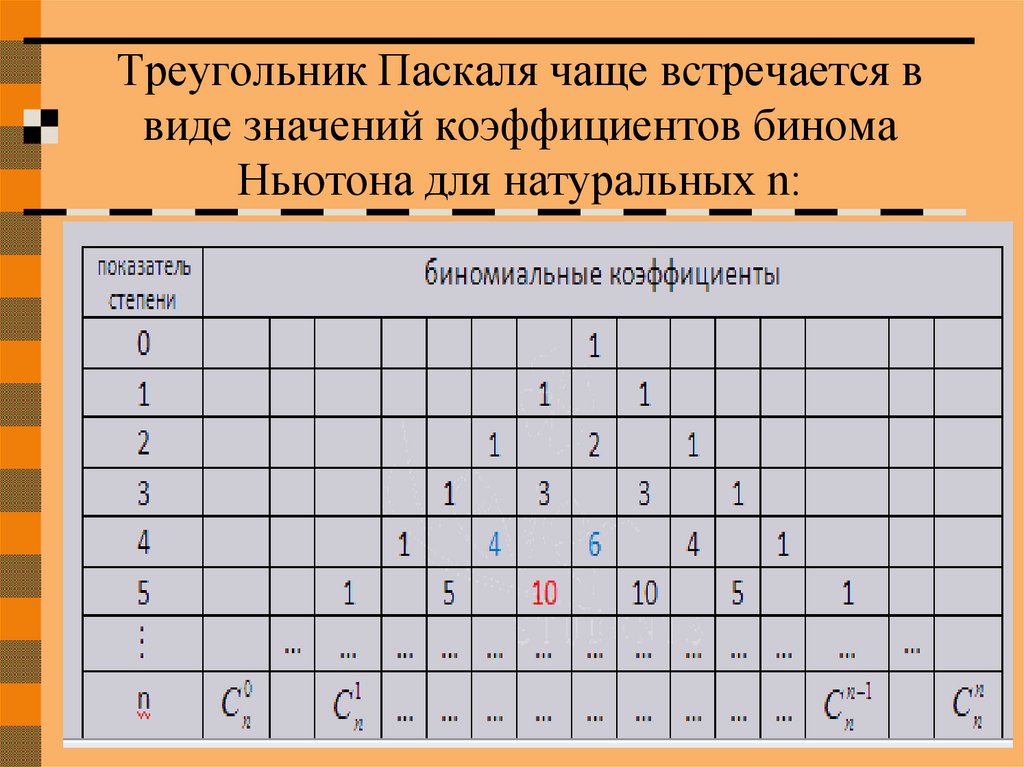
Треугольник Паскаля чаще встречается ввиде значений коэффициентов бинома
Ньютона для натуральных n:
11.
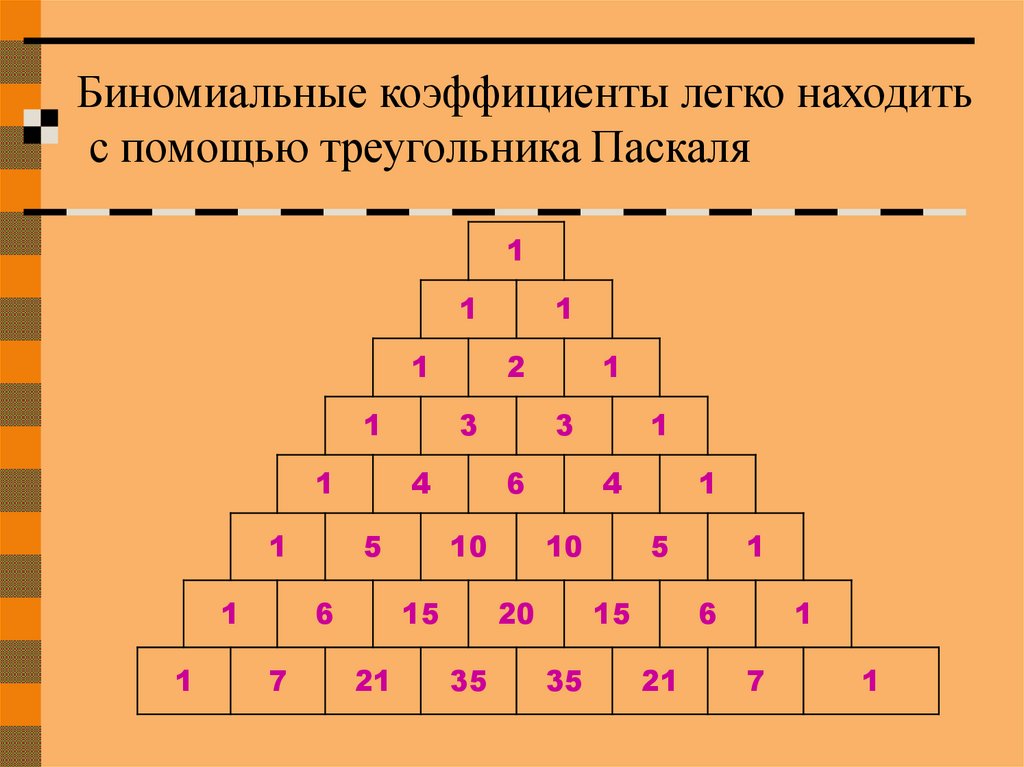
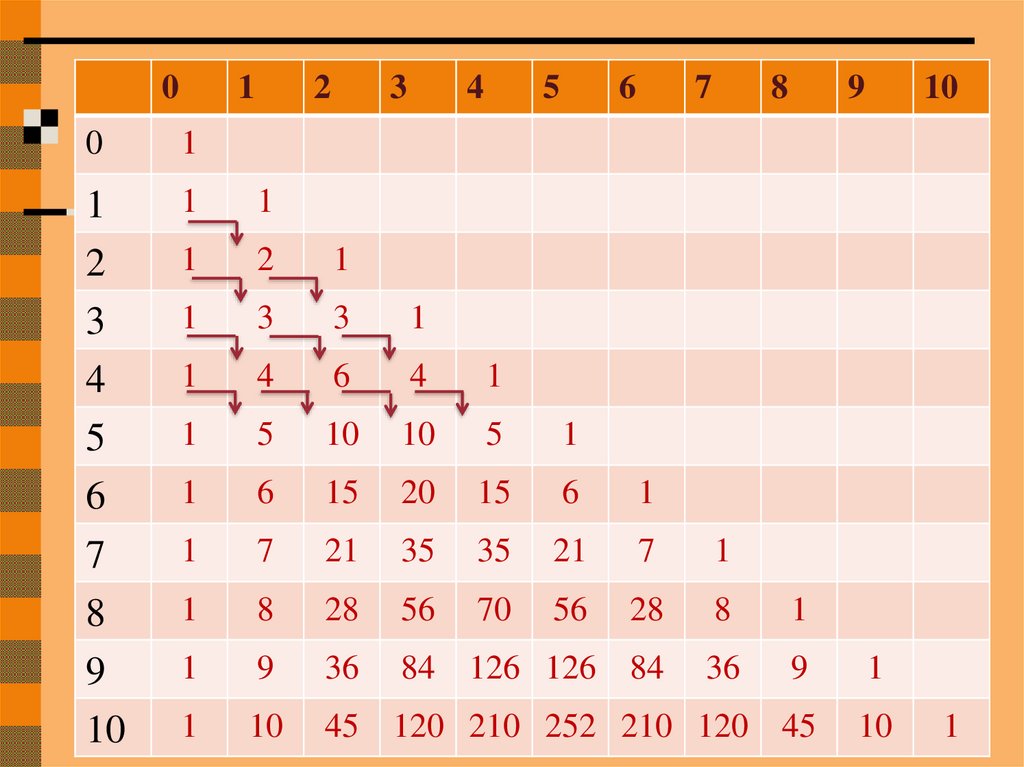
Боковые стороны треугольника Паскалясостоят из единиц. Внутри треугольника
Паскаля стоят числа, получающиеся
сложением двух соответствующих чисел над
ним. Например, значение десять (выделено
красным) получено как сумма четверки и
шестерки (выделены голубым). Это правило
справедливо для всех внутренних чисел,
составляющих треугольник Паскаля, и
объясняется свойствами коэффициентов
бинома Ньютона.
12.
Биномиальные коэффициенты легко находитьс помощью треугольника Паскаля
1
1
1
1
1
1
1
1
7
2
3
4
5
6
1
3
6
10
15
21
1
4
10
20
35
1
1
5
15
35
1
6
21
1
7
1
13.
1623-1662 г.г.ПАСКАЛЬ -французский
математик, физик,
религиозный философ и
писатель. Работы по
арифметике, теории
чисел, алгебре,
геометрии, теории
вероятностей. В 1641г.
сконструировал
суммирующую машину.
14.
01
2
3
4
5
6
7
8
9
10
0
1
1
2
3
4
5
6
7
8
9
10
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
1
9
36
84 126 126 84
36
9
1
1
10
45 120 210 252 210 120 45
10
1
15. Биноминальные коэффициенты:
m!С
n!( m n)!
O! 1
n
m
C
0
m
C
1
m
C
m
m
1
C
m 1
m
m
16. Биноминальные коэффициенты:
Сn
m 1
С
n
m 1
n 1
m
C
n 1
m 1
C
C
C
n
m
n
m
С C ... C
0
m
1
m
m 1
m
C 2
m
m
m
17.
Число слагаемых на 1 больше степенибинома.
Коэффициенты находятся по
треугольнику Паскаля.
Коэффициенты симметричны.
Если в скобке знак минус, то знаки + и –
чередуются.
Сумма степеней каждого слагаемого
равна степени бинома.






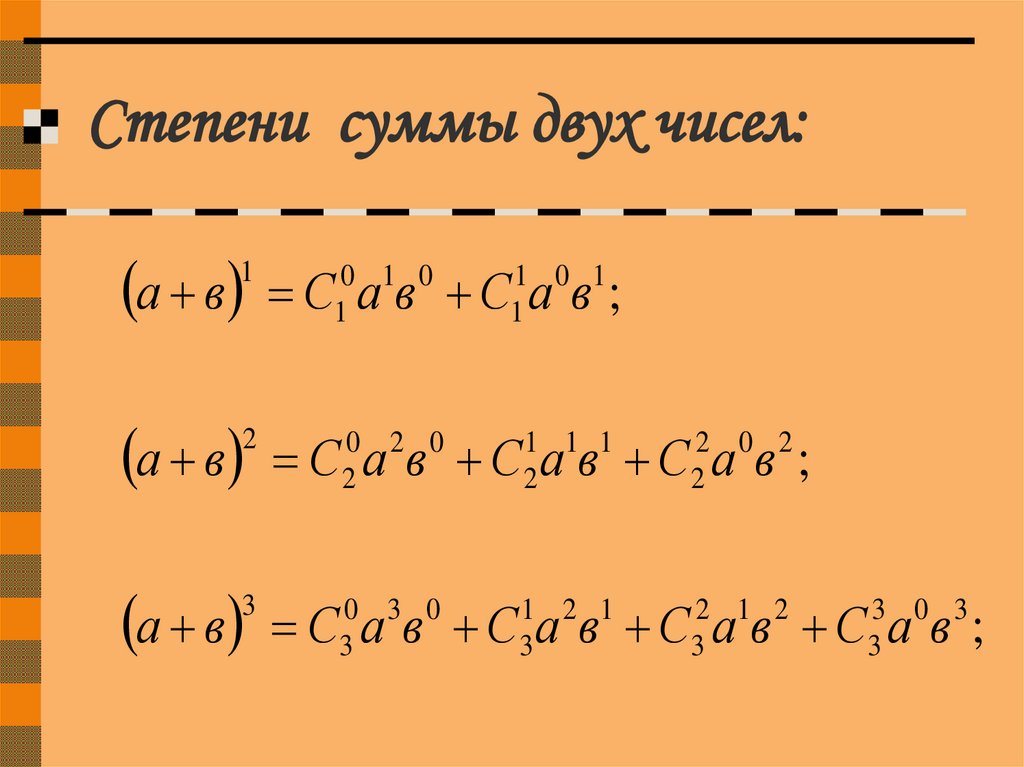



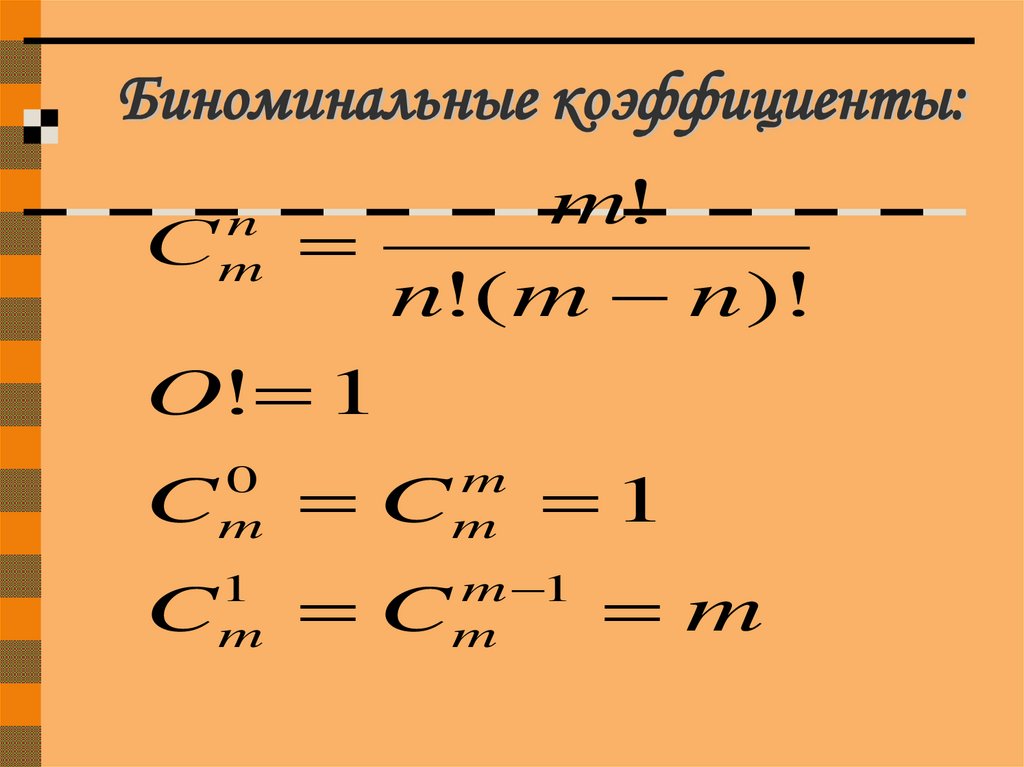


 Математика
Математика








