Кинематика плоского движения. (Продолжение)

1.

А.И. Родионов
Теоретическая механика.
Ч.1. КИНЕМАТИКА

2.

Лекция №7
Кинематика плоского движения. (Продолжение).
§7.1. Вычисление ускорений точек плоской фигуры.Теорема об ускорениях
точек плоской фигуры. (Теорема о сложении ускорений).
Получим выражение, для ускорения любой точки плоской фигуры, исходя
из формулы (41) и определения ускорения точки. Действительно,
d
VB V A VB / A
dt
d AB
dVB / A d
aB a A
a A AB a A AB
dt
dt
dt
VB / A d
aB a A
a A AB a A AB VB / A
dt
dt

3.

вр ц.с.
aB aA aB / A aA aB / A a B / A (45)
Таким образом,
ускорение любой точки В плоской фигуры геометрически
складывается из ускорения полюса А и ускорения точки В в её
вращении относительно А, которое состоит из вращательного и
центростремительного ускорений.
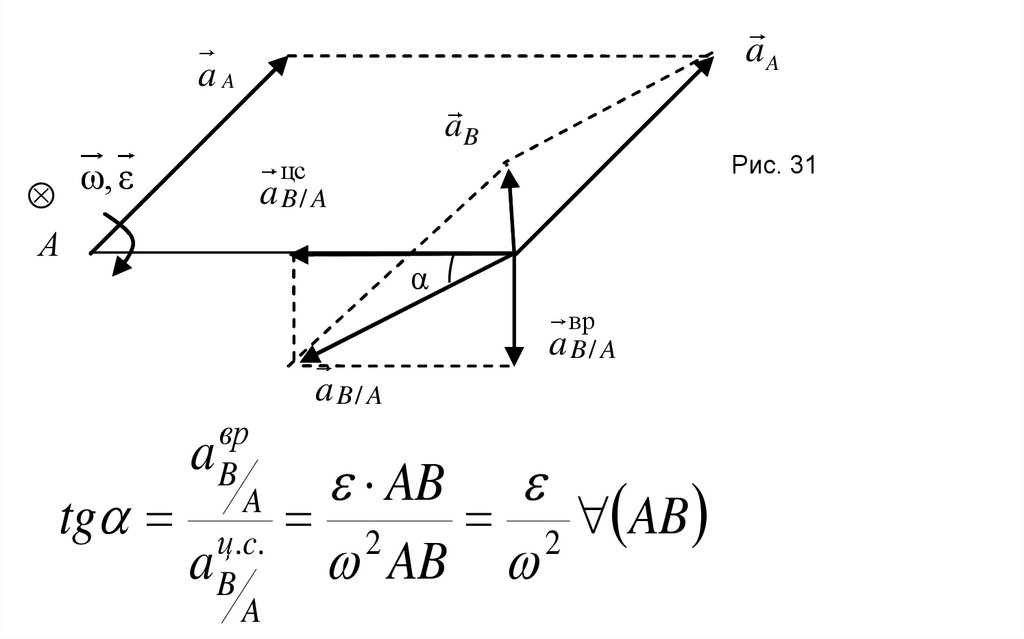
На рис.31. представлена геометрическая интерпретация формулы (45).

4.

aA
aA
aB
ω, ε
Рис. 31
цс
a B/ A
А
α
вр
a B/ A
a B/ A
tg
вр
aB
A
ц.c.
aB
A
AB
AB
2
2
AB

5.

2
2
вр
ц .c.
2
4
aB aB aB AB
A
A A
(46)
Заметим, что формула (45) остается справедливой и для
произвольного движения
твердого тела в силу своего вывода, если
ц .с.
о.с.
a
a
заменить в ней B / A на B / A .
§7.2. Примеры вычисления скоростей и ускорений точек
плоской фигуры.
§7.2.1. Вычисление скоростей точек.
Рассмотрим, в качестве примера, кривошипно–шатунный механизм с
колесом в точке С, представленный на Рис.30. Найдем сначала
скорости точек и, далее, ускорений.

6.

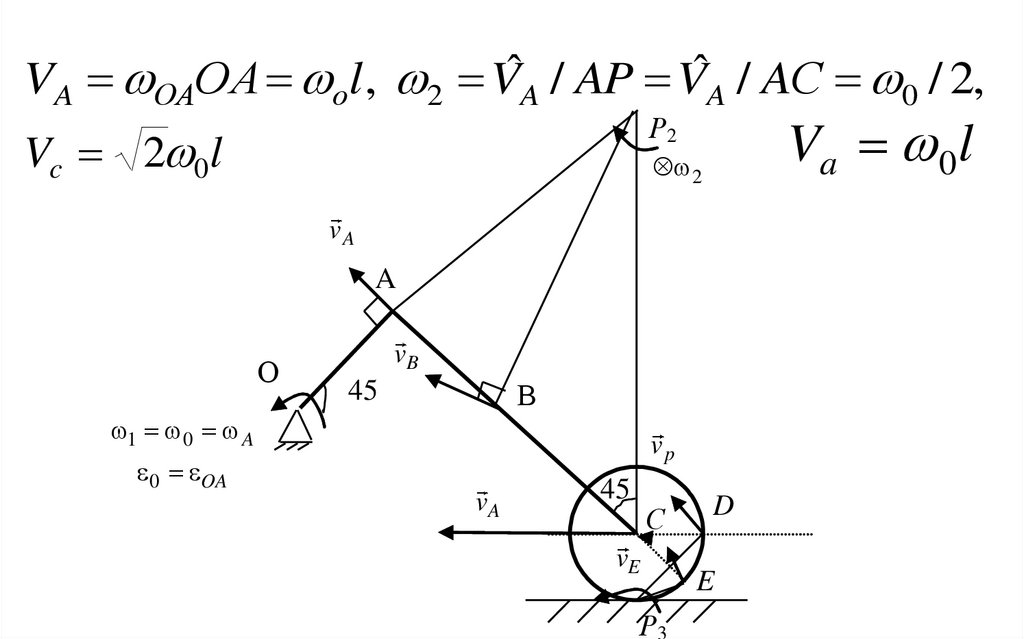
VA ОАОА оl , 2 VˆA / AP VˆA / AС 0 / 2,
Va 0l
Р2
Vc 2 0l
2
vA
A
О
vB
В
45
1 0 A
0 OA
vp
vA
45
С
vE
Р3
D
E

7.

§7.2.1. Вычисление ускорений точек плоской фигуры.
Рассмотрим вычисление ускорений точек. В соответствии с формулой (45)
d
VB V A VB
A
dt
d AB
d VB A d
aB a A
a A AB a A AB
dt
dt
dt
aB a A AB VB
A
n
A
цс
a B a A a B a A a вр
a
B
B
A
tg
вр
aB
A
цент
aB
A
a A a A a Axi a Ayj ...VB AB
A
A
AB
2 AB
2
AB

8.

2
2
вр
цент
2
4
a B a B a B AB
A
A A
ц .с .
вр .
a
a
Заметим, что так как ,
то это можно использовать для
определения aB / A ( ) . Заметим, что в случае, когда полное ускорение
точки известно по направлению, то при сложении векторов в (45)
разумно пользоваться правилом многоугольника. А там, где
направление ускорения не известно целесообразно пользоваться
правилом параллелограмма при сложении векторов в (45).
вр .
вр
aА
ц .с.
0l , a A
ц.с.
aС / А
2
ц .с.
0 l , aС / А 1 / 2
2
2 CA
2
0
4
2l
2
0
2
l
2
0l

9.

Далее воспользуемся методом проекций.
Суть метода проекций заключается в том, что вместо системы не
ортогональных векторов вводим заменяющую ее (эквивалентную ей)
систему ортогональных векторов, связанную с локальной декартовой
системой координат, через которую и определяется вектор и модуль
скорости точки.
Действительно
n
a Ax a Ay a A a A a Axi a Ayj
вр цс
вр
цс
aC а А аС / А (а А а А ) (аС / А аС / А ) а x а y а x ic а y jc
вр
вр
цс
а x а y а В ( а А а А ) (а В / А а Вцс/ А )
Заметим, что для определения ускорения точки В можно взять за
полюс как точку С, так и точку А. Допустим возьмем за полюс точку С.
Тогда
вр ц.с.
a A a0 a A a 0 a A a A
0
0
0

10.

вращ
X Aa a AX a0 cos 45 a A0
ц .с.
a
a
a
sin
45
a
YA AY
0
A
0
a 0в р
AP
вр ц.с.
a A a0 a A a0 a A a A
0
0
0
Заметим, что при качении одного тела по другому телу без
проскальзывания, то
вр
A
a
AP

11.

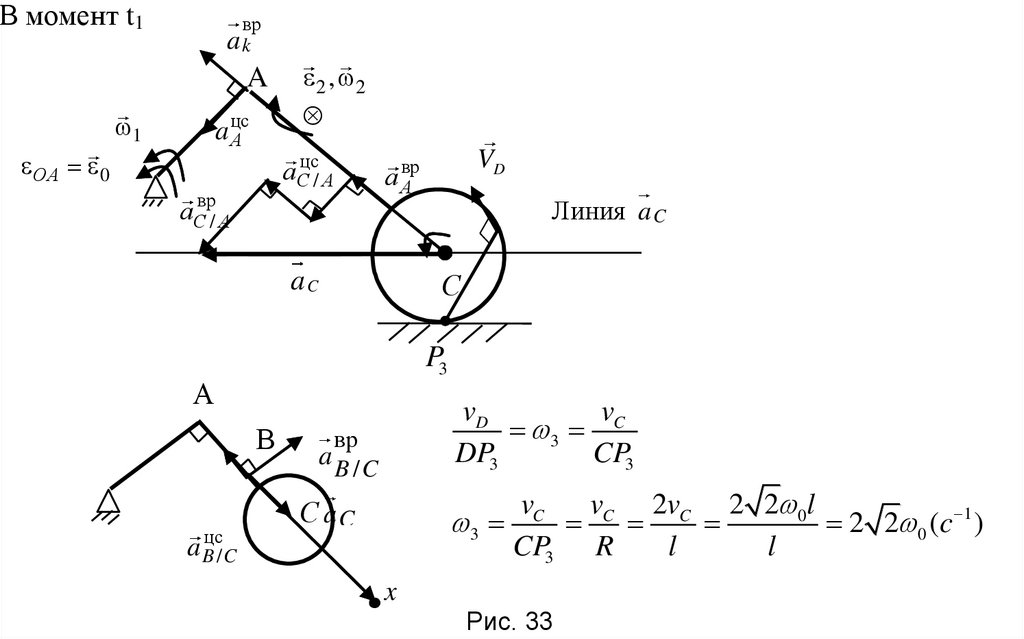
В момент t1
вр
ak
A
1
a цс
А
ОА 0
2 , 2
аСцс/ А
аСвр/ А
Линия a C
С
aC
P3
А
В
a Bцс/ C
VD
а Авр
vC
vD
3
DP3
CP3
вр
aB/C
С aC
3
vC
v
2v
2 2 0l
C C
2 2 0 (c 1 )
CP3 R
l
l
x
Рис. 33

12.

§7.3. Мгновенный центр ускорений.
Точка Q плоской фигуры или подвижной плоскости, в которой
лежит эта фигура, ускорение которой в данный момент времени
равно 0, называется мгновенным центром ускорений.
§7.3.1. Теорема о существовании МЦУ
Пусть ускорение полюса, например точки А, равно a A .
Тогда, если ,
0, 0 то МЦУ существует.
Отложим отрезок AQ под углом в направлении .
AQ
aA
2
4
arctg 2
(47)

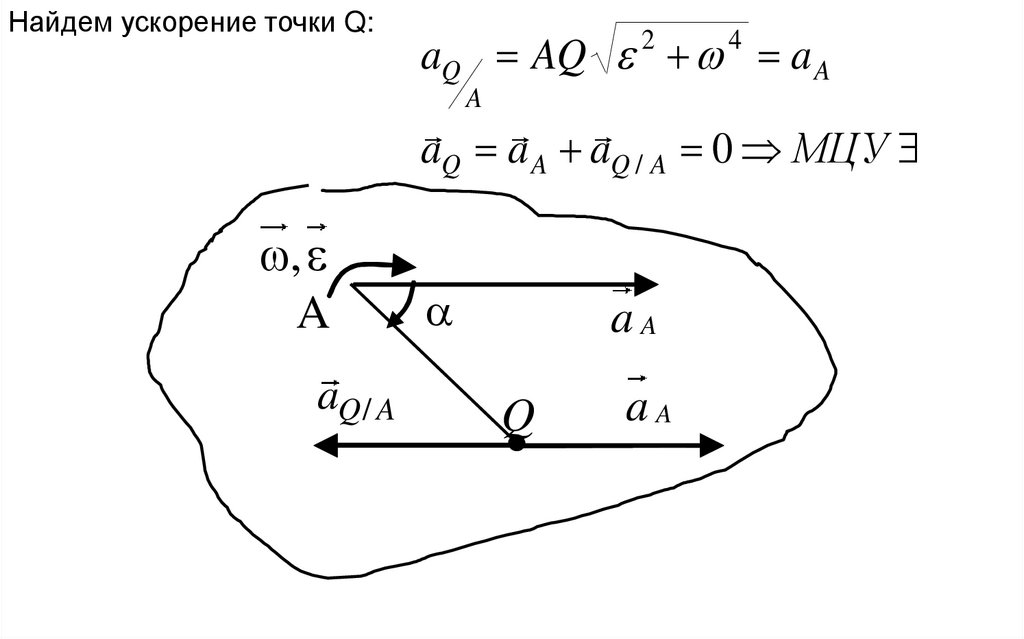
13.

Найдем ускорение точки Q:
aQ AQ a A
2
A
4
aQ a A aQ / A 0 МЦУ
,
A
aQ / A
aA
Q
aA

14.

Таким образом, МЦУ принадлежит отрезку, расположенному под углом
arctg 2
к вектору ускорения , который откладывается от ускорения полюса
aA
в сторону, соответствующую
“направлению вращения” , на расстояние
(от полюса) равное:
AQ
aA
2 4
На основании всего сказанного можно сконструировать “крестовую
формулу”, аналогичную такой же формуле для скоростей точек:
aA
AQ
2
aD
aB
4
DQ
BQ
aC
CQ
tg 2
(48)

15.

Модули ускорения точек плоской фигуры в каждый момент времени
пропорциональны расстояниям от этих точек до МЦУ, а вектор ускорений
составляет с отрезками, соединяющими эти точки с МЦУ, один и тот же
угол α.
§7.3.1. Способы определения МЦУ.
1
1) Известна точка плоской фигуры, ускорение которой в данный момент
равно нулю.
aC 0 C Q В
aP
vC
C
Q
Р
Рис. 35

16.

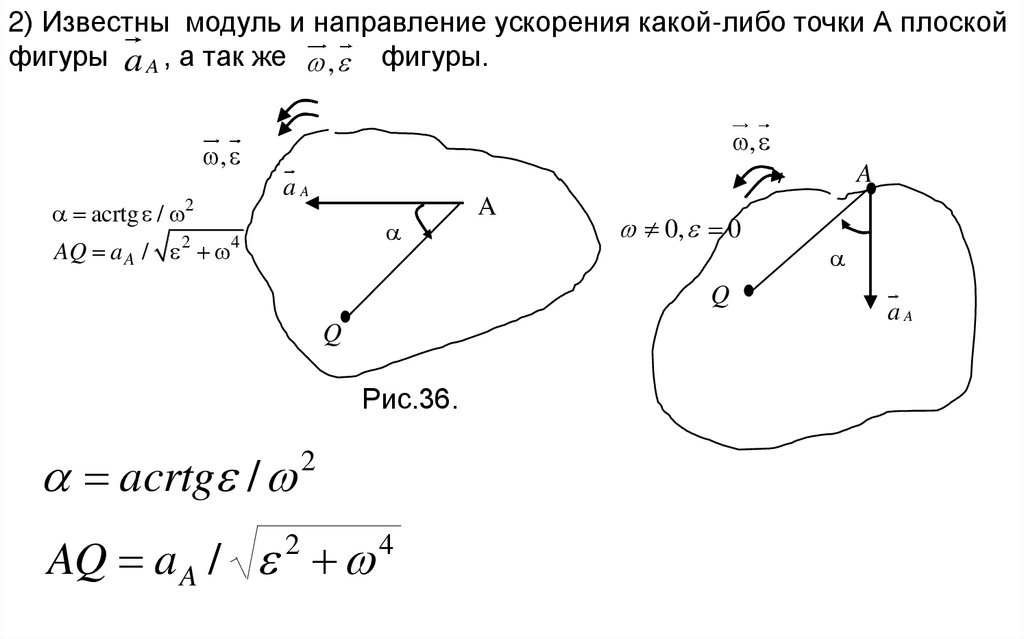
2) Известны модуль и направление ускорения какой-либо точки А плоской
фигуры a A , а так же , фигуры.
,
,
A
aA
acrtg / 2
AQ a A /
2
4
A
0, 0
Q
Q
Рис.36.
acrtg /
2
AQ a A / 2 4
aA

17.

2.
А
aA
Q
tg / 2 0
и
0
Рис. 37

18.

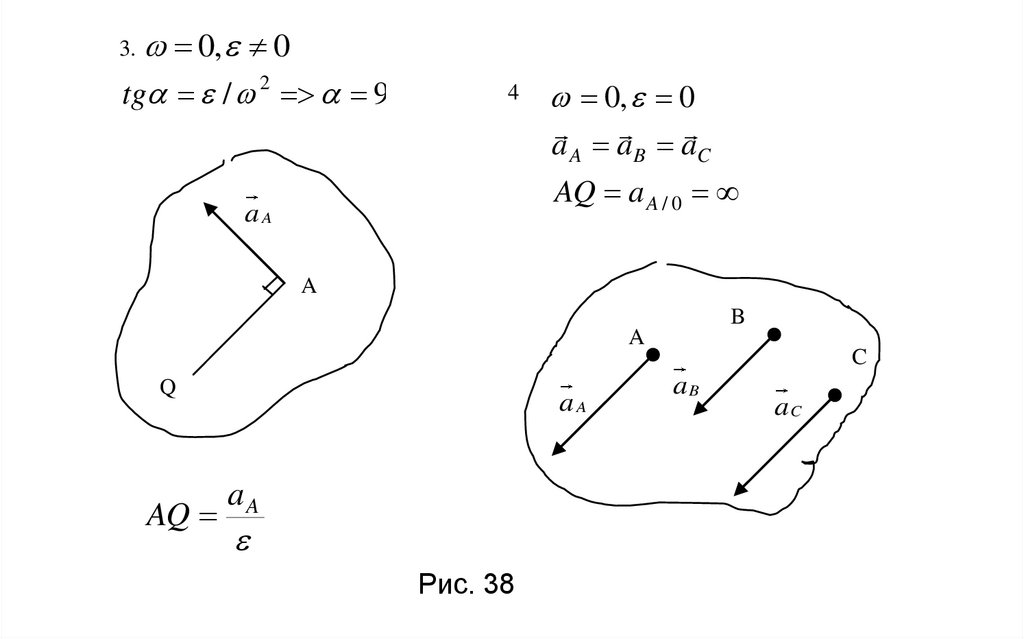
3. 0, 0
tg / 2 90
4
0, 0
a A aB aC
AQ a A / 0
aA
A
B
A
Q
AQ
aA
aA
Рис. 38
C
aB
aC

19.

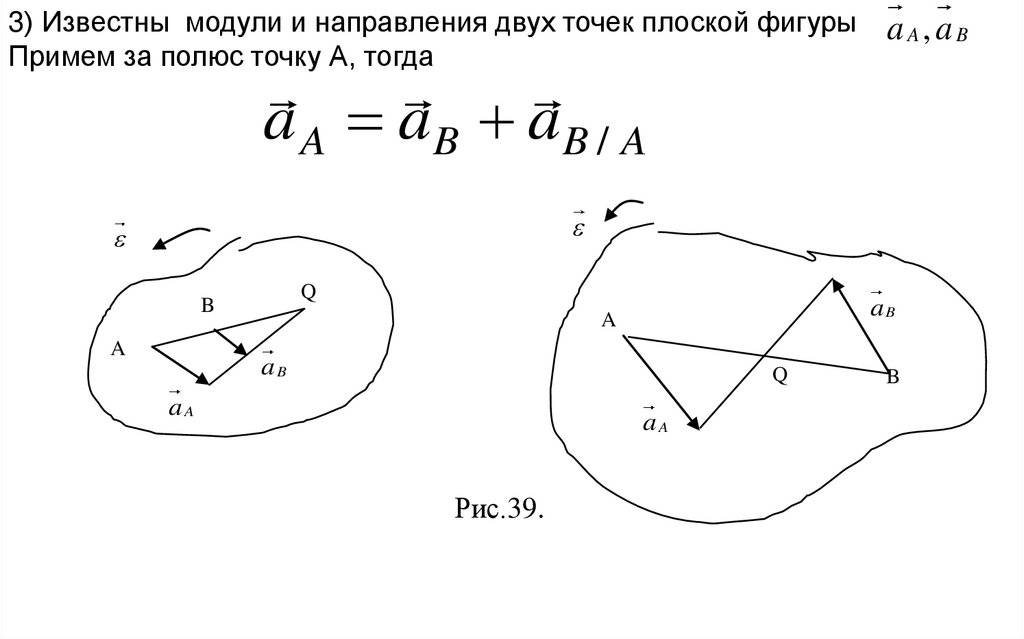
3) Известны модули и направления двух
1 точек плоской фигуры
Примем за полюс точку А, тогда
aA, aB
a A aB aB / A
Q
B
A
aB
A
aB
Q
aA
aA
Рис.39.
B