Основы алгебры логики

1.

ОСНОВЫ АЛГЕБРЫ
ЛОГИКИ

2.

В вычислительной технике происходит преобразование информации,
представленной в виде двоичных кодовых комбинаций. В отдельных
частях ЭВМ используются устройства, преобразующие одну комбинацию
(входную) в другую (выходную). Преобразование происходит в момент
поступления входной комбинации (с некоторой задержкой по времени,
которая не существенна) и не зависит от тех комбинаций, которые
поступали в предшествующие моменты времени. Такие устройства
принято называть комбинационными. Поскольку преобразование
происходит
автоматически,
то
иногда
используется
термин
«комбинационный автомат».
Любая логическая функция может быть представлена в виде словесного
описания.

3.

• Например,
логическая функция Пирса (стрелка Пирса) словесно
может быть описана так: значение функции Пирса равно 1 только
тогда, когда обе входные переменные и х2 равны нулю, при любых
других значениях входных переменных значение функции Пирса
равно 0.
• Эту же функцию можно представить в табличной форме — в виде
таблицы истинности или карты Карно.
• Таблица истинности и карта Карно содержат все четыре возможных
входных набора и значения функции, соответствующие каждому из
них.

4.

Карта Карно для логической функции двух переменных:
Карта Карно для логической
функции трех переменных
Карта Карно для логической
функции четырех переменных

5.

Базис алгебры логики
Любая логическая функция может быть записана с помощью трех элементарных
функций: инверсии (НЕ), дизъюнкции (ИЛИ), конъюнкции (И). Проведя
преобразования записанной таким образом формулы, можно ее упростить, т.е.
уменьшить число выполняемых при расчете операций. Однако такие преобразования в
целях упрощения сами по себе не так уж просты, для их выполнения требуется опыт,
надо ими часто заниматься. Поэтому порой при расчете вручную можно просто
последовательно подставлять все возможные наборы переменных и определять для
них значение функции. Это не очень сильно удлинит расчет. Но в вычислительной
технике значения логической функции определяет не человек, а комбинационное
устройство. Чтобы это устройство состояло из меньшего числа элементов, а сами
элементы были в максимальной степени однотипными, необходимо преобразовать
реализуемую логическую функцию в определенную форму. В алгебре логики
различают несколько форм, которым соответствуют наиболее рациональные
построения схем комбинационных устройств.

6.

• Логические функции, представляющие собой дизъюнкции отдельных членов,
каждый из которых, в свою очередь, есть некоторая функция, содержащая
только конъюнкции и инверсии, называются логическими функциями
дизъюнктивной формы. Форма представления дизъюнктивной функции, в
которой инверсия применяется лишь непосредственно к аргументам, но не к
более сложным функциям этих аргументов, называется дизъюнктивной нормальной формой (ДНФ) представления функций. Если же каждый член ДНФ
от п аргументов содержит все эти л аргументов (с инверсией или без нее), то
такая форма представления функции называется совершенной дизъюнктивной
нормальной формой (СДНФ).
• Логические функции, представляющие собой конъюнкцию отдельных членов,
каждый из которых есть функция, содержащая только дизъюнкции и инверсии,
называются логическими функциями конъюнктивной формы. По аналогии с
дизъюнктивными формами возможны конъюнктивные нормальные формы
(КНФ) и совершенные конъюнктивные нормальные формы (СКНФ).

7.

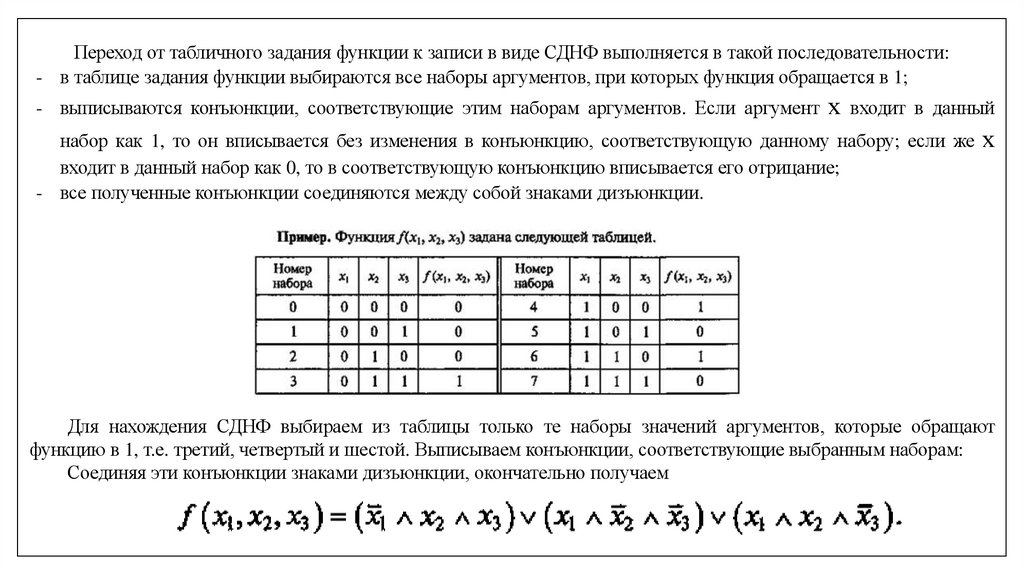
Переход от табличного задания функции к записи в виде СДНФ выполняется в такой последовательности:
- в таблице задания функции выбираются все наборы аргументов, при которых функция обращается в 1;
- выписываются конъюнкции, соответствующие этим наборам аргументов. Если аргумент х входит в данный
набор как 1, то он вписывается без изменения в конъюнкцию, соответствующую данному набору; если же х
входит в данный набор как 0, то в соответствующую конъюнкцию вписывается его отрицание;
- все полученные конъюнкции соединяются между собой знаками дизъюнкции.
Для нахождения СДНФ выбираем из таблицы только те наборы значений аргументов, которые обращают
функцию в 1, т.е. третий, четвертый и шестой. Выписываем конъюнкции, соответствующие выбранным наборам:
Соединяя эти конъюнкции знаками дизъюнкции, окончательно получаем

8.

Аналогично выполняется переход от табличного задания функции к записи в виде СКИФ:
- в таблице задания функции выбираются все наборы аргументов, при которых функция обращается в 0;
- выписываются дизъюнкции, соответствующие этим наборам аргументов. Если аргумент х входит в данный
набор как 0, он вписывается без изменения в дизъюнкцию, соответствующую данному набору; если же х входит в
данный набор как 1, то в соответствующую дизъюнкцию вписывается его отрицание;
- все полученные дизъюнкции соединяются между собой знаками конъюнкции.
Выбор той или иной формы аналитической записи определяется видом таблицы заданной функции. Если
большинство значений данной функции 0, то выгодно записывать ее в СДНФ, в противном случае более экономную
запись дает СКНФ.

9.

Минимизация логических функций
• В ряде случаев запись в СДНФ или СКНФ не является самой простой для выражения
заданной функции в аналитической форме и можно упростить логическое
выражение, не нарушая значения функции. Методы такого упрощения называются
методами минимизации. В результате минимизации логические функции могут быть
представлены в ДНФ или КНФ с минимальным числом членов и минимальным
числом аргументов в каждом члене. Для упрощения выражений функций алгебры
логики разработаны как графические, так и алгебраические методы.
• Из
большого числа различных приемов и методов минимизации логических
функций рассмотрим только один. При небольшом числе переменных удобен
графический метод упрощения выражений для функций алгебры логики с помощью
карт Карно.

10.

При записи функции в минимальной форме по карте Карно используют
следующие правила.
• Все клетки, содержащие 1, объединяют в замкнутые области.
• При этом каждая область должна представлять собой прямоугольник с числом
клеток 2К, где к = 0, 1, 2, 3, ... Области могут пересекаться, т. е. одни и те же
клетки могут входить в разные области.
• Затем производят запись минимального выражения в дизъюнктивной
нормальной форме (МДНФ). Каждая область в такой записи представляется
членом, число аргументов в котором на к меньше общего числа аргументов
функции л, т. е. равно л - к. Каждый член МДНФ составляется лишь из тех
аргументов, которые для соответствующей области имеют значения либо без
инверсий, либо только с инверсией.
Таким образом, при охвате клеток замкнутыми областями следует стремиться,
чтобы число областей было минимальным (так как при этом будет минимальным
число членов в МДНФ), а каждая область содержала возможно большее число
клеток, поскольку при этом число аргументов в членах будет минимальным.

11.

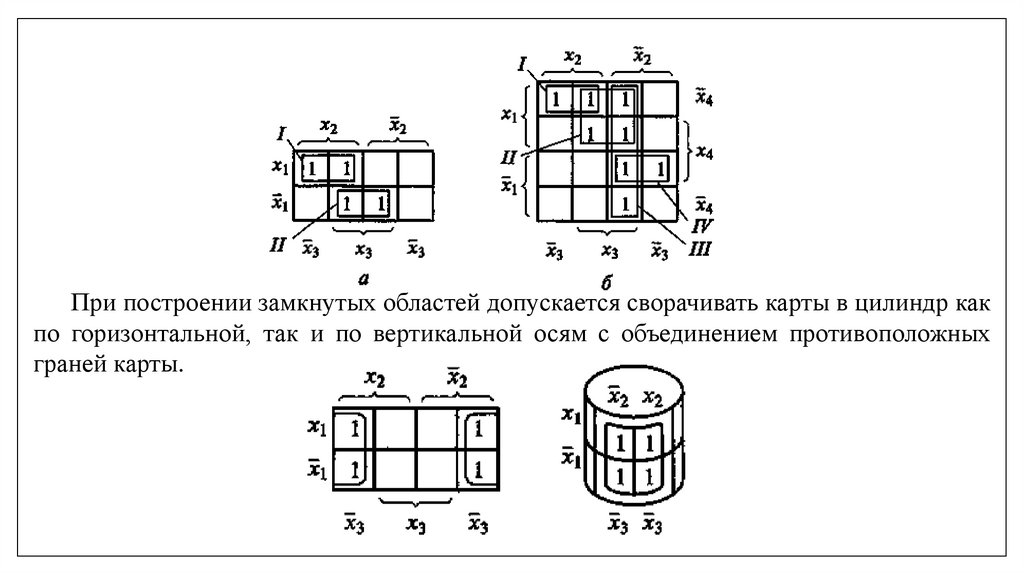
При построении замкнутых областей допускается сворачивать карты в цилиндр как
по горизонтальной, так и по вертикальной осям с объединением противоположных
граней карты.