Биномиальное распределение

1. Биномиальное распределение

Муравьева Анастасия 142

2. Разберём понятие

Где вы слышали слово биномиальный? С каким
опредеднием это слово связно?
Бином Ньютона - это формула, которая помогает возвести
сумму двух чисел в любую степень.
- Биномиальный коэффициент

3. Определение

Биномиальное распределение используется для
моделирования ситуаций, где проводится фиксированное
количество независимых испытаний, каждое из которых
имеет два возможных исхода: успех или неудача.
Приведите пример таких испытаний.
• Подбрасывание монеты (орёл или решка).
• Сдача экзаменов (сдал или не сдал).
• Контроль качества (изделие годное или бракованное).

4. Формула

Если проводится n независимых испытаний, то вероятность
того, что успех произойдёт ровно m раз, вычисляется по
формуле:
— число сочетаний из n по m (количество способов
выбрать m успехов из nn испытаний),
pm — вероятность m успехов,
qn−m — вероятность n−m неудач.

5.

С помощью какой формулы можно определить
биномиальное распределение?
Распределение вероятностей, определяемое формулой
Бернулли, называется биномиальным

6. Свойства биномиального распределения

7.

Составьте закон распределения числа выпадений герба
(орла) при трёх бросаниях монеты.
Решение:
• Число испытаний (n): 3 (так как монета бросается 3 раза).
• Вероятность успеха (p): 0,5 (вероятность выпадения герба
при одном бросании).
• Случайная величина (m): число выпадений герба (может
принимать значения от 0 до 3).

8.

9.

Сумма всех вероятностей должна быть равна 1:
0,125+0,375+0,375+0,125=1.
m
P(m)
0
1,125
1
0,375
2
0,375
3
0,125
Распределение симметрично, так как p=0.5. Наибольшая
вероятность соответствует m=1 и m=2, а вероятности
уменьшаются при удалении от этих значений.

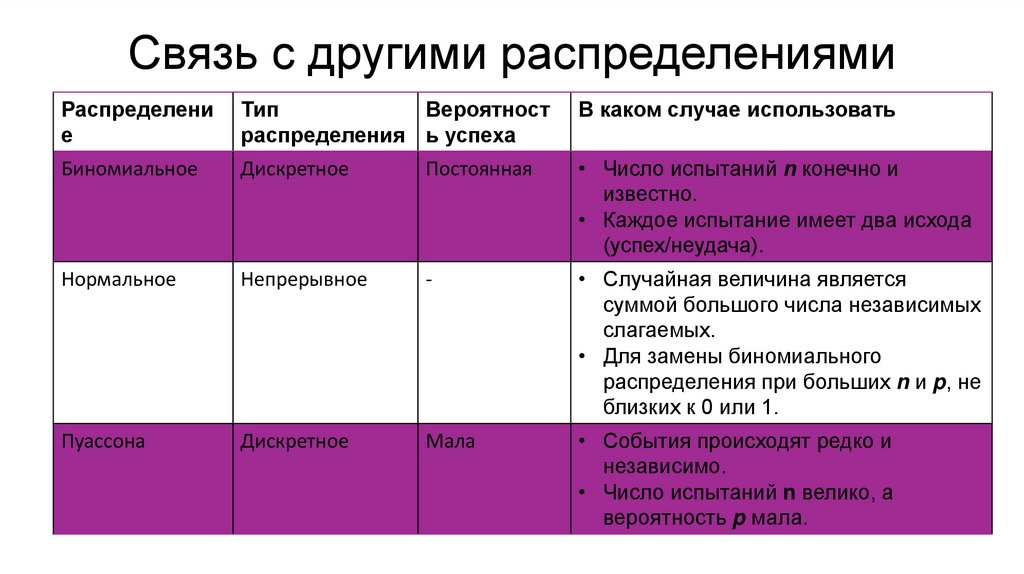
10. Связь с другими распределениями

Распределени
е
Тип
Вероятност
распределения ь успеха
В каком случае использовать
Биномиальное
Дискретное
Постоянная
• Число испытаний n конечно и
известно.
• Каждое испытание имеет два исхода
(успех/неудача).
Нормальное
Непрерывное
-
• Случайная величина является
суммой большого числа независимых
слагаемых.
• Для замены биномиального
распределения при больших n и p, не
близких к 0 или 1.
Пуассона
Дискретное
Мала
• События происходят редко и
независимо.
• Число испытаний n велико, а
вероятность p мала.

11. Пример

Летняя сессия студента Гены Зубрилова выдалась очень
жаркой (до +30oC ) и длинной (пять экзаменов), так что
подготовить он сумел только 3/4 билетов по каждому
предмету. Какова вероятность, что его отчислят сразу после
сессии и даже не допустят к пересдаче?

12.

По правилам деканата отчисление производится сразу после
сессии, если студент не сумел сдать с первого раза больше одного
предмета.
Будем считать, что каждый экзамен есть испытание в схеме
Бернулли с вероятностью успеха (сдачи) p = 3/4 . В такой
постановке перед нами стоит задача отыскания для случайного
числа ξ вероятности P{ξ≤3}.
Заметим, что противоположное событие {ξ > 4} содержит меньше
элементов, поэтому лучше найти вероятность этого события, а
затем воспользоваться формулой для вероятности
дополнительного события.

13.

Используем формулу биномиального распределения для
каждого случая:
P{ξ≥4}=P{ξ=4}+P{ξ=5}

14.

Суммируем вероятности
Теперь находим вероятность отчисления

15. Вопросы для самопроверки

• Как изменится биномиальное распределение,
если p увеличить?
• Почему при больших n биномиальное распределение
приближается к нормальному?
• Приведите пример задачи, где биномиальное
распределение неприменимо.