Лекция 12 ВМ1_АПТ

1.

Лекция 12
Переменная Бернулли. Равномерное
распределение.Биномиальное распределение.
Серимбетов М.А.

2. План лекции

1. Переменная Бернулли
2. Равномерное распределение
3. Биномиальное распределение.
4. Математическое ожидание и дисперсия СВ,
распределенной по закону Бернулли.
5. Биномиальное распределение.
6. Закон больших чисел.
7. Примеры
Аскарова А.Ж.

3.

Детерминированный закон распределения
Определение X является
детерминированной переменной со
значением a, если X a , и тогда
P X a 1.
Утверждение 1 если X - детерминированная
переменная со значением a , тогда E X a
и V X 0.
Аскарова А.Ж.

4.

Равномерный закон распределения
Определение Пусть n N . Закон X
называется равномерным на {1, ...,n}, если
X 1,..., n , и k 1,..., n , P X k 1 .
n
Обозначение: X U
1,..., n
Аскарова А.Ж.

5.

Равномерный закон распределения
Пример 1.
1. Выбираем наугад объект среди n объектов,
отмеченных от 1 до n. X - номер выбранного
объекта. X U 1,..., n
2. Мы бросаем правильную игральную
кость. X - это цифра, которую мы получаем:
X U 1,...,6 .
Аскарова А.Ж.

6.

Равномерный закон распределения
Утверждение 2.
Если
n 1
.
X U 1,..., n , то E X
2
Доказательство :
1 n
n n 1 n 1
E X kP X k k
.
n k 1
2n
2
k 1
n
Аскарова А.Ж.

7.

Закон Бернулли
В схеме Бернулли рассматривается серия,
состоящая из n независимых испытаний,
каждое из которых имеет лишь две
исхода:
1. наступление какого-то события A
(успех)
2. или его не наступление Ā (неудача).
Причем вероятность успеха при одном
испытании P(A)= p – постоянна
и не зависит от номера испытания.
Следовательно, вероятность неуспеха
P(Ā)= 1-p = q тоже постоянна.
Якоб Бернулли
1654-1705
Швейцарский
математик
Аскарова А.Ж.

8.

Закон Бернулли
Определение Пусть Х является переменной
Бернулли с параметром р р 0,1 , если
X 0,1 , и Р Х 1 р, P X 0 1 р q.
Обозначение:
X B p .
https://www.coursera.org/lecture/theory-of-chances/42-skhiema-ispytanii-biernulli-F68OE
Аскарова А.Ж.

9.

Закон Бернулли
Пусть дано событие А, пусть Х=1, если А
произойдет, и Х=0, если иначе. Тогда X B p .
X B Р А .
Утверждение 3 Если X В р , то E X р
и V X pq.
Доказательство. E Х 1 Р Х 1 0 Р Х 0 р.
Х 2 Х , тогда V Х E Х 2 Е Х 2 р р 2 pq.
Аскарова А.Ж.

10.

Биномиальное распределение
Пусть производится п независимых
испытаний, в каждом из которых событие А
может появиться либо не появиться.
Вероятность наступления события во всех
испытаниях постоянна и равна р
(следовательно, вероятность непоявления
q=1—р).
Рассмотрим в качестве дискретной случайной
величины X число появлений события А в
этих испытаниях.
Аскарова А.Ж.

11.

Биномиальное распределение
Найдем закон распределения величины X.
Для ее решения требуется определить
возможные значения X и их вероятности.
Очевидно, событие А в п испытаниях может
либо не появиться, либо появиться 1 раз,
либо 2 раза, ..., либо п раз.
Таким образом, возможные значения X
таковы: х1 = 0, x2=1, х3= 2, ..., хп+1 = п.
По формуле Бернулли: Pn(k)= C nk p k q n k
где k = 0, 1, 2, .... п.
Аскарова А.Ж.

12.

Биномиальное распределение
Определение Пусть Х является
биномиальной переменной с параметрами n
и р n N , р 0,1 , если X 0,..., n , и
для всех
q 1 p .
n k n k
k 0,..., n , Р Х k p q , при
k
Обозначение
X B n, p .
Аскарова А.Ж.

13.

Биномиальное распределение
Проводится n независимых экспериментов
Бернулли с вероятностью успеха p, X - число
успехов, тогда X B n, p .
X 0,..., n , и для всех k 0,..., n , каждая
последовательность с k успехами и n-k неудачами
происходит с вероятностью p
k
q
n k
, существует
n
случаев с k успехами и n-k неудачами (мы
k
должны выбрать место успеха в последовательности
результатов). Поэтому Р Х k n p k q n k
k
Аскарова А.Ж.

14.

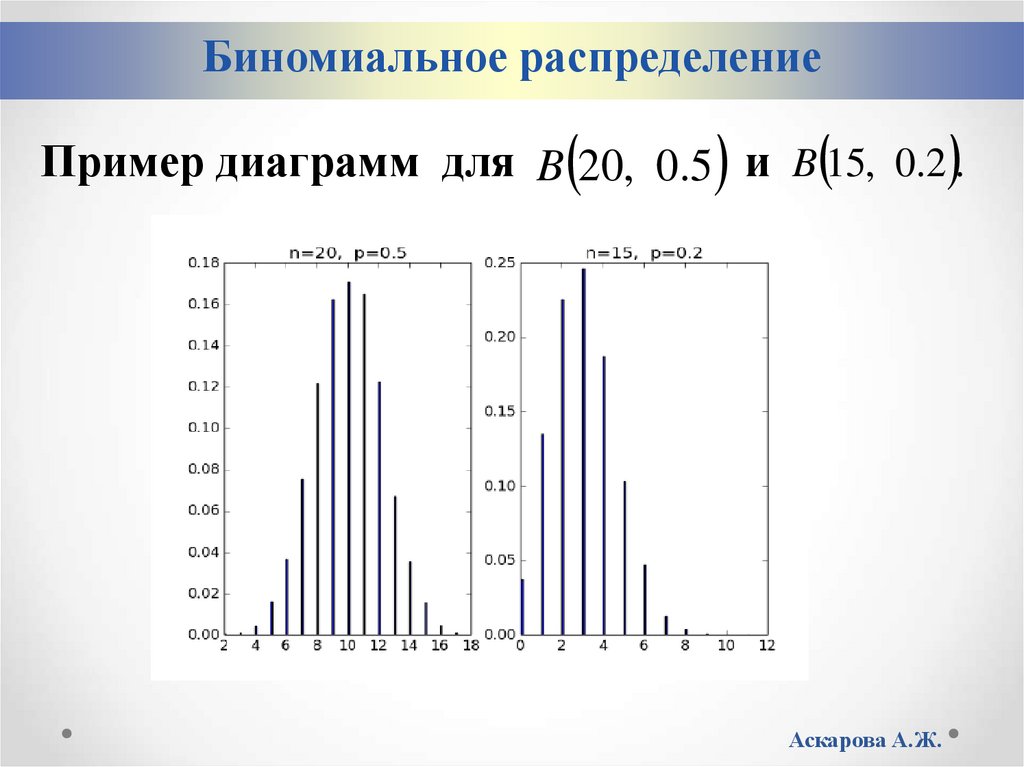
Биномиальное распределение
Пример диаграмм для B 20, 0.5 и B 15, 0.2 .
Аскарова А.Ж.

15.

Биномиальное распределение
Биномиальным называют распределение
вероятностей, определяемое формулой
Бернулли.
Закон назван «биномиальным» потому,
k
k n k
C
p
что правую часть равенства Pn(k)= n q
можно рассматривать как общий член
разложения бинома Ньютона:
(p + q)n = С nn pn+С nn 1 pn-1q +… +С nk pkqn-k+…+ С n0 qn
Аскарова А.Ж.

16.

Биномиальное распределение
Таким образом, первый член
разложения рп определяет вероятность
наступления рассматриваемого события п
раз в п независимых испытаниях; второй
член npn-1q определяет вероятность
наступления события п—1 раз; . . .;
последний член qn определяет вероятность
того, что событие не появится ни разу.
Аскарова А.Ж.

17.

Биномиальное распределение
Утверждение 4. Если X B n, p , то E X nр
и V X npq.
Доказательство.
n
n k n k
n k n k
E Х k p q k p q
, k 1,..., n ,
k 0
k 1
k
k
n
n
n 1
n!
n 1 !
.
k k
n
n
k 1 ! n 1 k 1 !
k! n k !
k
k 1
n 1 n 1
n 1 k 1 n 1 k 1
i n 1 i
n 1
p q
p q
E Х np
np
np p q np ,
k 1 k 1
i 0 i
n
Аскарова А.Ж.

18.

Биномиальное распределение
n
n k n k
n 1 k 1 n 1 k 1
p q
E Х X 1 k k 1 p q np k 1
,
k 1
k 1
k
k 1
n
n 1 i n 1 i
p q
E Х X 1 np i
np n 1 p ,
i 0 i
n 1
(используя результат для E(X) и заменив n на
n-1 ) получим
V X Е Х Х 1 Е Х Е Х
2
n n 1 р 2 nр n 2 р 2 n р р 2 npq.
Аскарова А.Ж.

19.

Биномиальное распределение
Другой способ доказательства.
Мы проводим n независимых экспериментов Бернулли с
вероятностью успеха p. Пусть X i 1 , если мы
получаем успех во время эксперимента номер i , X i 0
иначе. X i B p .
n
Пусть X X i, тогда X -n общее число
успехов, и X B n, p .
n
i 1
Мы видим, что E X E X i p np.
i 1
i 1
n
Позже мы увидим, что V X V X i , поскольку X i
i 1
независимы.
Таким образом, V X npq.
Аскарова А.Ж.

20.

Биномиальное распределение
Определение Пусть X и Y случайные величины на
( , P , P ). Мы говорим, что X и Y независимы,
если
x, y X Y ,
P X x Y y P X x P Y y .
Аскарова А.Ж.

21.

Биномиальное распределение
Определение Пусть X и Y случайные величины на
( , P , P ). Мы говорим, что X и Y независимы,
если
x, y X Y ,
P X x Y y P X x P Y y .
Утверждение 5 Пусть X и Y независимые случайные
величины такие, что X B n, p и Y B m, p , тогда,
X Y B n m, p .
Аскарова А.Ж.

22.

Биномиальное распределение
Пусть n+m независимых экспериментов Бернулли с
вероятностью успеха p
Пусть X - число успехов во время n первых
экспериментов, а Y - число успехов во время
последних m экспериментов.
X B n, p и Y B m, p , и X и Y независимы, так
как эксперименты независимы.
X+Y - это число успехов во время n+m
экспериментов, поэтому
X Y B n m, p .
Аскарова А.Ж.

23.

Закон больших чисел
Под
законом
больших
чисел
в
узком
смысле
понимается ряд математических теорем, в каждой из
которых при соблюдении определенных условий
устанавливается
факт
характеристик
большого
приближения
числа
средних
испытаний
некоторым определенным постоянным.
Аскарова А.Ж.
к

24.

Закон больших чисел
Различные формы закона больших чисел вместе с
различными
формами
центральной
предельной
теоремы образуют совокупность так называемых
предельных теорем теории вероятностей.
Предельные теоремы дают возможность не только
осуществить научные прогнозы в области случайных
явлений, но и оценивать точность этих прогнозов.
Аскарова А.Ж.

25.

Закон больших чисел
Закон больших чисел – это совокупность теорем и
связанных с ними неравенств, дающих ответ на
следующие важные вопросы:
– каким должно быть число испытаний для
обеспечения заданной точности;
– каковы границы возможного разброса значений
СВ при заданном числе испытаний и заданной
надежности;
– с какой вероятностью (надежностью) можно
доверять результатам, полученным при известном
числе испытаний и заданной
величине разброса
СВ?
Аскарова А.Ж.

26.

Закон больших чисел
Суть Закона больших чисел заключается в
следующем: при большом числе СВ Хi с
вероятностью, близкой к 1, можно утверждать, что
абсолютная величина разности между средней
арифметической этих СВ и константой – средней
арифметической их математических ожиданий M(Xi)
сколь угодно мала.
Отсюда следует, что при большом числе испытаний с
большой вероятностью средние характеристики СВ
стремятся к постоянным неслучайным величинам.
Аскарова А.Ж.

27.

Закон больших чисел
Закон больших чисел включает:
1) Неравенство Бьенеме - Чебышёва;
2) Лемму Маркова;
3) Обобщенную теорему Чебышёва;
4) Следствия из обобщенной теоремы Чебышёва:
а) Теорему Бернулли;
б) Теорему Пуассона;
5) Закон больших чисел ( теорему Чебышёва).
Аскарова А.Ж.

28.

Закон больших чисел
Андрей Андреевич Марков
(1856 —1922) — русский математик,
академик, внёсший большой вклад в
теорию вероятностей, математический
анализ и теорию чисел.
Утверждение 6. (неравенство Маркова) Пусть X -
положительная случайная величина : a 0,
E X
P X a
.
a
Аскарова А.Ж.

29.

Закон больших чисел
Доказательство:
E X
xP X x xP X x xP X x ,
x X , x a
x X , x a
x X , x a
поскольку X положителен
E X
aP X x a P X x aP X a .
x X , x a
x X , x a
Аскарова А.Ж.

30.

Закон больших чисел
Неравенство Маркова дает вероятностную оценку
того, что значение неотрицательной случайной
величины превзойдет некоторую константу через
известное математическое ожидание.
Когда никаких других данных о распределении нет,
неравенство дает некоторую информацию, хотя
зачастую оценка груба или тривиальна.
Аскарова А.Ж.

31.

Пример 2
Среднее число вызовов наладчика станков за смену равно
21. Оценить вероятность того, что за смену поступит
вызовов:
- не менее 60;
- менее 35.
Число вызовов – положительная случайная величина Х с
М[X] = 21.
В соответствии с леммой Маркова для первого случая t = 60:
P( X 60)
21
0,35.
60
Для второго случая (t = 35) вероятность ищем через обратное
событие:
21
P( X 35) 1 P( X 35) 1
35
1 0,6 0,4.
Аскарова А.Ж.

32.

Закон больших чисел
Пафнутий Львович Чебышёв (18211894) — русский математик и механик,
основоположник петербургской
математической школы,
академик Петербургской академии
наук и ещё 24 академий мира.
Ирене-Жюль Бьенеме (1796—1878) —
французский статистик и администратор
Аскарова А.Ж.

33.

Закон больших чисел
Утверждение 7 (неравенство Бьенеме-Чебышева)
Пусть X - случайная величина, с математическим
ожиданием m и средним квадратическим
отклонением . Тогда a 0,
2
P X m 2 .
Аскарова А.Ж.

34.

Закон больших чисел
Неравенство Чебышева утверждает, что каково бы
ни было положительное число ε, вероятность того,
что случайная величина X отклонится от своего
математического ожидания не меньше, чем на ε,
ограничена сверху величиной D/ ε2 :
Неравенство Чебышева дает грубую оценку сверху и
утверждает, что для любой случайной величины Х
вероятность того, что она отклонится на ε от m
меньше, чем дисперсия, деленная на ε2 .
Аскарова А.Ж.

35.

Закон больших чисел
Доказательство: Пусть Y X m .
2
Y - положительная случайная величина и
E Y V X 2 .
Маркова,
PY
Используя неравенство
2
E Y
2
,
Y X m X m ,
2
2
2
тогда
2
P X m 2 .
Аскарова А.Ж.

36.

Закон больших чисел
Замечание :
Это означает, что вероятность того, что X
отклоняется от своего среднего значения по крайней
2
мере на , меньше, чем 2 .
Чем больше , тем меньше вероятность.
2
Мы можем написать также, P m X m 1 2 .
Аскарова А.Ж.

37.

Закон больших чисел
Утверждение 8. ПустьX 1 ,..., X n независимые
переменные с одинаковым законом, с
математическим ожиданием m. Тогда 0,
X 1 ... X n
lim P
m 0.
n
n
Доказательство: Обозначим
X 1 ... X n
Mn
,
n
1 n
1 n
E M n E X i m , V M n 2 V X i .
n i 1
n i 1
Аскарова А.Ж.

38.

Закон больших чисел
1 n
2
,
Мы допускаем что, V M n 2 V X i
n
n i 1
поскольку X i независимы. Используя неравенство
2
Бьенеме-Чебышева:
Таким образом,
X 1 ... X n
0 P
m n2 .
n
X 1 ... X n
lim P
m 0.
n
n
Аскарова А.Ж.

39.

Закон больших чисел
Закон больших чисел действует во многих
физических явлениях.
Пример. Газ состоит из множества беспорядочно
движущихся молекул. Предсказать поведение одной
молекулы невозможно, но совокупное их действие
подчиняется закону больших чисел. Например,
давление газа, которое определяется суммарным
воздействием молекул на единицу площади, должно
быть
практически
постоянным,
что
и
наблюдается в действительности.
Аскарова А.Ж.

40.

Закон больших чисел
Теорема
Чебышева
выборочного
метода,
служит
широко
обоснованием
применяемого
в
статистике, когда по случайной выборке судят обо
всей
совокупности
исследуемых
объектов.
Например, оценивают качество партии конфет по
сравнительно небольшой пробе, считая, что проба
содержит все же достаточно много конфет для того,
чтобы проявлялось действие закона больших чисел.
Аскарова А.Ж.

41.

Вычисление с помощью компьютера
Предположим, у нас есть функция random, которая
выдает наугад вещественное значение в [0,1].
- программу, которая моделирует переменную Бернулли с
параметром p:
a=random
if a<p then x=1 else x=0
- программа, моделирующая переменную X: X 1,2,3 ,
P X 1 0.2 , P X 2 0.5 , P X 3 0.3
a=random
if a<0.2 then x=1
else if a<0.7 then x=2 else x=3
Аскарова А.Ж.