Методы оптимизации

1.

Методы оптимизации
Мелехин Александр Алексеевич
преподаватель кафедры Е1

2.

Что такое методы оптимизации и зачем они нужны?
Методы оптимизации — это математические и вычислительные инструменты, которые
позволяют:
- повысить эффективность технических систем (минимизация затрат, энергопотребления,
времени выполнения и т. д.);
- найти лучшие решения среди множества возможных (например, оптимальная конфигурация
системы);
- улучшить производительность, надежность и устойчивость систем.
2

3.

Роль системного анализа в проектировании технических систем
Системный анализ — это методология, позволяющая:
- разделять сложную систему на подсистемы и анализировать их взаимодействие;
- определять ключевые параметры системы, которые подлежат оптимизации;
- выявлять конфликтующие требования (например, повышение надежности при минимальных
затратах).
3

4.

Какие методы оптимизации наиболее важны
для технических систем?
- Линейное и нелинейное программирование – для поиска оптимальных параметров
конструкции.
Примеры задач линейного программирования.
Производственная задача. Предприятие выпускает некоторые изделия, для их производства
необходимы различные ресурсы. Задано, сколько и каких ресурсов необходимо для каждого
изделия, сколько ресурсов имеется, и сколько предприятие выручит за продажу произведённых
изделий. Необходимо выбрать, какие изделия и в каком количестве выпускать, чтобы прибыль
предприятия была максимальной.
Примеры задач нелинейного программирования.
Квадратичные задачи. В них целевая функция представляет собой полином второй степени, а
система ограничений линейна.
4

5.

Какие методы оптимизации наиболее важны
для технических систем?
- Методы градиентного спуска – для сложных многопараметрических задач.
Иллюстрация последовательных приближений к
точке экстремума в направлении наискорейшего
спуска (красн.) в случае дробного шага. Синим
отмечены линии уровня.
5

6.

Какие методы оптимизации наиболее важны
для технических систем?
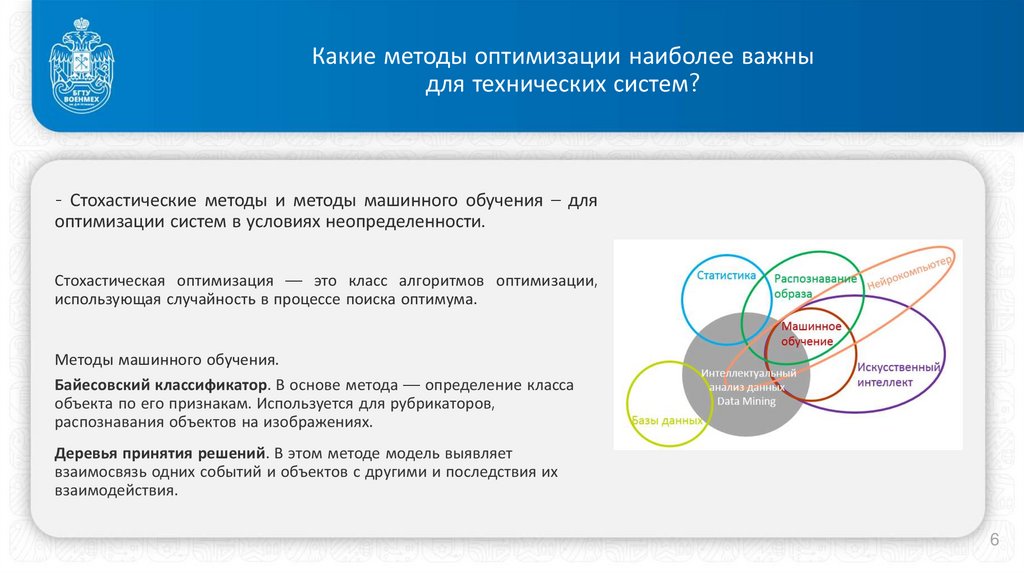
- Стохастические методы и методы машинного обучения – для
оптимизации систем в условиях неопределенности.
Стохастическая оптимизация — это класс алгоритмов оптимизации,
использующая случайность в процессе поиска оптимума.
Методы машинного обучения.
Байесовский классификатор. В основе метода — определение класса
объекта по его признакам. Используется для рубрикаторов,
распознавания объектов на изображениях.
Деревья принятия решений. В этом методе модель выявляет
взаимосвязь одних событий и объектов с другими и последствия их
взаимодействия.
6

7.

Как методы оптимизации помогают
в реальной инженерной практике?
- Оптимизация конструкций (например, минимизация массы ствола артиллерийского орудия при
сохранении прочности).
- Оптимизация производственных процессов (например, минимизация отходов в производстве).
- Улучшение автоматизированных систем управления (например, интеллектуальные системы
распределения нагрузки в электросетях).
7

8.

Как связаны оптимизация и цифровые технологии?
- Использование искусственного интеллекта и нейросетей для оптимизации сложных систем.
- Применение цифровых двойников для виртуального тестирования и оптимизации.
- Использование Big Data для нахождения лучших решений в реальном времени.
8

9.

Методы оптимизация в зависимости от числа переменных
Методы оптимизации делятся на одномерные и многомерные в зависимости от числа переменных,
участвующих в процессе поиска экстремума (минимума или максимума) функции.
1. Одномерная оптимизация (одномерные методы оптимизации применяются, когда целевая функция
зависит только от одной переменной).
Метод дихотомии (деления пополам):
- разделяет интервал пополам и отбрасывает ту часть, где минимум невозможен;
- быстро сходится, но требует вычисления функции в новых точках.
Метод золотого сечения:
- улучшенная версия метода дихотомии, использует пропорцию золотого сечения;
- обеспечивает экономию вычислений и гарантированную сходимость.
9

10.

Методы оптимизация в зависимости от числа переменных
1. Одномерная оптимизация (одномерные методы оптимизации применяются, когда целевая функция
зависит только от одной переменной).
Метод Фибоначчи:
- похож на золотое сечение, но использует числа Фибоначчи для выбора точек;
- оптимален по числу итераций.
Метод Ньютона (метод касательных):
- использует производную и вторую производную функции;
- быстро сходится, но требует вычисления производных, что не всегда возможно.
10

11.

Методы оптимизация в зависимости от числа переменных
2. Многомерная оптимизация (когда функция зависит от нескольких переменных).
Градиентные методы:
- метод градиентного спуска – идет в направлении антиградиента, уменьшая функцию;
- метод Ньютона – использует не только градиент, но и гессиан (матрицу вторых производных), что ускоряет
сходимость.
Методы без градиента (неградиентные):
- метод наискорейшего спуска – выбирает направление, в котором функция убывает быстрее всего;
- методы случайного поиска – полезны, когда градиент трудно вычислить.
11

12.

Спасибо за внимание!