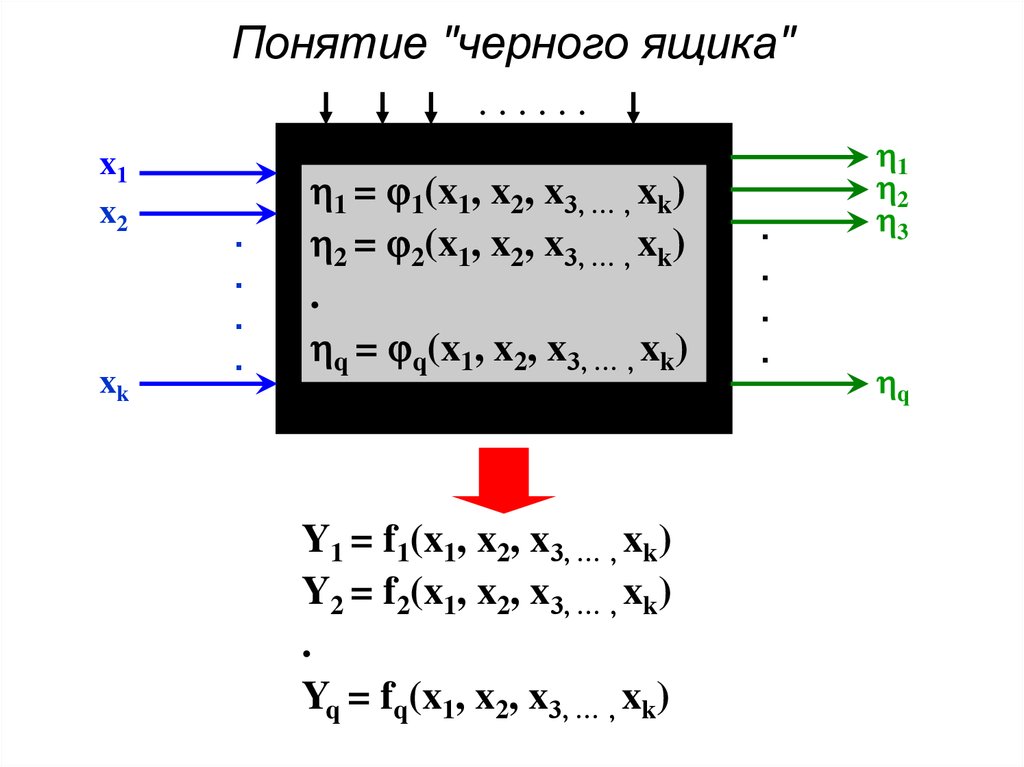
Понятие "черного ящика"

1.

2. Понятие "черного ящика"

Понятие "черного ящика"
......
x1
x2
xk
.
.
.
.
1 = 1(x1, x2, x3, … , xk)
2 = 2(x1, x2, x3, … , xk)
.
q = q(x1, x2, x3, … , xk)
Y1 = f1(x1, x2, x3, … , xk)
Y2 = f2(x1, x2, x3, … , xk)
.
Yq = fq(x1, x2, x3, … , xk)
.
.
.
.
1
2
3
q

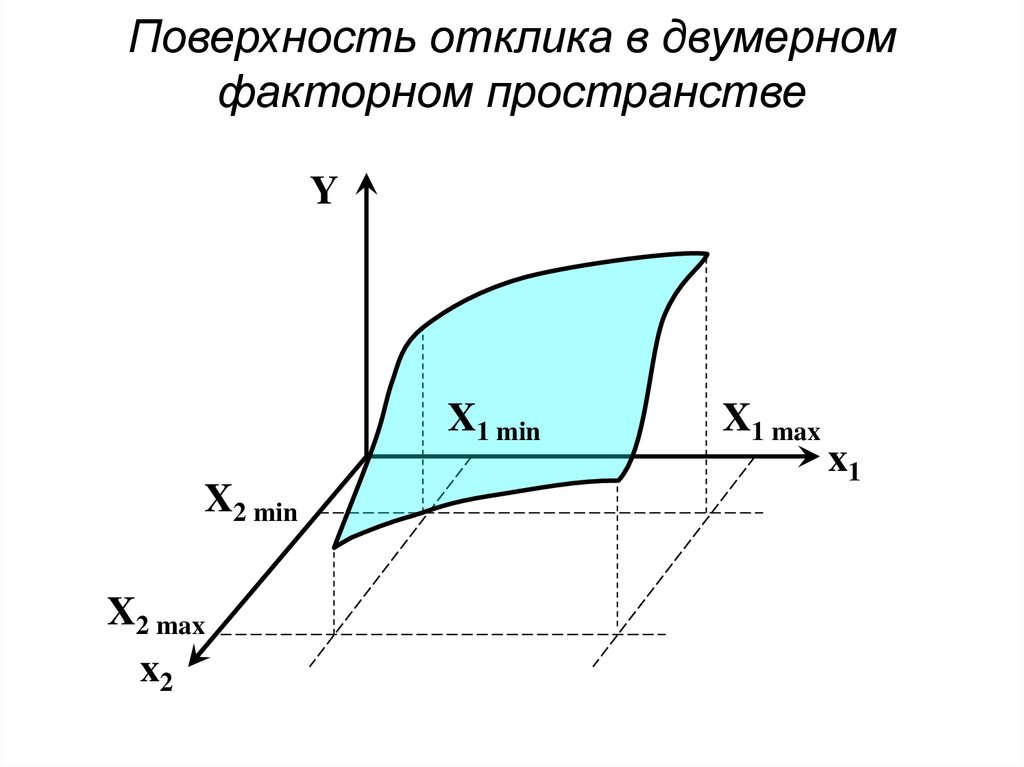
3. Поверхность отклика в двумерном факторном пространстве

Y
X1 min
X2 min
X2 max
x2
X1 max
x1

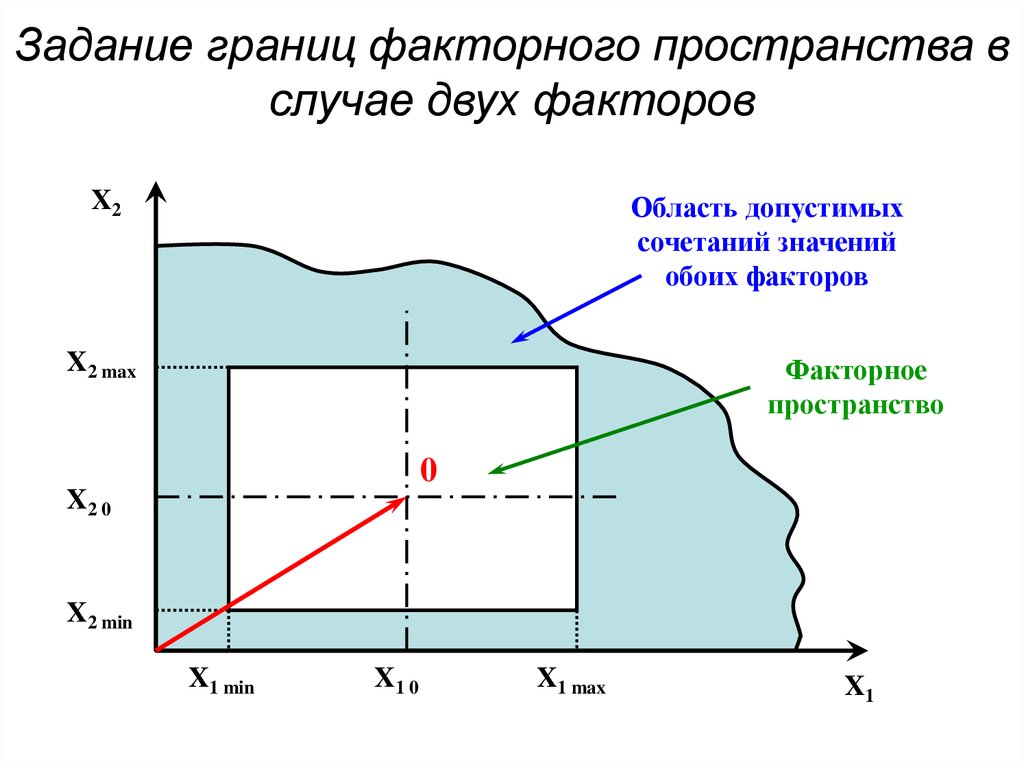
4. Задание границ факторного пространства в случае двух факторов

X2
Область допустимых
сочетаний значений
обоих факторов
X2 max
Факторное
пространство
0
X2 0
X2 min
X1 min
X1 0
X1 max
X1

5. Разложение неизвестной функции в ряд Тейлора

( x1 , x 2 , x 3 ...x k )
k
k
k
i 1
i 1
i 1
0 i x i ijx i x j ii x ...
2
i
где
i
x i
ij
x i x j
2
ii 2
x i
2

6. Пересчет реальных значений факторов в масштабные

xi
Xi Xi0
X i
Xi
X i min X i max
2
X i max X i min
2
xi – масштабное значение i-го фактора ( 1 …+1)
Xi – реальное значение i-го фактора
Xi min – минимальное реальное значение i-го фактора
Xi max – максимальное реальное значение i-го фактора
Xi интервал варьирования

7.

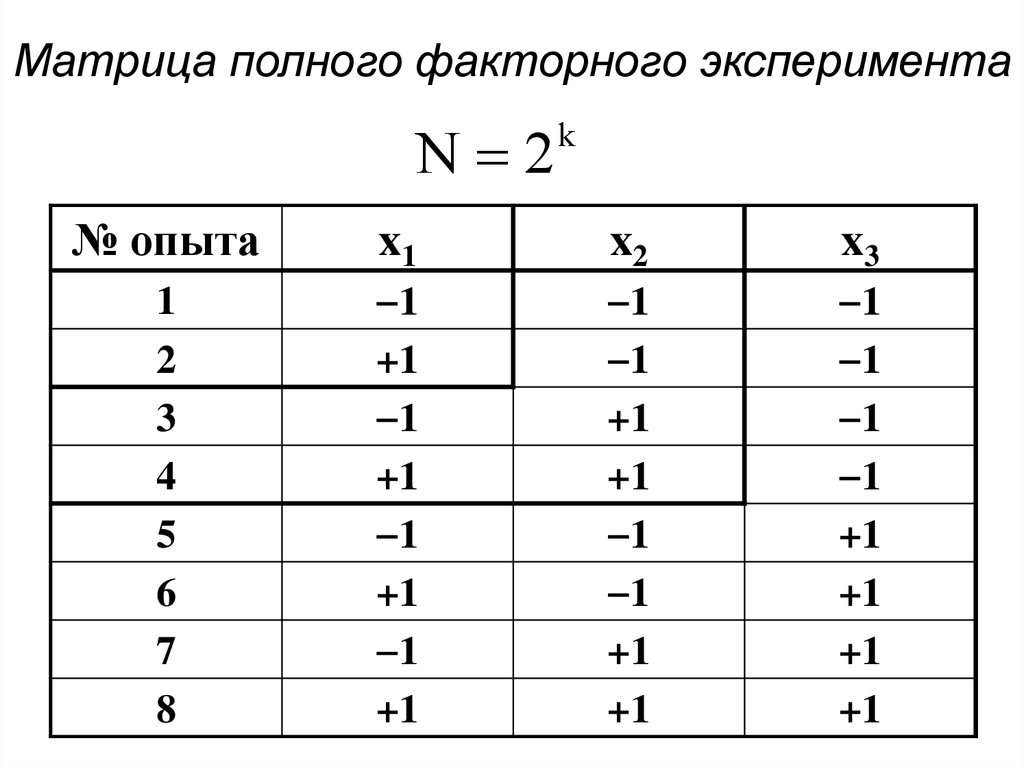
Матрица полного факторного эксперимента
N 2
k
№ опыта
x1
x2
x3
1
2
3
4
5
6
7
8
1
+1
1
+1
1
+1
1
+1
1
1
+1
+1
1
1
+1
+1
1
1
1
1
+1
+1
+1
+1

8. Свойства полных факторных экспериментов

Расширенная матрица плана 22
№ опыта
x0
x1
x2
x1x2
y
1
+1
1
1
+1
y1
2
+1
+1
1
1
y2
3
+1
1
+1
1
y3
4
+1
+1
+1
+1
y4
N
Симметричность
x iu
0
u 1
N
Нормированность
x
u 1
N
Ортогональность
2
iu
N
x iu x ju
u 1
0

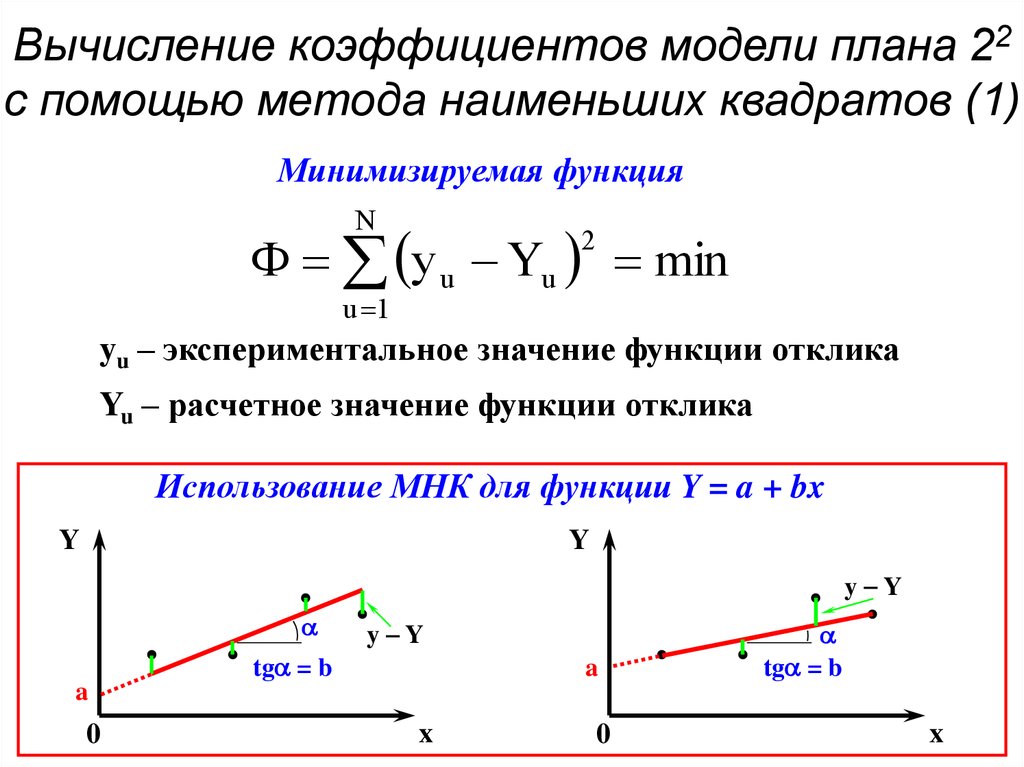
9. Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (1)

Минимизируемая функция
N
y u Yu min
2
u 1
yu – экспериментальное значение функции отклика
Yu – расчетное значение функции отклика
Использование МНК для функции Y = a + bx
Y
Y
y Y
y Y
tg = b
a
tg = b
a
0
x
0
x

10. Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (2)

Yu b 0 x 0 u b1 x 1u b 2 x 2 u
N
y u b 0 u b1u x 1u b 2 u x 2 u min
2
u 1
0
b 0
0
b1
0
b 2

11. Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (3)

N
N
N
N
u 1
u 1
u 1
b 0 x b1 x 0 u x1u b 2 x 0 u x 2 u x 0 u y u
u 1
2
0u
N
N
N
N
u 1
u 1
u 1
u 1
N
N
N
u 1
u 1
u 1
b 0 x 0 u x 1u b1 x 12u b 2 x 1u x 2 u x 1u y u
b 0 x 0 u x 2 u b1 x 1u x 2 u b 2 x
2
2u
N
x 2u y u
u 1

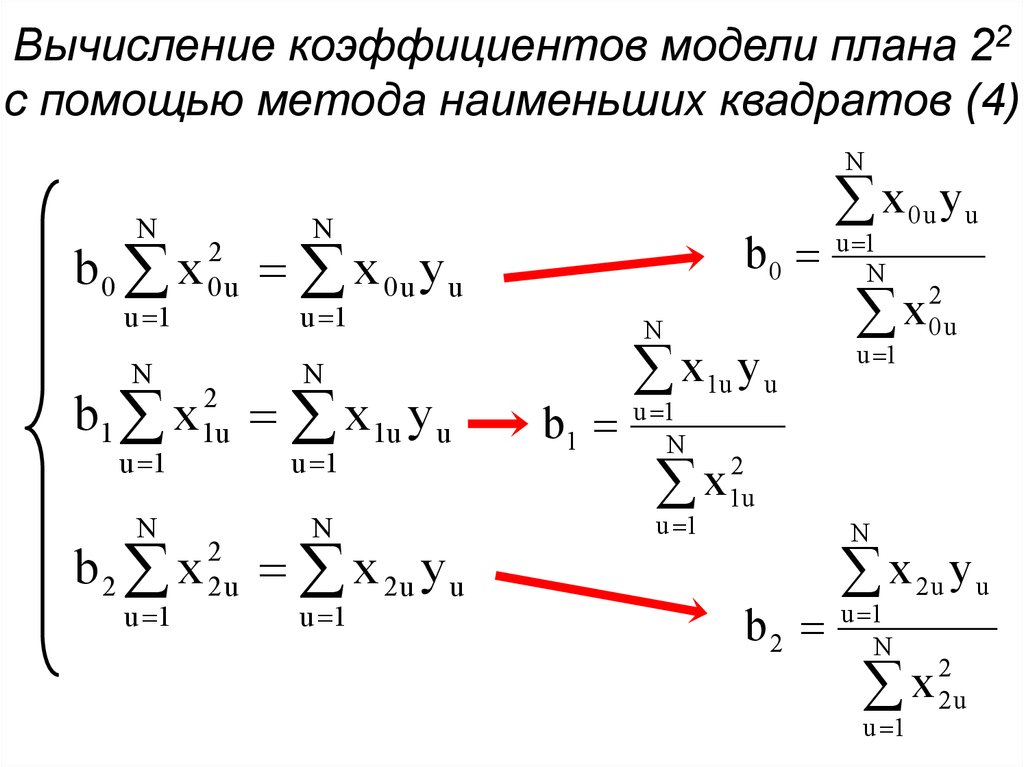
12. Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (4)

N
N
b0 x
u 1
N
b1 x
u 1
N
2
1u
b2 x
u 1
2
0u
2
2u
N
b0
x 0u y u
u 1
N
N
x 1u y u
u 1
N
x 2u y u
u 1
b1
x 1u y u
u 1
N
x
u 1
x 0u yu
u 1
N
x
u 1
2
0u
2
1u
N
b2
x 2u y u
u 1
N
x
u 1
2
2u

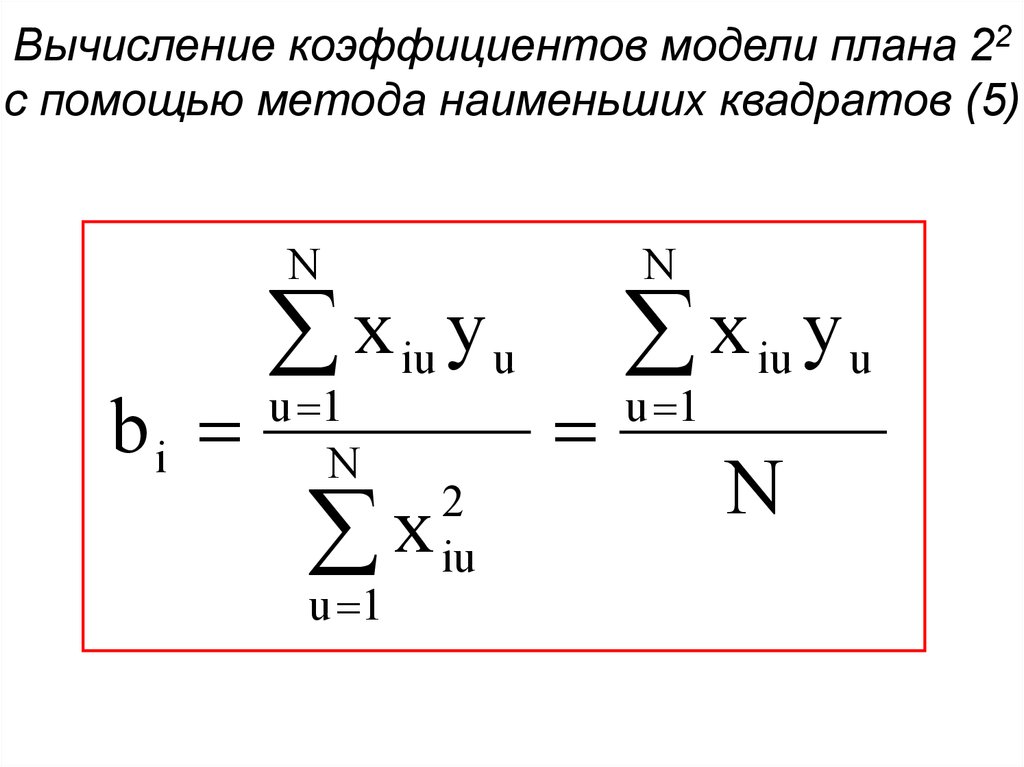
13. Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (5)

N
bi
x iu y u
u 1
N
x
u 1
2
iu
N
x iu y u
u 1
N

14. Расчет среднего значения и дисперсии функции отклика при дублировании опытов в центре плана

y0
y g0
g 1
n0
y g 0 y 0
n0
n0
S
2
y
g 1
f
y g 0 y 0
n0
2
2
g 1
n 0 1
y0 – среднее значение функции отклика в центре плана
yg 0 – результат g-го дублирования в центре плана
f – число степеней свободы
n0 – число дублирований опытов в центре плана
S2y – дисперсия опыта

15. Расчет средних значений и дисперсии опытов при неравномерном дублировании

nu
yu
y gu
g 1
2
yu
S
nu
N
S 2y
y
nu
f uS
u 1
N
2
yu
fu
u 1
g 1
yu
2
gu
fu
g 1
yu
2
gu
nu 1
y g u y u
N nu
y
nu
2
u 1 g 1
N
n u 1
u 1
yu – среднее значение функции отклика в u-м опыте
yg u – результат g-го дублирования u-го опыта
fu – число степеней свободы для u-го опыта
nu – число дублирований u-го опыта
S2yu – дисперсия u-го опыта S2y – дисперсия опытов (средняя)

16. Расчет средних значений и дисперсии опытов при равномерном дублировании

nu = n
yu
fu = f
N
S2y
y gu
n
fu S
u 1
N
fu
S2y u
g 1
2
yu
N
yg u y u
n
n
fu S
u 1
2
yu
N fu
g 1
f
N
S
u 1
2
yu
N
2
g 1
n 1
yg u yu
N
yg u y u
n
2
n
2
u 1 g 1
N n 1
u 1
yu – среднее значение функции отклика в u-м опыте
yg u – результат g-го дублирования u-го опыта
fu = f – число степеней свободы для любого опыта
nu = n – число дублирований любого опыта
S2yu – дисперсия u-го опыта S2y – дисперсия опытов (средняя)

17. Проверка ряда дисперсий на однородность по критерию Кохрена при равномерном дублировании

Ряд дисперсий однороден, если Gрасч Gтабл
Расчетное значение
критерия Кохрена
G расч
2
y u max
N
2
yu
u 1
S
S
Табличное значение
критерия Кохрена
G табл N, f,
f n - 1
S2y u max – максимальная дисперсия опыта
S2y u – дисперсия u-го опыта
N – число экспериментов
f – число степеней свободы
– уровень значимости

18. Проверка статистической значимости коэффициентов уравнения регрессии

Коэффициент значим, если bi ≥ bi
bi S t
2
bi
При дублировании
опытов в центре плана
S
2
bi
S
При равномерном
дублировании опытов
2
y
S
2
bi
N
2
y
S
N n
bi – доверительный интервал
S2bi – дисперсия оценок коэффициентов
S2y – дисперсия опытов (средняя) N – число экспериментов
n – число дублирований опытов
t – критерий Стьюдента
t = ( , f), где f = n0 – 1
или
t = ( , f1), где f1 = N(n – 1)

19. Проверка значимости уравнения регрессии (1)

Уравнение значимо, если Fрасч ≤ Fтабл
2
Sнеад
Fрасч 2
Sy
N
При дублировании
2
S
опытов в центре
неад
плана
Yu y u
N
2
u 1
f2
N
Yu y u
2
u 1
N k'
N
n Yu y u
n Yu y u
При равномерном
2
u 1
u 1
S
дублировании
неад
f2
N k'
опытов
S2неад – дисперсия неадекватности
Yu – расчетное значение функции отклика для u-го опыта
yu, yu – экспериментальное значение для u-го опыта
k’ – число значимых коэффициентов уравнения регрессии
2
2

20. Проверка значимости уравнения регрессии (2)

N
Yu yu
При дублировании
опытов в центре Fрасч
плана
N
2
Y
y
u u
2
u 1
u 1
f2
yg 0 y0
n0
2
g 1
yg 0 y0
n0
n0 1
N
n Yu y u
N
n Yu y u
2
u 1
2
u 1
f2
y u g y u
N
2
g 1
f
При равномерном
дублировании
Fрасч
опытов
N k'
n
2
u 1 g 1
f1
N k'
y u g y u
N
n
u 1 g 1
N n 1
2

21. Проверка значимости уравнения регрессии (3)

При дублировании опытов в центре плана
Fтабл = (f, f2)
При равномерном дублировании опытов
Fтабл = (f1, f2)
f2 – число степеней свободы в числителе
f, f1 – число степеней свободы в знаменателе
r
2
Y
y
m m
m 1
При N = k’ f2 = 0
Fрасч
r – число дополнительных опытов
r
S2y

22. Преобразование уравнения регрессии под реальное представление факторов

Вид уравнения для масштабного представления факторов
Y 18,3 3 x1 1,5 x 2
Y – прочность порошкового материала
x1 – температура спекания (900 1100 oC)
x2 – время изотермической выдержки (10 30 мин)
Пересчет реальных значений факторов в масштабные
X1 1000
x1
100
X 2 20
x2
10
Вид уравнения для реального представления факторов
Y 14,7 0,03 X1 0,15 X 2

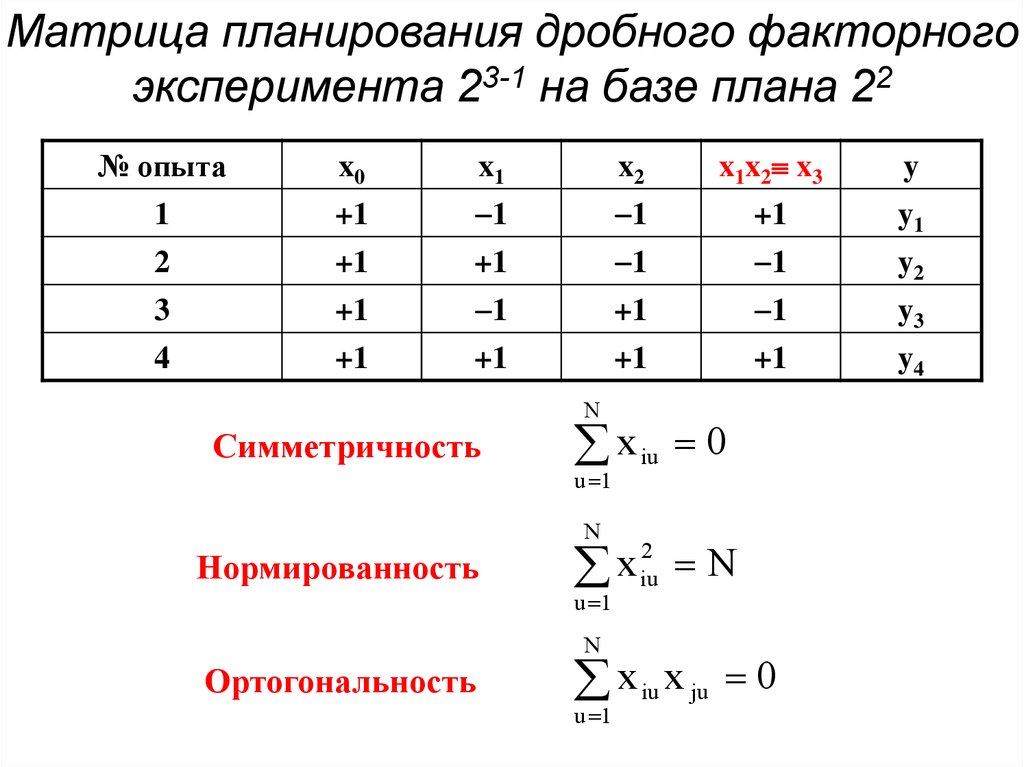
23. Матрица планирования дробного факторного эксперимента 23-1 на базе плана 22

№ опыта
x0
x1
x2
x1x2 x3
y
1
+1
1
1
+1
y1
2
+1
+1
1
1
y2
3
+1
1
+1
1
y3
4
+1
+1
+1
+1
y4
N
Симметричность
x iu
0
u 1
N
Нормированность
2
x
iu N
u 1
N
Ортогональность
x iu x ju
u 1
0

24. Смешивание эффектов в дробных факторных экспериментах

№
опыта
1
2
3
4
x1
x2
x3
x1x2
x 2x 3
x 1x 3
–1
+1
–1
+1
–1
–1
+1
+1
+1
–1
–1
+1
+1
–1
–1
+1
–1
+1
–1
+1
–1
–1
+1
+1
b1 β1 + β23
b2 β2 + β13
b3 β3 + β12

25. Понятия генерирующего соотношения и определяющего контраста

Генерирующее соотношениеx3 x1x2
x32 x1x2x3
Определяющий контраст
1 x1x2x3
1 x1x2x3
x1 x12x2x3
x1 x2x3
x2 x1x22x3
x2 x1x3
x3 x1x2x32
x3 x1x2

26. Матрица ДФЭ 24-1с определяющим контрастом 1  x1x2x3x4

Матрица ДФЭ 24-1с определяющим
контрастом 1 x1x2x3x4
№ опыта
x1
x2
x3
x4 x1x2x3
1
–1
–1
–1
–1
2
3
+1
–1
–1
+1
–1
–1
+1
+1
4
+1
+1
–1
–1
5
–1
–1
–1
+1
6
+1
–1
–1
–1
7
–1
+1
–1
–1
8
+1
+1
–1
+1
b1 β1 + β234
b2 β2 + β134
b3 β3 + β124
b4 β4 + β123
b12 β12 + β34
b13 β13 + β24
b14 β14 + β23
b23 β23 + β14
b34 β34 + β12
Y = b0 + b1x1 + b2x2 + b3x3 + b4x4

27. Матрица ДФЭ 24-1с определяющим контрастом 1  x1x2x4

Матрица ДФЭ 24-1с определяющим
контрастом 1 x1x2x4
№ опыта
x1
x2
x3
x4 x1x2
1
–1
–1
–1
+1
2
3
+1
–1
–1
+1
–1
–1
–1
–1
4
+1
+1
–1
+1
5
–1
–1
–1
+1
6
+1
–1
–1
–1
7
–1
+1
–1
–1
8
+1
+1
–1
+1
b1 β1 + β24
b2 β2 + β14
b3 β3 + β1234
b4 β4 + β12
b13 β13 + β234
b23 β 23 + β134
b34 β34 + β123
b24 β24 + β1
Y = b0 + b1x1 + b2x2 + b3x3 + b4x4 + b13x1x3 + b23x2x3 + b34x3x4

28. Планы второго порядка

k
k
k
i 1
k
i 1
k
i 1
k
0 i x i ij x i x j ii x i2
Y b 0 b i x i b ij x i x j b ii x i2
i 1
i 1
i 1
– истинная величина функции отклика
Y – оценка величины функции отклика
i, ij, ii – истинные значения коэффициентов регрессии
bi, bij, bii – оценки коэффициентов регрессии
Число членов модели
C
k
k 2
k 2 ! k! k 1 k 2 k 1 k 2
k! 2!
k! 2
Число опытов
k 1 k 2
N
2
2

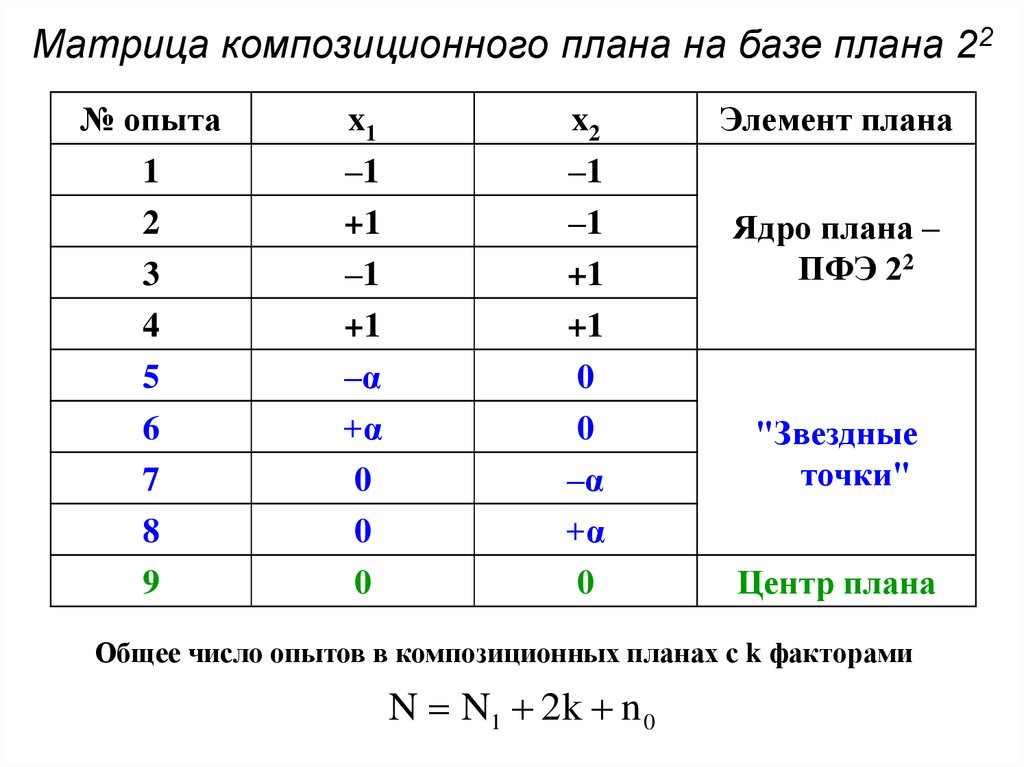
29. Матрица композиционного плана на базе плана 22

№ опыта
x1
x2
1
2
3
4
5
6
7
8
9
–1
+1
–1
+1
–α
+α
0
0
0
–1
–1
+1
+1
0
0
–α
+α
0
Элемент плана
Ядро плана –
ПФЭ 22
"Звездные
точки"
Центр плана
Общее число опытов в композиционных планах с k факторами
N N1 2k n 0

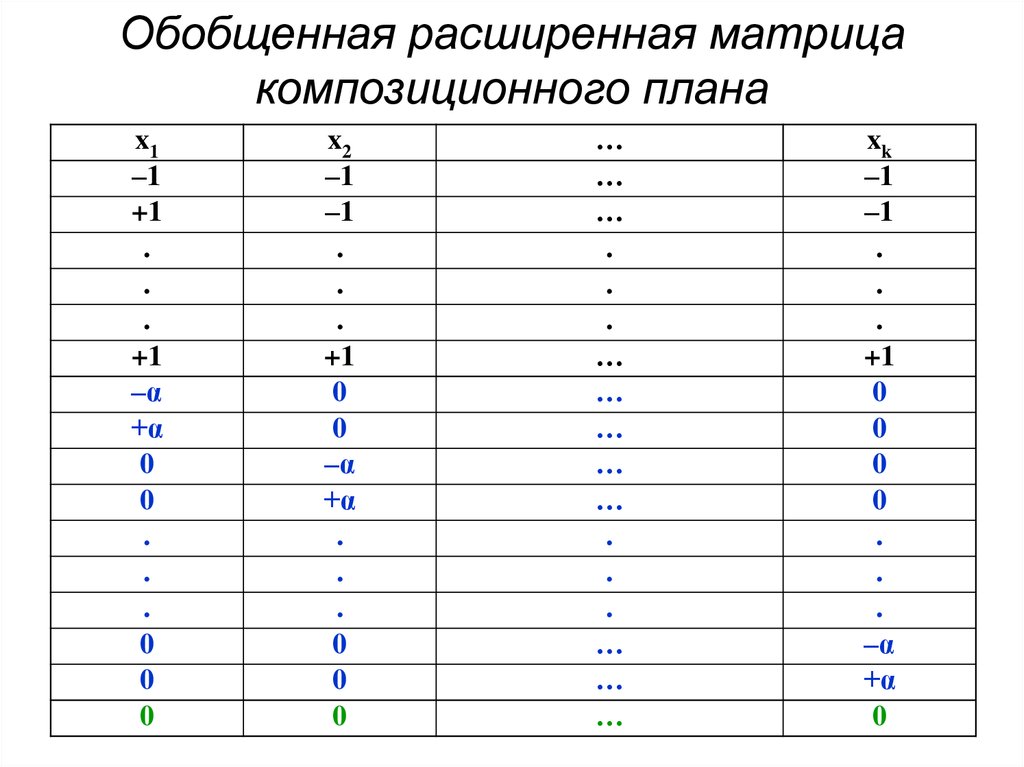
30. Обобщенная расширенная матрица композиционного плана

x1
–1
+1
.
.
.
+1
–α
+α
0
0
.
.
.
0
0
0
x2
–1
–1
.
.
.
+1
0
0
–α
+α
.
.
.
0
0
0
…
…
…
.
.
.
…
…
…
…
…
.
.
.
…
…
…
xk
–1
–1
.
.
.
+1
0
0
0
0
.
.
.
–α
+α
0

31. Нечетные моменты плана

N
x iu
u 1
N
N
(x i x j )u
( x i x jx )u
u 1
u 1
N
(x x j )u
u 1
При всех видах дублирования
N
x iu 0
u 1
N
(x i x j )u 0
u 1
N
(x i x jx )u 0
u 1
2
i
N
3
x
iu
u 1

32. Четные моменты плана

N
x
u 1
2
iu
N
N
(x x )
u 1
2
i
4
x
iu
2
j u
u 1
При дублировании опытов в
центре плана и равномерном
дублировании
При неравномерном
дублировании
N
N
1
2 x iu2
N u 1
1 N 2 2
3 (x i x j )u
N u 1
1 N 4
4 xi u
N u 1
2
2
n
x
u iu
u 1
N
nu
N
4
u 1
u 1
N
nu
u 1
N
3
4
n
x
u iu
2 2
n
(
x
u i x j )u
u 1
N
nu
u 1

33. Вспомогательные коэффициенты для расчета коэффициентов уравнений регрессии композиционных планов

k 22
a
1
2
4 3 k 3 k 2
1
c
4 3
2
b
1
2
4 3 k 3 k 2
3 22
d
2
4 3 4 3 k 3 k 2
Проверка правильности расчетов вспомогательных
коэффициентов
a b k 2 1
b d k c 2 0
b 2 d k 1 c 3 d 4 0

34. Расчет коэффициентов уравнения регрессии композиционных планов (1)

При дублировании опытов в центре плана и равномерном дублировании
a N
b k N 2
b 0 Yu x iu Yu
N u 1
N i 1 u 1
1 N
bi
x iu Yu
N 2 u 1
1 N
x i x j u Yu
bij
N 3 u 1
c N 2
d k N 2
b N
bii x iu Yu x iu Yu Yu
N u 1
N i 1 u 1
N u 1

35. Расчет коэффициентов уравнения регрессии композиционных планов (2)

При неравномерном дублировании опытов
b0
a
N
n u Yu
n u u 1
u 1
bi
N
2 n u
N
bii
N
N
n u x iu Yu
bij
u 1
nux
n u u 1
u 1
N
n u x
n u i 1 u 1
2
iu
Yu
N
n u x i x j u Yu
N
1
3 n u
u 1
u 1
u 1
c
k
u 1
N
1
b
N
2
iu
Yu
d
N
k
N
n u x
n u i 1 u 1
u 1
2
iu
Yu
b
N
N
n u Yu
n u u 1
u 1

36. Дисперсия оценки коэффициентов регрессии

При дублировании
опытов в центре
плана
a 2
2
Sb SY
N
При неравномерном При равномерном
дублировании
дублировании
S
2
b0
0
1 2
S
SY
N 2
2
bi
1 2
S
SY
N 3
2
bij
c d 2
2
Sb
SY
N
ii
a
N
nu
S2Y
u 1
S
2
bi
1
N
2 n u
S2Y
u 1
S
2
b ij
1
N
3 n u
S
c d
N
nu
u 1
1
S
S2Y
N n 2
2
bi
S2Y
1
S
S2Y
N n 3
S2Y
c d 2
S
SY
Nn
u 1
2
b ii
a 2
S
SY
Nn
2
b0
2
bij
2
b ii

37. Условие D-оптимальности для непрерывных симметричных планов

При k = 1
3
k 3
2
1 k 1
k 1 k 2
2
При k > 1
2k 1 4k 4 12k 17
3
2
4 k 2
2 4

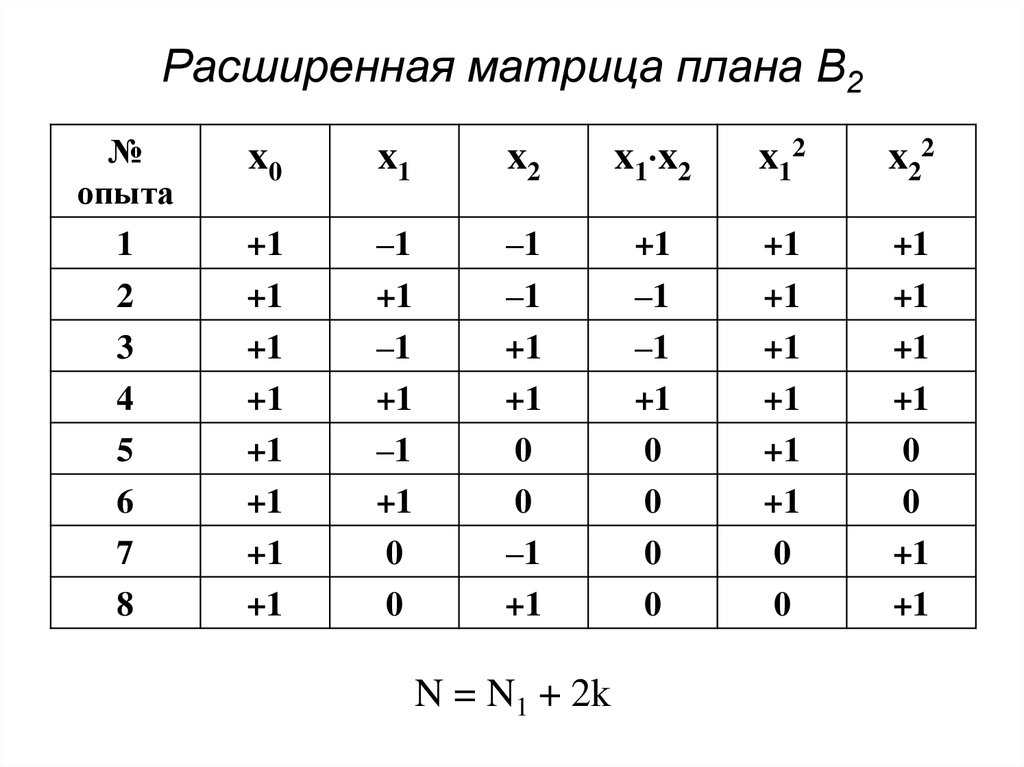
38. Расширенная матрица плана B2

№
опыта
1
2
3
4
5
6
7
8
x0
x1
x2
x1 x2
x 12
x22
+1
+1
+1
+1
+1
+1
+1
+1
–1
+1
–1
+1
–1
+1
0
0
–1
–1
+1
+1
0
0
–1
+1
+1
–1
–1
+1
0
0
0
0
+1
+1
+1
+1
+1
+1
0
0
+1
+1
+1
+1
0
0
+1
+1
N = N1 + 2k

39. Расширенная матрица плана B3

№ опыта
x0
x1
x2
x3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
–1
+1
–1
+1
–1
+1
–1
+1
–1
+1
0
0
0
0
–1
–1
+1
+1
–1
–1
+1
+1
0
0
–1
+1
0
0
–1
–1
–1
–1
+1
+1
+1
+1
0
0
0
0
–1
+1
x1 x2 x2 x3 x1 x3
+1
–1
–1
+1
+1
–1
–1
+1
0
0
0
0
0
0
+1
+1
–1
–1
–1
–1
+1
+1
0
0
0
0
0
0
+1
–1
+1
–1
–1
+1
–1
+1
0
0
0
0
0
0
x12
x22
x32
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
0
0
0
0
+1
+1
+1
+1
+1
+1
+1
+1
0
0
+1
+1
0
0
+1
+1
+1
+1
+1
+1
+1
+1
0
0
0
0
+1
+1

40. Расчет коэффициентов уравнения регрессии композиционного плана Bk

При дублировании опытов в центре плана
N
k
N
b0 с1 Yu с 2 x iu2 Yu
u 1
i 1 u 1
bij с 4 x i x j u Yu
N
N
bi с3 x iu Yu
u 1
N
u 1
k
N
N
bii с5 x Yu с6 x Yu с 2 Yu
u 1
2
iu
i 1 u 1
2
iu
u 1
При дублировании опытов в центре плана величина Yu меняется на
величину Yu

41. Расчет дисперсий и среднеквадратических ошибок оценок коэффициентов

При дублировании опытов в центре плана
S2b с1S2Y
S2b с3S2Y
S2b с4S2Y
S2b c5 c6 S2Y
Sb с7SY
S b с 8S Y
Sb с9SY
Sb с10SY
0
0
i
i
ij
ij
ii
ii
При равномерном дублировании опытов
2
с
S
S2b 1 Y
n
с 7SY
Sb
n
0
0
2
с
S
S2b 3 Y
n
с8SY
Sb
n
i
i
2
с
S
S2b 4 Y
n
с9SY
Sb
n
ij
ij
S2b
ii
c5 c6 S2Y
с10SY
Sb
n
ii
n

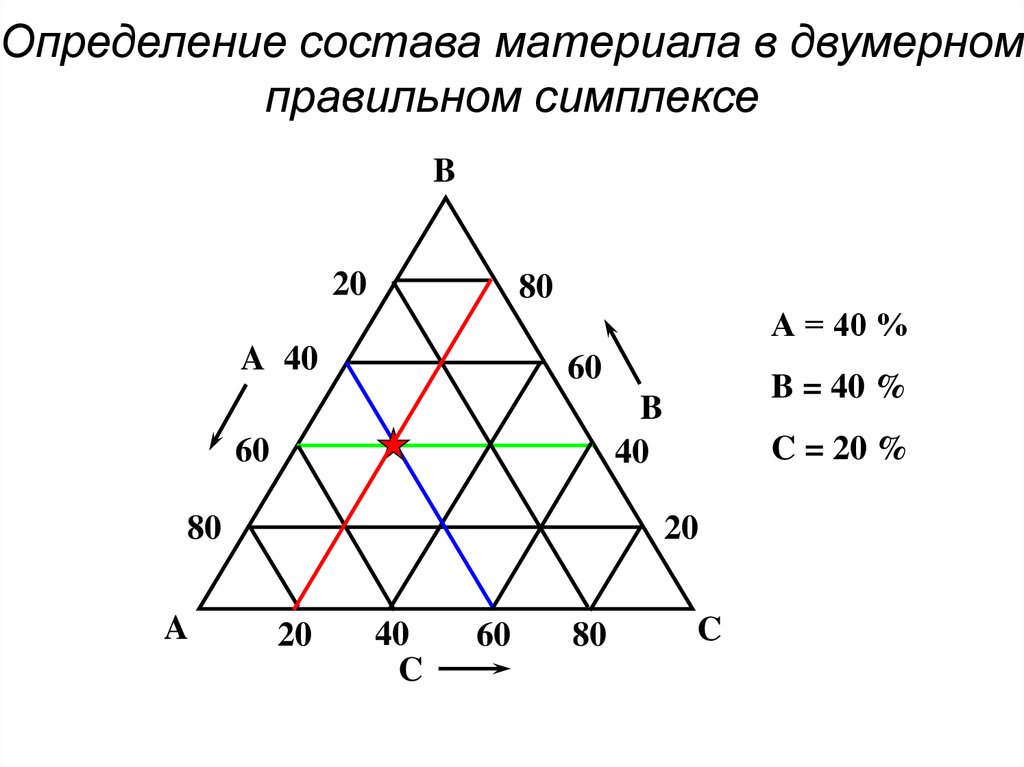
42. Определение состава материала в двумерном правильном симплексе

B
20
80
А = 40 %
A 40
60
B
40
60
80
A
B = 40 %
C = 20 %
20
20
40
C
60
80
C

43. Преобразование полиномиального регрессионного уравнения в каноническую форму Шеффе (1)

Исходное
уравнение
Правило
нормировки
k
k
k
i 1
i 1
i 1
Y b0 bi x i bijx i x j bii x i2
q
xi
i 1
b0 = b0 x1 + b0 x2 + b0 x3
x12 = x1 – x1x2 – x1x3 = x1(1 – x2 – x3)
x22 = x2 – x1x2 – x2x3 = x2(1 – x1 – x3)
x32 = x3 – x1x3 – x2x3 = x3(1 – x1 – x2)
1

44. Преобразование полиномиального регрессионного уравнения в каноническую форму Шеффе (2)

Y = (b0 + b1 + b11)x1 + (b0 + b2 + b22)x2 + (b0 + b3 + b33)x3
+ (b12 – b11 – b22)x1x2 + (b13 – b11 – b33)x1x3 +
+ (b23 – b22 – b33)x2x3
i = b0 + bi + bii
ij = bij – bii – bij
Каноническая форма Шеффе
Y = 1x1 + 2x2 + 3x3 + 12x1x2 + 13x1x3 + 23x2x3

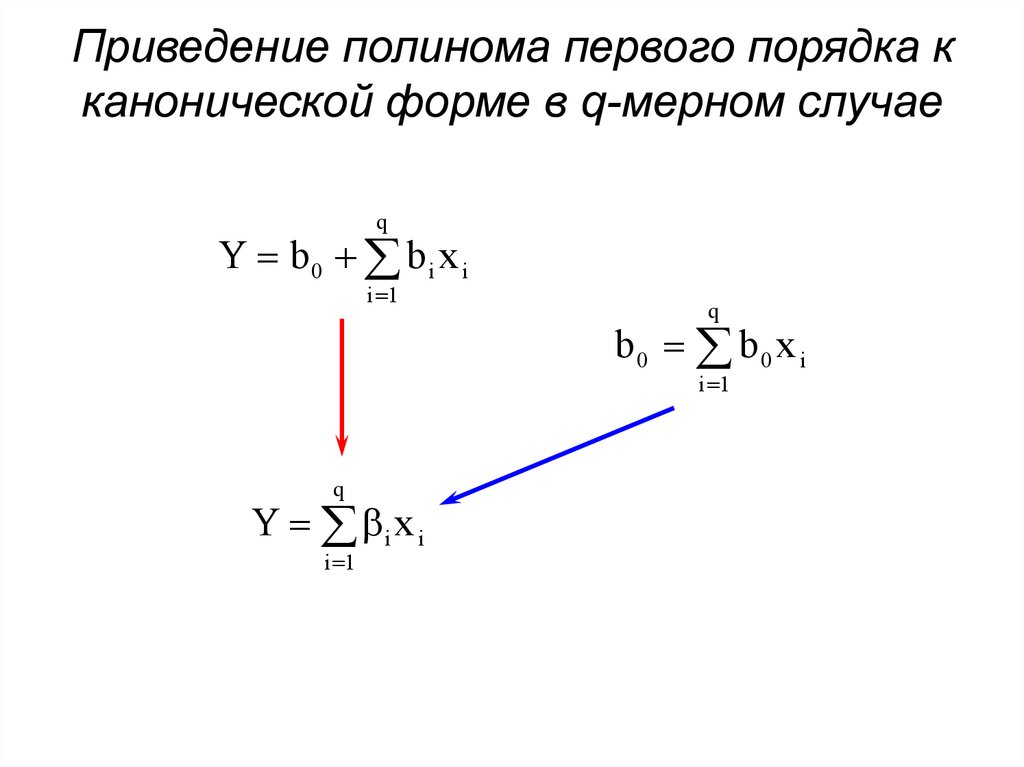
45. Приведение полинома первого порядка к канонической форме в q-мерном случае

q
Y b0 bi x i
i 1
q
b0 b0 x i
i 1
q
Y i x i
i 1

46. Приведение полинома второго порядка к канонической форме в q-мерном случае

k
k
k
i 1
i 1
i 1
Y b0 bi x i bijx i x j bii x i2
q
b0 b0 x i
i 1
q
x xi xix j
2
i
q
q
i 1
i 1
Y i x i ij x i x j
i 1

47. Приведение полинома третьего порядка к канонической форме в q-мерном случае

q
q
q
q
i 1
i 1
q
i 1
q
i 1
Y b0 bi x i bijx i x j bii x i2 biii x 3i
q
bijk x i x jx k biijx i2 x j bijjx i x 2j
i 1
i 1
i 1
q
b0 b0 x i
i 1
q
x xi xix j
2
i
i 1
q
1 q
x x i 3x i x j x i x j x i x j x i x j x k
2 i 1
i 1
q
1
2
x i x j x i x j x i x j x i x j x i x j x k
2 q
i 1
q
q
q
Y i x i ij x i x j ij x i x j x i x j b ijk x i x j x k
3
i
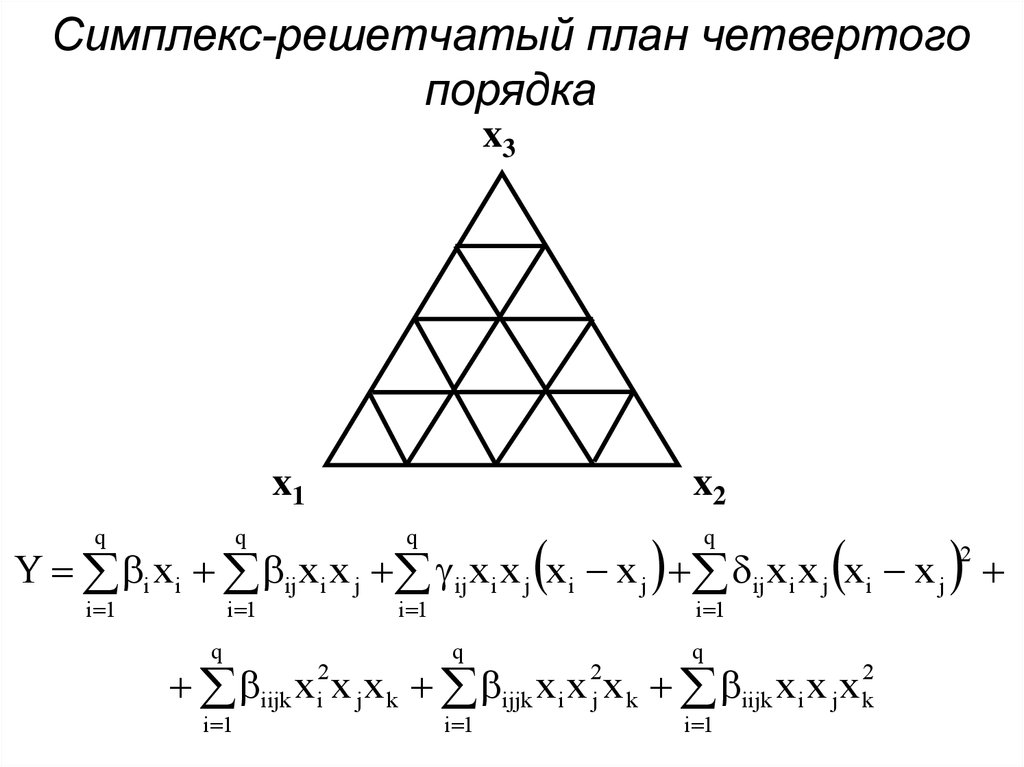
i 1
i 1
i 1
i 1

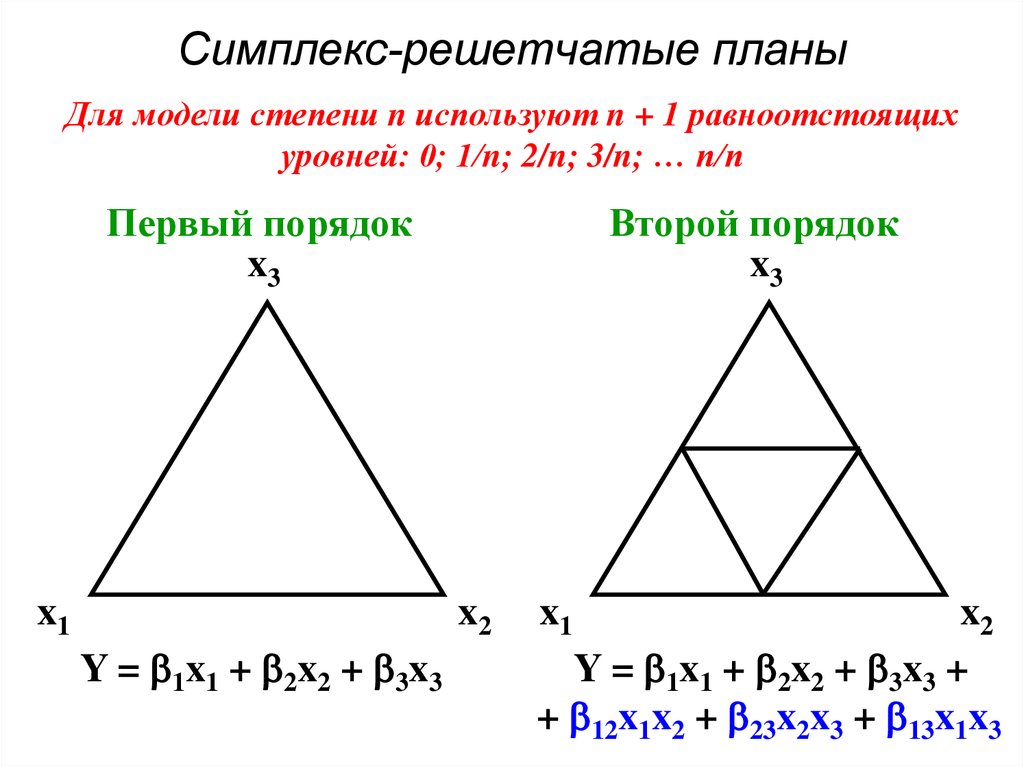
48. Симплекс-решетчатые планы

Для модели степени n используют n + 1 равноотстоящих
уровней: 0; 1/n; 2/n; 3/n; … n/n
Первый порядок
x3
x1
Второй порядок
x3
x2
Y = 1x1 + 2x2 + 3x3
x1
x2
Y = 1x1 + 2x2 + 3x3 +
+ 12x1x2 + 23x2x3 + 13x1x3

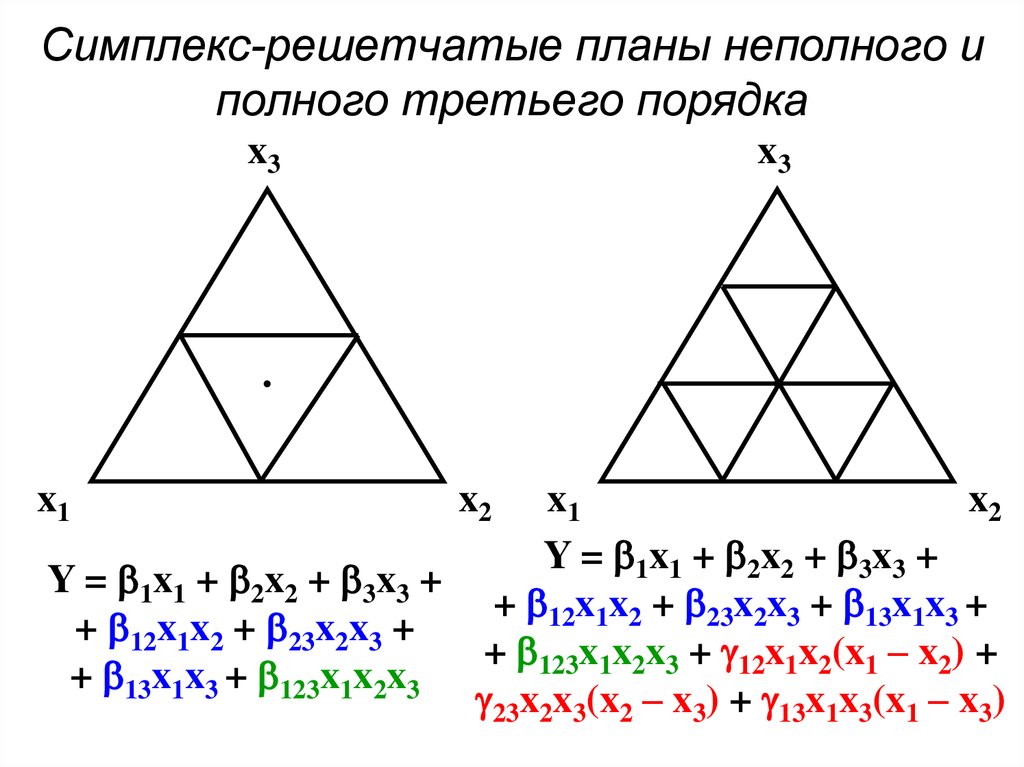
49. Симплекс-решетчатые планы неполного и полного третьего порядка

x3
x1
x3
x2
x1
x2
Y = 1x1 + 2x2 + 3x3 +
Y = 1x1 + 2x2 + 3x3 +
+ 12x1x2 + 23x2x3 + 13x1x3 +
+ 12x1x2 + 23x2x3 +
+ 123x1x2x3 + 12x1x2(x1 – x2) +
+ 13x1x3 + 123x1x2x3
23x2x3(x2 – x3) + 13x1x3(x1 – x3)

50. Симплекс-решетчатый план четвертого порядка

x3
x1
x2
Y i x i ijx i x j ijx i x j x i x j ijx i x j x i x j
q
q
q
q
i 1
i 1
i 1
i 1
q
q
q
i 1
i 1
i 1
iijk x i2 x jx k ijjk x i x 2j x k iijk x i x jx 2k
2

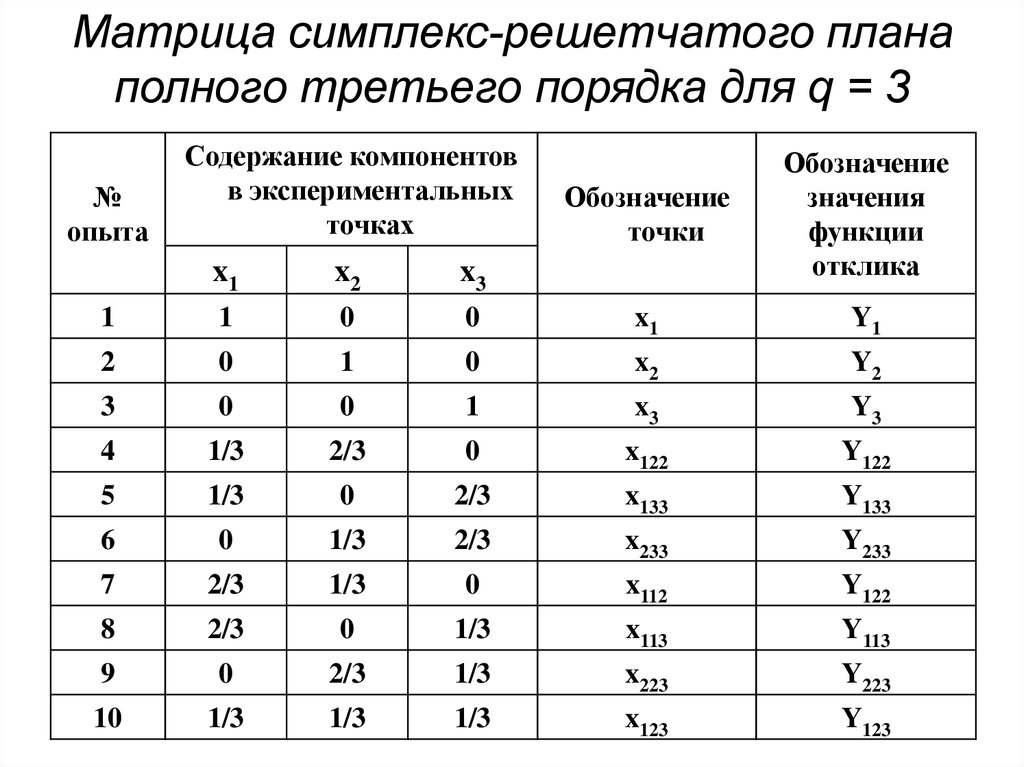
51. Матрица симплекс-решетчатого плана полного третьего порядка для q = 3

№
опыта
Содержание компонентов
в экспериментальных
точках
Обозначение
точки
Обозначение
значения
функции
отклика
x1
x2
x3
1
1
0
0
x1
Y1
2
0
1
0
x2
Y2
3
0
0
1
x3
Y3
4
1/3
2/3
0
x122
Y122
5
1/3
0
2/3
x133
Y133
6
0
1/3
2/3
x233
Y233
7
2/3
1/3
0
x112
Y122
8
2/3
0
1/3
x113
Y113
9
0
2/3
1/3
x223
Y223
10
1/3
1/3
1/3
x123
Y123

52. Расчет коэффициентов уравнения регрессии методом подстановки (1)

На примере уравнения для симплекс-решетчатого
плана второго порядка
Y = 1x1 + 2x2 + 3x3 + 12x1x2 + 23x2x3 + 13x1x3
Для точки с координатами x1 = 1; x2 = 0; x3 = 0
Y1 = 1 1 + 2 0 + 3 0 + 12 1 0 + 23 0 0 + 13 1 0 = 1
Аналогично
2 =Y2
3 =Y3
i =Yi

53. Расчет коэффициентов уравнения регрессии методом подстановки (2)

Для точки с координатами x1 = 1/2; x2 = 1/2; x3 = 0
Y12 = 1 1/2 + 2 1/2 + 3 0 + 12 1/2 1/2 + 23 1/2 0 +
+ 13 1/2 0 = 1 1/2 + 2 1/2 + 12 1/4
С учетом i =Yi
12 = 4Y12 – 2Y1 – 2Y2
Аналогично
23 = 4Y23 – 2Y2 – 2Y3
13 = 4Y13 – 2Y1 – 2Y3
ij = 4Yij – 2Yi – 2Yj

54. Расчет коэффициентов уравнения регрессии для плана неполного третьего порядка

i =Yi
ij = 4Yij – 2Yi – 2Yj
123 = 27Y123 – 12(Y12 + Y23 + Y13) +
+ 3(Y1 + Y2 + Y3)

55. Расчет коэффициентов уравнения регрессии для плана полного третьего порядка

i =Yi
ij = 9/4 (Yiij + Yijj– Yi – Yj)
123 = 27Y123 – 27/4 (Y112 + Y122 + Y223 +
+ Y233 + Y113 + Y133) + 9/2 (Y1 + Y2 + Y3)
ij = 9/4 (3Yiij – 3Yijj– Yi + Yj)

56. Проверка адекватности уравнения регрессии по критерию Сьюдента (1)

tрасч tтабл для всех контрольных точек
t расч
Yr Yrp
S( Y Y
r
rp
S( Y Y ) S2Y S2Y
r
rp
r
)
Yr – экспериментальное (среднее) значение в контрольной
точке r
Yrр – расчетное значение в контрольной точке r
Sy2 – средняя дисперсия опытов в основных точках плана
Syr2 – средняя дисперсия опытов в контрольных точках плана

57. Проверка адекватности уравнения регрессии по критерию Сьюдента (2)

t расч
Yr Yrp
S S
2
Y
2
Yr
t расч
Yr Yrp n r *
SY 1
* - по данным Шеффе и Микешиной
nr – число дублирований опыта в контрольной точке r
– величина, зависящая от положения контрольной точки на
симплексе

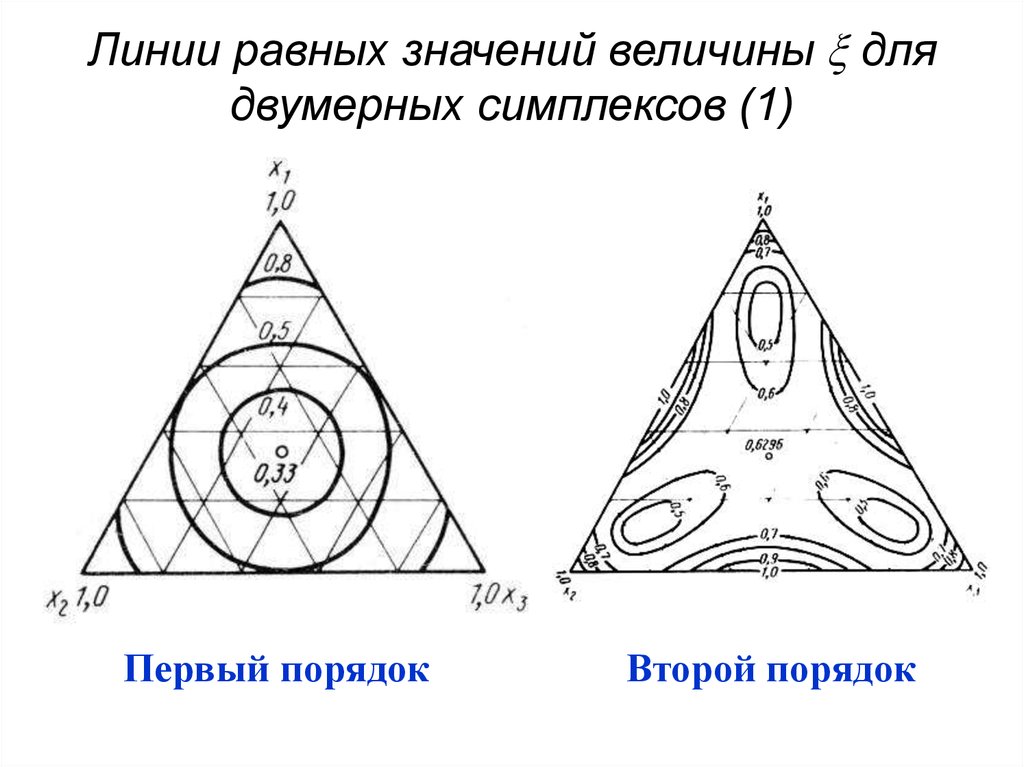
58. Линии равных значений величины  для двумерных симплексов (1)

Линии равных значений величины для
двумерных симплексов (1)
Первый порядок
Второй порядок

59. Линии равных значений величины  для двумерных симплексов (2)

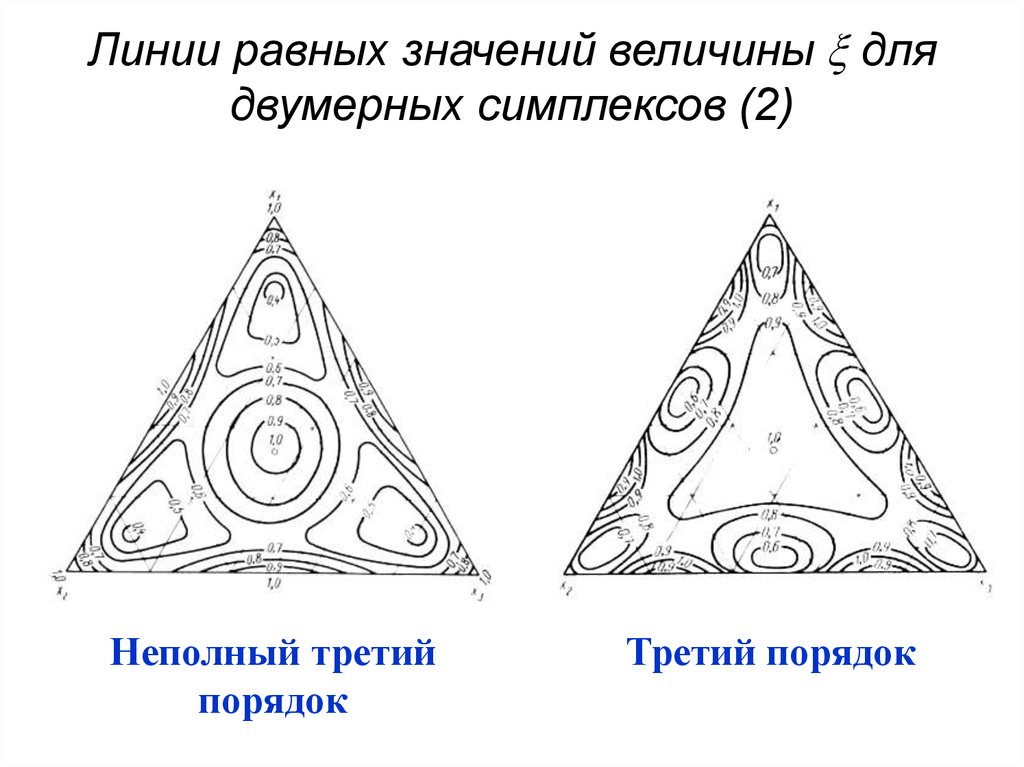
Линии равных значений величины для
двумерных симплексов (2)
Неполный третий
порядок
Третий порядок

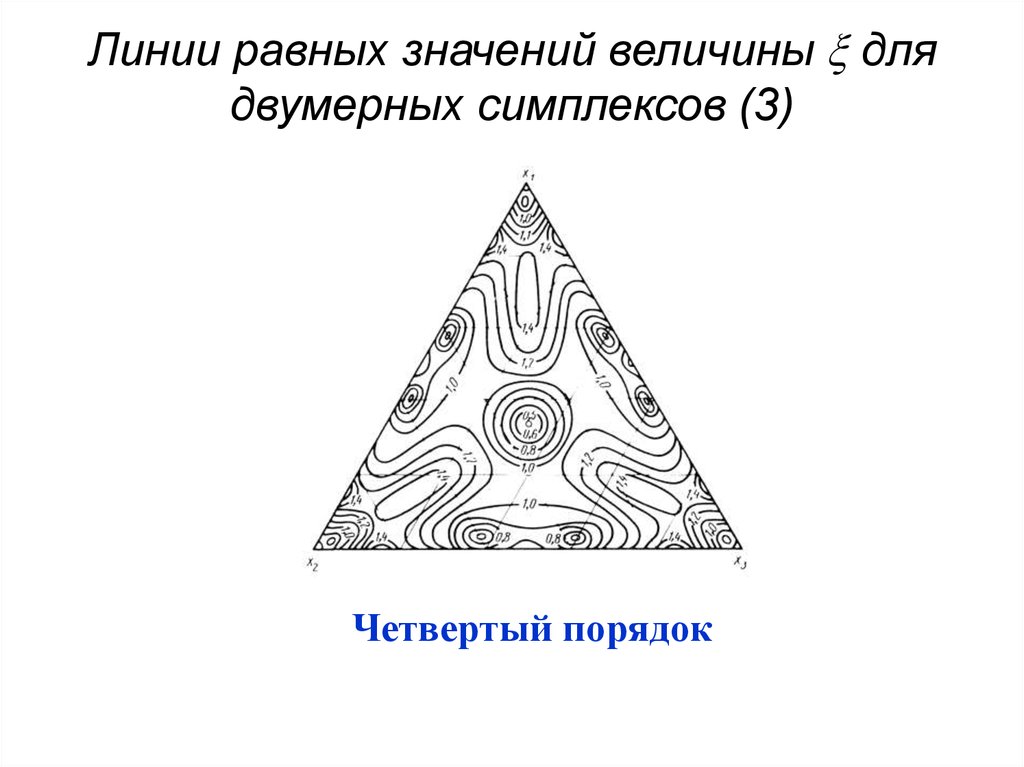
60. Линии равных значений величины  для двумерных симплексов (3)

Линии равных значений величины для
двумерных симплексов (3)
Четвертый порядок

61. Расчет значений  (1)

Расчет значений (1)
Модель первого порядка
q
x i2
i 1
Модель второго порядка
x i 2x i 1 4x i x j
q
q
2
i 1
i 1
Модель неполного третьего порядка
2
2
2
0,5x i 6x i 2x i 1 3 x j
i 1
j 1
q
q
4x i x j 3x i 3x j 2 27 x i x jx k
q
i 1
2
q
i 1
2
2

62. Расчет значений  (2)

Расчет значений (2)
Модель третьего порядка
2
0,5x i 3x i 1 3x i 2 4,5x i x j 3x i 1
q
q
2
i 1
i 1
4,5x i x j 3x j 1 2 27 x i x jx k 2
q
q
i 1
i 1

63. Оценка дисперсии значений, предсказанных моделью (1)

На примере уравнения для плана второго порядка
Yрасч = Y1x1 + Y2x2 + Y3x3 + (4Y12 – 2Y1 – 2Y2)x1x2 +
+ (4Y23 – 2Y2 – 2Y3)x2x3 + (4Y13 – 2Y1 – 2Y3)x1x3
Yрасч = Y1(x1 – 2x1x2 – 2x1x3) + Y2(x2 – 2x1x2 – 2x2x3) +
+ Y3(x3 – 2x1x3 – 2x2x3) + 4Y12x1x2 + 4Y23x2x3 + 4Y13x1x3
Yрасч = x1(2x1 – 1)Y1 + x2(2x2 – 1)Y2 + x3(2x3 – 1)Y3 +
+ 4x1x2Y12 + 4x2x3Y23 + 4x1x3Y13

64. Оценка дисперсии значений, предсказанных моделью (2)

q
q
i 1
i 1
Yрасч b i Yi b ij Yij
bi = xi(2xi – 1)
bij = 4xixj
Если величины xi определяются без ошибок
q
q
S2Yp b i2S2Y b ij2S2Y
2
S
S2Y Y
ni
2
S
2
SY Y
n ij
i
i 1
i
ij
S2Yp
i 1
ij
2
q
q b2
bi
ij
2
SY
i 1 n i i 1 n ij

65. Оценка дисперсии значений, предсказанных моделью (3)

При равномерном дублировании ni = nij = n
S
2
Yp
S
n
2
Y
t S
t SY
2
Yp
SY
t
n
n
–доверительный интервал значений функции
отклика, предсказываемых моделью

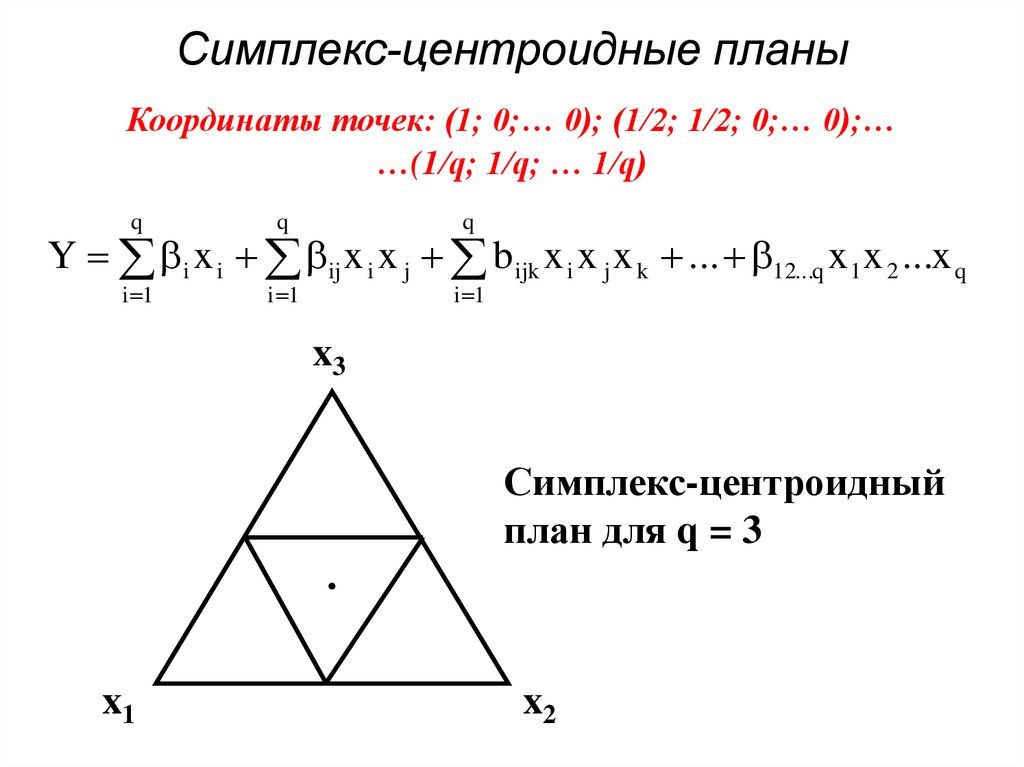
66. Симплекс-центроидные планы

Координаты точек: (1; 0;… 0); (1/2; 1/2; 0;… 0);…
…(1/q; 1/q; … 1/q)
q
q
q
i 1
i 1
i 1
Y i x i ij x i x j b ijk x i x j x k ... 12...q x 1 x 2 ...x q
x3
Симплекс-центроидный
план для q = 3
x1
x2

67. D-оптимальные планы

Координаты точек модели третьего порядка для q факторов:
(1; 0;… 0); (0,7236; 0,2764; 0;… 0); (1/3; 1/3; 1/3; 0;… 0)
Координаты точек модели четвертого порядка для q
факторов: (1; 0;… 0); (1/2; 1/2; 0;… 0); (0,8273; 0,1727; 0;… 0);
(0,5670; 0,2165; 0,2165; 0;… 0); (1/4; 1/4; 1/4; 1/4; 0;… 0)

68. Матрица D-оптимального плана третьего порядка для q = 3

№
опыта
Содержание компонентов в
экспериментальных точках
Обозначение
точки
Обозначение
значения функции
отклика
x1
x2
x3
1
1
0
0
x1
Y1
2
0
1
0
x2
Y2
3
0
0
1
x3
Y3
4
0,2764
0,7236
0
x122
Y122
5
0,2764
0
0,7236
x133
Y133
6
0
0,2764
0,7236
x233
Y233
7
0,7236
0,2764
0
x112
Y122
8
0,7236
0
0,2764
x113
Y113
9
0
0,7236
0,2764
x223
Y223
10
1/3
1/3
1/3
x123
Y123

69. Расчет коэффициентов уравнения регрессии для D-оптимального плана третьего порядка

i =Yi
ij = 2,5 (Yiij + Yijj– Yi – Yj)
123 = 27Y123 – 7,5 (Y112 + Y122 + Y223 +
+ Y233 + Y113 + Y133) + 6 (Y1 + Y2 + Y3)
ij = 2,5 (Yi – Yj) + 2,5·50,5 (Yiij – Yijj)

70. Поиск экстремума методом последовательного симплекс-планирования

x2
Движение симплексов по
линии, близкой к линии
градиента
1
8
x1

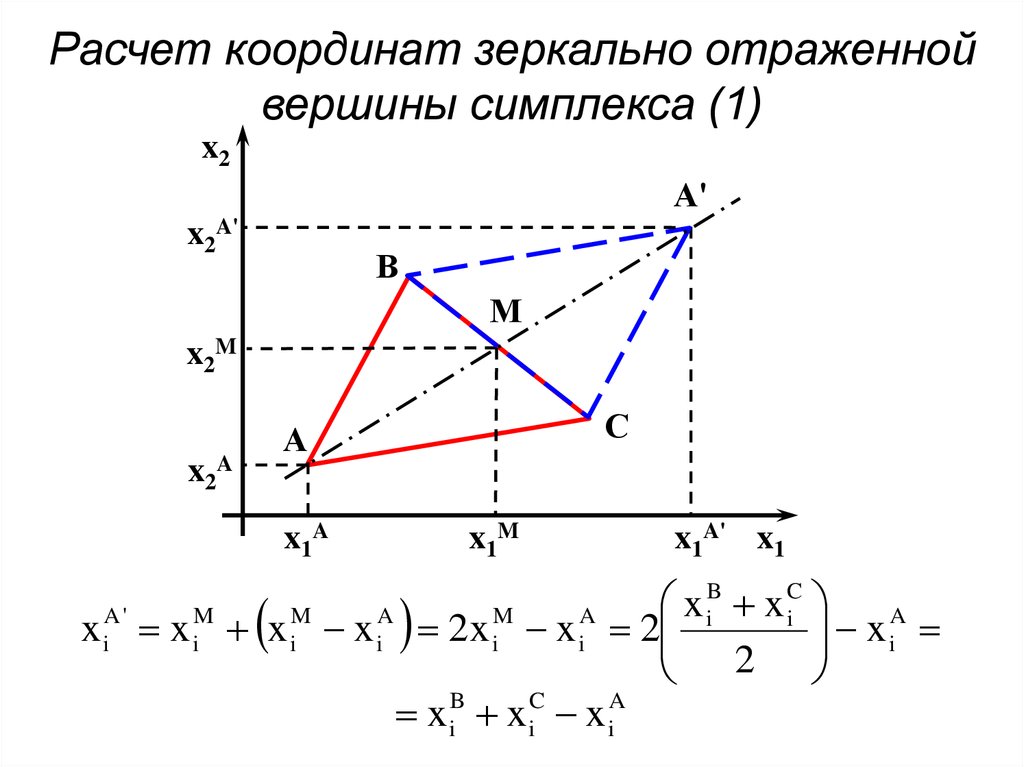
71. Расчет координат зеркально отраженной вершины симплекса (1)

x2
А'
x2A'
В
М
x2M
x2A
С
А
x1A
x1M
x1A' x1
B
C
x
x
A'
M
M
A
M
A
i
i
x iA
x i x i x i x i 2x i x i 2
2
x iB x iC x iA

72. Расчет координат зеркально отраженной вершины симплекса (2)

2 1
x x i x i2 ... x if 1 x if 1 ... x iq 1 x if
q
*
i
i – номер фактора
q –число факторов
* – индекс новой (зеркальной) вершины
f – индекс вершины с наихудшим значением отклика
1; 2; (f – 1); (f + 1) – индексы остальных вершин симплекса

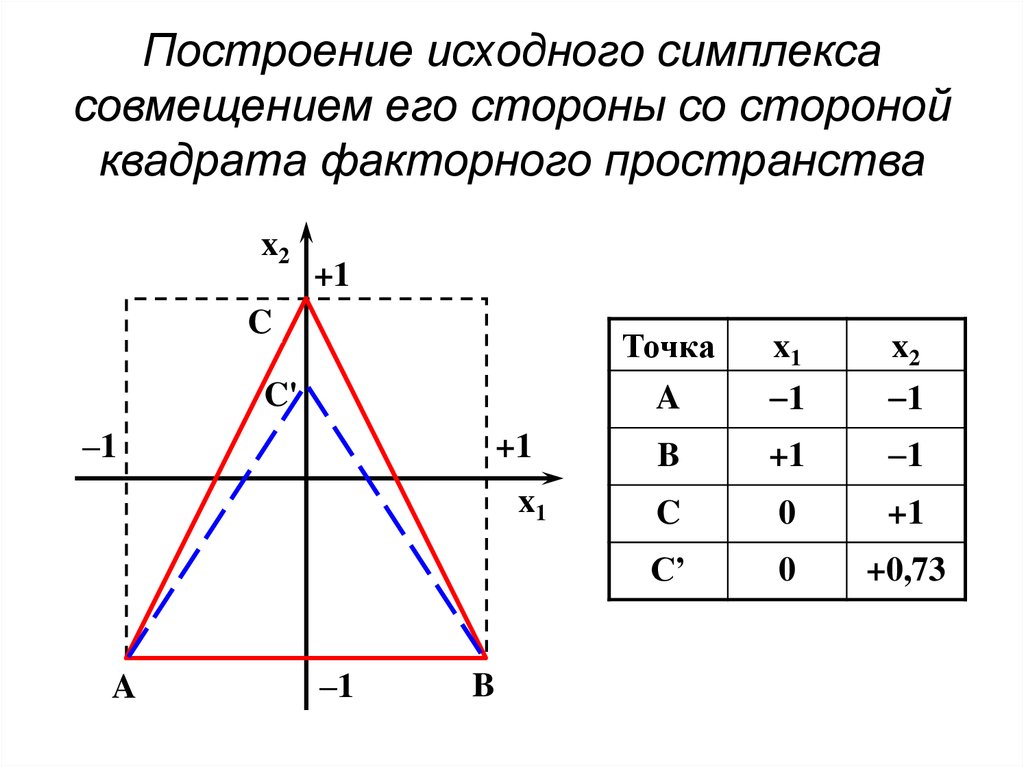
73. Построение исходного симплекса совмещением его стороны со стороной квадрата факторного пространства

x2
+1
C
C'
–1
+1
x1
A
–1
B
Точка
x1
x2
A
1
1
B
+1
1
C
0
+1
C’
0
+0,73

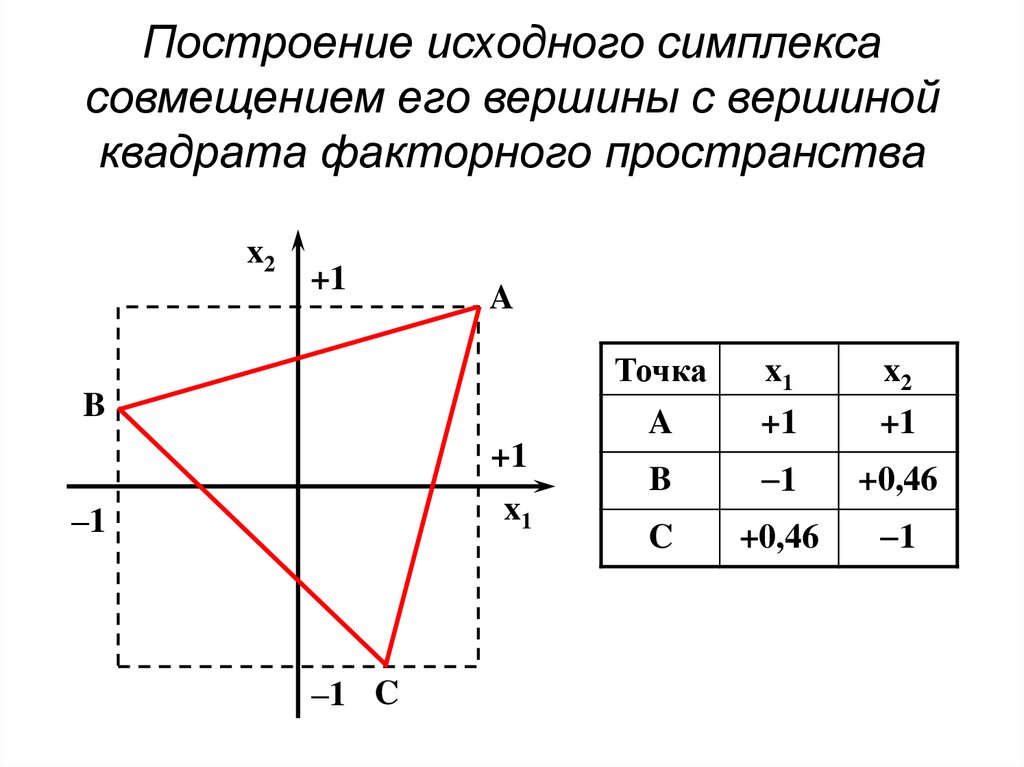
74. Построение исходного симплекса совмещением его вершины с вершиной квадрата факторного пространства

x2
+1
A
B
+1
x1
–1
–1 C
Точка
x1
x2
A
+1
+1
B
1
+0,46
C
+0,46
1

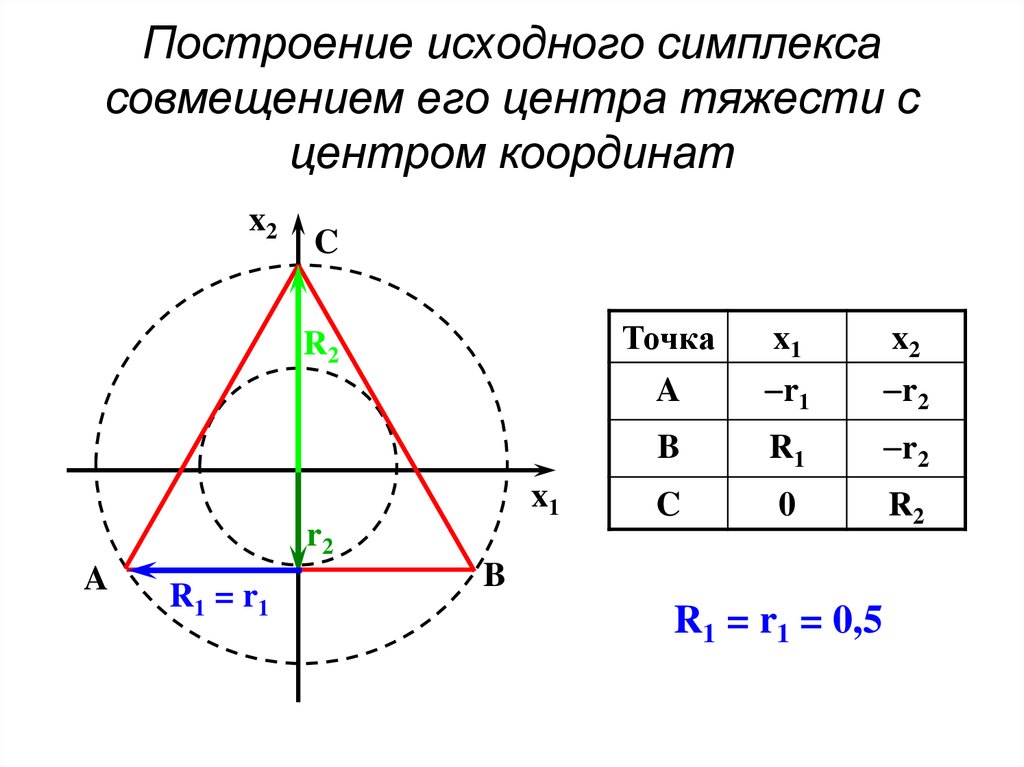
75. Построение исходного симплекса совмещением его центра тяжести с центром координат

x2
C
R2
x1
r2
A
R1 = r1
Точка
x1
x2
A
r1
r2
B
R1
r2
C
0
R2
B
R1 = r1 = 0,5

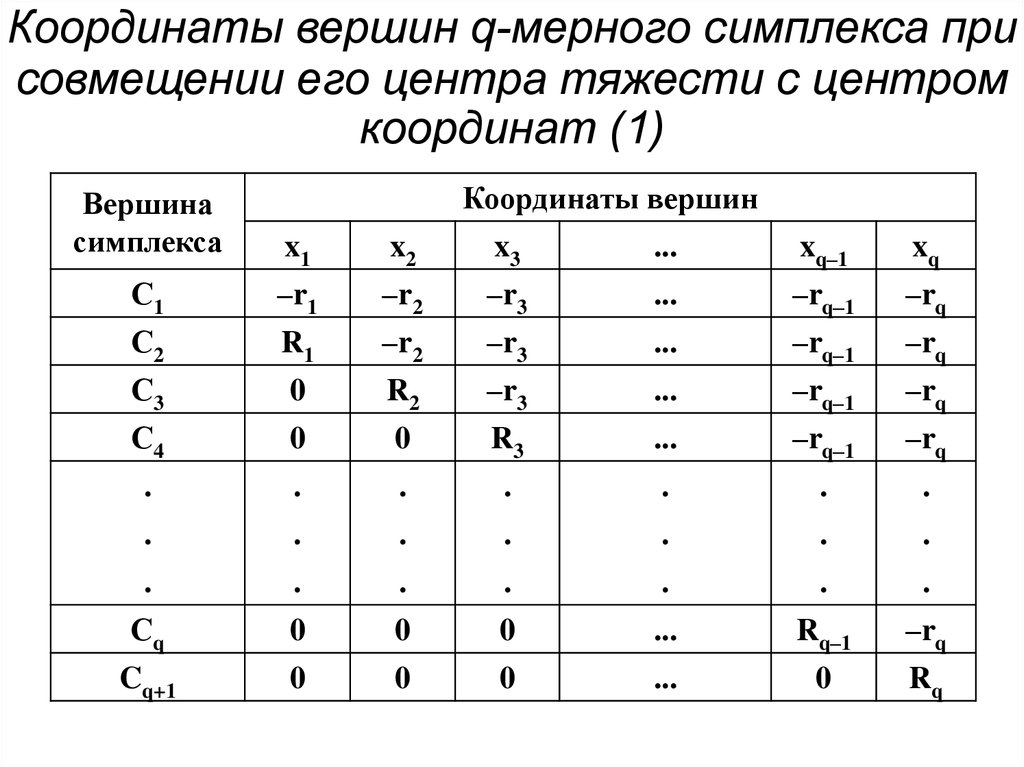
76. Координаты вершин q-мерного симплекса при совмещении его центра тяжести с центром координат (1)

Координаты вершин
Вершина
симплекса
x1
x2
x3
...
xq–1
xq
С1
–r1
–r2
–r3
...
–rq–1
–rq
С2
R1
–r2
–r3
...
–rq–1
–rq
С3
0
R2
–r3
...
–rq–1
–rq
С4
0
0
R3
...
–rq–1
–rq
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Сq
0
0
0
...
Rq–1
–rq
Cq+1
0
0
0
...
0
Rq

77. Координаты вершин q-мерного симплекса при совмещении его центра тяжести с центром координат (2)

При длине ребра i-мерного (1 i < q) симплекса, равной 1
1
ri
2i i 1
i
Ri
2 i 1
Для двумерного симплекса
r2
1
0,289
2 2 2 1
2
R2
0,578
2 2 1

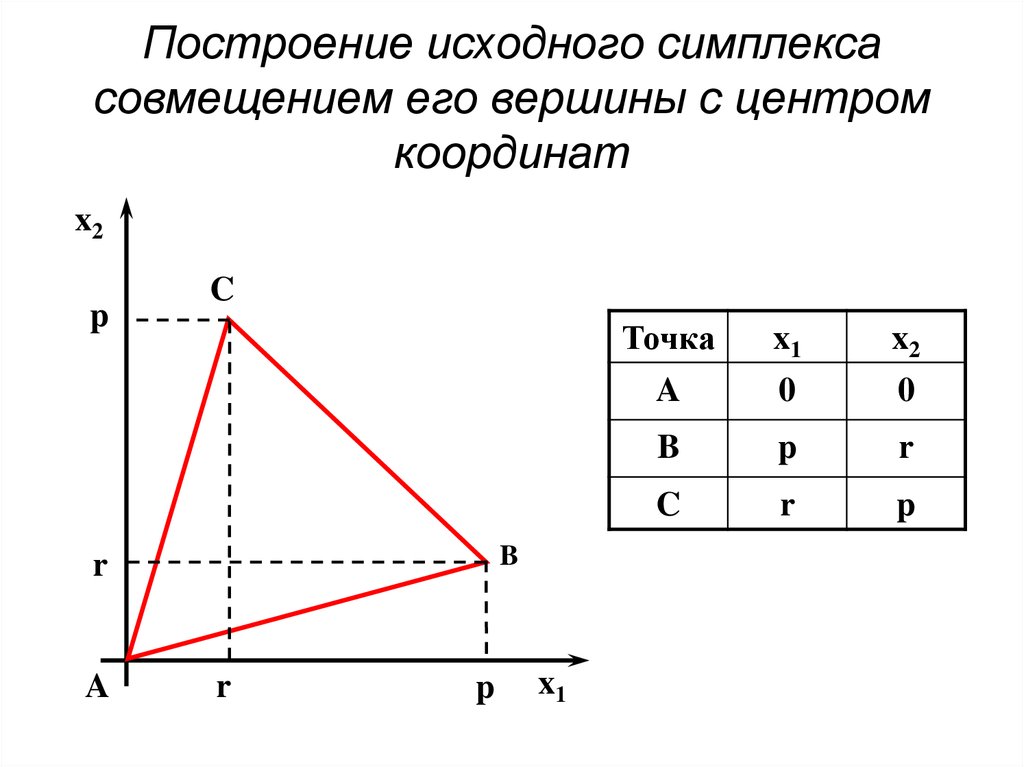
78. Построение исходного симплекса совмещением его вершины с центром координат

x2
p
C
B
r
A
r
p
x1
Точка
x1
x2
A
0
0
B
p
r
C
r
p

79. Координаты вершин q-мерного симплекса при совмещении его вершины с центром координат (1)

Координаты вершин
Вершина
симплекса
x1
x2
x3
...
xq–1
xq
С1
0
0
0
...
0
0
С2
p
r
r
...
r
r
С3
r
p
r
...
r
r
С4
r
r
p
...
r
r
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Сq
r
r
r
...
p
r
Cq+1
r
r
r
...
r
p

80. Координаты вершин q-мерного симплекса при совмещении его вершины с центром координат (2)

p
1
q
q 1
2
q 1
r
1
q
2
При q = 2
p
1
2
r
2 1
2
1
2
2
2 1 0,966
2 1 1 0,259
q 1 1

81. Качание симплекса относительно одной грани

С10
С8
С8
С9
С9
С7
С7
С11

82. Метод деформированного симплекса

2 1
x x i x i2 ... x if 1 x if 1 ... x iq 1 x if
q
*
i
где:
xi
x
x *i 2x i x if
1
i
x i2 ... x if 1 x if 1 ... x iq 1
q
x*i x if 2 x i x if x if 1 x i x if
– коэффициент деформации симплекса
= – нормальное отражение
= – сжатие симплекса
= – растяжение симплекса

83. Виды деформации двумерного симплекса

x2
4 – нормальное отражение
5 – растяжение симплекса
5
4
2
6
7
1
3
6 – положительное сжатие
7 – отрицательное сжатие
x1

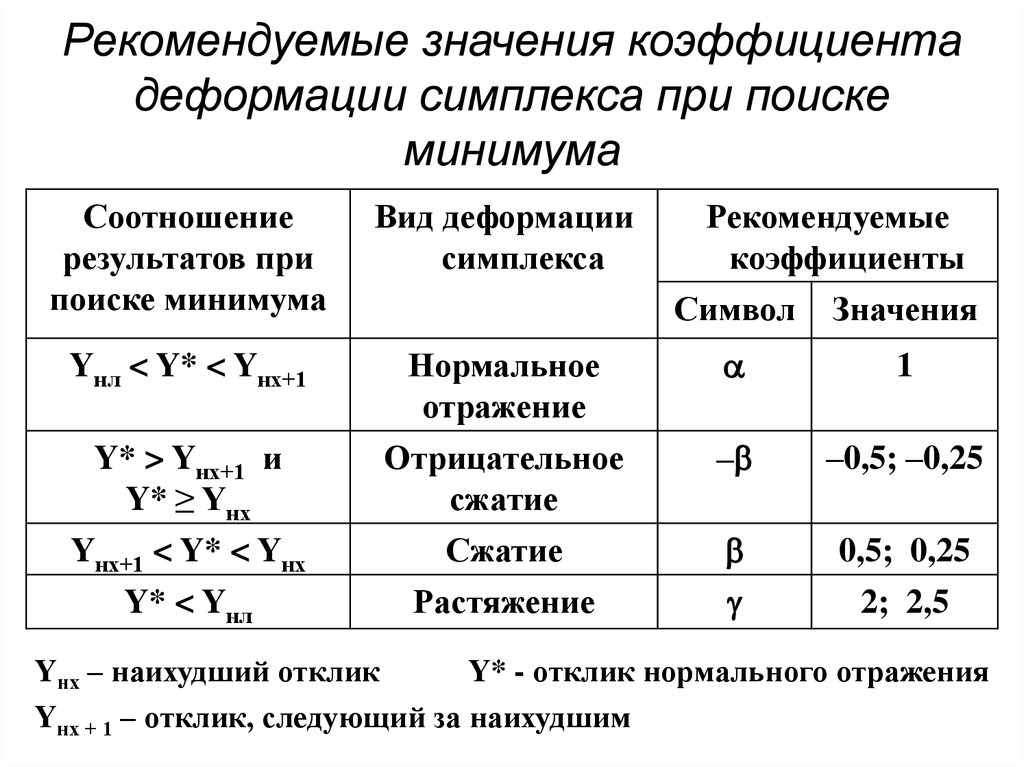
84. Рекомендуемые значения коэффициента деформации симплекса при поиске минимума

Соотношение
результатов при
поиске минимума
Вид деформации
симплекса
Yнл < Y* < Yнх+1
Нормальное
отражение
Отрицательное
сжатие
Сжатие
Растяжение
Y* > Yнх+1 и
Y* ≥ Yнх
Yнх+1 < Y* < Yнх
Y* < Yнл
Рекомендуемые
коэффициенты
Символ Значения
1
–
–0,5; –0,25
0,5; 0,25
2; 2,5
Yнх – наихудший отклик
Y* - отклик нормального отражения
Yнх + 1 – отклик, следующий за наихудшим

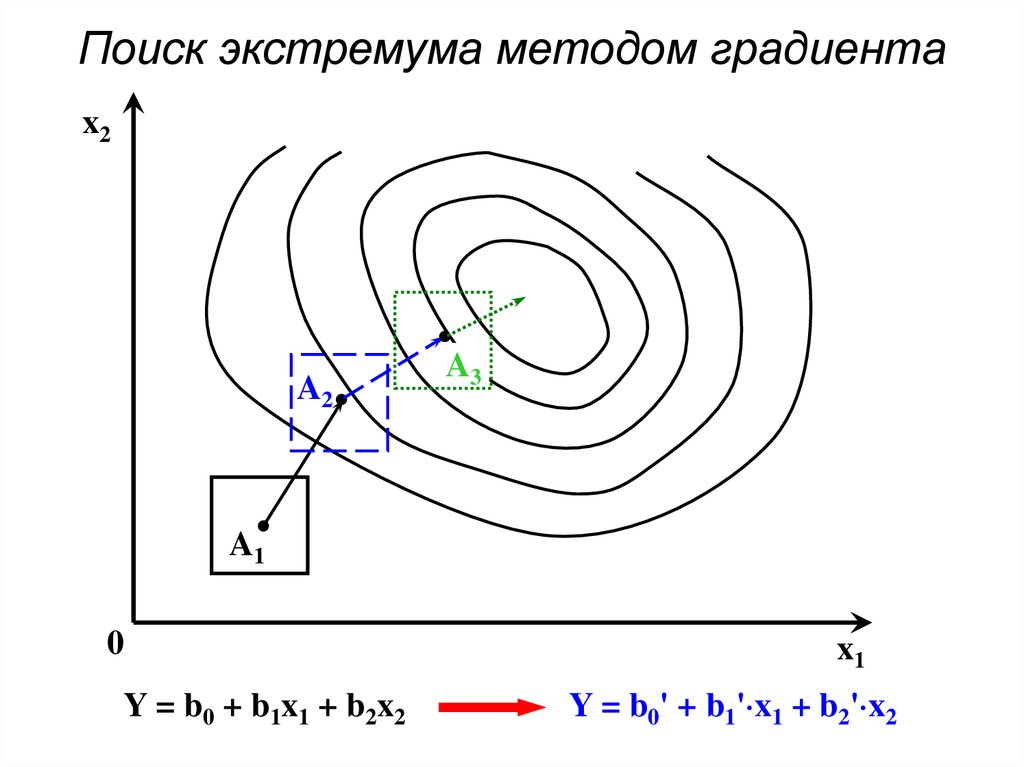
85. Поиск экстремума методом градиента

x2
A2
A3
A1
0
Y = b0 + b1x1 + b2x2
x1
Y = b0' + b1' x1 + b2' x2

86. Использование компонентов градиента при переходе на следующий уровень функции отклика

Y = b0 + b1x1 + b2x2
b1 < b2
B
C
x2
x2
Y + Y
b1
b2
A
0
x1
D
x1
Y

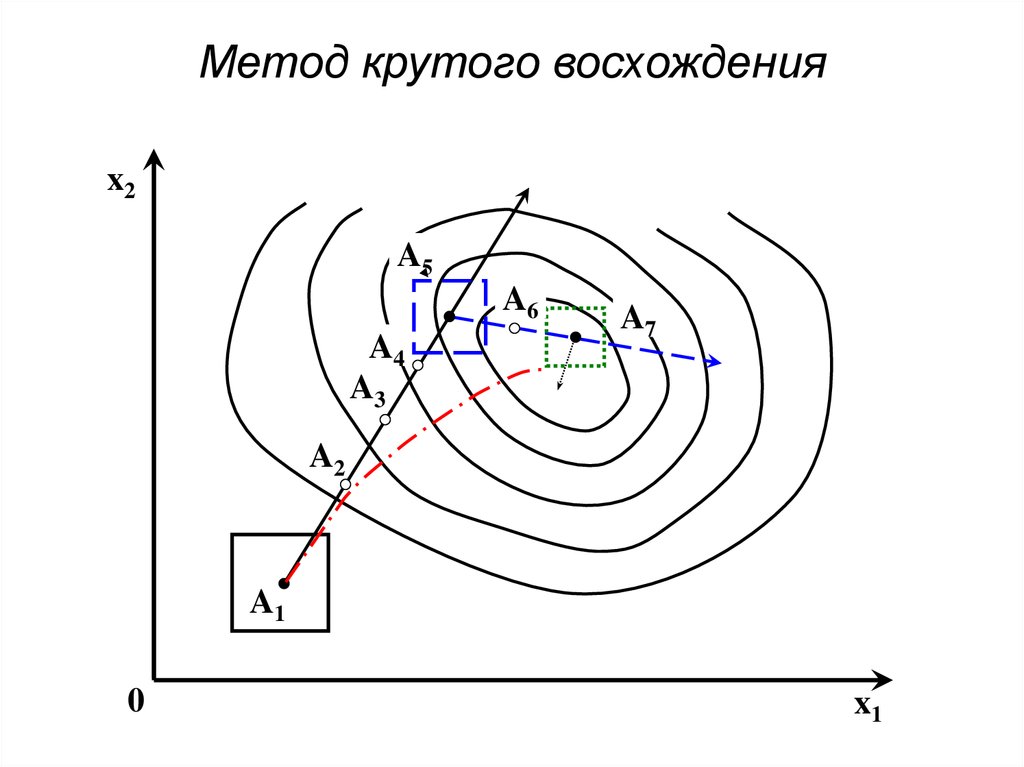
87. Метод крутого восхождения

x2
A5
A6
A4
A3
A7
A2
A1
0
x1

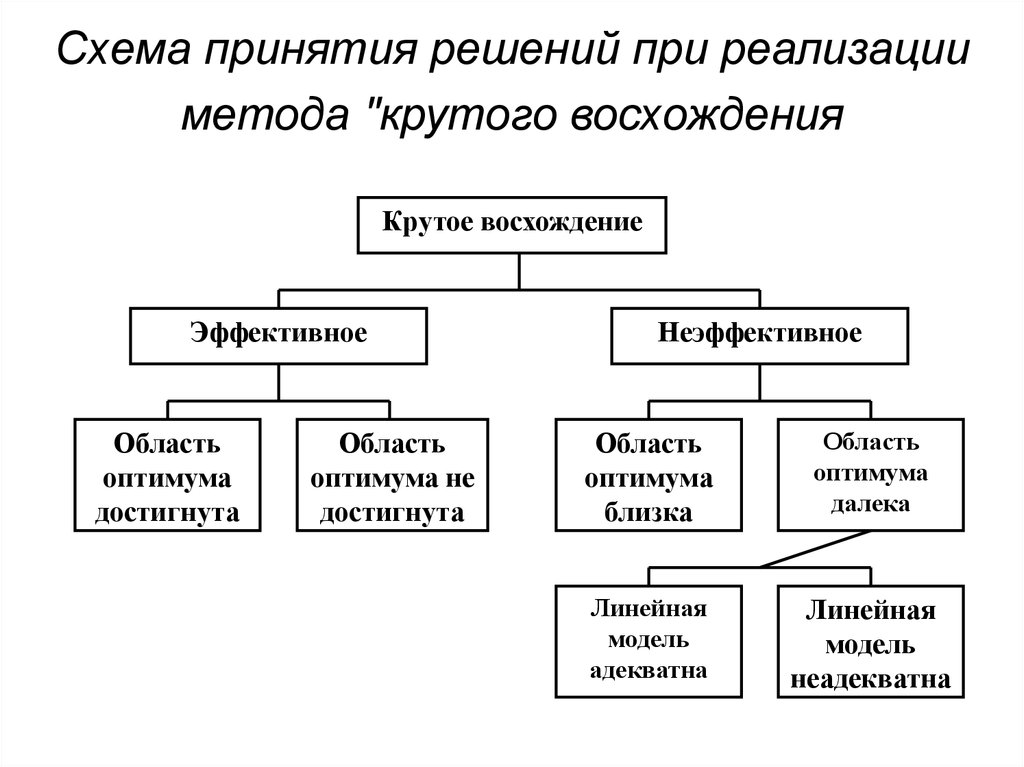
88. Схема принятия решений при реализации метода "крутого восхождения

Схема принятия решений при реализации
метода "крутого восхождения
Крутое восхождение
Эффективное
Область
оптимума
достигнута
Область
оптимума не
достигнута
Неэффективное
Область
оптимума
близка
Область
оптимума
далека
Линейная
модель
адекватна
Линейная
модель
неадекватна

89. Обобщенный параметр оптимизации

m
Yi y ui
u 1
m
Yi m y ui
u 1
Yi – обобщенный параметр оптимизации для i-го опыта
yui – значение частного отклика yu в i-м опыте
i = 1, 2, …, N;
u = 1, 2, …, m

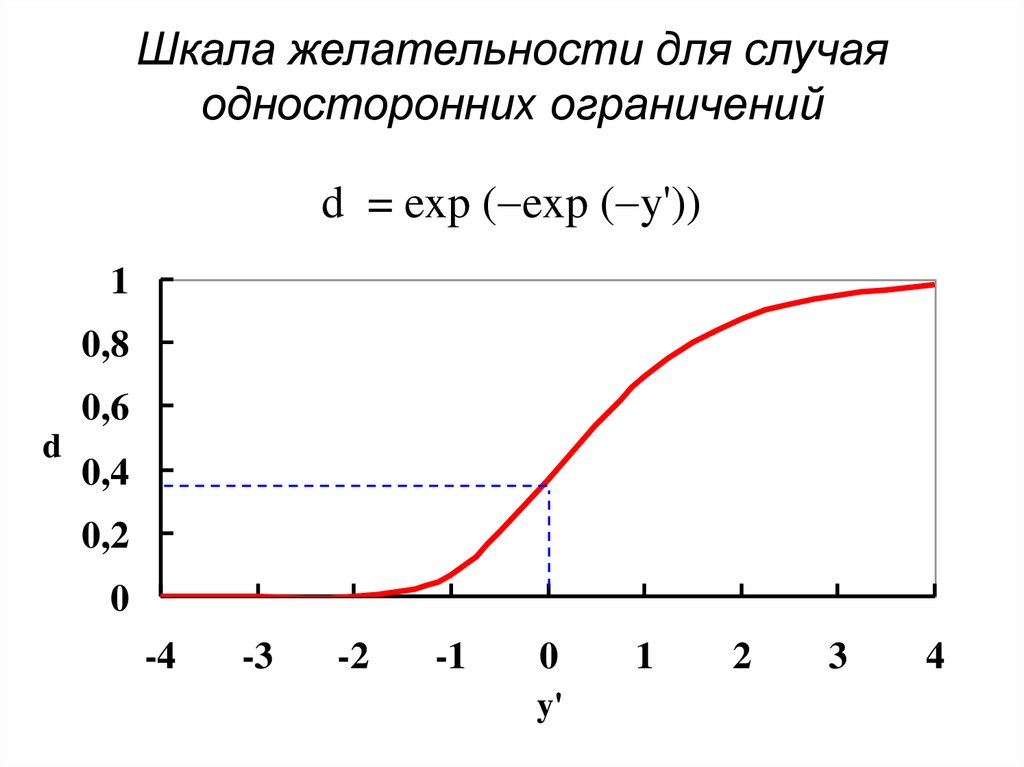
90. Шкала желательности для случая односторонних ограничений

d = exp ( exp ( y'))
1
0,8
0,6
d
0,4
0,2
0
-4
-3
-2
-1
0
y'
1
2
3
4

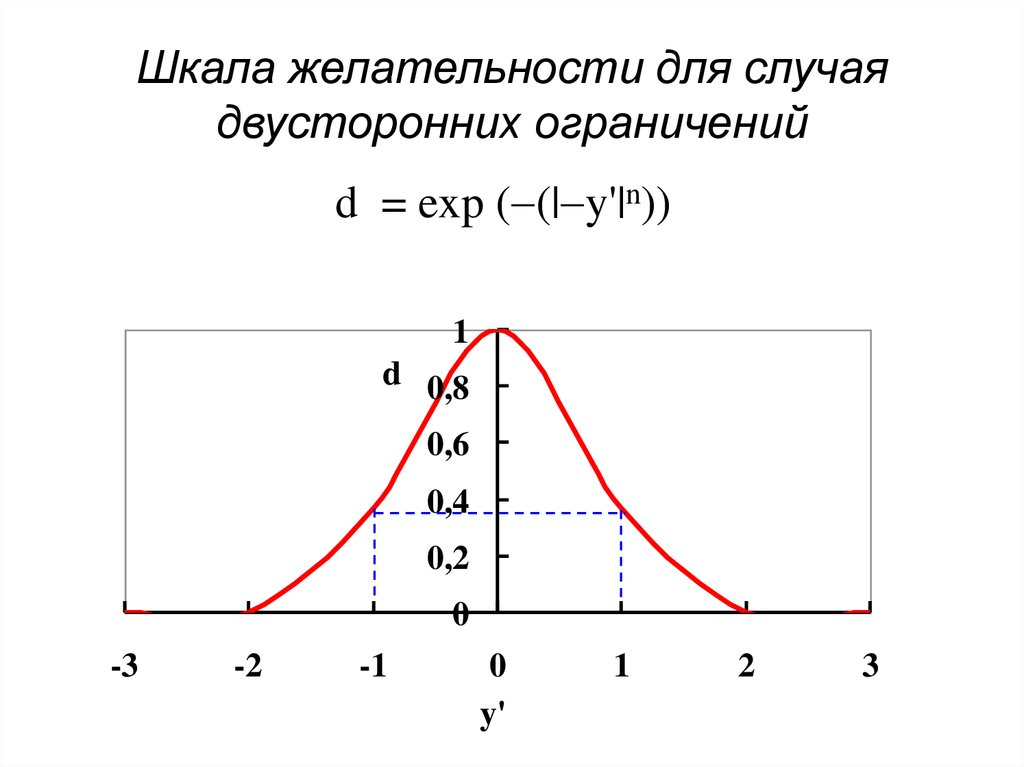
91. Шкала желательности для случая двусторонних ограничений

d = exp ( (| y'|n))
1
d 0,8
0,6
0,4
0,2
0
-3
-2
-1
0
y'
1
2
3