Аппроксимация методом наименьших квадратов (МНК)

1. Аппроксимация методом наименьших квадратов (МНК)

Мелехин Александр Алексеевич
преподаватель кафедры Е1

2. Что это такое?

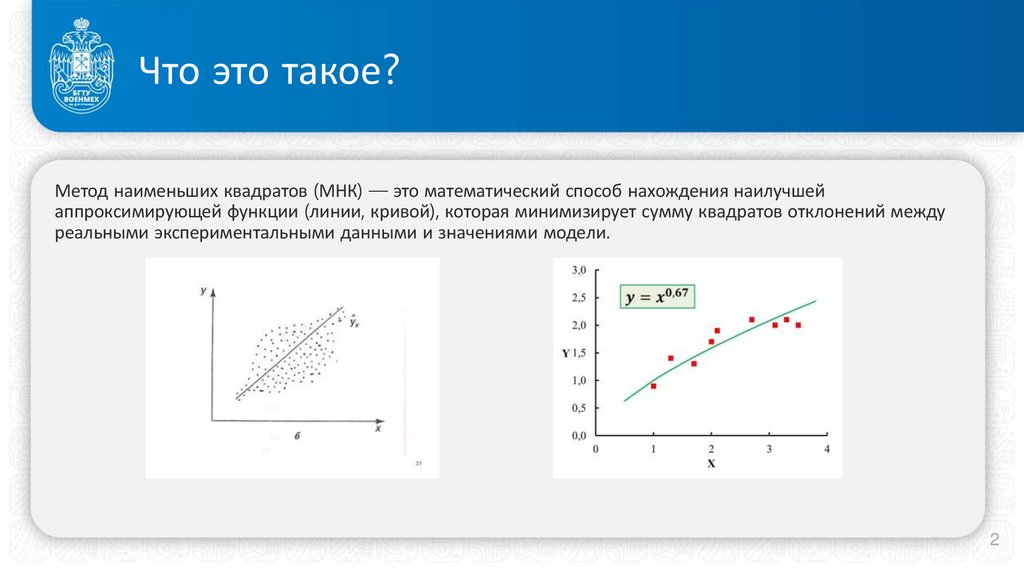
Метод наименьших квадратов (МНК) — это математический способ нахождения наилучшей
аппроксимирующей функции (линии, кривой), которая минимизирует сумму квадратов отклонений между
реальными экспериментальными данными и значениями модели.
2

3. Когда целесообразно использовать МНК?

1. При наличии экспериментальных данных с шумами.
- В реальных измерениях всегда есть случайные ошибки (например, из-за неточности приборов).
- МНК помогает построить гладкую зависимость, убирая влияние случайных ошибок.
2. Для моделирования сложных зависимостей.
- Иногда аналитическая формула неизвестна, но есть набор точек (x, y).
- Аппроксимация помогает найти функцию, описывающую данные.
3. Для предсказания значений вне измеренного диапазона.
- Если функция хорошо аппроксимирует данные, ее можно использовать для прогнозирования.
4. В инженерии, экономике, науке и технике.
- Физика: анализ экспериментальных зависимостей (например, зависимость сопротивления от температуры).
- Экономика: прогнозирование спроса, цен и трендов.
- Машиностроение: подбор параметров технологических процессов.
3

4. Примеры использования МНК

- Прямая регрессия (линейная аппроксимация).
Например, зависимость расхода топлива от скорости тягача, буксирующего арт. орудие.
- Полиномиальная аппроксимация.
Для сложных нелинейных зависимостей (например, траектория снаряда).
- Экспоненциальные и логарифмические модели.
Для анализа роста популяции, радиоактивного распада, финансовых данных.
4

5. Разница между аппроксимацией, интерполяцией и экстраполяцией

Аппроксимация — научный метод, состоящий
в замене одних объектов другими, в каком-то
смысле близкими к исходным, но более
простыми. В математике это построение
кривых, близких к имеющемуся набору
значений.
Интерполяция — это нахождение неизвестных
промежуточных
значений
с
помощью
нескольких известных. Интерполировать —
это, по сути, вставить дополнительные
значения в ряд.
Экстраполяция — это метод нахождения
значений за пределами интервала. Разница с
интерполяцией в том, что неизвестные
данные ищутся не в промежутке, а за его
пределами.
Полезная ссылка:
https://blog.skillfactory.ru/approksimatsiyainterpolyatsiya-ekstrapolyatsiya/.
5

6. Выводы

Метод наименьших квадратов — мощный инструмент для обработки, анализа и прогнозирования данных,
особенно если наблюдения содержат шум или зависимость между переменными сложная.
6

7. Спасибо за внимание!