Похожие презентации:
Метод наименьших квадратов
1.
Метод наименьших квадратовМетод наименьших квадратов (МНК, OLS, Ordinary Least Squares)
— один из базовых методов анализа для оценки неизвестных
параметров моделей по выборочным данным.
Основной принцип метода: сумма квадратов ошибки модели
должна быть минимальной.
При построении моделей могут использоваться два
принципиально различных типа исходных
информационных массивов — статический и динамический.
2.
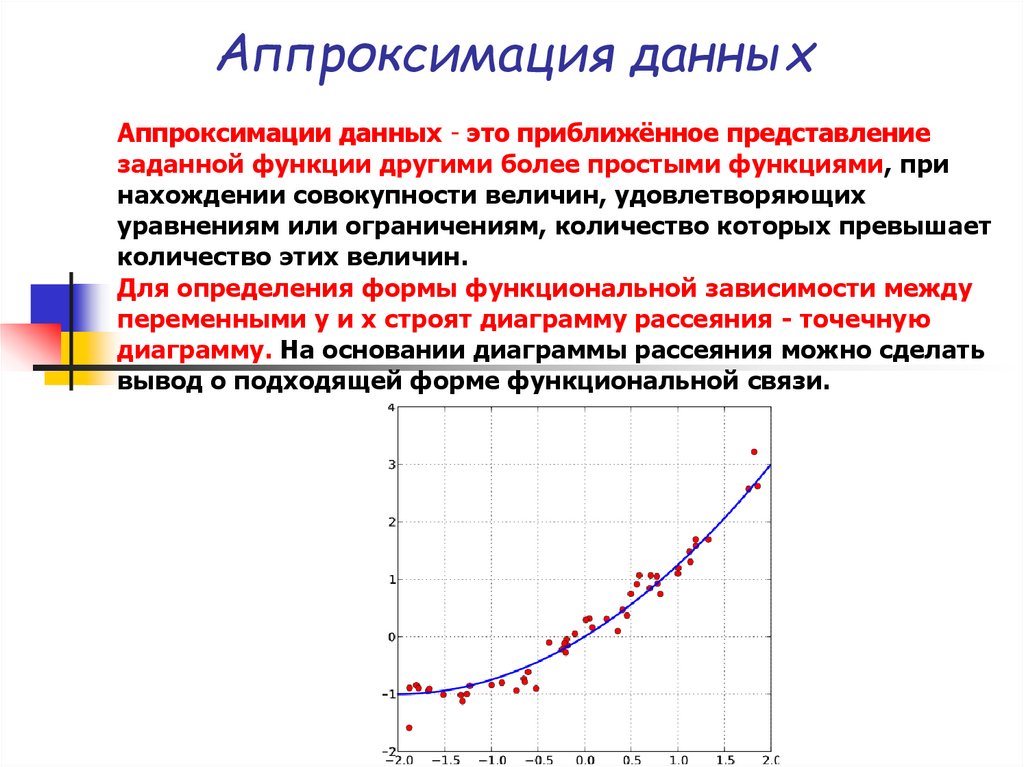
Аппроксимация данныхАппроксимации данных - это приближённое представление
заданной функции другими более простыми функциями, при
нахождении совокупности величин, удовлетворяющих
уравнениям или ограничениям, количество которых превышает
количество этих величин.
Для определения формы функциональной зависимости между
переменными y и х строят диаграмму рассеяния - точечную
диаграмму. На основании диаграммы рассеяния можно сделать
вывод о подходящей форме функциональной связи.
3.
Аппроксимация данныхЛинейная аппроксимация. Применяется для переменных,
которые увеличиваются или убывают с постоянной скоростью.
у=ах+b
где а – тангенс угла наклона, b – точка пересечения прямой
с осью у.
Логарифмическая аппроксимация. Применяется для
положительных и отрицательных величин, которые вначале
быстро растут или убывают, а затем постепенно стабилизируется.
у=сLnx+b
где с и b константы, Ln – натуральный логарифм.
Полиномиальная аппроксимация. Используется для описания
величин, попеременно возрастающих и убывающих. Применяют
для анализа большого набора данных нестабильной величины.
y=a+C1X1+C2X2+….+CjgXjg
где a, Cj-Cjg – константы. Максимальная величина степени
полинома – 18.
4.
Аппроксимация данныхСтепенная аппроксимация. Применяется, если зависимость,
которая содержится в данных, характеризуется постоянной
скоростью роста. Например, график ускорения автомобиля.
у=ахn
где а и n – константы.
Экспоненциальная аппроксимация. Используется в том
случае, если скорость изменения данных непрерывно возрастает.
у= а ebx
где а и b – константы.
Линейная фильтрация. Позволяет сгладить колебания данных
и таким образом более наглядно показать характер зависимости.
Такая линия строится по определенному числу точек.
Элементы данных усредняются, и полученный результат
используется в качестве среднего значения для
приближения. Для расчета скользящего среднего
используется уравнение
у= (Aj+Aj,i+….+Aj,n+i)/n.
5.
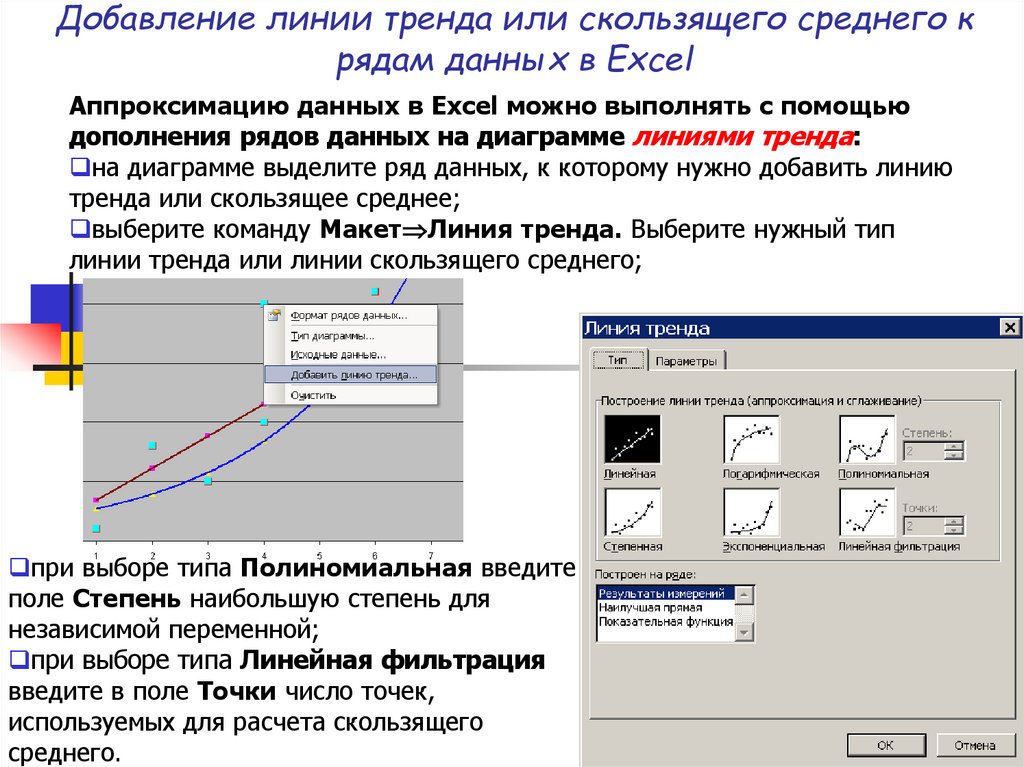
Добавление линии тренда или скользящего среднего крядам данных в Excel
Аппроксимацию данных в Excel можно выполнять с помощью
дополнения рядов данных на диаграмме линиями тренда:
на диаграмме выделите ряд данных, к которому нужно добавить линию
тренда или скользящее среднее;
выберите команду Макет Линия тренда. Выберите нужный тип
линии тренда или линии скользящего среднего;
при выборе типа Полиномиальная введите в
поле Степень наибольшую степень для
независимой переменной;
при выборе типа Линейная фильтрация
введите в поле Точки число точек,
используемых для расчета скользящего
среднего.
6.
Моделирование методом Монте-КарлоМетод Монте-Карло — численный метод, основанный на воспроизведении
большого числа реализаций случайного процесса, специально построенного
по условиям задачи.
1.Метод Монте – Карло позволяет моделировать любой процесс, на
протекание которого влияют случайные факторы.
2.Для многих математических задач, не связанных с какими – либо
случайностями, можно искусственно придумать вероятностную модель.
Метод применяется при исследовании
функционирования сложных систем, к
которым относятся разнообразные
производственные и информационные
системы, автоматизированные системы
управления, многопроцессорные,
вычислительные системы, некоторые
биологические, экономические системы.
Метод Монте-Карло в большей мере
используется для решения задач теории
массового обслуживания, задач теории игр
и математической экономики, задач теории
передачи сообщений при наличии помех и
ряд других.




 Математика
Математика








