Механизмы и способы генерации и усиления ультракоротких (пикосекундных и фемтосекундных) лазерных импульсов

1.

КУРС ЛЕКЦИЙ, МИФИ, 2025г.
ИОФ РАН
Механизмы
и способы генерации иИМПУЛЬСОВ
усиления ультракоротких
" ЛАЗЕРЫ
УЛЬТРАКОРОТКИХ
" Каф. 69
(пикосекундных и фемтосекундных) лазерных импульсов; методы
" измерения
ФИЗИКА их
УЛЬТРАКОРОТКИХ
" Каф. 98
основных параметров;ИМПУЛЬСОВ
практические применения.
Гарнов Сергей Владимирович
Институт общей физики им. А.М. Прохорова РАН
Лекция №7. 1 апреля 2025г.
1. Управление пространственно-временным спектром УКИ – дифракционные
решетки. 2. Как ультракороткие импульсы преобразуются дифракционными
решетками? 3. Схемы компенсации чирпа.

2.

ИОФ РАН
Управление
пространственно-временной
структурой и спектром УКИ:
дифракционные решетки

3.

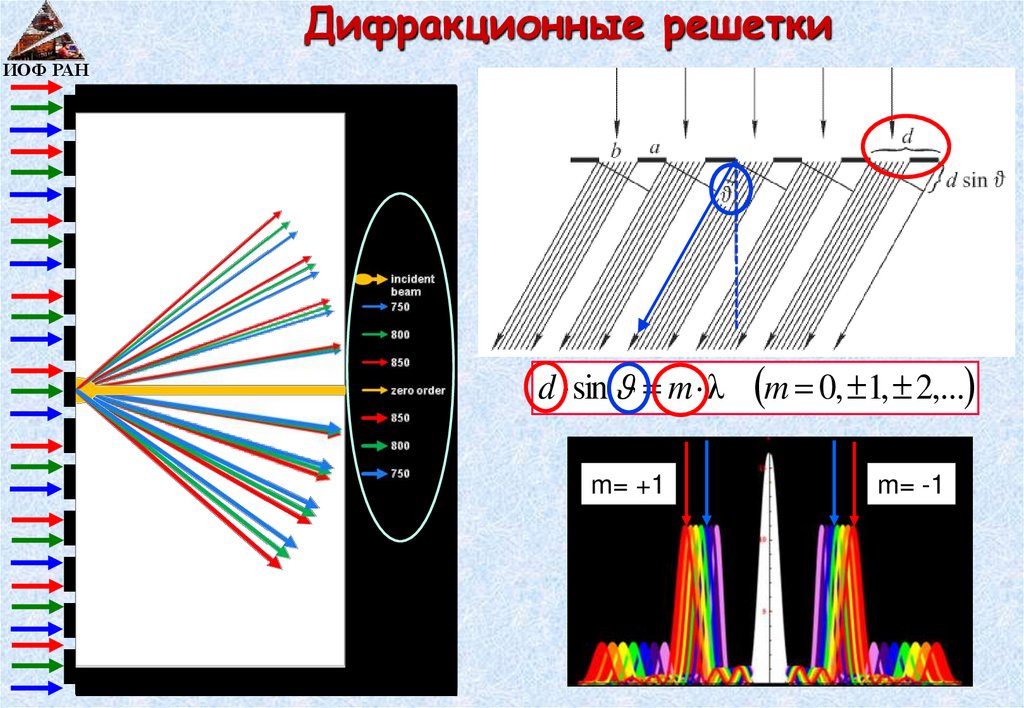
Дифракционные решетки
ИОФ РАН
d sin m λ
m= +1
m 0, 1, 2,...
m= -1

4.

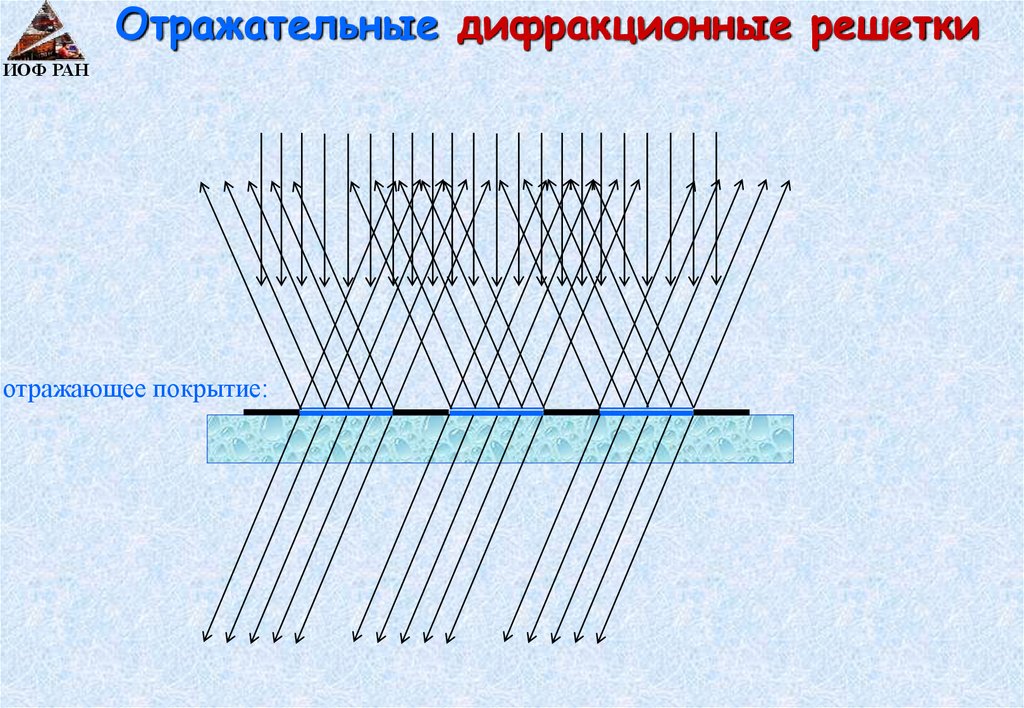
Отражательные дифракционные решетки
ИОФ РАН
отражающее покрытие:

5.

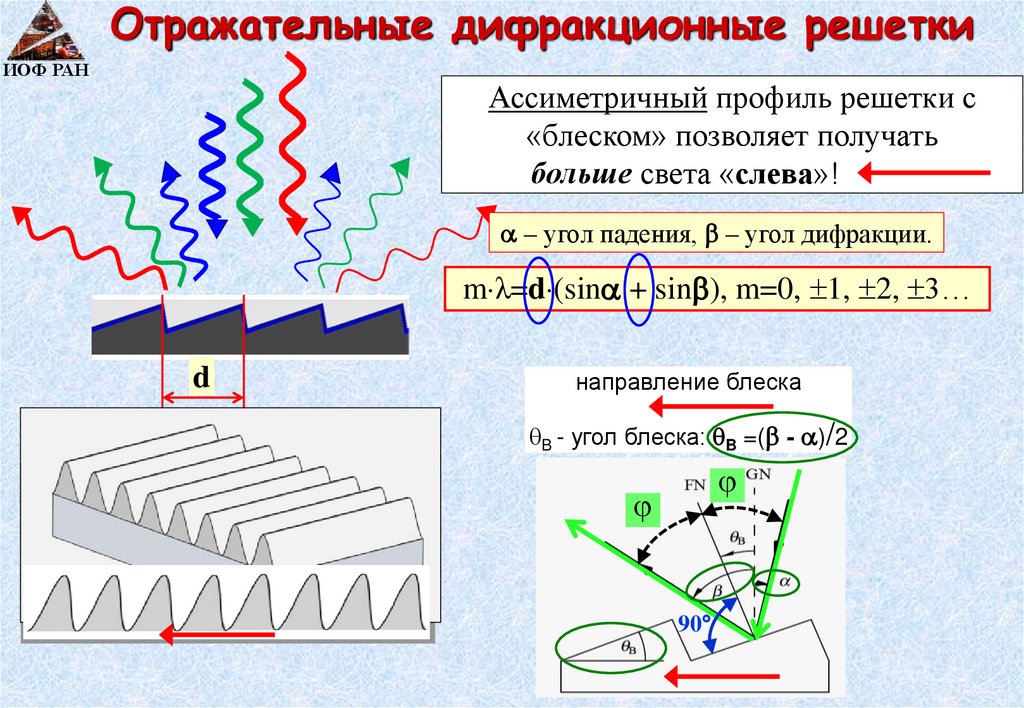
Отражательные дифракционные решетки
ИОФ РАН
Ассиметричный профиль решетки с
«блеском» позволяет получать
больше света «слева»!
– угол падения, – угол дифракции.
m λ=d (sin + sin ), m=0, 1, 2, 3…
d
направление блеска
метал (золото)
эпоксид
подложка
B - угол блеска: B =( - )/2
90

6.

Дифракционные решетки
ИОФ РАН
Diffraction Grating.xlsx
http://terpconnect.umd.edu/~toh/models/DiffractionGrating.html,
См. файл «Diffraction Grating.xlsx» - в папке лекции № 7.

7.

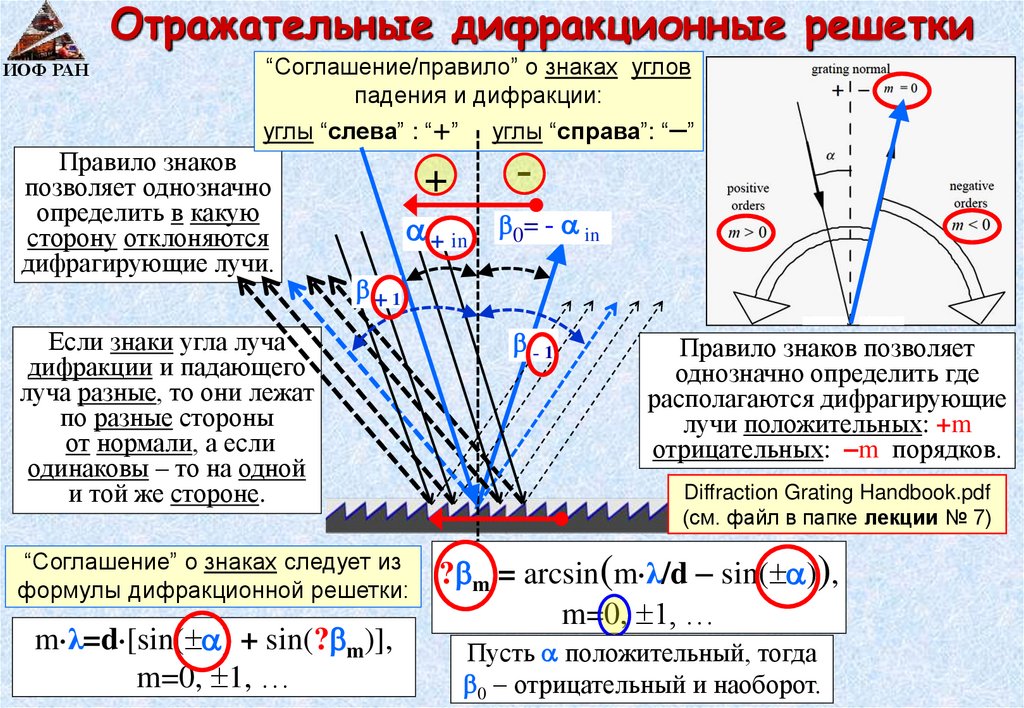
Отражательные дифракционные решетки
ИОФ РАН
“Соглашение/правило” о знаках углов
падения и дифракции:
углы “слева” : “+”
Правило знаков
позволяет однозначно
определить в какую
сторону отклоняются
дифрагирующие лучи.
+
углы “справа”: “ ”
-
in 0= - in
1
Если знаки угла луча
дифракции и падающего
луча разные, то они лежат
по разные стороны
от нормали, а если
одинаковы – то на одной
и той же стороне.
“Соглашение” о знаках следует из
формулы дифракционной решетки:
m λ=d [sin( ) + sin(? m)],
m=0, 1, …
-1
Правило знаков позволяет
однозначно определить где
располагаются дифрагирующие
лучи положительных: +m
отрицательных: –m порядков.
Diffraction Grating Handbook.pdf
(см. файл в папке лекции № 7)
? m = arcsin(m λ/d sin( )),
m=0, 1, …
Пусть положительный, тогда
0 отрицательный и наоборот.

8.

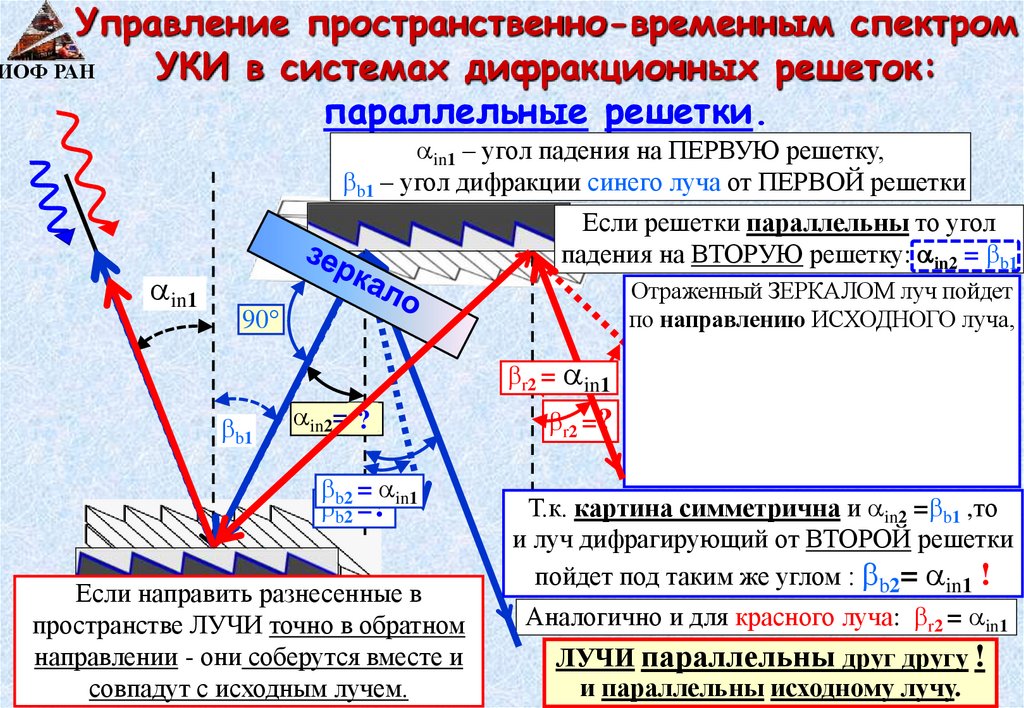
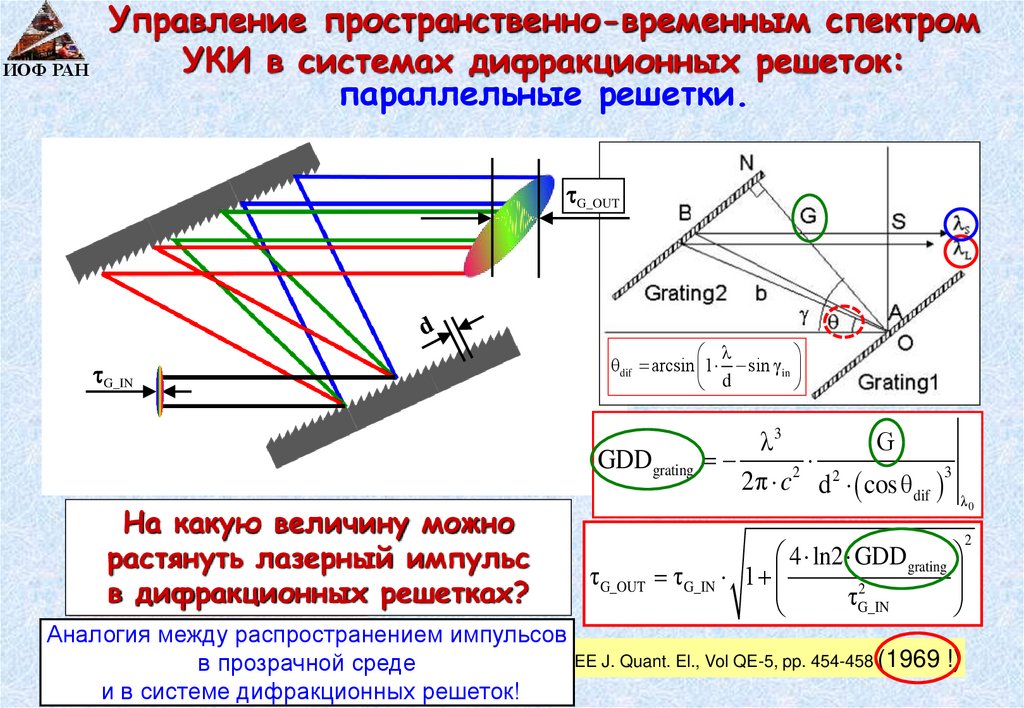
Управление пространственно-временным спектром
ИОФ РАН
УКИ в системах дифракционных решеток:
параллельные решетки.
in1 – угол падения на ПЕРВУЮ решетку,
b1 – угол дифракции синего луча от ПЕРВОЙ решетки
in1
Если решетки параллельны то угол
падения на ВТОРУЮ решетку: in2 = b1
90
b1
in2= ?b1
b2 = in1
b2 =?
Если направить разнесенные в
пространстве ЛУЧИ точно в обратном
направлении - они соберутся вместе и
совпадут с исходным лучем.
Отраженный ЗЕРКАЛОМ луч пойдет
по направлению ИСХОДНОГО луча,
а поскольку формула решетки
r2 = in1 СИММЕТРИЧНА по углам и :
m λ = d (sin + sin )
r2 =? он «отразится» от ПЕРВОЙ решетки
под углом in1 !
Т.к. картина симметрична и in2 = b1 ,то
и луч дифрагирующий от ВТОРОЙ решетки
пойдет под таким же углом : b2= in1 !
Аналогично и для красного луча: r2 = in1
ЛУЧИ параллельны друг другу !
и параллельны исходному лучу.

9.

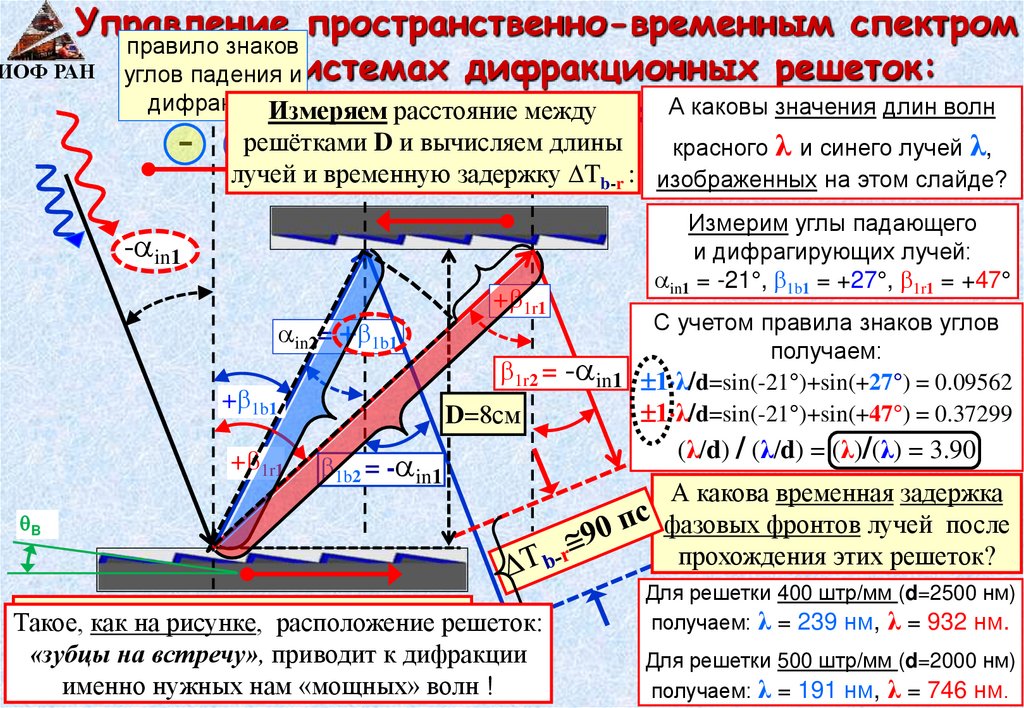
Управление пространственно-временным спектром
правило знаков
ИОФ РАН углов
УКИ
в системах
дифракционных решеток:
падения
и
дифракции:Измеряем расстояние между
А каковы значения длин волн
параллельные решетки.
D и вычисляем длины
- лучей
+решётками
и временную задержку T :
b-r
- in1
in2= + 1b1
+ 1b1
+ 1r1
+ 1r1
красного λ и синего лучей λ,
изображенных на этом слайде?
Измерим углы падающего
и дифрагирующих лучей:
in1 = -21 , 1b1 = +27 , 1r1 = +47
С учетом правила знаков углов
получаем:
1r2 = - in1 1 λ/d=sin(-21 )+sin(+27 ) = 0.09562
1 λ/d=sin(-21 )+sin(+47 ) = 0.37299
D=8см
1b2 = - in1
B
В параллельных
решетках
возникаетрешеток:
Такое,
как на рисунке,
расположение
чирп! к дифракции
«зубцыотрицательный
на встречу», приводит
именно нужных нам «мощных» волн !
(λ/d) / (λ/d) = (λ)/(λ) = 3.90
А какова временная задержка
фазовых фронтов лучей после
прохождения этих решеток?
Для решетки 400 штр/мм (d=2500 нм)
получаем: λ = 239 нм, λ = 932 нм.
Для решетки 500 штр/мм (d=2000 нм)
получаем: λ = 191 нм, λ = 746 нм.

10.

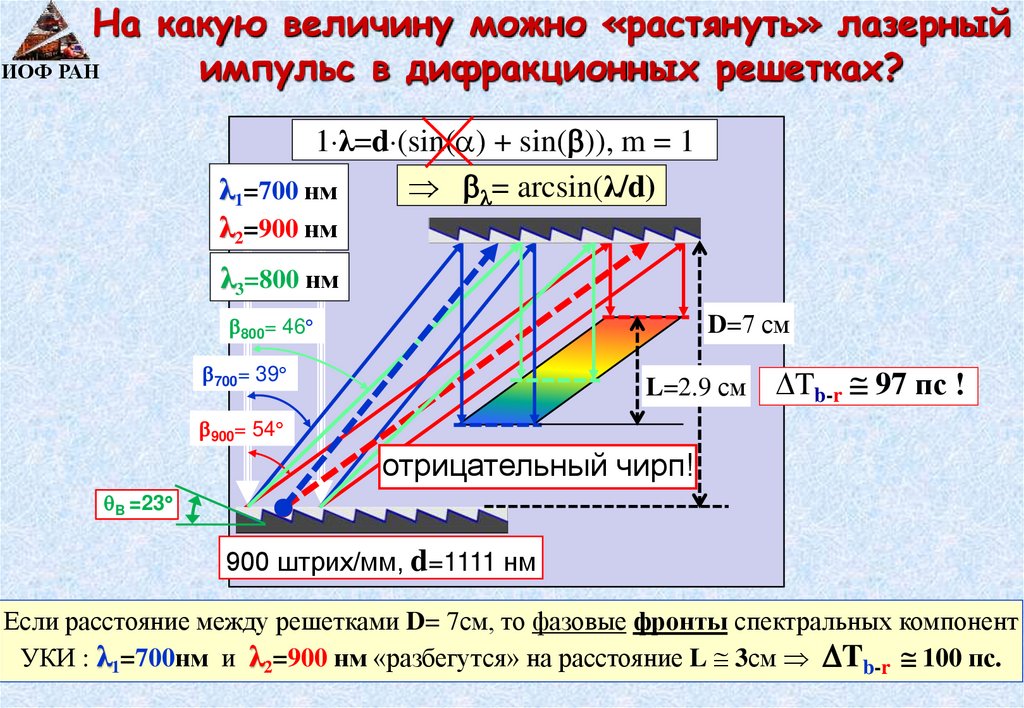
На какую величину можно «растянуть» лазерный
ИОФ РАН
импульс в дифракционных решетках?
1 λ=d (sin( ) + sin( )), m = 1
= arcsin(λ/d)
λ1=700 нм
λ2=900 нм
λ3=800 нм
D=7 см
800= 46
700= 39
L=2.9 см
Tb-r 97 пс !
900= 54
отрицательный чирп!
B =23
900 штрих/мм, d=1111 нм
Если расстояние между решетками D= 7см, то фазовые фронты спектральных компонент
УКИ : λ1=700нм и λ2=900 нм «разбегутся» на расстояние L 3см Tb-r 100 пс.

11.

На какую величину можно «растянуть» лазерный
ИОФ РАН
импульс в дифракционных решетках?
λ1=700 нм
λ2=900 нм
λ3=800 нм
отрицательный чирп!
2L=5.8 см
Так устроен
т.н.«СТРЕТЧЕР»
(«растяжитель»
импульса)
D=7 см
2 Tb-r 194 пс
Tb-r 97 пс !
L=2.9 см
зеркало Красный луч задержался на 2L
900 штрих/мм, d=1111 нм
В результате, фазовые фронты спектральных компонент УКИ λ1=700нм и λ2=900 нм
«разбежались» на удвоенное расстояние: 2L 5.8 см.
А поля спектральных компонент пространственно выпрямились!

12.

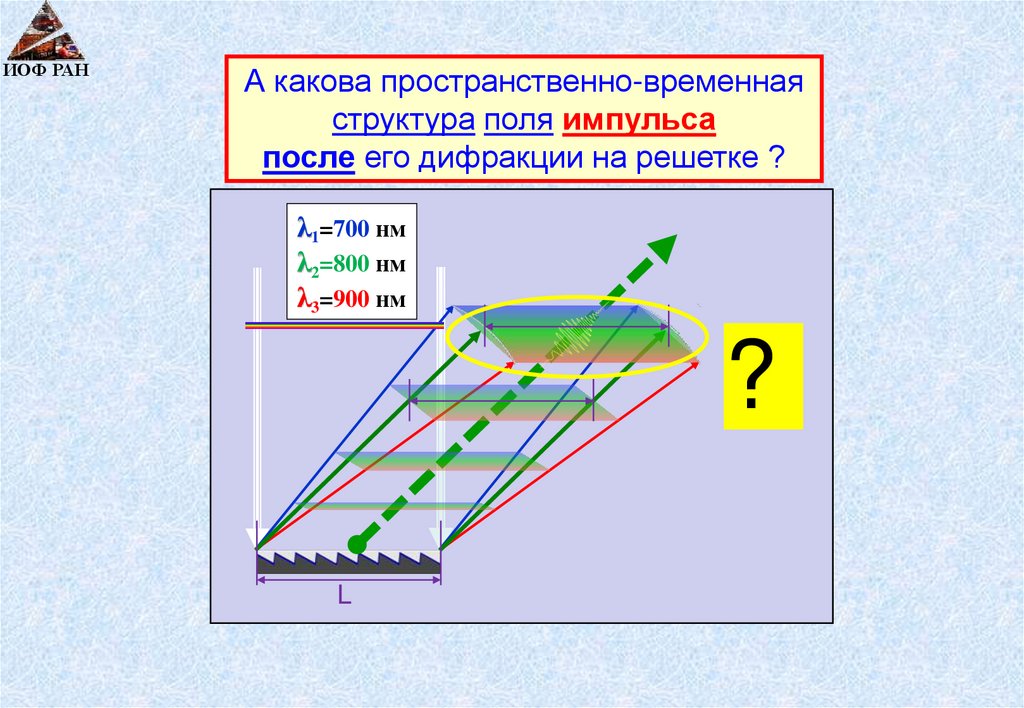
ИОФ РАН
А какова пространственно-временная
структура поля импульса
после его дифракции на решетке ?
λ1=700 нм
λ2=800 нм
λ3=900 нм
?
L

13.

ИОФ РАН
Управление пространственно-временной
структурой и спектром УКИ.
дифракционные решетки
А как
ультра короткие импульсы
ПРЕОБРАЗУЮТСЯ
дифракционными решетками ???

14.

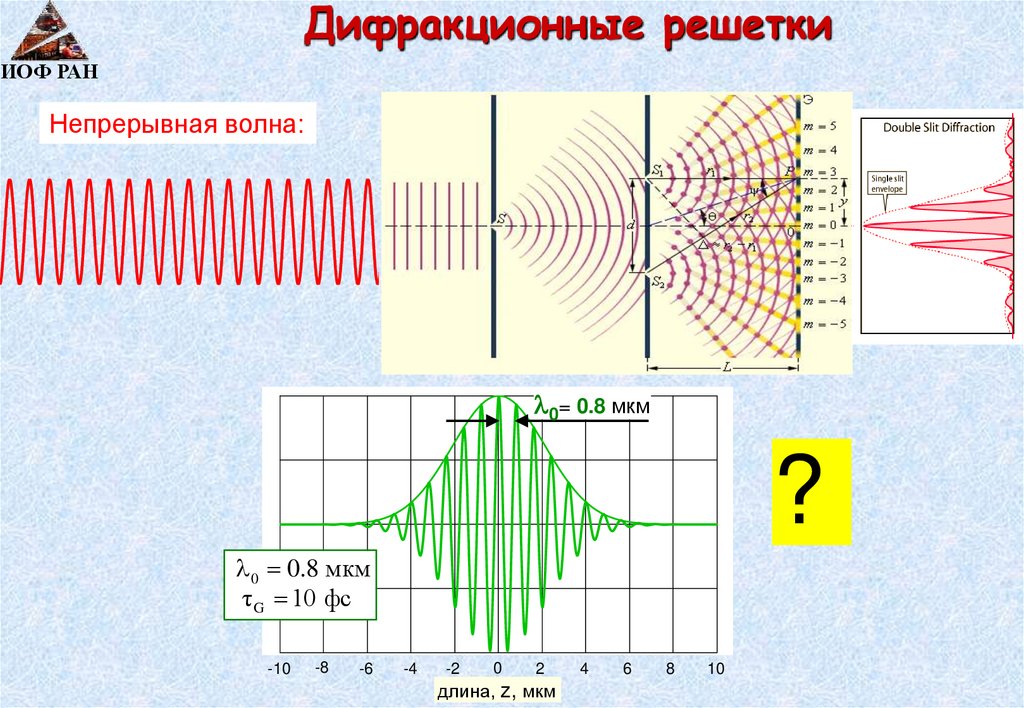
Дифракционные решетки
ИОФ РАН
Непрерывная волна:
F10_C2
0
100
x0 = -100
2002002002002
0= 0.8 мкм
?
0 0.8 мкм
τ G 10 фс
10
-10
8
-8
6
-6
4
-4
2
-2
0
0
2
2
длина, z, мкм
4
4
6
6
8
8
10
10

15.

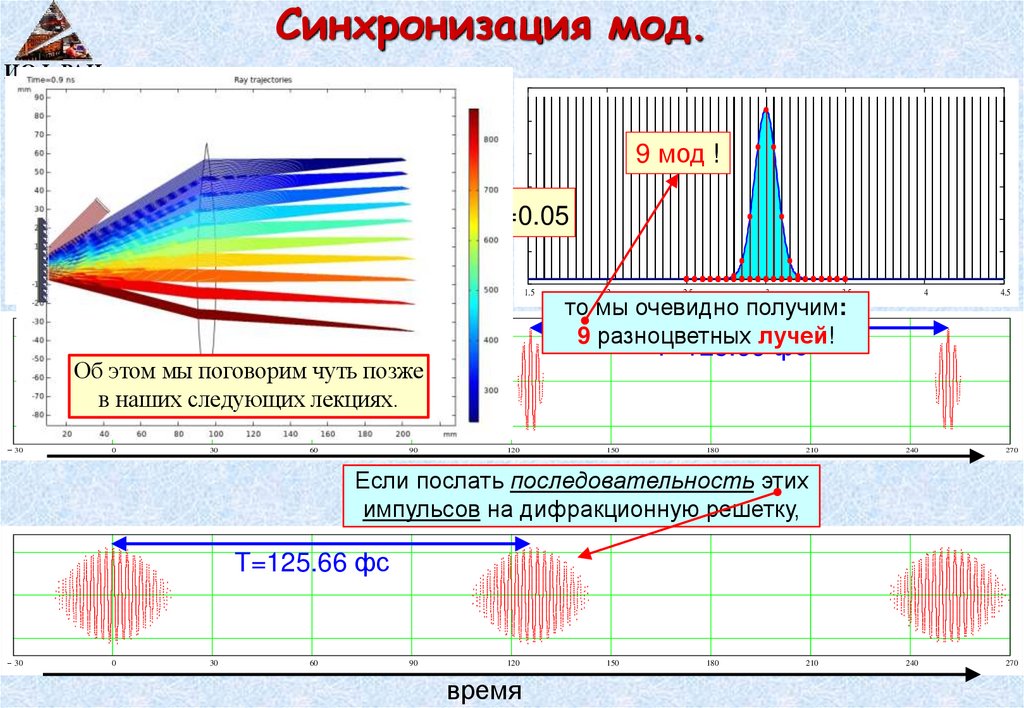
Синхронизация мод.
ИОФ РАН
9 мод !
50 мод !
=0.05
1.5
2
2.5
3
3.5
4
4.5
1.5
E ,R (x, t) A ωm cos ωm c x c t
2
30
60
90
3.5
4
4.5
T=125.66 фс
Об этом мы поговорим чуть позже
в наших следующих лекциях.
0
3
то мы очевидно получим:
9 разноцветных лучей!
m
30
2.5
120
150
180
210
240
270
240
270
время
Если послать
последовательность этих
импульсов на дифракционную решетку,
T=125.66 фс
30
0
30
60
90
120
время
150
180
210

16.

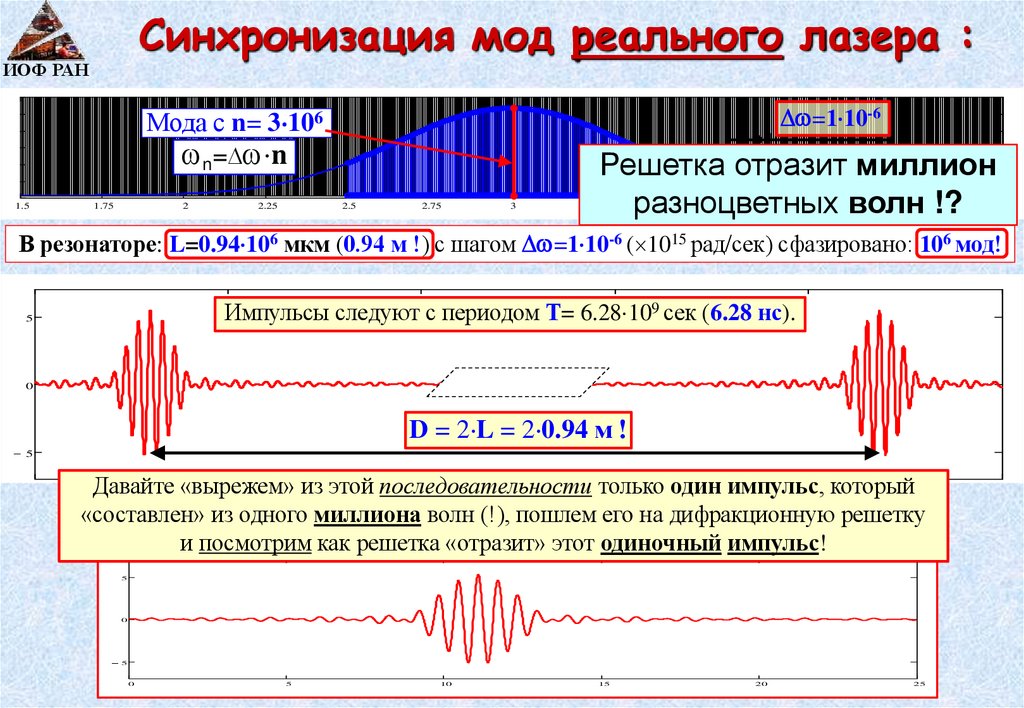
Синхронизация мод реального лазера :
ИОФ РАН
=1 10-6
Мода с n= 3 106
n= n
1.5
1.75
2
2.25
2.5
2.75
3
Решетка отразит миллион
разноцветных волн !?
3.25
3.5
3.75
4
4.25
4.5
В резонаторе: L=0.94 106 мкм (0.94 м !) с шагом =1 10-6 ( 1015 рад/сек) сфазировано: 106 мод!
Импульсы следуют с периодом Т= 6.28 109 сек (6.28 нс).
5
0
D = 2 L = 2 0.94 м !
5
0
Давайте «вырежем» из этой последовательности только один импульс, который
«составлен» из одного миллиона волн (!), пошлем его на дифракционную решетку
и посмотрим как решетка «отразит» этот одиночный импульс!
10
20
30
40
5
0
5
0
5
10
15
20
25
50

17.

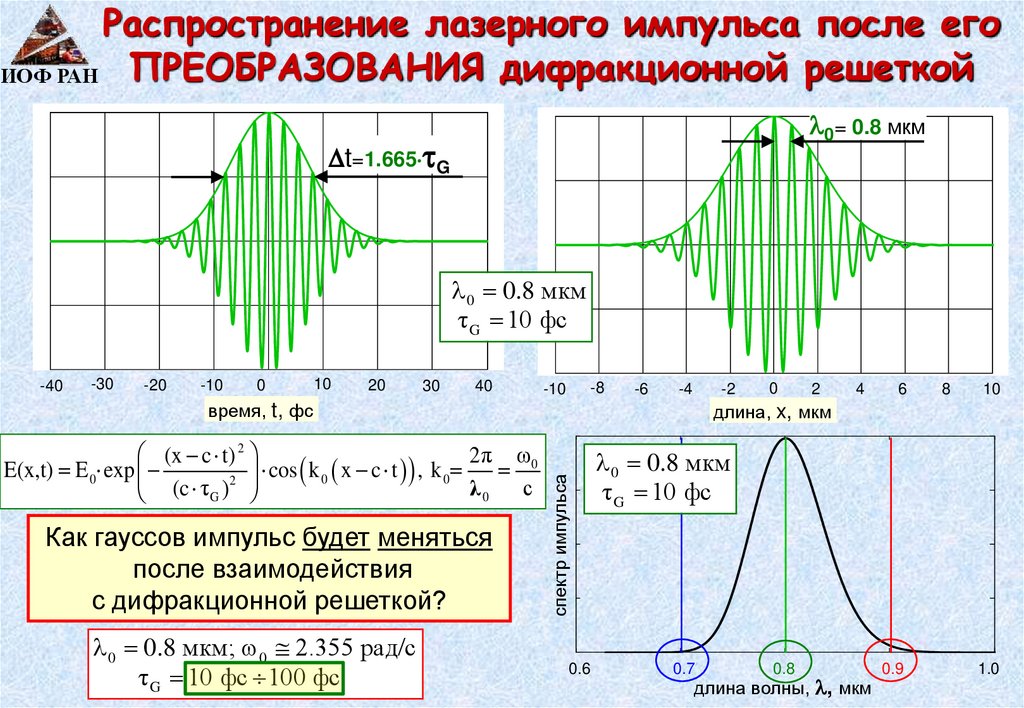
Распространение лазерного импульса после его
ИОФ РАН ПРЕОБРАЗОВАНИЯ дифракционной решеткой
0= 0.8 мкм
t=1.665 G
0 0.8 мкм
τ G 10 фс
40
-40
30
-30
20
-20
10
-10
0
0
10
10
20
20
30
30
40
40
10
8
-8
-10
6
-6
4
-4
время, t, фс
Как гауссов импульс будет меняться
после взаимодействия
с дифракционной решеткой?
0 0.8 мкм; 0 2.355 рад/с
τ G 10 фс 100 фс
0
2
0
2
4
6
4
6
8
8
10
10
длина, x, мкм
0 0.8 мкм
τ G 10 фс
спектр импульса
(x c t) 2
2π ω0
E(x,t) E 0 exp
cos
k
x
c
t
,
k
0
0
2
λ0 c
(c τ G )
2
-2
0.6
0.6
0.7
0.7
0.8
0.8
длина волны, , мкм
0.9
0.9
1
1.0

18.

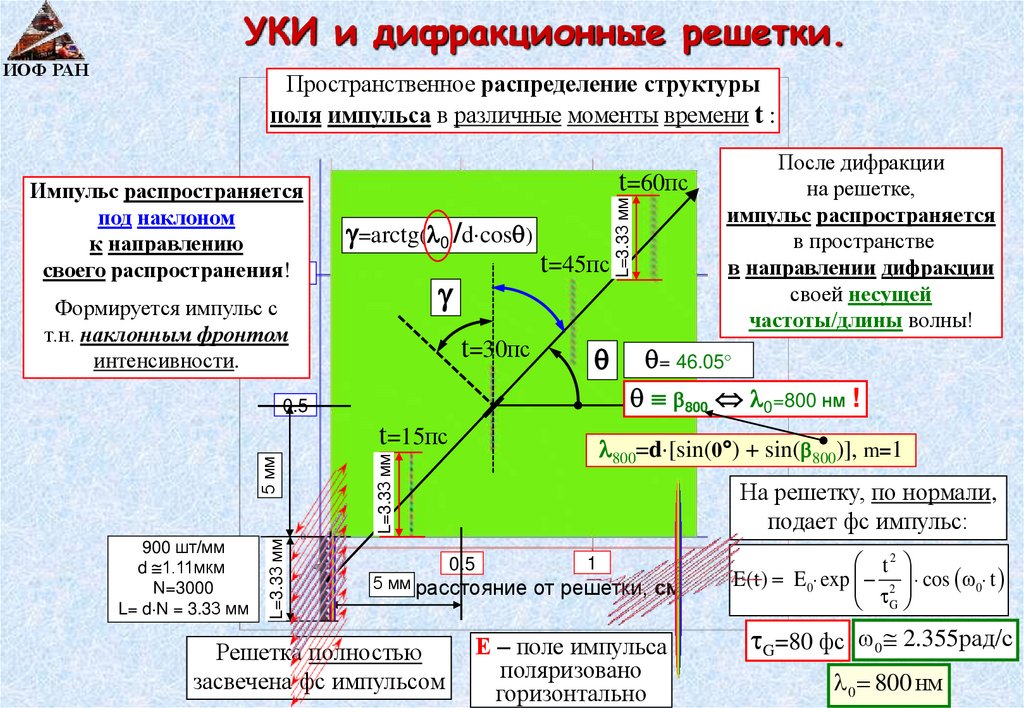
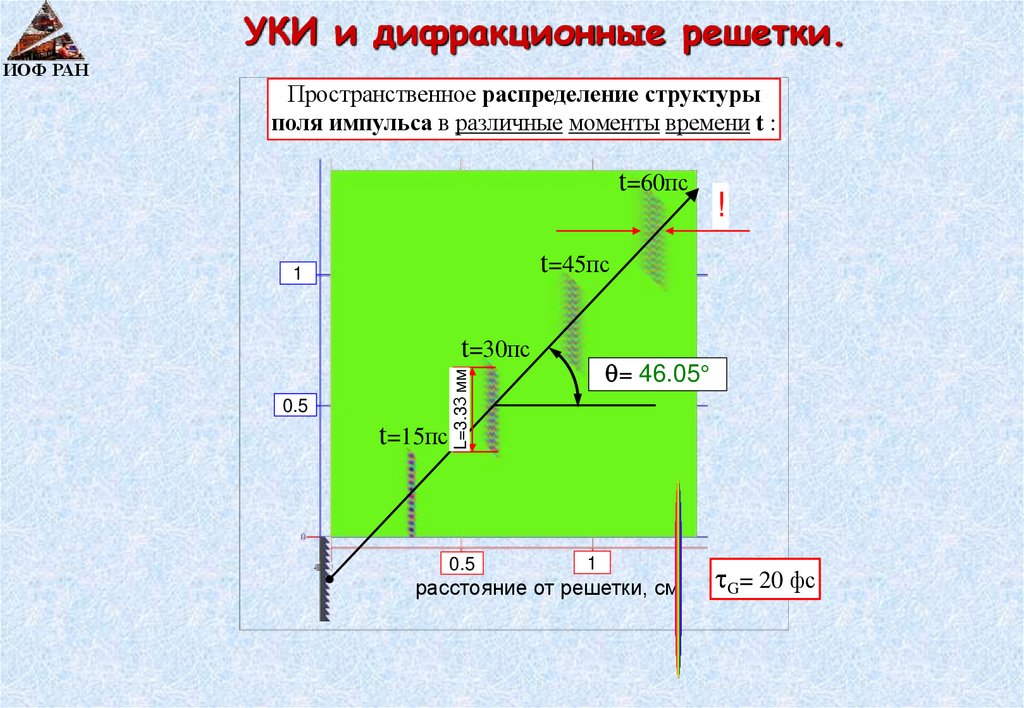
УКИ и дифракционные решетки.
ИОФ РАН
Пространственное распределение структуры
поля импульса в различные моменты времени t :
t=60пс
=arctg( 0 /d cos )
t=45пс
Формируется импульс с
т.н. наклонным фронтом
интенсивности.
t=30пс
0.5
900 шт/мм
d 1.11мкм
N=3000
L= d N = 3.33 мм
L=3.33 мм
= 46.05
800 0=800 нм !
800=d [sin(0 ) + sin( 800)], m=1
L=3.33 мм
5 мм
t=15пс
L=3.33 мм
Импульс распространяется
под наклоном
к направлению
своего распространения! 1
На решетку, по нормали,
подает фс импульс:
0.5
1
5 мм расстояние от решетки, см
Решетка полностью
засвечена фс импульсом
После дифракции
на решетке,
импульс распространяется
в пространстве
в направлении дифракции
своей несущей
частоты/длины волны!
Е – поле импульса
поляризовано
горизонтально
t2
E(t) E 0 exp 2 cos 0 t
G
G=80 фс 0 2.355рад/с
0 800 нм

19.

УКИ и дифракционные решетки.
ИОФ РАН
Представленные здесь и ниже расчетные
распределения пространственной структуры поля
ультракороткого лазерного импульса
получены с использованием простейшей модели
взаимодействия УКИ с дифракционными решётками.
О ней мы поговорим в следующей лекции,
а сейчас продолжим.

20.

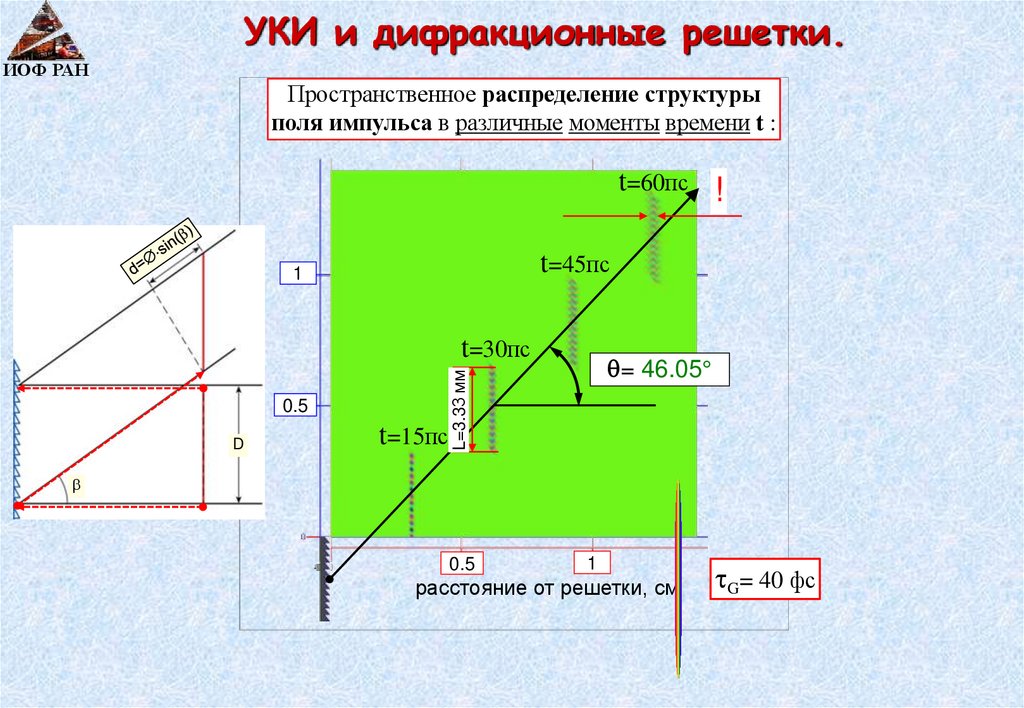
УКИ и дифракционные решетки.
ИОФ РАН
Пространственное распределение структуры
поля импульса в различные моменты времени t :
t=60пс !
t=45пс
1
t=30пс
D
t=15пс
L=3.33 мм
0.5
= 46.05
0.5
1
расстояние от решетки, см
G= 40 фс

21.

УКИ и дифракционные решетки.
ИОФ РАН
Пространственное распределение структуры
поля импульса в различные моменты времени t :
t=60пс
!
t=45пс
1
t=30пс
t=15пс
L=3.33 мм
0.5
= 46.05
0.5
1
расстояние от решетки, см
G= 20 фс

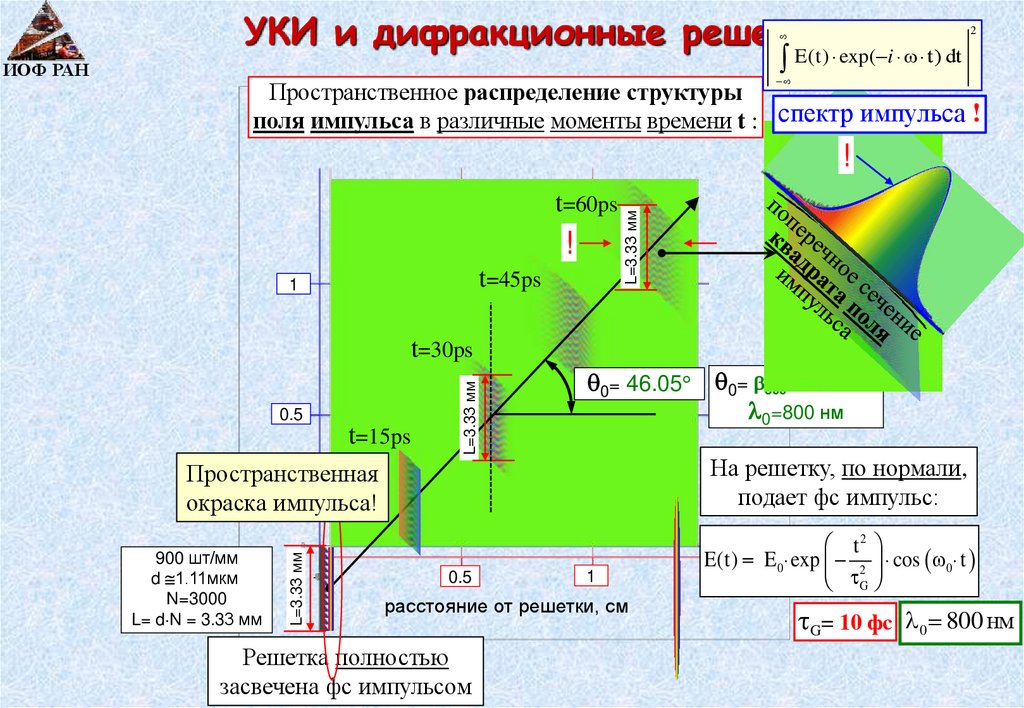
22.

УКИ и дифракционные решетки.
E(t) exp( i ω t) dt
Пространственное распределение структуры
поля импульса в различные моменты времени t : спектр импульса !
t=60ps
!
t=45ps
1
L=3.33 мм
!
0.5
t=15ps
L=3.33 мм
t=30ps
0= 46.05
900 шт/мм
d 1.11мкм
N=3000
L= d N = 3.33 мм
0.5
1
расстояние от решетки, см
Решетка полностью
засвечена фс импульсом
0= 800= – 46.05
0=800 нм
На решетку, по нормали,
подает фс импульс:
Пространственная
окраска импульса!
L=3.33 мм
ИОФ РАН
2
t2
E(t) E 0 exp 2 cos 0 t
G
G= 10 фс 0 800 нм

23.

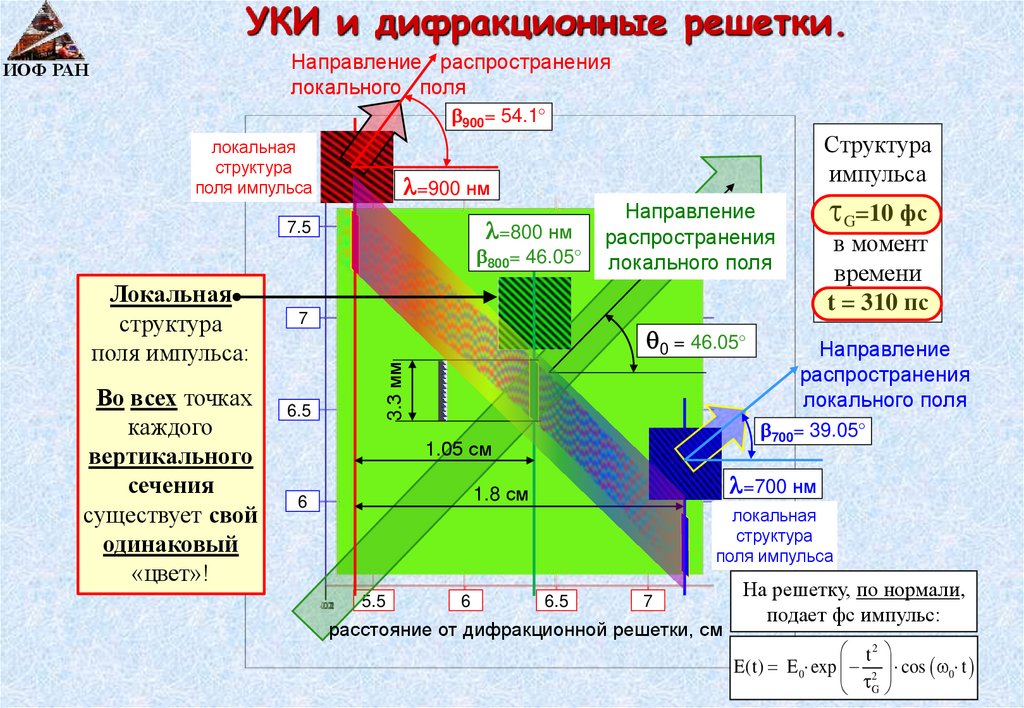
УКИ и дифракционные решетки.
Направление распространения
локального поля
ИОФ РАН
900= 54.1
локальная
структура
поля импульса
Структура
импульса
=900 нм
=800 нм
7.5
800= 46.05
Во всех точках
каждого
вертикального
сечения
существует свой
одинаковый
«цвет»!
7
6.5
0 = 46.05
3.3 мм
Локальная
структура
поля импульса:
в момент
времени
t = 310 пс
Направление
распространения
локального поля
700= 39.05
1.05 см
=700 нм
1.8 см
6
G=10 фс
Направление
распространения
локального поля
локальная
структура
поля импульса
5.5
6
6.5
7
расстояние от дифракционной решетки, см
На решетку, по нормали,
подает фс импульс:
t2
E(t) E 0 exp 2 cos 0 t
G

24.

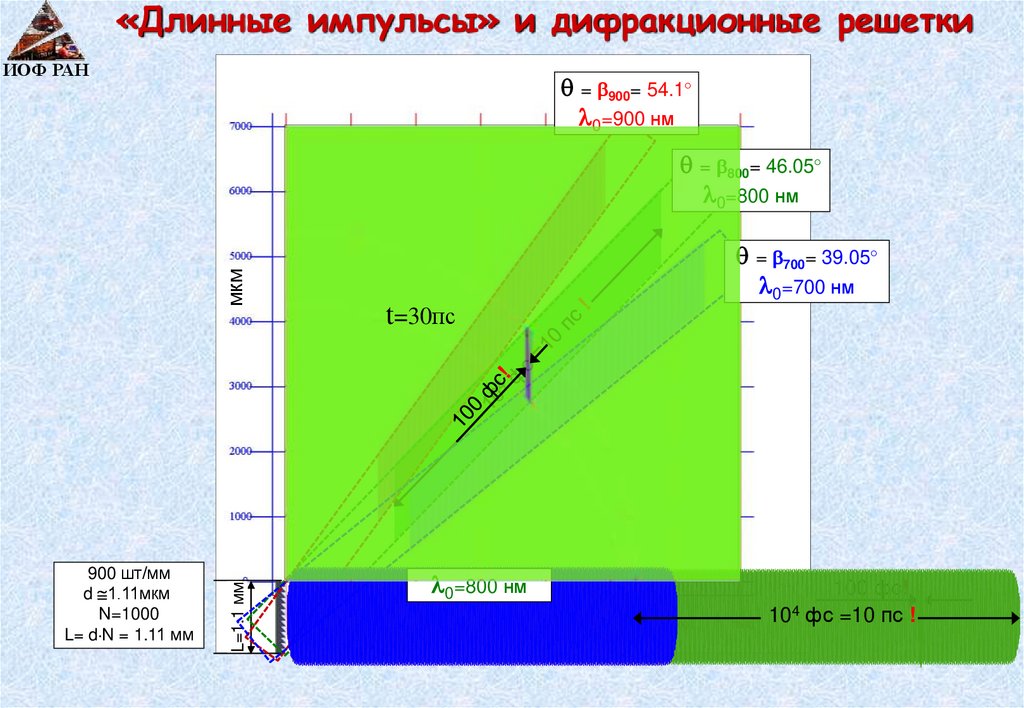
«Длинные импульсы» и дифракционные решетки
ИОФ РАН
= 900= 54.1
0=900 нм
900 шт/мм
d 1.11мкм
N=1000
L= d N = 1.11 мм
L=1.1 мм
мкм
= 800= 46.05
0=800 нм
= 700= 39.05
0=700 нм
t=30пс
0=800 нм
100 фс!
104 фс =10 пс !

25.

Управление пространственно-временным спектром
УКИ в системах дифракционных решеток:
ИОФ РАН
параллельные решетки.
G_OUT
G_IN
На какую величину
можно
2
2лазерный
GVD x
растянуть
импульс
τout x τG 1
GVD
x GDD
2
в дифракционных
τG
решетках?
λ
θ dif arcsin 1 sin γ in
d
λ3
G
GDDgrating
2
2
2π c d cosθdif 3
λ0
4 ln2 GDDgrating
τ G_OUT τ G_IN 1
2
τ G_IN
Аналогия между распространением импульсов
E.B. Treacy, Optical
Compression
With Diffraction Gratings, IEEE J. Quant. El., Vol QE-5, pp. 454-458 (1969 !)
в Pulse
прозрачной
среде
и в системе дифракционных решеток!
2

26.

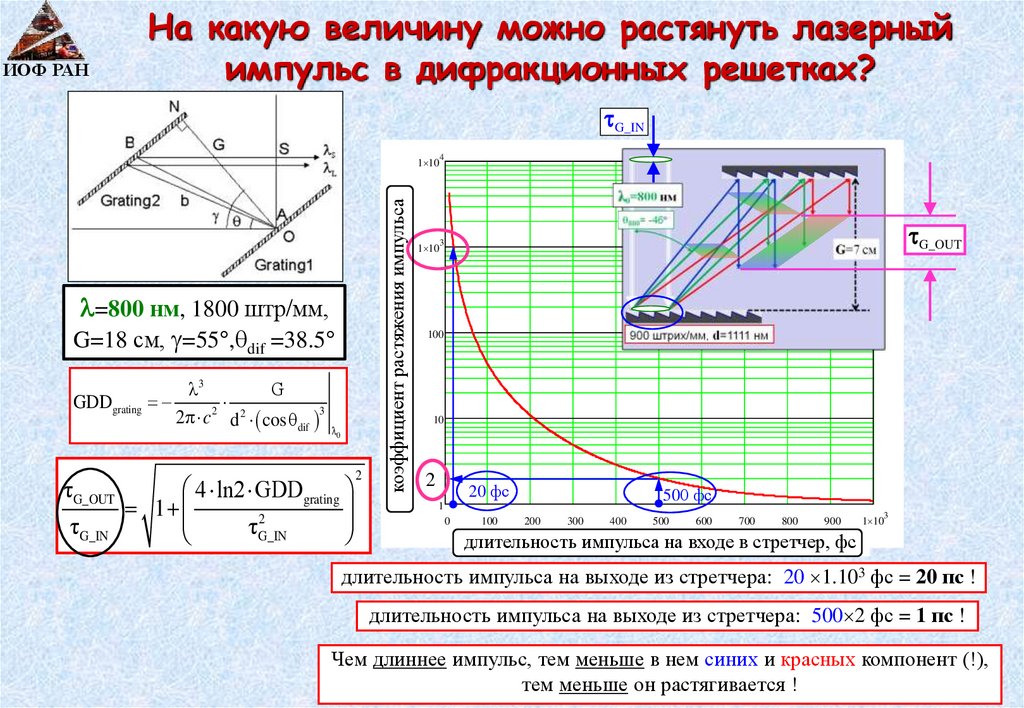
ИОФ РАН
На какую величину можно растянуть лазерный
импульс в дифракционных решетках?
=800 нм, 1800 штр/мм,
G=18 см, =55 , dif =38.5
λ3
G
GDDgrating
2
2
2π c d cosθdif 3
λ0
4 ln2 GDDgrating
1
2
τ G_IN
τ
G_IN
τ G_OUT
2
коэффициент растяжения импульса
G_IN
1 10
4
1 10
3
G_OUT
100
10
2
20 фс
500 фс
1
0
100
200
300
400
500
600
700
800
900
1 10
3
длительность импульса на входе в стретчер, фс
длительность импульса на выходе из стретчера: 20 1.103 фс = 20 пс !
длительность импульса на выходе из стретчера: 500 2 фс = 1 пс !
Чем длиннее импульс, тем меньше в нем синих и красных компонент (!),
тем меньше он растягивается !

27.

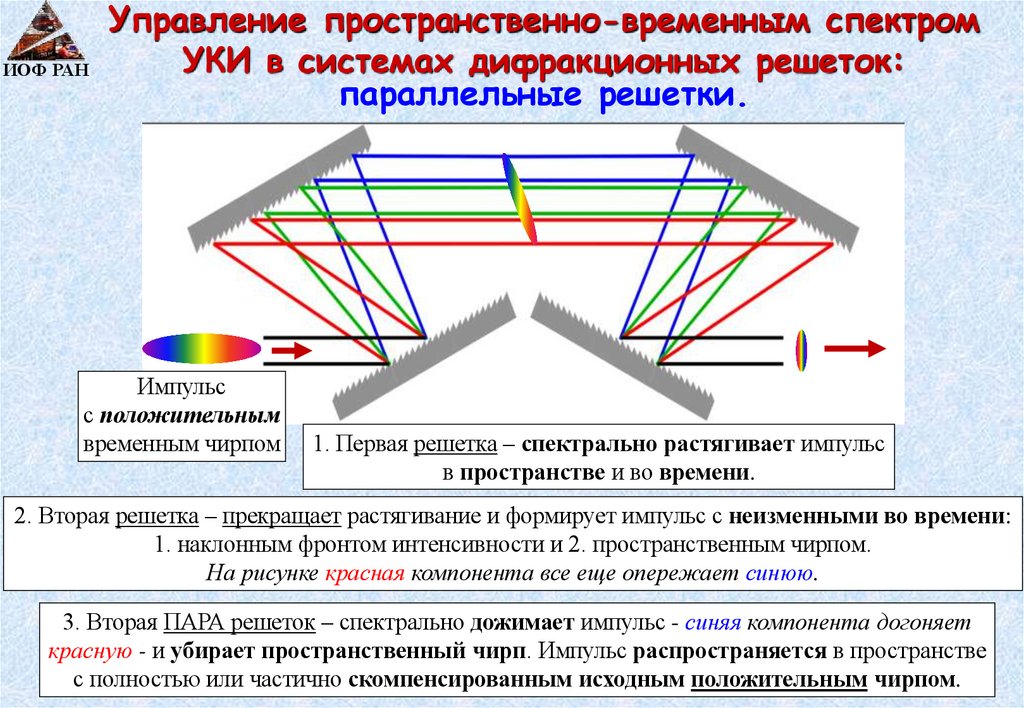
Управление пространственно-временным спектром
УКИ в системах дифракционных решеток:
ИОФ РАН
параллельные решетки.
Импульс
с положительным
временным чирпом
1. Первая решетка – спектрально растягивает импульс
в пространстве и во времени.
2. Вторая решетка – прекращает растягивание и формирует импульс с неизменными во времени:
1. наклонным фронтом интенсивности и 2. пространственным чирпом.
На рисунке красная компонента все еще опережает синюю.
3. Вторая ПАРА решеток – спектрально дожимает импульс - синяя компонента догоняет
красную - и убирает пространственный чирп. Импульс распространяется в пространстве
с полностью или частично скомпенсированным исходным положительным чирпом.

28.

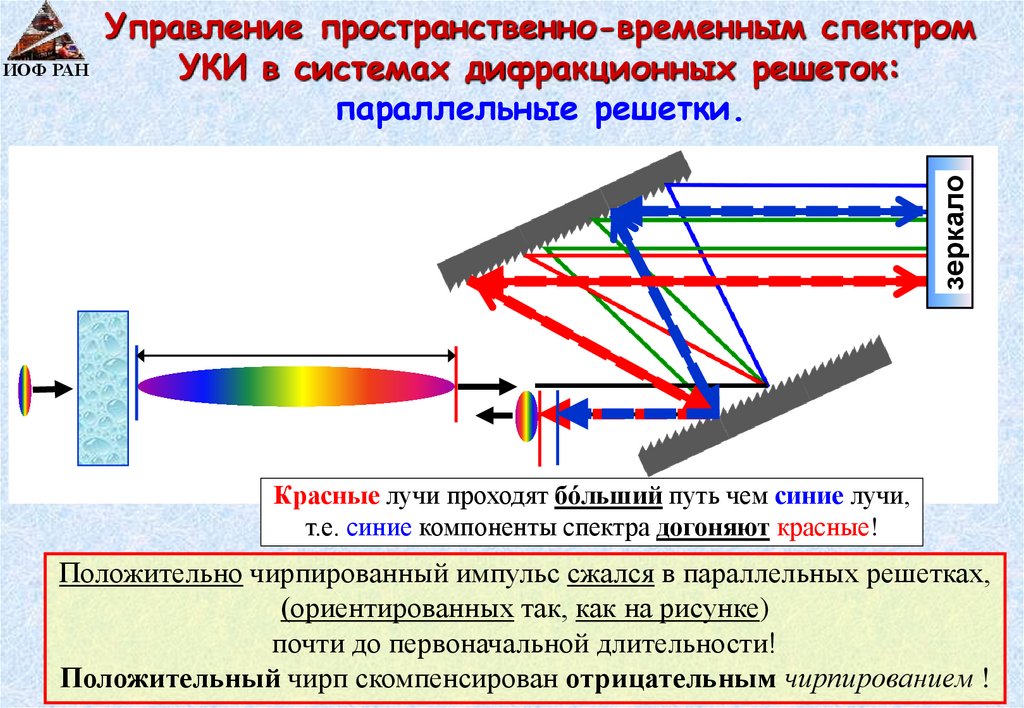
зеркало
Управление пространственно-временным спектром
ИОФ РАН
УКИ в системах дифракционных решеток:
параллельные решетки.
Красные лучи проходят бóльший путь чем синие лучи,
т.е. синие компоненты спектра догоняют красные!
Положительно чирпированный импульс сжался в параллельных решетках,
(ориентированных так, как на рисунке)
почти до первоначальной длительности!
Положительный чирп скомпенсирован отрицательным чирпированием !

29.

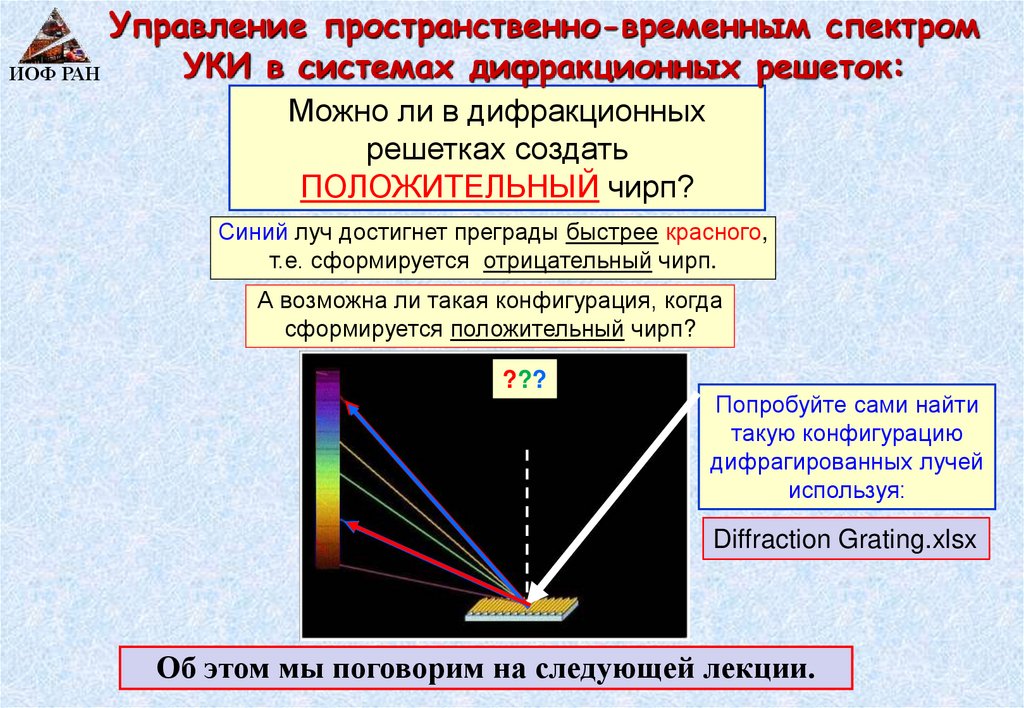
Управление пространственно-временным спектром
УКИ в системах дифракционных решеток:
ИОФ РАН
Можно ли в дифракционных
решетках создать
ПОЛОЖИТЕЛЬНЫЙ чирп?
Синий луч достигнет преграды быстрее красного,
т.е. сформируется отрицательный чирп.
А возможна ли такая конфигурация, когда
сформируется положительный чирп?
???
Попробуйте сами найти
такую конфигурацию
дифрагированных лучей
используя:
Diffraction Grating.xlsx
Об этом мы поговорим на следующей лекции.