Оптика. Метод зон Френеля (лекция 3)

1.

МЕТОД
ЗОН
ФРЕНЕЛЯ

2.

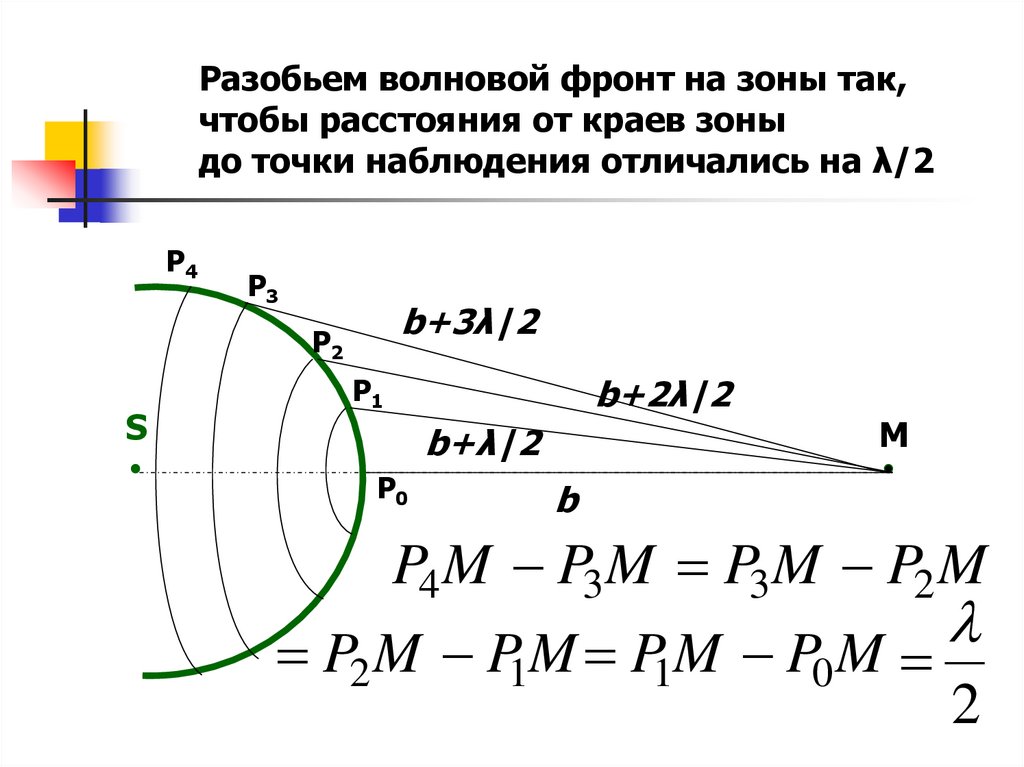
Разобьем волновой фронт на зоны так,
чтобы расстояния от краев зоны
до точки наблюдения отличались на λ/2
Р4
Р3
b+3λ|2
Р2
S
b+2λ|2
Р1
b+λ|2
Р0
M
b
P4 M P3M P3M P2 M
P2 M P1M P1M P0 M
2

3.

Колебания от соседних зон приходят в
точку М в противофазе
A A1 A2 A3 A4
Аi - амплитуда i зоны
Am 1 Am 1
Am
2
A1 A3
A2
2
A1 A1
A3 A3
A5
A A2
A4
2 2
2 2
2
Am A1
2
2

4.

Амплитуда, создаваемая в точке М
сферической волновой поверхностью,
равна половине амплитуды,
создаваемой одной центральной
зоной

5.

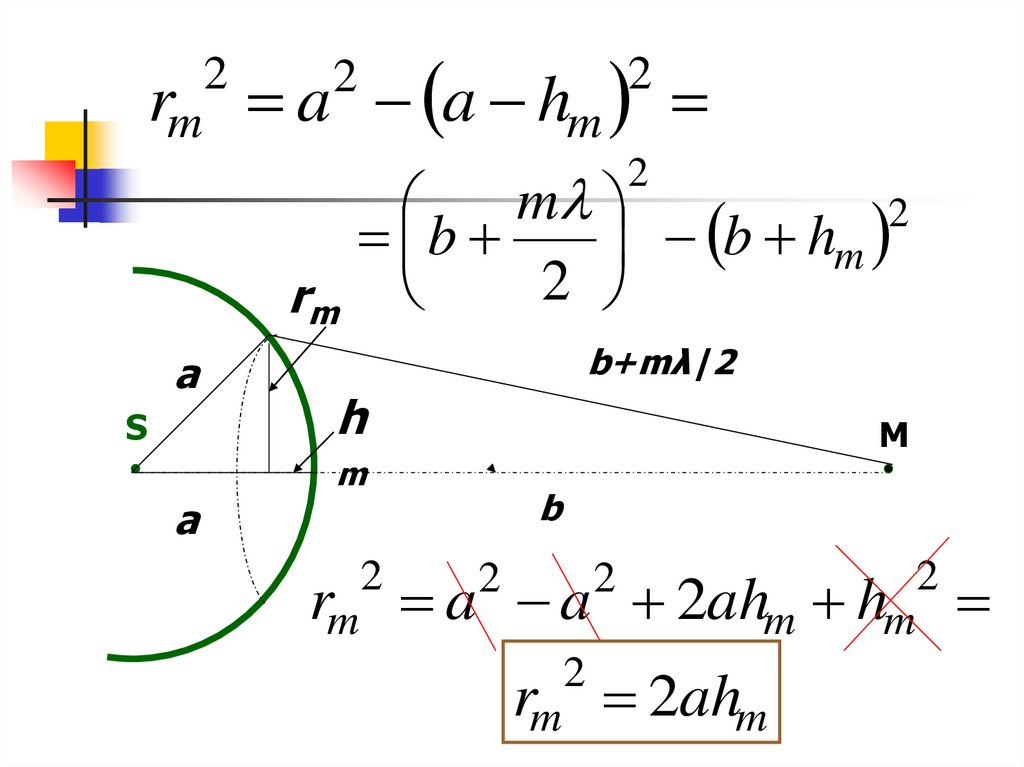
Найдем радиусы зон Френеля

6.

rm a a hm
2
2
2
m
2
b
b hm
2
rm
2
a
S
a
b+mλ|2
h
M
m
b
rm a a 2ahm hm
2
2
2
rm 2ahm
2
2

7.

a a 2ahm hm2
2
2
m
b 2bm
2
(a b)hm bm
2
2
2
bh
b
m hm
2 2
2
hm
2a bm
rm 2ahm
2(a b)
2
2
bm
2(a b)
ab
rm
m
( a b)
радиус внешней границы m зоны Френеля

8.

a – расстояние от источника
до волновой поверхности
b - расстояние от волновой
поверхности до точки
наблюдения

9.

ПРИМЕР
a b 10 см 0,5 мкм
r1 0,158 мм
Распространение света от источника S к точк
происходит так, будто свет распространяется
вдоль очень узкого канала, т.е ПРЯМОЛИНЕЙН
Принцип Гюйгенса-Френеля
объясняет прямолинейное распространение

10.

Если источник
света находится на
бесконечности
(плоская волна)
rm bm
a

11.

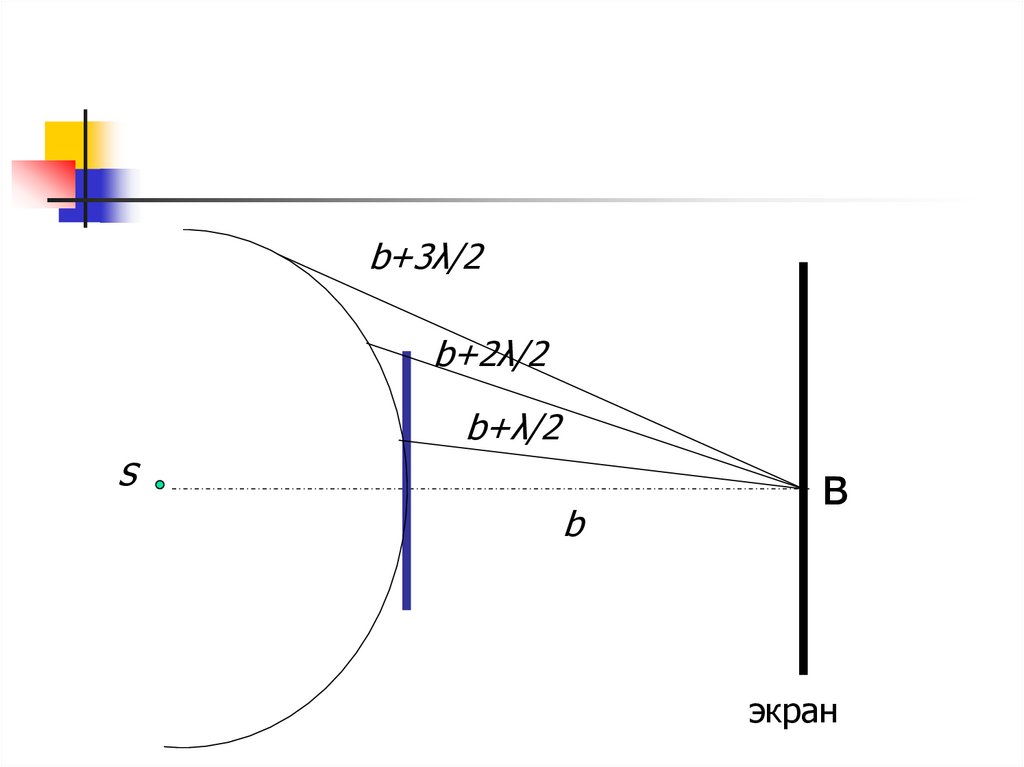
Дифракция
на круглом
диске

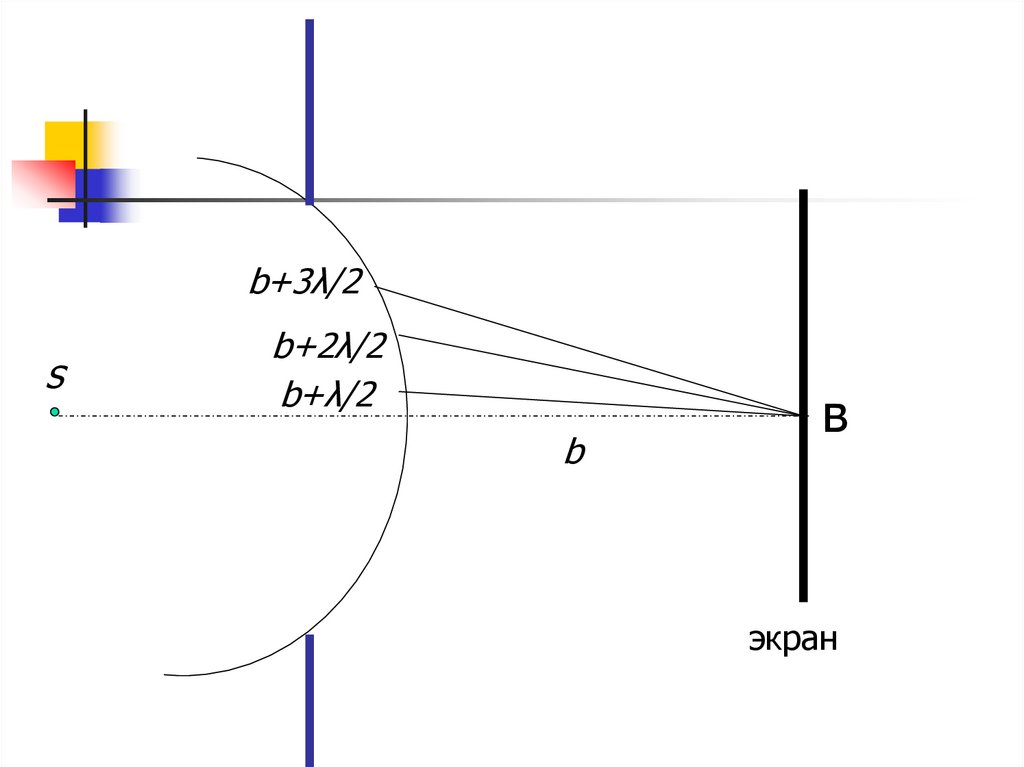
12.

b+3λ/2
b+2λ/2
s
b+λ/2
b
в
экран

13.

Пусть диск закрывает m зон
Френеля
A Am 1 Am 2 Am 3
Am 1 Am 1
Am 3
Am 2
2
2
2
Am 1
В точке В наблюдается
2
светлое пятно

14.

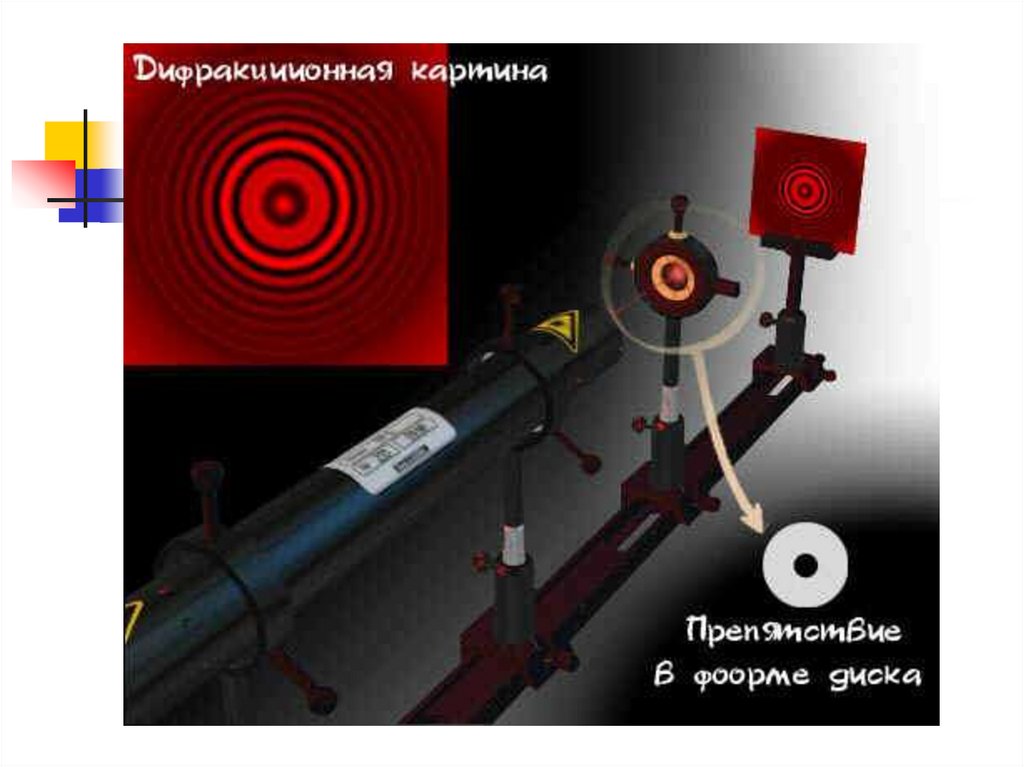
В центре геометрической тени за
диском всегда наблюдается
светлое пятно
Его называют пятном Пуассона

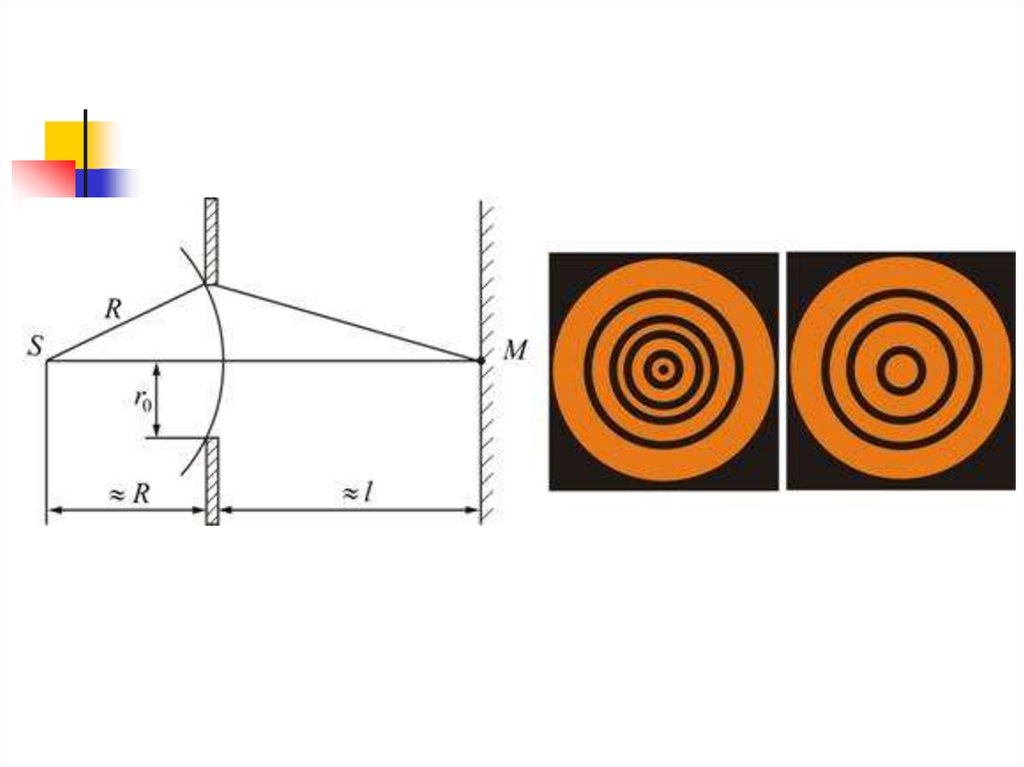
15.

16.

ДИФРАКЦИЯ
ФРЕНЕЛЯ НА
КРУГЛОМ
ОТВЕРСТИИ

17.

b+3λ/2
s
b+2λ/2
b+λ/2
b
в
экран

18.

A1 Am
A
2
2
Знак + соответствует нечетным m
Знак - соответствует четным m

19.

Когда отверстие открывает нечетное
количество зон Френеля, то интенсивность в
точке В будет больше, чем при свободном
распространении волны
Если отверстие открывает четное
количество зон Френеля, то интенсивность в
точке В будет равна 0 (темное пятно)
В центре дифракционной картины (точка M)
может быть как светлое, так и темное
пятно

20.

21.

ДИФРАКЦИЯ
ФРАУНГОФЕРА
НА ОДНОЙ
ЩЕЛИ

22.

Дифракция Фраунгофера –
дифракция плоских волн
(источник расположен на
бесконечности)

23.

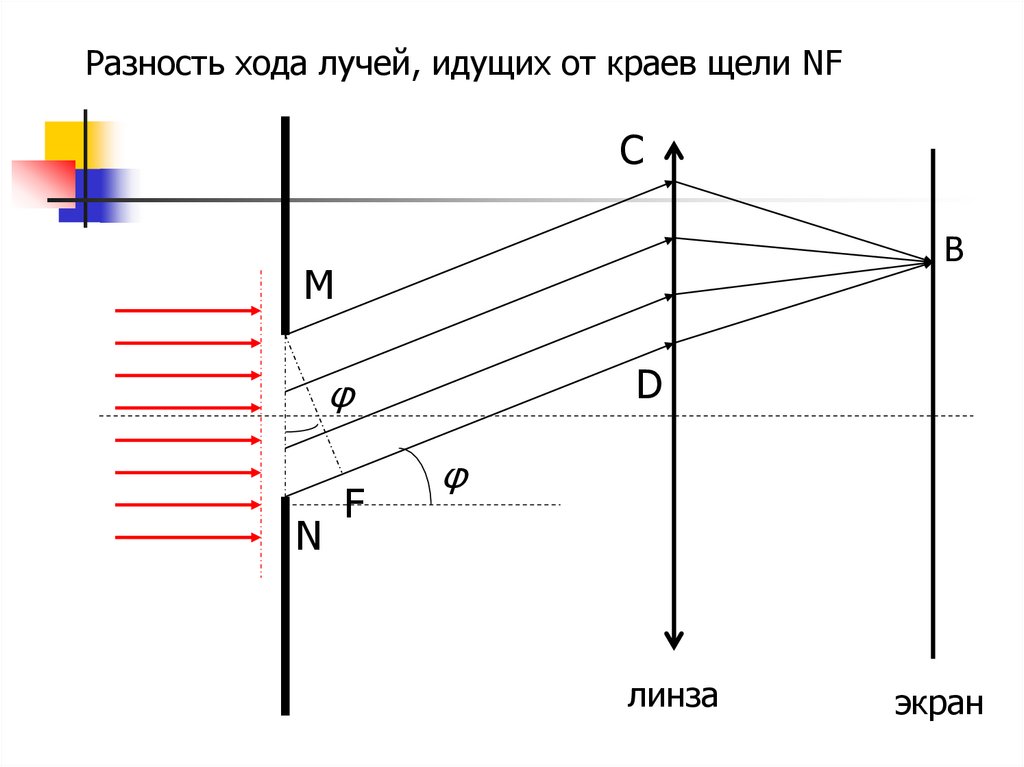
Разность хода лучей, идущих от краев щели NF
C
В
M
D
φ
N
F
φ
линза
экран

24.

Разобьем мысленно щель на зоны
Френеля , имеющие вид полос
Разность хода от краев зоны λ/2
Амплитуды вторичных волн будут
равны между собой
При интерференции волн от
соседних зон они гасят друг
друга

25.

Пусть ширина щели a
NF 1 a sin
Если число зон Френеля четное –
наблюдается дифракционный минимум,
так как волны от соседних зон
гасят друг друга
a sin 2m ,
2
m 1,2,3

26.

Если число зон Френеля нечетное –
наблюдается дифракционный максимум
a sin (2m 1) ,
2
m 1,2,3

27.

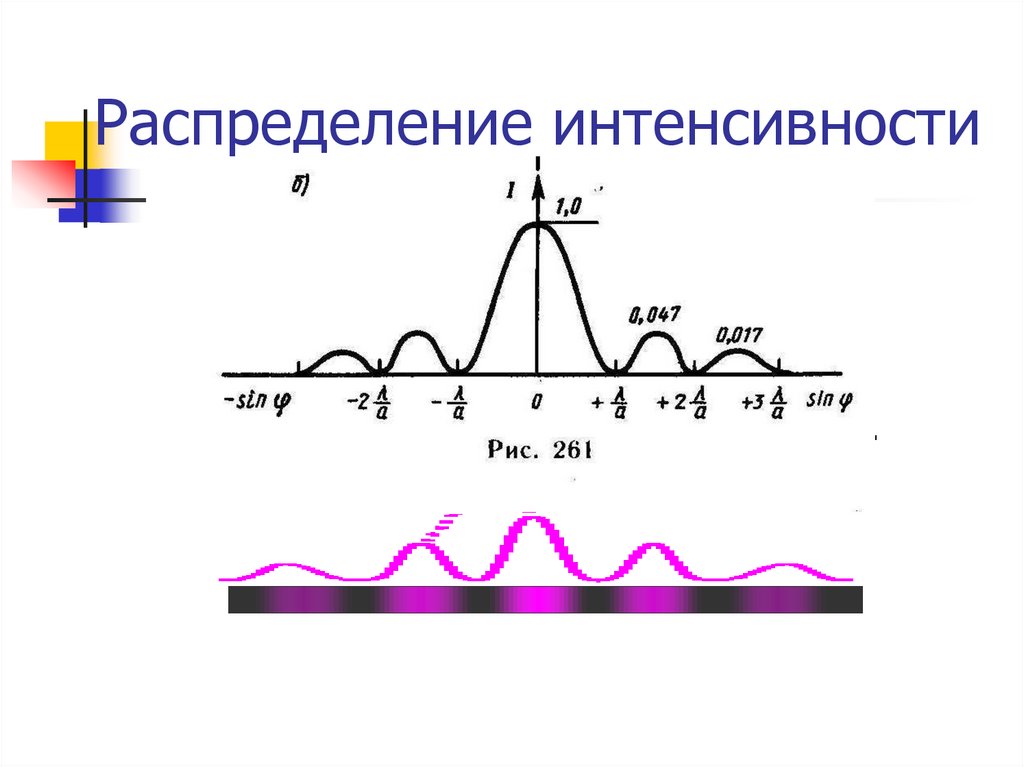
Распределение интенсивности

28.

При освещении щели белым светом
центральный максимум имеет вид
белой полосы
Боковые максимумы разлагаются в
спектр
К центру ближе находится
фиолетовая полоса

29.

ДИФРАКЦИЯ
ФРАУНГОФЕРА НА
ДИФРАКЦИОННОЙ
РЕШЕТКЕ

30.

Дифракционная решетка – система
параллельных щелей равной ширины,
разделенных между собой
непрозрачными промежутками

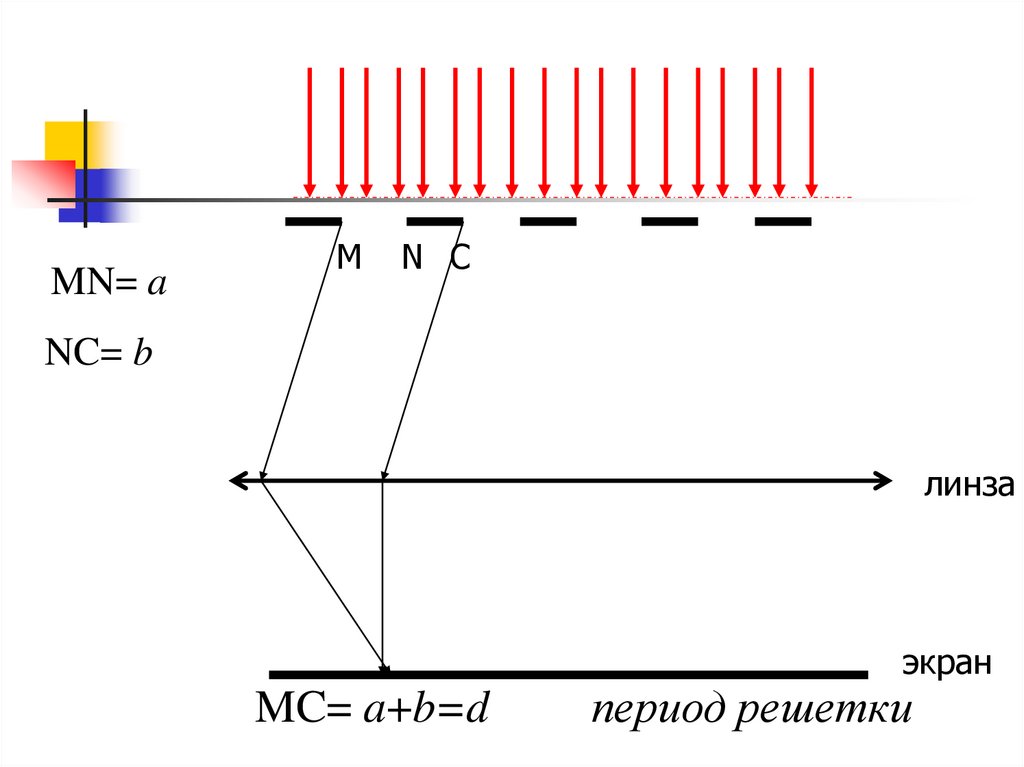
31.

MN= a
M
N C
NC= b
линза
экран
MC= a+b=d
период решетки

32.

Главные максимумы
Появляются в тех
направлениях, где
лучи от соседних
щелей усиливают
друг друга
вследствие
интерференции
d sin m

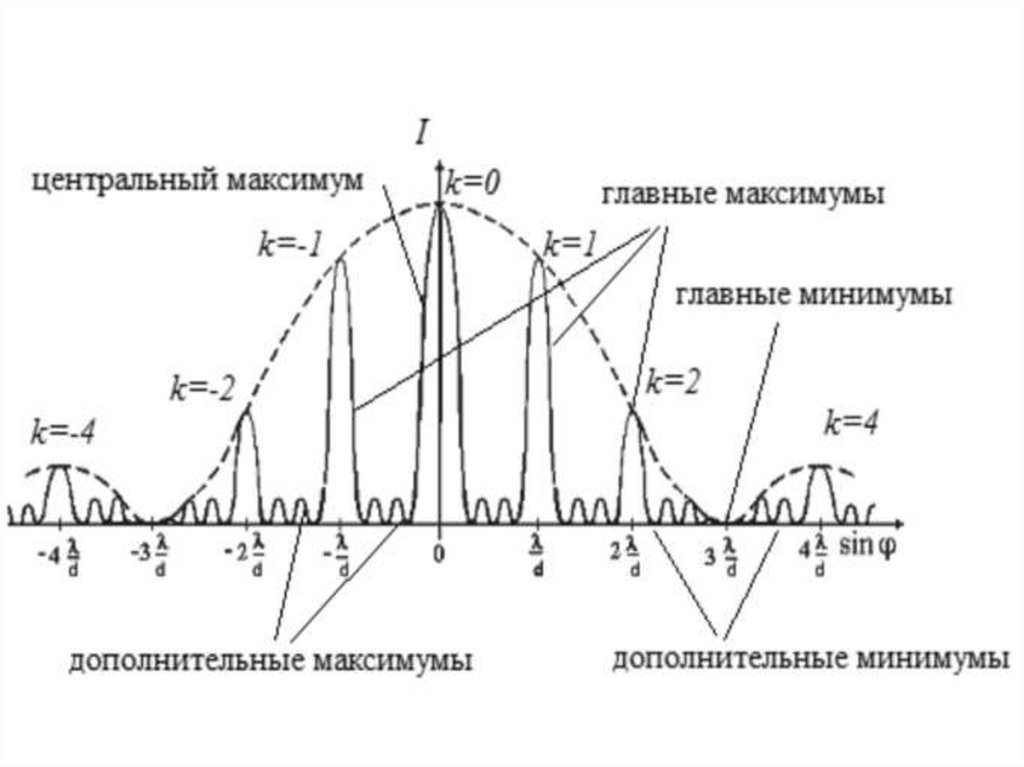
33.

При k 0 наблюдается
центральный максимум
По обе стороны от
центрального максимума
располагаются главные
максимумы 1 порядка, 2
порядка и т.д.
Количество главных
максимумов ограничено

34.

d sin m
Условие главных максимумов
(sin ) max 1
d
mmax
- максимальный порядок спектра
-Наибольший номер
главного максимума
N max 2mmax 1 - количество главных максимумов

35.

В тех направлениях, где одна щель
дает минимум , то и другая щель
также дает минимум
Эти минимумы называются главными
Появляются в тех направлениях, где лучи
от соседних щелей гасят друг друга
вследствие интерференции

36.

Условие главных минимумов
a sin m

37.

Между главными максимумами
расположены дополнительные
максимумы и минимумы
Их количество определяется числом
щелей в дифракционной решетке N
N-2 дополнительных максимума
между двумя соседними главными
максимумами
N-1 дополнительных минимума между
двумя соседними главными
максимумами

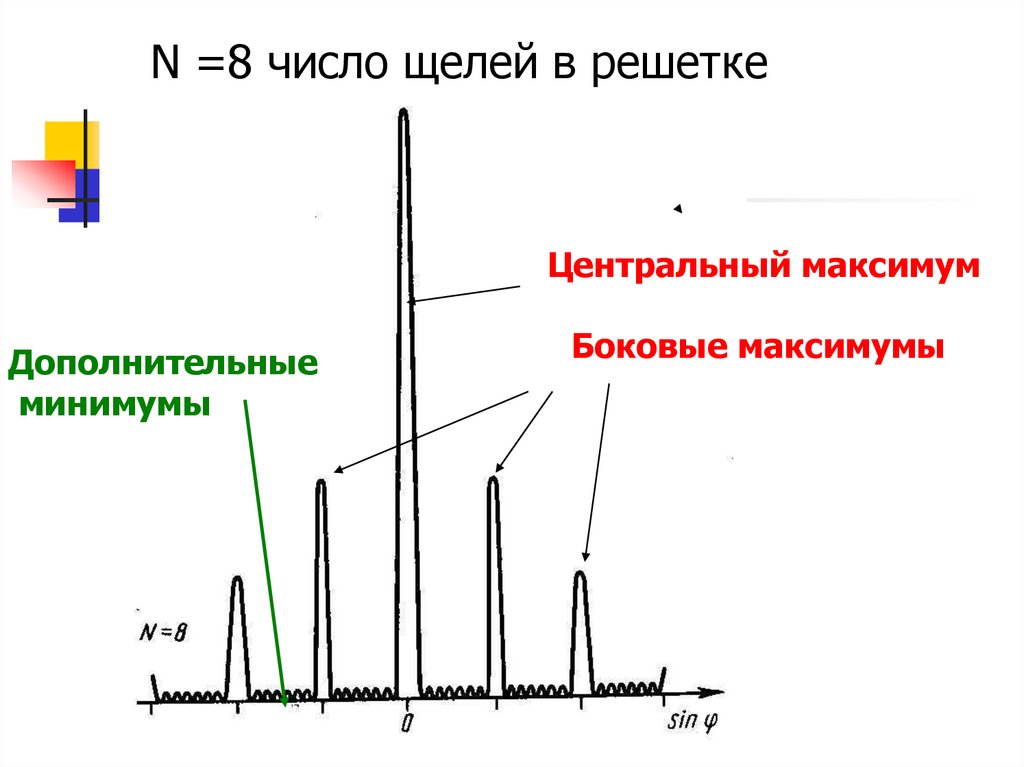
38.

N =8 число щелей в решетке
Центральный максимум
Дополнительные
минимумы
Боковые максимумы

39.

Иногда условие главного максимума
дифракционной решетки может
совпадать с условием минимума от
щели
Это может привести к исчезновению
некоторых главных максимумов

40.

Появляются в тех направлениях, где лучи
от соседних щелей гасят друг друга
вследствие интерференции
Между двумя главными максимумами
располагается (N-1) дополнительный
минимум
d 3a
Исчезает каждый третий главный максимум

41.

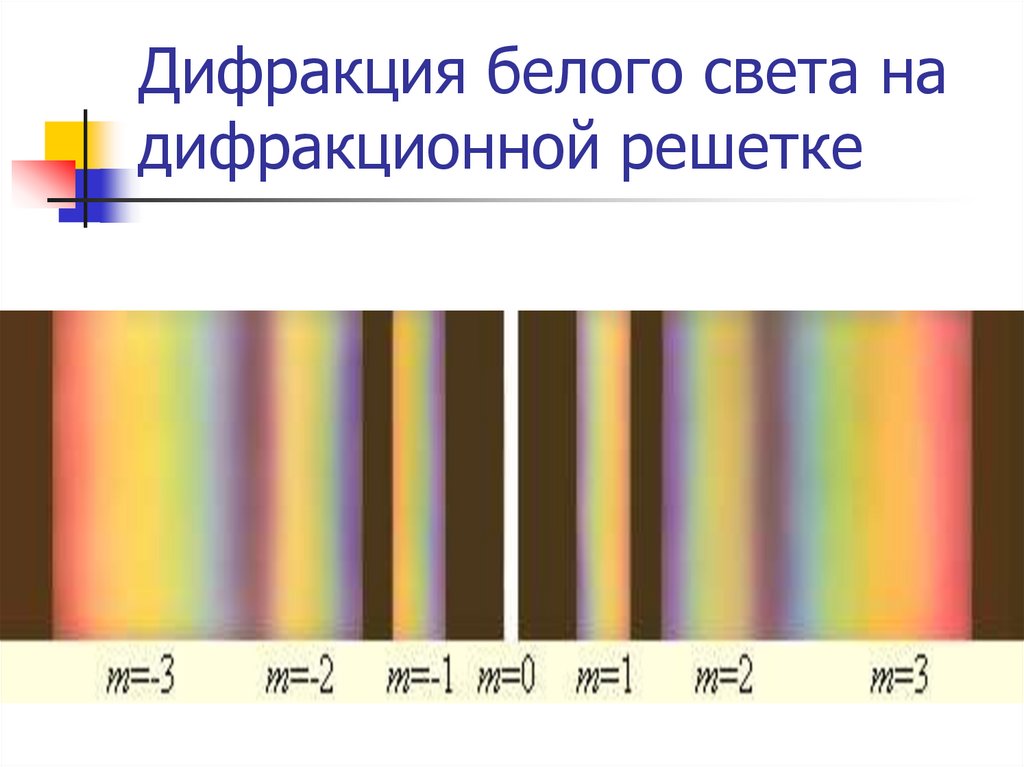
42.

Дифракция белого света на
дифракционной решетке