Этапы коммерциализации проекта

1.

Этапы коммерциализации проекта

2. Элементы финансовых расчетов

К основным понятиям финансовой математики относятся:
P – первоначальная инвестированная сумма,
S - наращенная сумма,
n - период начисления — промежуток времени, за который начисляются
проценты, измеряется в годах,
m - количество интервалов начисления в каждом году - минимальный
промежуток времени, по прошествии которого происходит начисление
процентов.
2/8

3. Элементы финансовых расчетов

Процентная ставка — величина, которая характеризует интенсивность
начисления процентов. Ставки всегда годовые.
Различают
2
способа
начисления
процентов:
декурсивный
антисипативный.
Декурсивная процентная ставка i называется ссудной.
Антисипативная процентная ставка d называется учетной ставкой.
и
В обоих способах начисления процентов процентные ставки могут быть
простыми, либо сложными.
3/8

4. Простая ссудная ставка

После 1го года
S = Р + iP = Р(1 + i)
После 2х лет
S = Р + iP + iP = Р(1 + 2i)
После n лет
S = Р(1 + ni)
4/8

5. Сложная ссудная ставка

После 1го года
S = Р + iP = Р(1 + i)
После 2х лет
S = Р(1 + i) + iP(1+i) = Р(1 + i)(1 + i) = P(1+i)2
После n лет
S = P(1+i)n
5/8

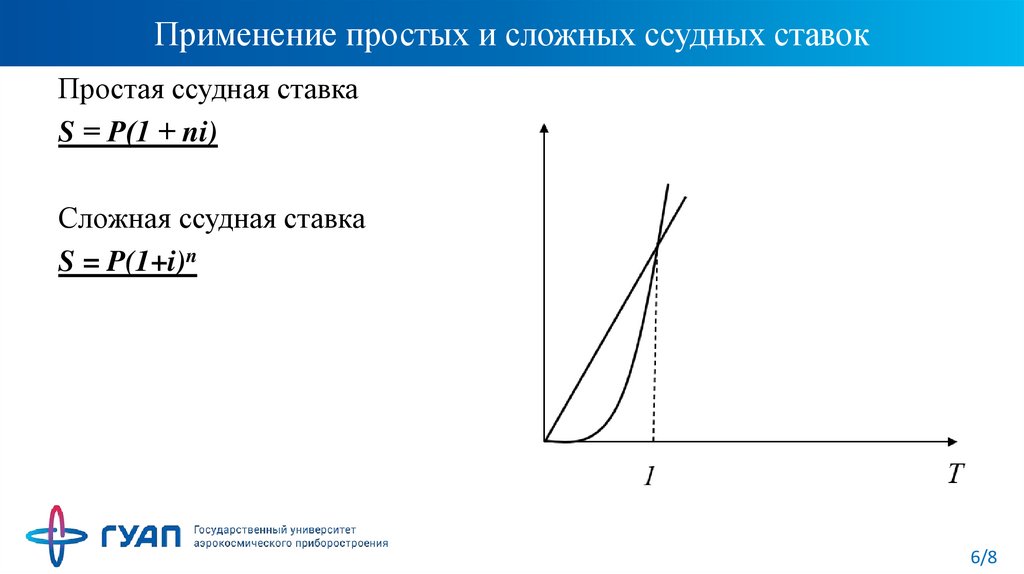
6. Применение простых и сложных ссудных ставок

Простая ссудная ставка
S = Р(1 + ni)
Сложная ссудная ставка
S = P(1+i)n
6/8

7. Когда период меньше года

n = t/T, где
t — период начисления (в днях),
T — продолжительность года (в днях)
Дата выдачи и дата погашения ссуды всегда считаются за один день.
360/360 - обыкновенные проценты с приближенным числом дней
ссуды
365/365 - точные проценты с точным числом дней ссуды
365/360 - называются обыкновенные проценты с точным числом
дней ссуды
7/8

8. Пример

Первоначальная сумма 3000 у.е. помещена в банк под 12% годовых, проценты
простые ссудные, на срок с 22 мая по 24 декабря того же года. Определить
наращенную сумму в каждой из практик начисления процентов. t: 22.05 – 24.12
Решение:
t360 = 10 (май) + 6*30 (июнь, июль, август, сентябрь, октябрь, ноябрь) + 24
(декабрь) - 1 (день открытия и день закрытия счета считаются за один день) = 213
дней.
t365 = 10 (май) + 30 (июнь) + 31 (июль) + 31 (август) + 30 (сентябрь) + 31 (октябрь)
+ 30 (ноябрь) +24 (декабрь) - 1 (день открытия и день закрытия счета считаются
за один день) = 216 дней
S360/360 = Р(1 + it/Т) = 3000*(1 + 0,12*213/360) = 3213 у.е.
S365/360 = Р(1 + it/Т) = 3000*(1 + 0,12*216/360) = 3216 у.е.
S365/365 =Р(1 + it/T) = 3000*(1 + 0,12*216/365) = 3213,04 у.е.
8/8

9. Погашение задолженности частями

Необходимым условием финансовой или кредитной операции в любой ее форме
является сбалансированность вложений и отдачи. Понятие сбалансированности
удобно пояснить на графике
9/8

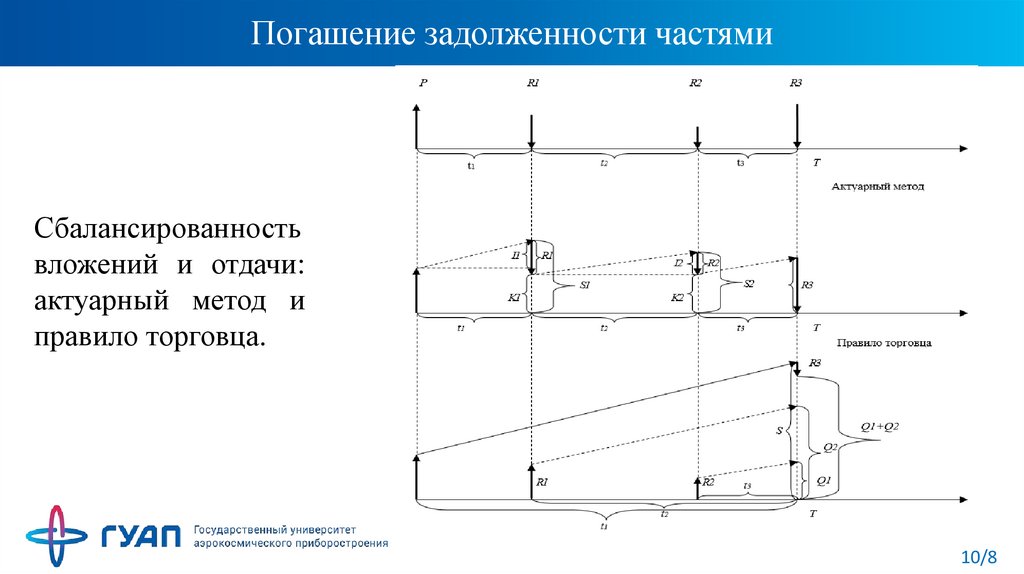
10. Погашение задолженности частями

Сбалансированность
вложений и отдачи:
актуарный метод и
правило торговца.
10/8

11. Актуарный метод

К1 = Р(1 + t1i) – R1, если I1 ≤ R1
K2 = K1(1 + t2i) – R2, если I2 ≤ R2
K2(1 + t3i) – R3 = 0, т.е. R3 = K2(1 + t3i)
11/8

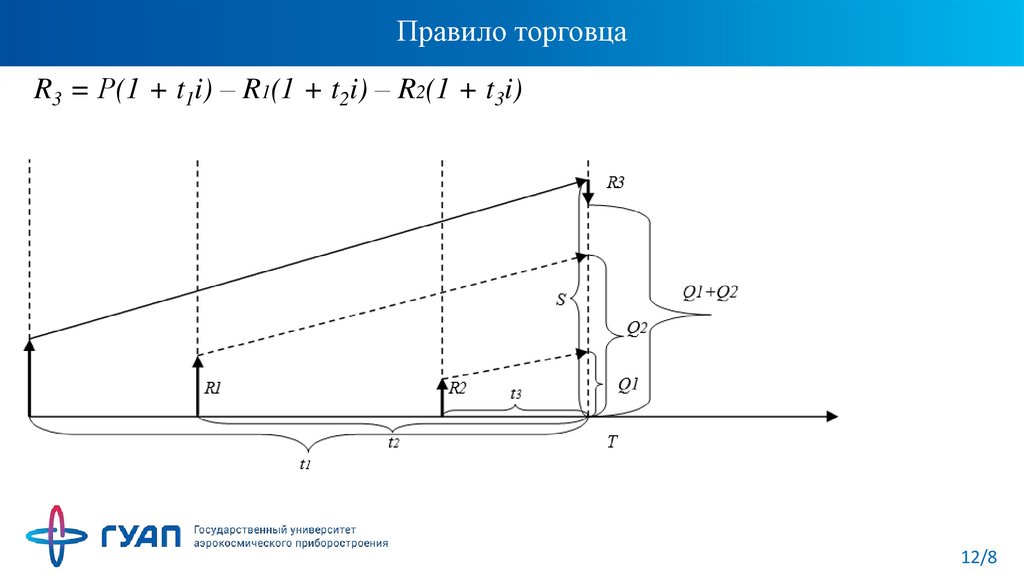
12. Правило торговца

R3 = Р(1 + t1i) – R1(1 + t2i) – R2(1 + t3i)
12/8

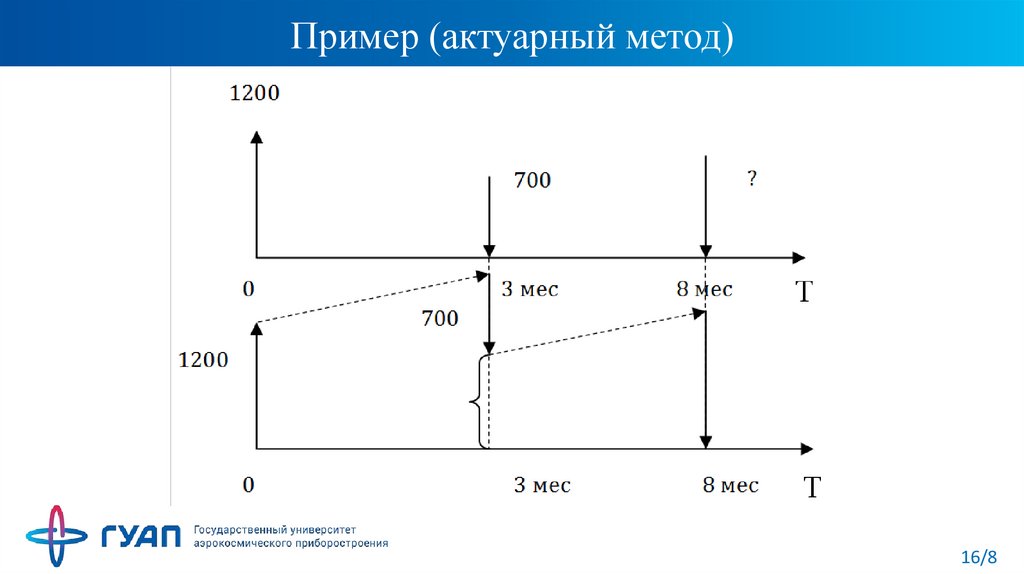
13. Пример

Обязательство в 1200 у.ед. должно быть погашено через 8
месяцев. В счет выплаты долга через 3 месяца поступило
700 у.ед. Определить остаток долга, если на него
начисляются
проценты по ставке 20% годовых.
(актуарным методом и правилом торговца).
13/8

14. Пример

Обязательство в 1200 у.ед. должно
быть погашено через 8 месяцев. В
счет выплаты долга через 3 месяца
поступило 700 у.ед. Определить
остаток долга, если на него
начисляются проценты по ставке
20% годовых. (актуарным методом и
правилом торговца).
14/8

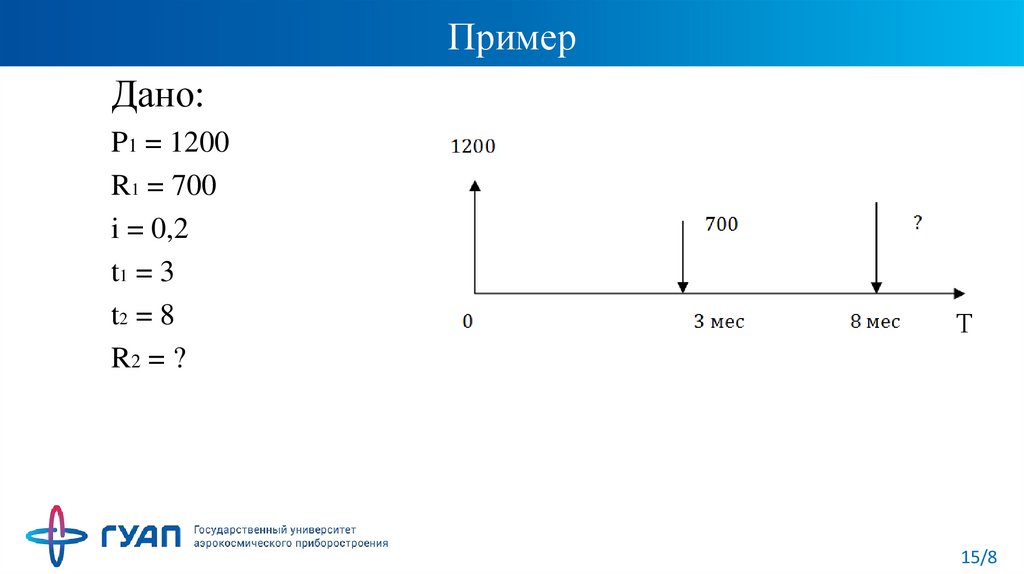
15. Пример

Дано:
P1 = 1200
R1 = 700
i = 0,2
t1 = 3
t2 = 8
R2 = ?
15/8

16. Пример (актуарный метод)

16/8

17. Пример (актуарный метод)

17/8

18. Пример (актуарный метод)

18/8

19. Пример (правило торговца)

19/8

20. Пример (правило торговца)

20/8

21. Антисипативные ставки. Вексель.

Сумма получаемого дохода рассчитывается исходя из наращенной суммы S
(величины погашаемого кредита). Заемщик получает в начале периода
начисления процентов сумму Р = S - D, где D - это дисконт (скидка) Такая
операция называется дисконтированием по простой учетной ставке. На практике
учетные ставки применяются при учете (покупке) векселей.
Если d — простая учетная ставка, то
P = S(1 - nd)
S = Р(1 + ni)
Если d — сложная учетная ставка, то
P = S(1 -d)n
S = Р(1 + i)n
21/8

22. Антисипативные ставки. Вексель.

ПРИМЕР
Погасительный платеж суммой 500 у.е. по кредитному договору должен быть
внесен через 8 месяцев. Определить сумму полученного кредита, если:
1) Кредит предоставлен по простой судной процентной ставке 20% годовых
2) Кредит предоставлен в виде векселя по простой учетной ставке 20% годовых
1) S = Р(1 + ni), т.е. P = S/(1 +ni) = 500/(1 + 0,2*8/12) = 441 у.е.
2) P = S(1 - nd) = 500(1 – 0,2*8/12) = 433 у.е.
22/8

23. Эквивалентность ставок.

Часто перед инвестором стоит задача выбора одного из этих вариантов
инвестирования первоначальной суммы. Возникает задача сравнения между
собой различных процентных ставок.
Две ставки называются эквивалентными, если при одинаковой
первоначальной сумме Р и за одинаковый период начисления п они приводят к
одинаковой наращенной сумме S.
При сравнении двух ставок из разных классов для одной из них находят
эквивалентную ей ставку из другого класса и проводят сравнение двух ставок из
одного класса.
23/8

24. Эквивалентность ставок.

Определим сложную ссудную ставку эквивалентную сложной номинальной
ставке.
Начисление сложных процентов может происходить несколько раз в году. В этом
случае указывают номинальную процентную ставку j, на основании которой
рассчитывают процентную ставку для каждого интервала начисления.
Определим сложную ссудную ставку эквивалентную сложной номинальной
ставке.
S1 = Р(1 + iс)n
S2 = Р(1 + j/m)nm
)nm
24/8

25. Эквивалентность ставок.

Определим сложную ссудную ставку эквивалентную сложной номинальной
ставке.
S1 = Р(1 + iс)n
S2 = Р(1 + j/m)nm
Так как ставки эквивалентны, то
S1 = S2= S
P1 = P2 = P
n1 = n2 = n
то есть Р(1 + iс)n = Р(1 + j/m)nm
Следовательно (1 + iс)n = (1 + j/m)nm
=> ic = (1 + j/m)m – 1 - эффективная ставка
25/8

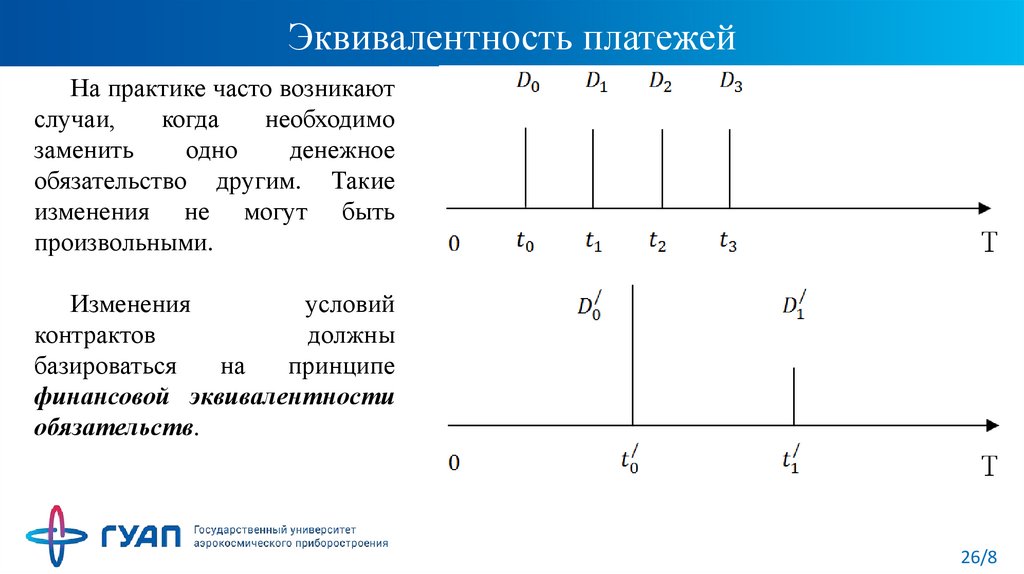
26. Эквивалентность платежей

На практике часто возникают
случаи,
когда
необходимо
заменить
одно
денежное
обязательство другим. Такие
изменения не могут быть
произвольными.
Изменения
условий
контрактов
должны
базироваться
на
принципе
финансовой эквивалентности
обязательств.
26/8

27. Эквивалентность платежей

Эквивалентными считаются такие платежи, которые, будучи приведенными к
одному общему моменту времени, оказываются равными.
Для краткосрочных обязательств приведение осуществляется обычно на основе простых ставок,
для средне- и долгосрочных - с помощью сложных процентных ставок.
Целесообразно обозначать каждый платеж переменной D.
Одним из распространенных случаев изменения условий контрактов является консолидация
(объединение) платежей. Пусть платежи D1, D2,..., Dm со сроками n1, n2,…,nm заменяются одним в
сумме D0 и сроком n0. В этом случае возможны две постановки задачи: если задается срок n0, то
находится сумма D0 и наоборот, если задана сумма консолидированного платежа D0, то определяется
срок n0.
27/8

28. Эквивалентность платежей

D0
n0 = ?
28/8

29. Эквивалентность платежей

D0
n0 = ?
В
случае
краткосрочных
уравнение эквивалентности:
платежей
следовательно
29/8

30. Эквивалентность платежей

D0
n0 = ?
В случае долгосрочных платежей уравнение
эквивалентности:
обозначим
тогда
30/8

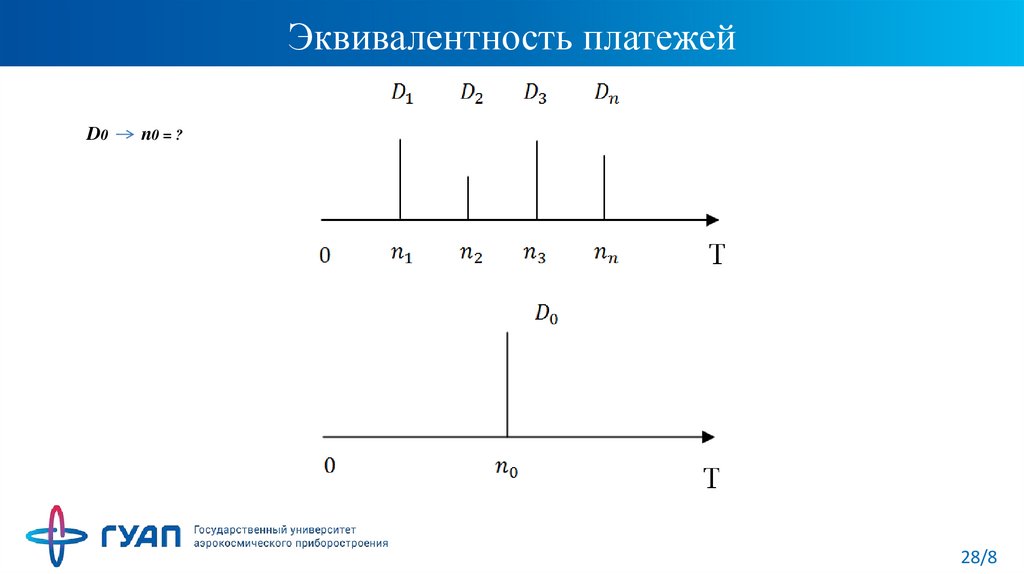
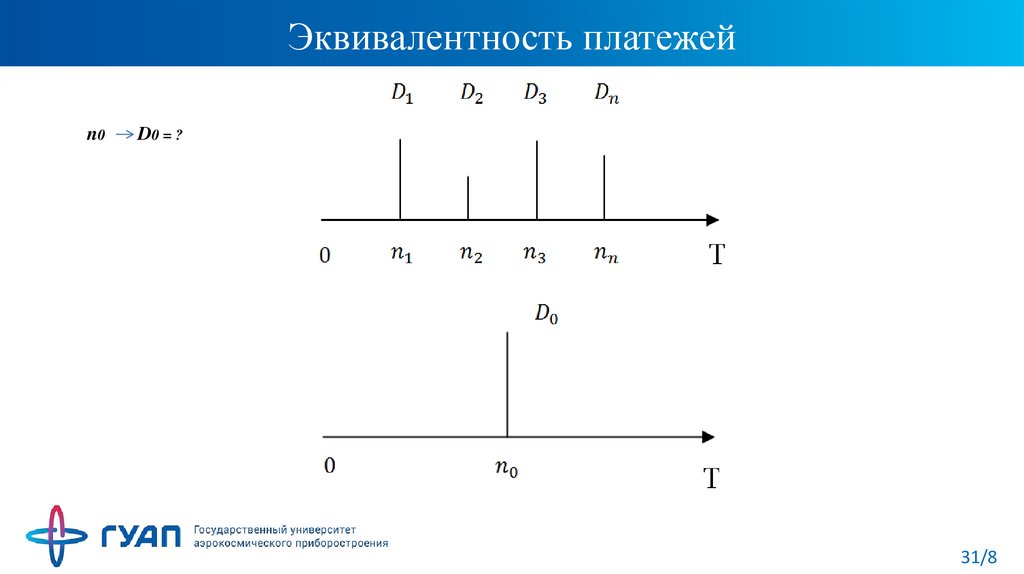
31. Эквивалентность платежей

n0
D0 = ?
31/8

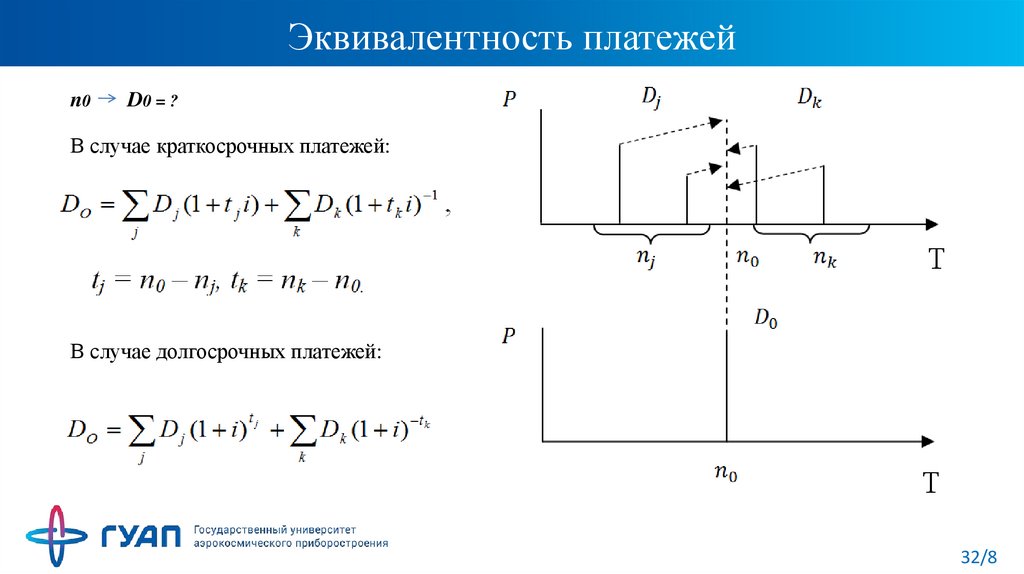
32. Эквивалентность платежей

n0
D0 = ?
В случае краткосрочных платежей:
В случае долгосрочных платежей:
32/8

33. ПРИМЕР

По договору платежи в
размере 100 и 500 у.е. должны
состояться через 3 года и 6
лет
соответственно.
Определить
размер
заменяющего платежа через 5
лет, если условия контракта
20% годовых.
Дано:
D1 = 100 у.е.
D2 = 500 у.е.
n1 = 3 года
n2 = 6 лет
n’ = 5 лет
i = 20%
Найти: D’ = ?
33/8

34. ПРИМЕР

Дано:
D1 = 100 у.е.
D2 = 500 у.е.
n1 = 3 года
n2 = 6 лет
n’ = 5 лет
i = 20%
Найти: D’ = ?
34/8

35. ПРИМЕР

35/8

36. Влияние инфляции на финансовые операции

S — это сумма денег, для которой рассматривается покупательная
способность при отсутствии инфляции.
Sα — это сумма денег, покупательная способность которой с
учетом инфляции равна покупательной способности суммы S при
отсутствии инфляции
Обозначим ΔS = Sα – S,
тогда уровень (темп) инфляции
Показывает, на сколько процентов в среднем выросли цены за
период.
36/8

37. Влияние инфляции на финансовые операции

Величину
называют индексом инфляции. Это индекс роста,
показывает, во сколько раз в среднем выросли цены за
рассматриваемый период.
37/8

38. ПРИМЕР

Уровень инфляции в месяц составил 2%. Каков уровень
инфляции за год?
Дано:
38/8

39. ПРИМЕР

Уровень инфляции в месяц составил 2%. Каков уровень
инфляции за год?
39/8

40. Учет инфляции в краткосрочных операциях

40/8

41. Учет инфляции в краткосрочных операциях

41/8

42. Учет инфляции в краткосрочных операциях

42/8

43. ПРИМЕР

Ежемесячный уровень инфляции 1,5%. Под какую ставку нужно
инвестировать на 6 месяцев, чтобы обеспечить реальную
доходность 6% годовых?
Дано:
43/8

44. ПРИМЕР

44/8

45. Учет инфляции в долгосрочных операциях

45/8

46. Учет инфляции в долгосрочных операциях

46/8

47. ПРИМЕР

Период начисления 3 года, ожидаемый ежемесячный
уровень инфляции 0,5%. Под какую минимальную
ставку ссудного процента нужно инвестировать,
чтобы обеспечить реальную доходность 10%
годовых?
47/8

48. ПРИМЕР

Дано:
48/8

49. ПРИМЕР

49/8

50. ПРИМЕР

50/8