Похожие презентации:
Урок 12. Числовые характеристики распределения дискретных и непрерывных случайных величин
1. Урок 12.
Числовые характеристикираспределения дискретных и
непрерывных случайных величин.
2.
Числовые параметры, которые всжатой форме выражают наиболее
важные черты распределения,
называются числовыми
характеристиками случайной
величины.
3. Математическое ожидание.
Математическое ожидание служитдля характеристики особенности
распределения СВ, если ее возможные
значения сосредоточены вокруг
некоторого центра (центр
распределения или среднее значение
СВ).
4. Определение.
Математическим ожиданием МХдискретной СВ называется сумма
произведений возможных значений
СВ на соответствующие вероятности.
n
МХ xi pi
i 1
5. Задача 1.
Дискретная величина задана рядомраспределения:
Х
2
5
8
19
Р
0,2
0,3
0,4
0,1
МХ=2*0,2+5*0,3+8*0,4+19*0,1=7
6. Математическое ожидание НСВ:
вМХ х f ( x)dx
а
7. Задача 2.
x 1;0,
f ( x) x 1, 1 x 2;
0,
x 2.
2
2
3
2
x
x
2
2
MX x ( x 1)dx ( x x)dx ( )1
3
2
1
1
8
1 1
7 3 5
( 2) ( ) .
3
3 2
3 2 6
8. Определение.
Две СВ называются независимыми,если закон распределения
вероятности одной из них не зависит
от того, какие возможные значения
приняла другая величина.
9. Свойства математического ожидания:
М(Х+Y)=М(Х)+М(Y);М(Х-Y)=М(Х)-М(Y);
Для независимых величин
М(Х*Y)=М(Х)*М(Y);
МС=С;
М(СХ)=С(МХ);
М(Х-МХ)=0, где (Х-МХ) – отклонение
СВ от ее математического ожидания.
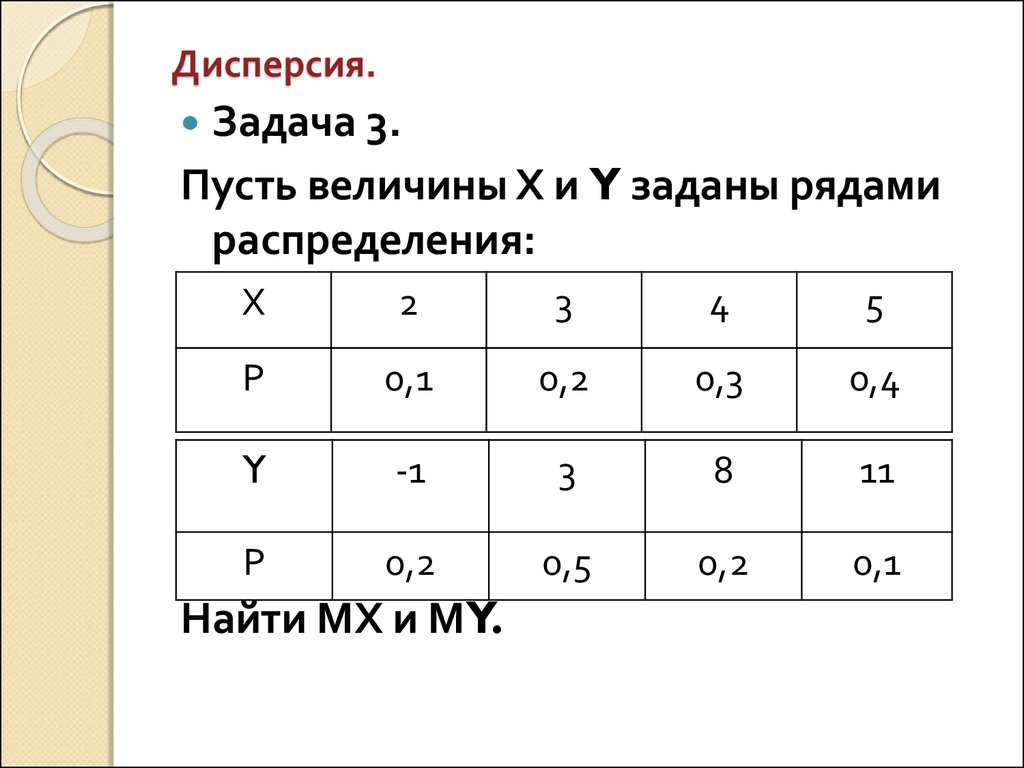
10. Дисперсия.
Задача 3.Пусть величины Х и Y заданы рядами
распределения:
Х
2
3
4
5
Р
0,1
0,2
0,3
0,4
Y
-1
3
8
11
Р
0,2
0,5
0,2
0,1
Найти МХ и МY.
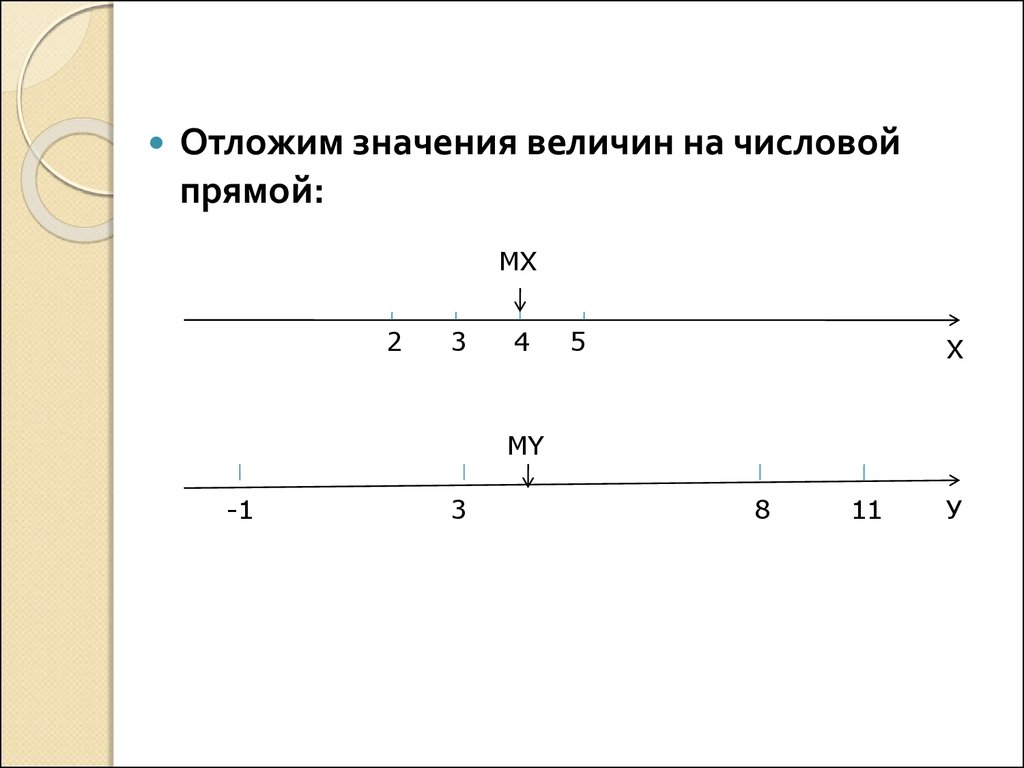
11.
Отложим значения величин на числовойпрямой:
MX
2
3
4
5
Х
MY
-1
3
8
11
У
12.
Определение: Математическоеожидание квадрата отклонения
случайной величины от ее
математического ожидания
называется дисперсией.
2
DX M ( X MX )
n
для ДСВ : DX ( xi MX ) 2 pi
i 1
b
для НСВ : DX ( x MX ) 2 f ( x ) dx
a
13. Среднее квадратическое отклонение
Квадратный корень из дисперсииназывается средним квадратическим
отклонением:
х DX
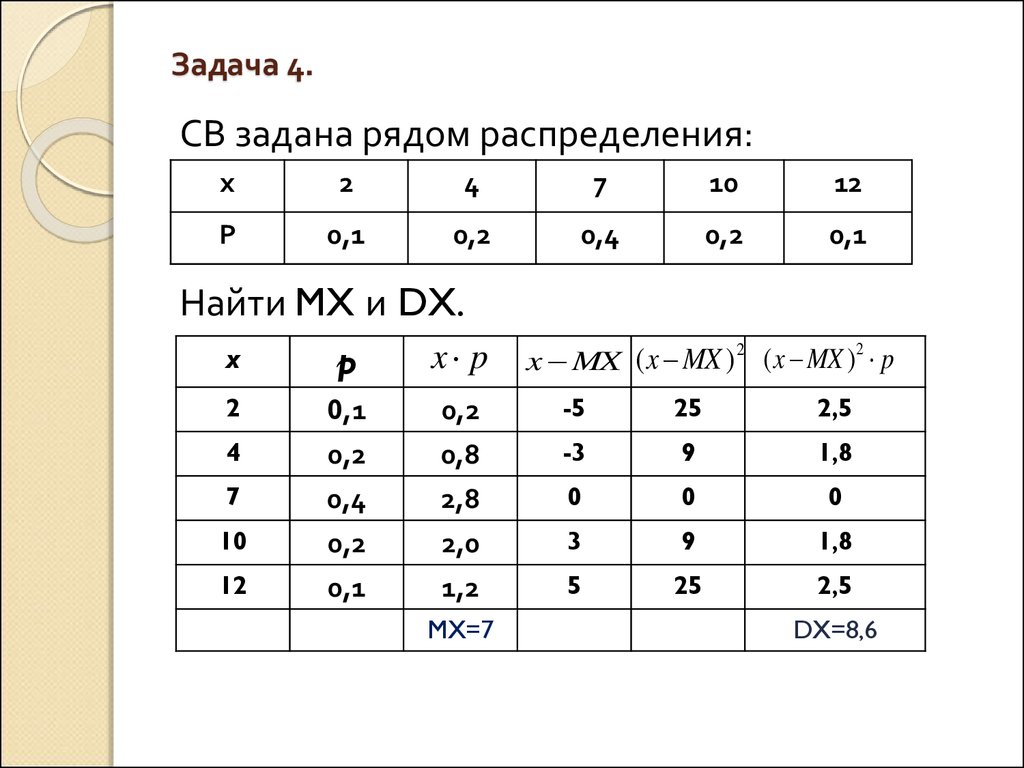
14. Задача 4.
СВ задана рядом распределения:х
2
4
7
10
12
Р
0,1
0,2
0,4
0,2
0,1
Найти MX и DX.
x
p
x p
2
0,1
0,2
-5
25
2,5
4
0,2
0,8
-3
9
1,8
7
0,4
2,8
0
0
0
10
0,2
2,0
3
9
1,8
12
0,1
1,2
5
25
2,5
MX=7
2
2
x MX ( x MX ) ( x MX ) p
DX=8,6
15. Задача 5.
Случайная величина заданадифференциальной функцией
распределения:
0, x 1;
f ( x) 3 x 2 , 1 x 0;
0, x 0
Найти MX и DX .
b
0
4
3
x
MX x f ( x)dx 3 x3dx (
)
4
a
1
0
0
1
3
;
4
0
3 2
3 2 2
2
DX ( x ( )) 3 x dx 3 ( x ) x dx
4
4
1
1
0
5
4
3
3
9
x
3
x
9
x
3 ( x 4 x3 x 2 )dx 3( )
2
16
5 2 4 16 3
1
0
1
0,0375
16. Свойства дисперсии:
1. D( X Y ) D( X ) D(Y )D( X Y ) D( X ) D(Y )
2. DC 0
3. D(CX ) C DX
2
4. DX M ( X 2 ) ( MX ) 2
17. Задача 6.
Вычислить дисперсию ДСВ, используя рядраспределения и свойство 4.
Х
2
3
4
5
6
Р
0,2
0,2
0,3
0,2
0,1
М ( Х 2 ) 4 0,2 9 0,2 16 0,3 25 0,2 36 0,1 16
( МХ )2 (2 0,2 3 0,2 4 0,3 5 0,2 6 0,1)2 14,44
DX 16 14,44 1,56
18. Следствия:
1. D( X MX ) св .1 DX D( MX ) св.2 DX 0 DX2. Z
X MX
x
стандартная величина;
X MX 1
MZ M
M ( X MX ) 0
x x
X MX 1
DX
DZ D
2 D( X MX ) 2 1
x
x x
19. Используя данные задач , найти математическое ожидание и дисперсию СВ:
1. В партии из 8 деталей 5 стандартных.Наудачу взяты 4 детали. Построить ряд
распределения числа стандартных
деталей среди отобранных.
2.
0, x 1;
f ( x) 2( x 1),1 x 2;
0, x 2
Найти MX и DX .






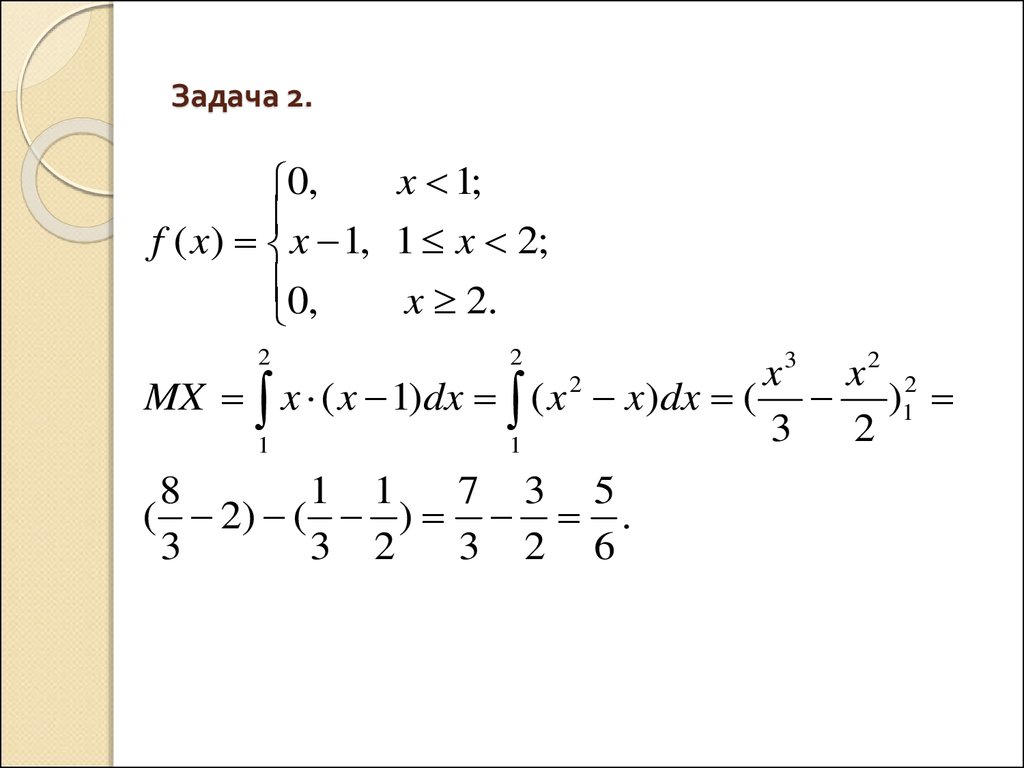









 Математика
Математика








