Похожие презентации:
Чётность, нечётность, периодичность тригонометрических функций (11 класс)
1. 11 класс Алгебра Чётность, нечётность, периодичность тригонометрических функций
Автор презентации:Попов Дмитрий Сергеевич
2. Сегодня на уроке мы будем разбираться со свойствами тригонометрических функций. Будем учиться отличать чётную функцию от
нечётной, узнаем, чтотакое периодичность и где она
встречается.
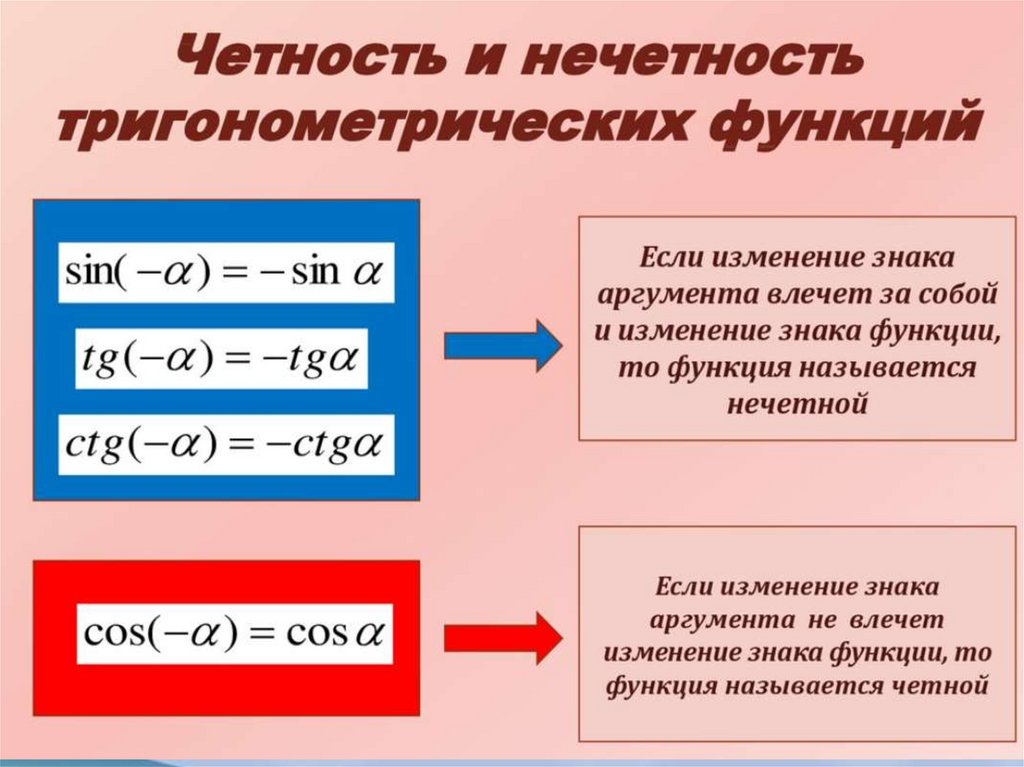
3. ЧЁТНАЯ ФУНКЦИЯ – функция, у которой выполняется равенство f(-x) = f(x), т.е. при противоположных числах значение функции
одинаковое.4. В тригонометрии чётная функция одна – косинус.
у = соs(x) чётная функция,т.к. cоs(-x) = cos(x)
Пример:
5. НЕЧЁТНАЯ ФУНКЦИЯ – функция, у которой выполняется равенство f(-x) = -f(x), т.е. при противоположных числах значение функции
противоположное.6. В тригонометрии y = sin(x), y = tg(x), y = ctg(x) – нечётные функции
т.к. sin(-x) = -sin(x)tg(-x) = -tg(x)
ctg(-x) = -ctg(x)
7.
8. Итак, с чётностью и нечётностью мы разобрались, - здесь всё легко.
Итак, с чётностью инечётностью мы разобрались, здесь всё легко.
А вот с периодом будет чуть сложнее.
У всех разные ассоциации со словом период. В нашем
случае «период» - это период времени.
Например, 1 января наступает каждый год, т.е.
проходит некий период времени и наступает 1 января.
ПЕРИОД ВСЕГДА БУДЕТ ОДИНАКОВЫМ ЧИСЛОМ!
9. Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T
Периодическая функция — это функция, значения которойне изменяются при добавлении к значениям её аргумента
некоторого числа T (отличного от нуля).
Функция y = f(x) называется периодической, если
существует такое число T≠0, что для любого x из
области определения этой функции выполняются
равенства: f (x-T)= f (x) =f (x+T).
Число T называют периодом функции y=f(x).
10. Если х принадлежит области определения функции f(x), то числа x + T, x – T и вообще числа x + Tn, n ∈ Z, также принадлежит
области определения функцииf(x – Tn ) = f(x), n ∈ Z
Исходя из этого мы с вами можем увидеть, что мы можем взять не один период,
а несколько.
Например, представьте, что вы раз в пять лет видитесь со своим другом Денисом,
который живёт в Москве. В данном случае период будет – 5 лет. Вы берёте один год
5 раз. И у вас получается, что, допустим, год спустя вы не увиделись, но через
пять таких годов вы опять встретились.
11. ВСЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЯВЛЯЮТСЯ ПЕРИОДИЧЕСКИМИ!!!
12. ПЕРИОДЫ ФУНКЦИЙ
У каждой тригонометрической функции свой период.13. ЗАДАНИЕ 1 (РЕШИМ ВМЕСТЕ)
Выяснить, является ли данная функция чётной или нечётной14. №702 (4)
Доказать, что функция у = f(x) является периодическойс периодом 2п, если
15. №703 (3)
Доказать, что функция у = f(x) является периодическойс периодом Т, если
16. ДОМАШНЕЕ ЗАДАНИЕ
• Прочитать § 39• Выполнить №700(3,6); 701(3);
№705 (1)















 Математика
Математика








