Похожие презентации:
Чётность, нечётность, периодичность функций
1.
Чётность,нечётность,
периодичность
функций
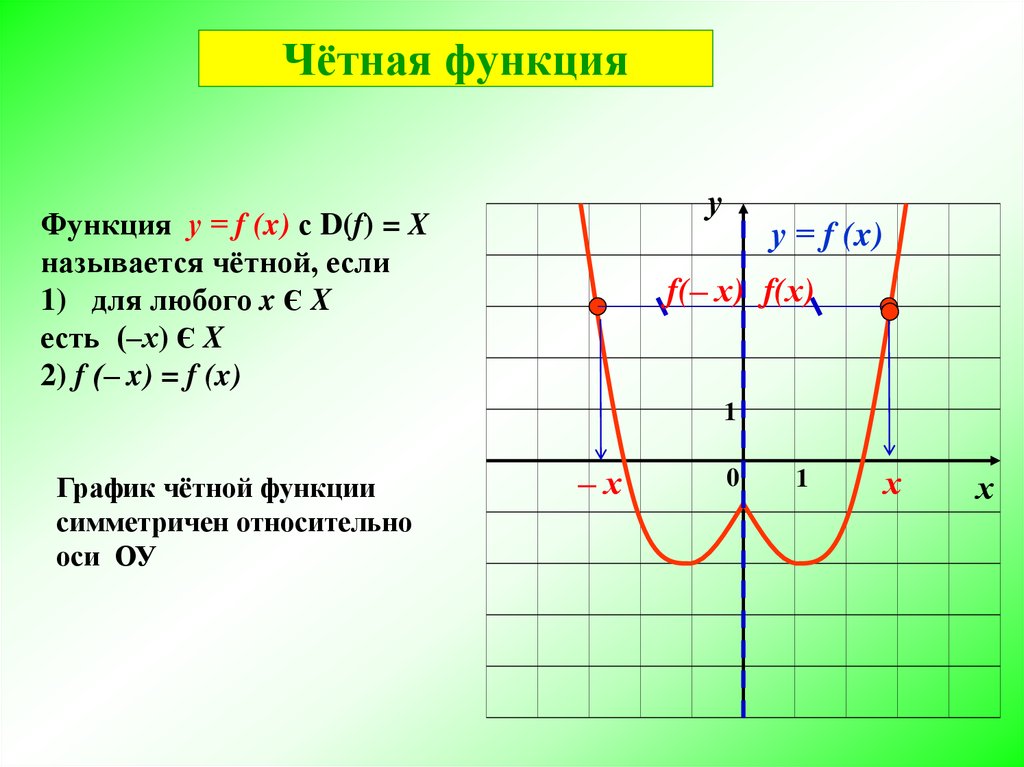
2. Чётная функция
уФункция у = f (x) с D(f) = X
называется чётной, если
1) для любого x Є X
есть (‒х) Є X
2) f (‒ x) = f (x)
у = f (x)
f(‒ х) f(х)
1
График чётной функции
симметричен относительно
оси ОУ
‒х
0
1
х
х
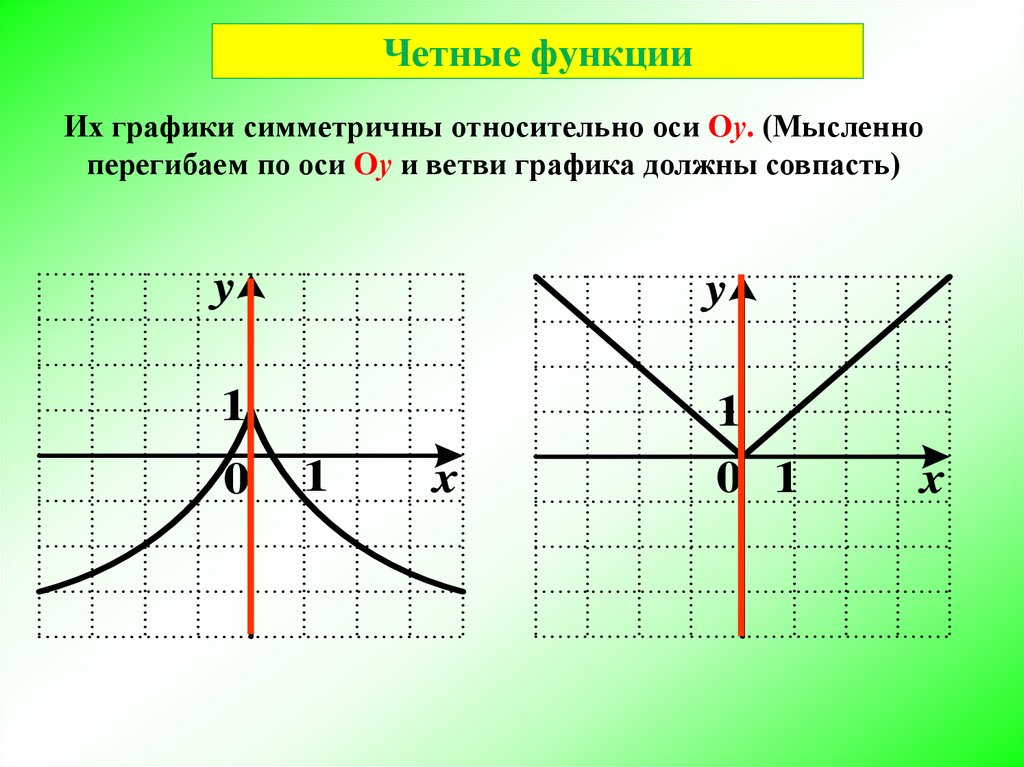
3. Четные функции
Их графики симметричны относительно оси Oу. (Мысленноперегибаем по оси Oу и ветви графика должны совпасть)
y
y
1
1
0 1
0
1
x
x
4.
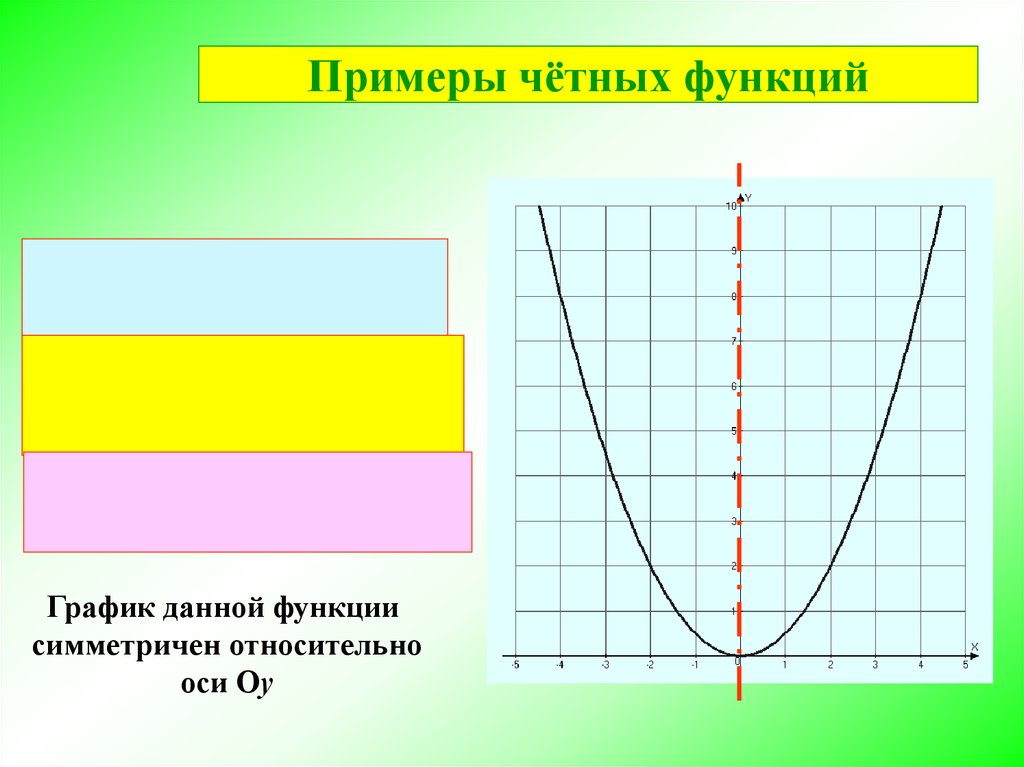
Примеры чётных функций1 2
у ( х) х
2
1
1 2
2
у ( х) ( х) х
2
2
у ( х) у ( х)
График данной функции
симметричен относительно
оси Оу
5.
Примеры чётных функцийу ( х) 0, 25 х 4 3 х 2
у ( х) 0, 25( х) 3( х)
4
0, 25 х 3 х
4
2
2
у ( х) у ( х)
График данной функции
симметричен относительно оси Оу
х
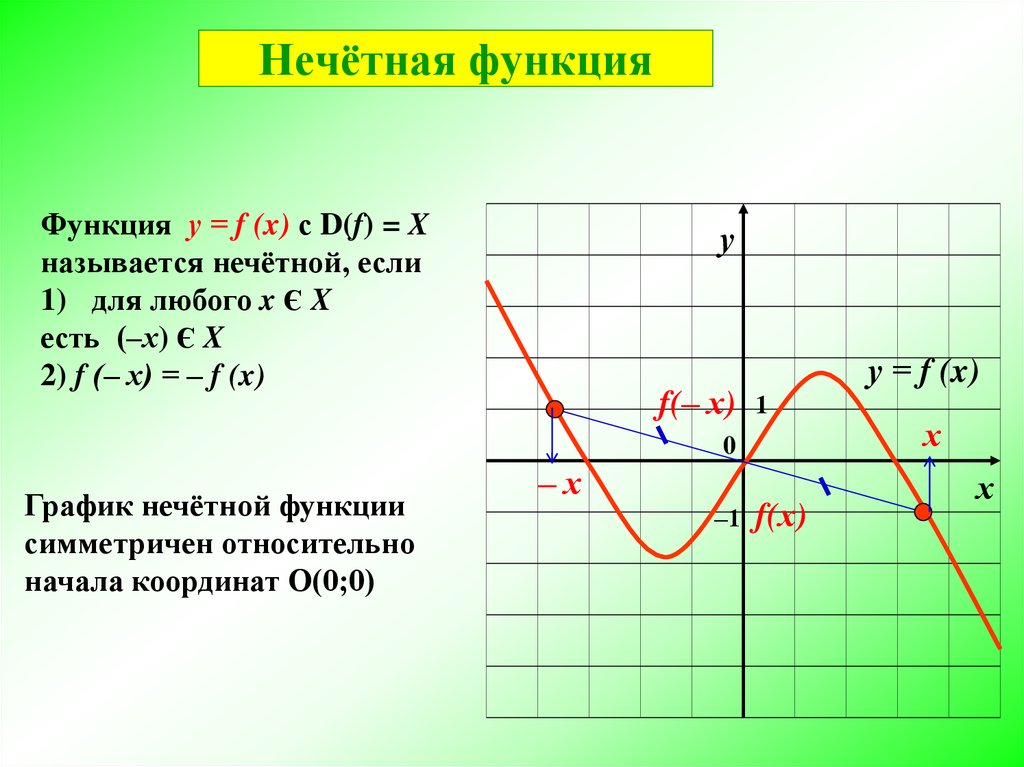
6. Нечётная функция
Функция у = f (x) с D(f) = Xназывается нечётной, если
1) для любого x Є X
есть (‒х) Є X
2) f (‒ x) = ‒ f (x)
у
f(‒ х)
у = f (x)
1
0
График нечётной функции
симметричен относительно
начала координат О(0;0)
‒х
‒1
f(х)
х
х
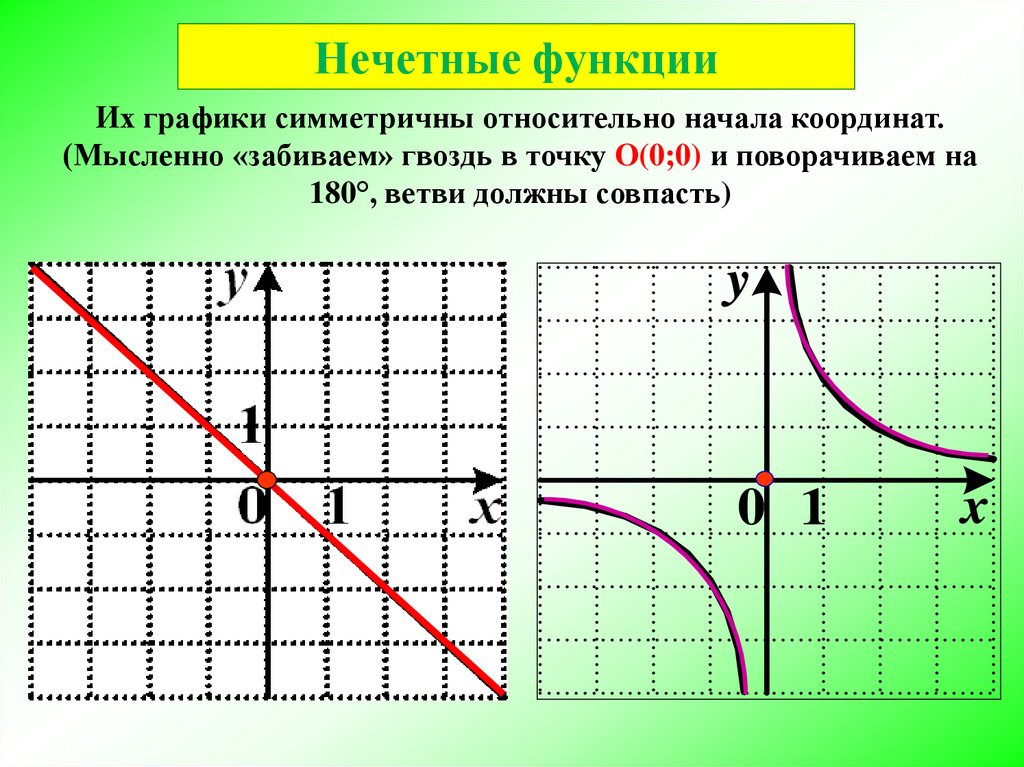
7. Нечетные функции
Их графики симметричны относительно начала координат.(Мысленно «забиваем» гвоздь в точку O(0;0) и поворачиваем на
180°, ветви должны совпасть)
y
0 1
x
8.
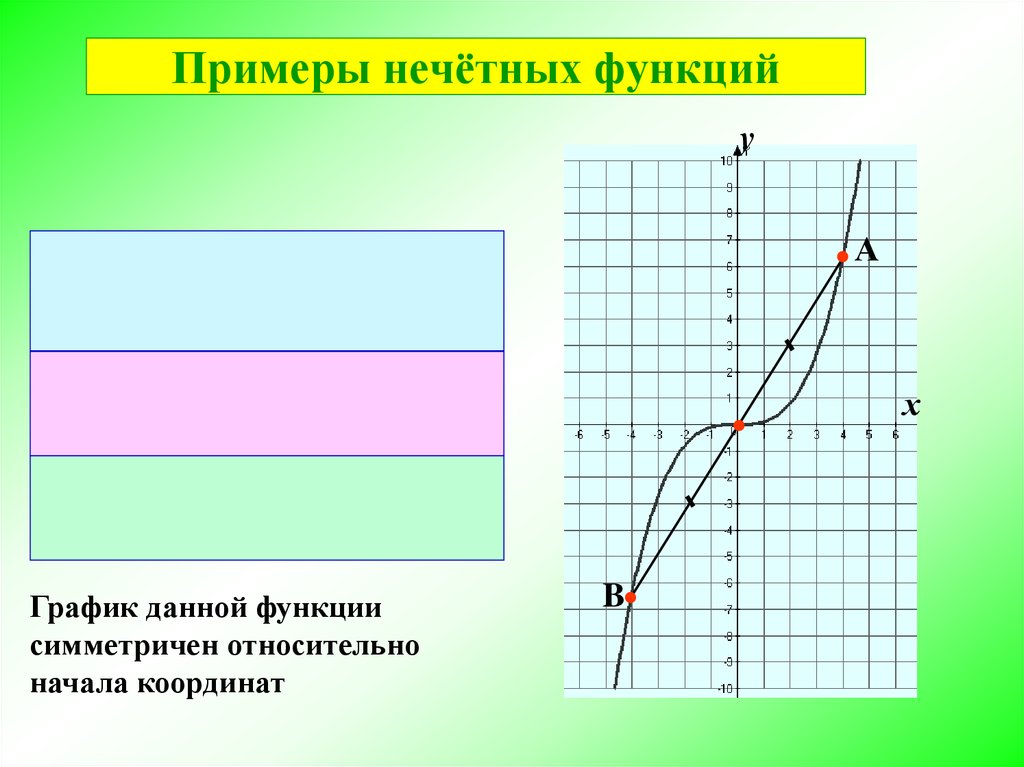
Примеры нечётных функцийу
А
1 3
у ( х) х
10
1
1 3
3
у ( х) ( х) х
10
10
у ( х) у ( х)
График данной функции
симметричен относительно
начала координат
х
B
9.
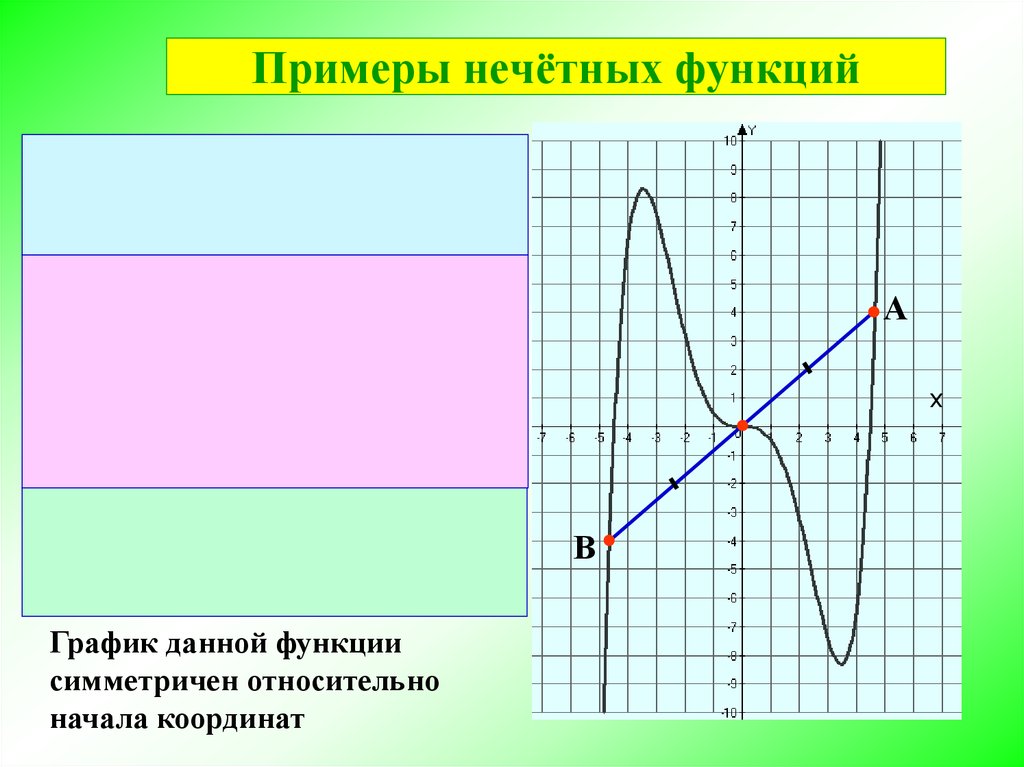
Примеры нечётных функций1 5 1
у ( х)
х х
40
2
А
1
1
5
у ( х) ( х) ( х)
40
2
1 5 1
1 5 1
х х х х
40
2
2
40
у ( х) у ( х)
График данной функции
симметричен относительно
начала координат
х
В
10.
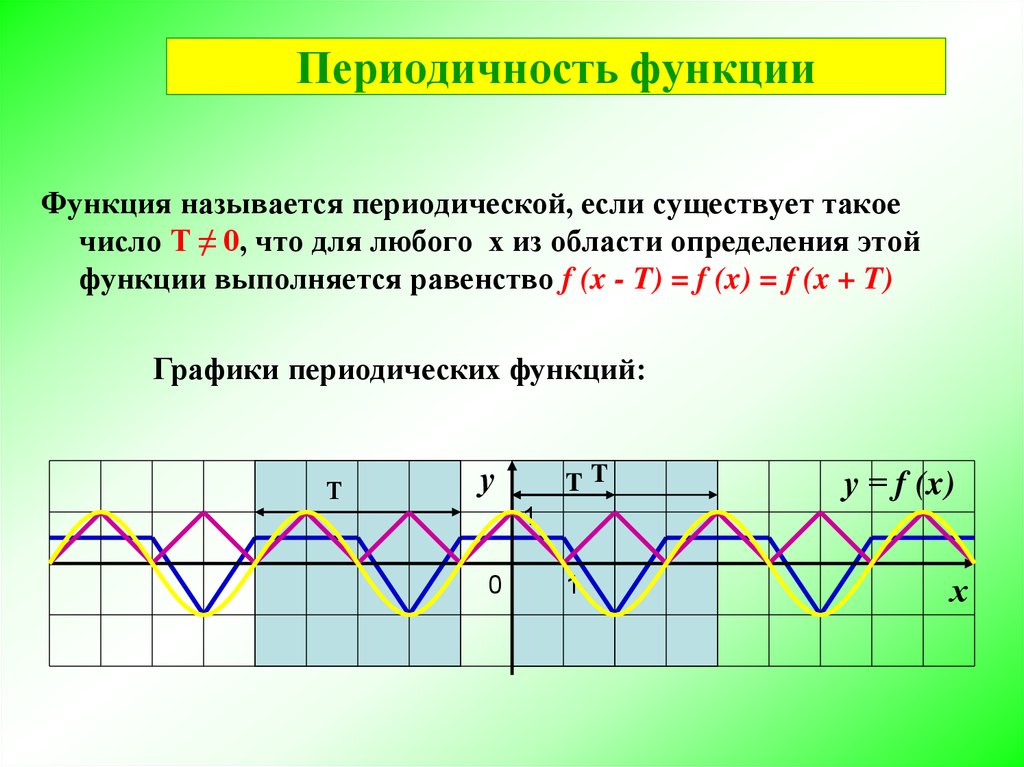
Периодичность функцииФункция называется периодической, если существует такое
число Т ≠ 0, что для любого х из области определения этой
функции выполняется равенство f (x - T) = f (x) = f (x + T)
Графики периодических функций:
Т
у
TT
у = f (x)
1
0
1
х
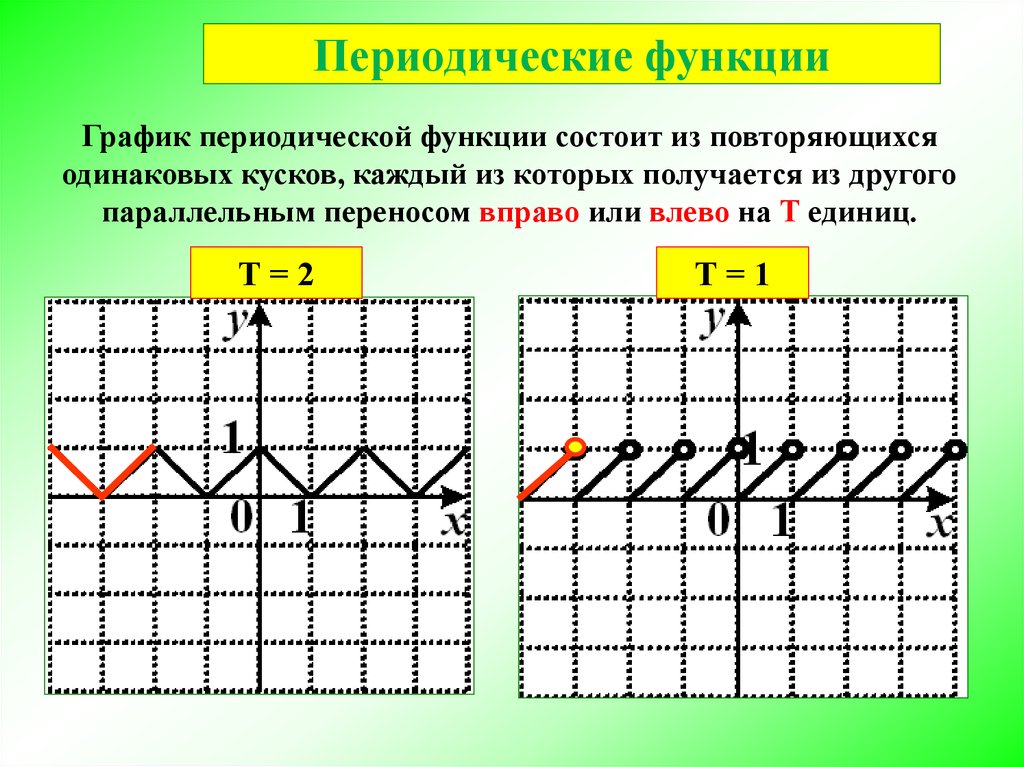
11. Периодические функции
График периодической функции состоит из повторяющихсяодинаковых кусков, каждый из которых получается из другого
параллельным переносом вправо или влево на Т единиц.
Т=2
Т=1
12.
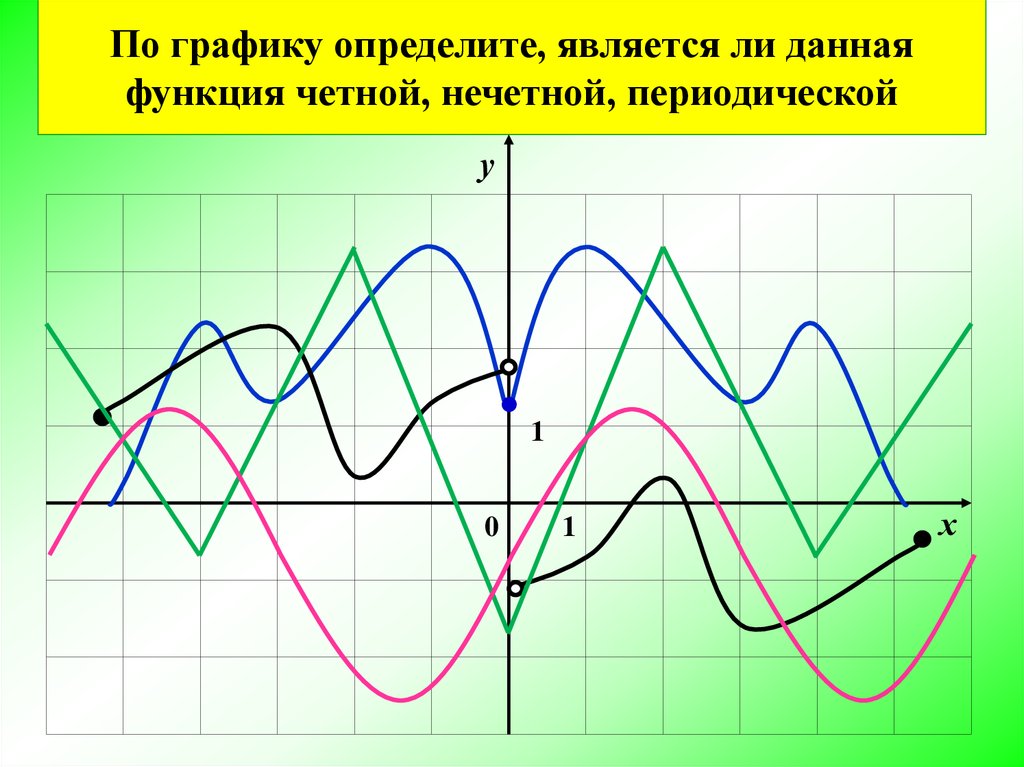
По графику определите, является ли даннаяфункция четной, нечетной, периодической
у
0
1
1
х


 Математика
Математика








