Теоретическая механика. Кинематика. Лекция 2

1.

ТЕОРЕТИЧЕСКА
Я МЕХАНИКА
КИНЕМАТИКА

2. Лекция 2

Ускорение точки – величина,
характеризующая быстроту изменения
скорости точки.
Три способа задания движения точки
определяют способы определения
ускорения точки: векторный,
координатный и естественный

3. Векторный способ

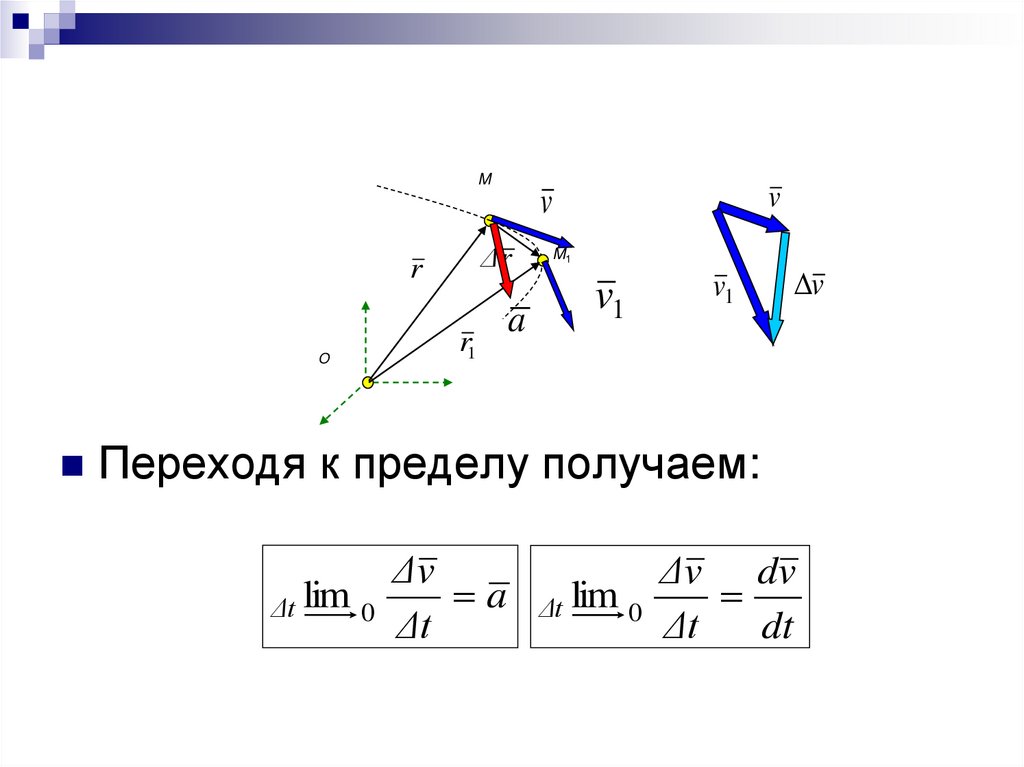
Сравним скорости точки в двух
положениях точки в моменты времени t
и t1= t + t:
t
v;
t1 t Δt v1 v Δv ;
Δv
a ср
Δt
- вектор среднего ускорения
в интервале времени t, направлен в
сторону вогнутости траектории.

4.

M
Δr
r
O
r1
v
v
a
M1
v1
v1
v
Переходя к пределу получаем:
Δv
a
Δt lim 0
Δt
Δ v dv
Δt lim 0
Δt
dt

5.

dv
d 2r
a
dt
dt 2
вектор истинного ускорения
точки в момент времени t, лежит в
соприкасающейся плоскости
(предельное положение плоскости,
проведенной через касательную в точке
M и прямую, параллельную
касательной в точке M1, при
стремлении M1 к M) и направлен в
сторону вогнутости траектории.

6. Координатный способ

Используем полученное векторное
выражение и связь радиуса-вектора с
координатами r (t ) x(t )i y(t ) j z (t )k
z
M
ax
az
ay
r
O
k
z
j
x
i
x
y
y

7.

d 2 r (t ) d 2
a
2 x(t )i y (t ) j z (t )k
2
dt
dt
d 2x
d2y
d 2z
2 i 2 j 2 k axi a y j az k
dt
dt
dt
Компоненты
(составляющие)
вектора ускорения:
Проекции ускорения
на оси координат:
a y y j;
a x x ;
a y y ;
a z z k .
a z z .
a x x i ;
a
x 2 y 2 z 2 ;
x
;
a
y
cos( a , y ) .
a
cos( a , x)

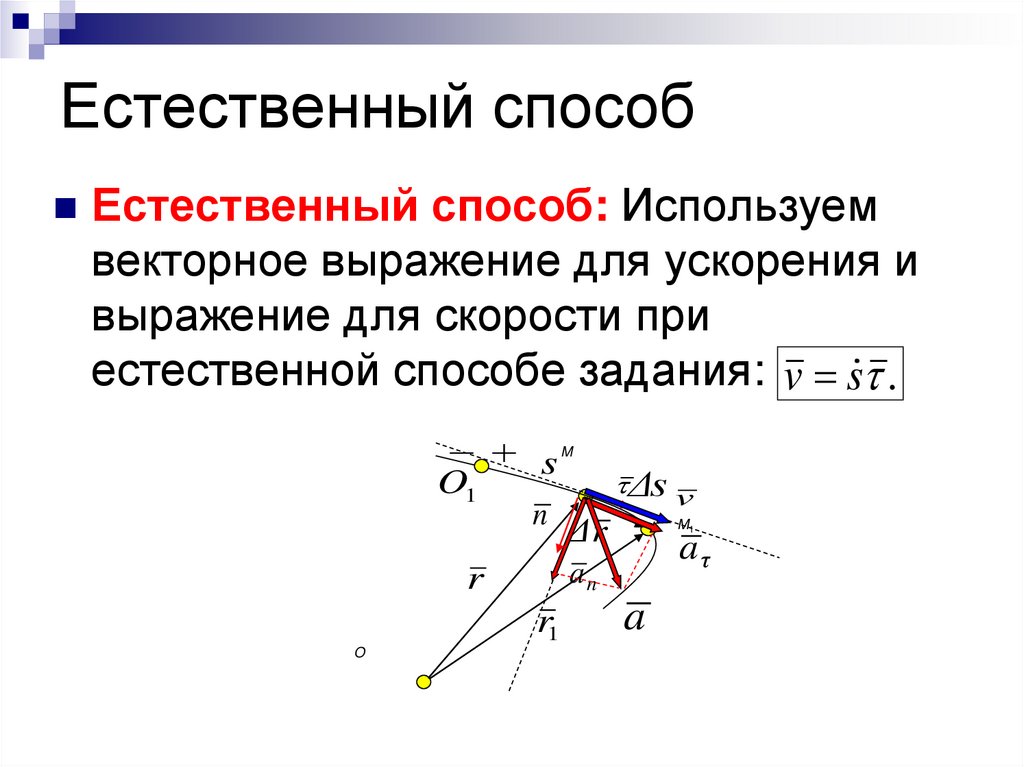
8. Естественный способ

Естественный способ: Используем
векторное выражение для ускорения и
выражение для скорости при
естественной способе задания: v s .
sM
O1
Δs v
n
M
Δr
aτ
an
r
a
r1
1
O

9.

dv d
d
a
( s ) s s
.
dt dt
dt
Представим единичный касательный
вектор как сложную функцию:
(t ) [ s(t )].
Производная единичного касательного
вектора:
d d ds
d
s .
dt
ds dt
ds

10.

Величина производной единичного
касательного вектора по дуговой координате:
2 sin Δ2
d
Δ
1
Δs lim 0
Δ lim 0
.
ds
Δs
Δ
Таким образом, производная единичного
касательного вектора по дуговой координате
есть вектор, направленный перпендикулярно
касательной к траектории.

11.

При s 0 радиус кривизны 1 , угол
между радиусами кривизны 0,
числитель - основание равнобедренного
треугольника, образованного единичными
векторами 1 и , знаменатель – длина
круговой дуги радиуса .
1
Δr
Δ
1
Δs
1

12.

Угол между приращением единичного
вектора и самим вектором при
0, стремится к 90о.
Проекции ускорения на оси
a τ s ;
an
s 2
.
и n:

13.

Таким образом полное ускорение точки
есть векторная сумма двух ускорений:
касательного, направленного по
касательной к траектории в сторону
увеличения дуговой координаты, если s 0
(в противном случае – в противоположную) и
нормального ускорения, направленного по
нормали к касательной в сторону центра
кривизны (вогнутости траектории):
a a τ an .

14.

Введем единичный вектор n,
нормальный (перпендикулярный) к
касательной, направленный к центру
кривизны.
С использованием вектора n и ранее
определенных величин ускорение
представляется как сумма векторов:
a s
s 2
n.

15.

Компоненты (составляющие) вектора
ускорения:
a s ;
s 2
an n.
Модуль полного ускорения:
a a τ an ;
2
2

16.

Равнопеременное движение точки –
движение точки по траектории, при
котором касательное ускорение не
изменяется по величине.
a τ s const.
Запишем выражение для касательного
ускорения через проекцию скорости:
dv τ
d
a τ s s
dt
dt

17.

Полученное выражение есть
дифференциальное уравнение, которое
легко решается разделением
переменных и интегрированием левой и
правой частей: dv τ a τ dt
vτ
t
dv τ a τ τ dt;
vτ 0
0
vτ
vτ v
τ0
t
aτ τ t 0 ;
v τ v τ 0 a τ τt
v τ v τ 0 a τ τt - скорость точки при
равнопеременном движении

18.

В свою очередь скорость точки также
связывается с дуговой координатой
дифференциальной зависимостью:
vτ
ds
или ds vτ dt.
dt
После подстановки выражения для скорости
и интегрирования получаем:
s
t
ds (v a t )dt;
τ0
s0
0
t2
s s0 vτ 0t aττ
2
t
t
t2
s s (vτ 0t a ) ; s s0 vτ 0t a .
0
2 0
2
s
2
дуговая координата точки при
равно-переменном движении

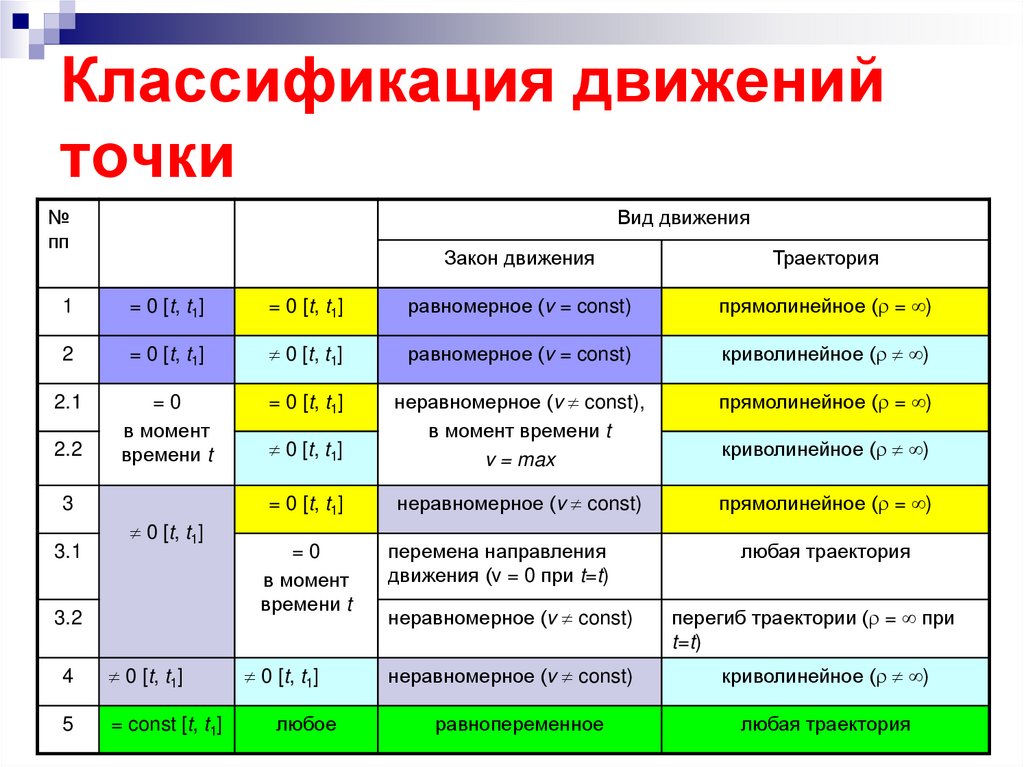
19. Классификация движений точки

№
пп
Вид движения
Закон движения
Траектория
1
= 0 [t, t1]
= 0 [t, t1]
равномерное (v = const)
прямолинейное ( = )
2
= 0 [t, t1]
0 [t, t1]
равномерное (v = const)
криволинейное ( )
2.1
=0
в момент
времени t
= 0 [t, t1]
прямолинейное ( = )
0 [t, t1]
неравномерное (v const),
в момент времени t
v = max
= 0 [t, t1]
неравномерное (v const)
прямолинейное ( = )
=0
в момент
времени t
перемена направления
движения (v = 0 при t=t)
любая траектория
неравномерное (v const)
перегиб траектории ( = при
t=t)
неравномерное (v const)
криволинейное ( )
равнопеременное
любая траектория
2.2
3
3.1
0 [t, t1]
3.2
4
0 [t, t1]
5
= const [t, t1]
0 [t, t1]
любое
криволинейное ( )

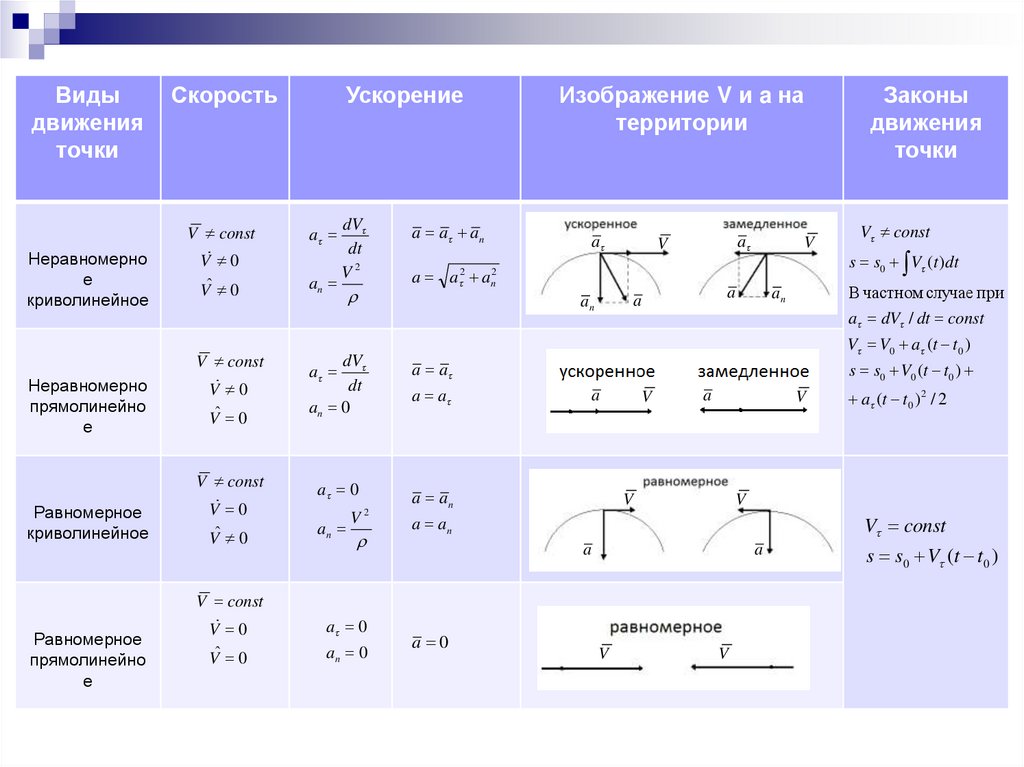
20.

Виды
движения
точки
Неравномерно
е
криволинейное
Неравномерно
прямолинейно
е
Равномерное
криволинейное
Равномерное
прямолинейно
е
Скорость
Ускорение
dV
dt
V2
a a an
V const
V 0
a
Vˆ 0
an
V const
V 0
dV
a
dt
an 0
a a
a 0
a an
Vˆ 0
V const
V 0
Vˆ 0
an
V2
V const
V 0
a 0
Vˆ 0
an 0
Изображение V и a на
территории
a
a
V
a a 2 an2
a
a
an
V
Законы
движения
точки
V const
s s0 V (t )dt
В частном случае при
a dV / dt const
an
V V0 a (t t0 )
s s0 V0 (t t0 )
a a
a
V
a
V
V
V
V const
a an
a
a 0
a (t t0 ) 2 / 2
a
V
V
s s0 V (t t0 )

21.

Кинематика твердого тела – изучает
движение твердого тела, кинематика точки
используется для получения новых
зависимостей и формул.
Исследование работы кривошипношатунного механизма – См. решение
задачи М.12.18 “Теоретическая механика в
примерах и задачах. Кинематика”
(электронное пособие
www.miit.ru/institut/ipss/faculties/trm/main.htm )

22.

Существует пять видов движения твердого тела:
1. Поступательное (ползун, поршень насоса, спарник
колес паровоза, движущегося по прямолинейному
пути, кабина лифта, дверь купе, кабина колеса
обозрения).
2. Вращательное (маховик, кривошип, коромысло,
колесо обозрения, обычная дверь).
3. Плоскопараллельное или плоское (шатун, колесо
локомотива при качении по прямолинейному рельсу,
шлифовальный круг)
4. Сферическое (гироскоп, шаровая стойка)
5. Общий случай движения или свободный полет
(пуля, камень, небесное тело)

23.

Поступательное движение твердого тела –
такое движение при котором любая прямая,
жестко связанная с телом, остается
параллельной самой себе.
Обычно поступательное движение
отождествляется с прямолинейным
движением его точек, однако это не так.
Точки и само тело (центр масс тела) могут
двигаться по криволинейным траекториям,
см. например, движение кабины колеса
обозрения.

24. Поступательное движение

Теорема о поступательном движении
твердого тела – При поступательном
движении твердого тела все его
точки описывают тождественные
траектории и имеют в каждый
момент времени геометрически
равные скорости и ускорения.

25.

vA
A
aA
rBA
rA
rBA
rA
vB
B
rB
C
rB
aB
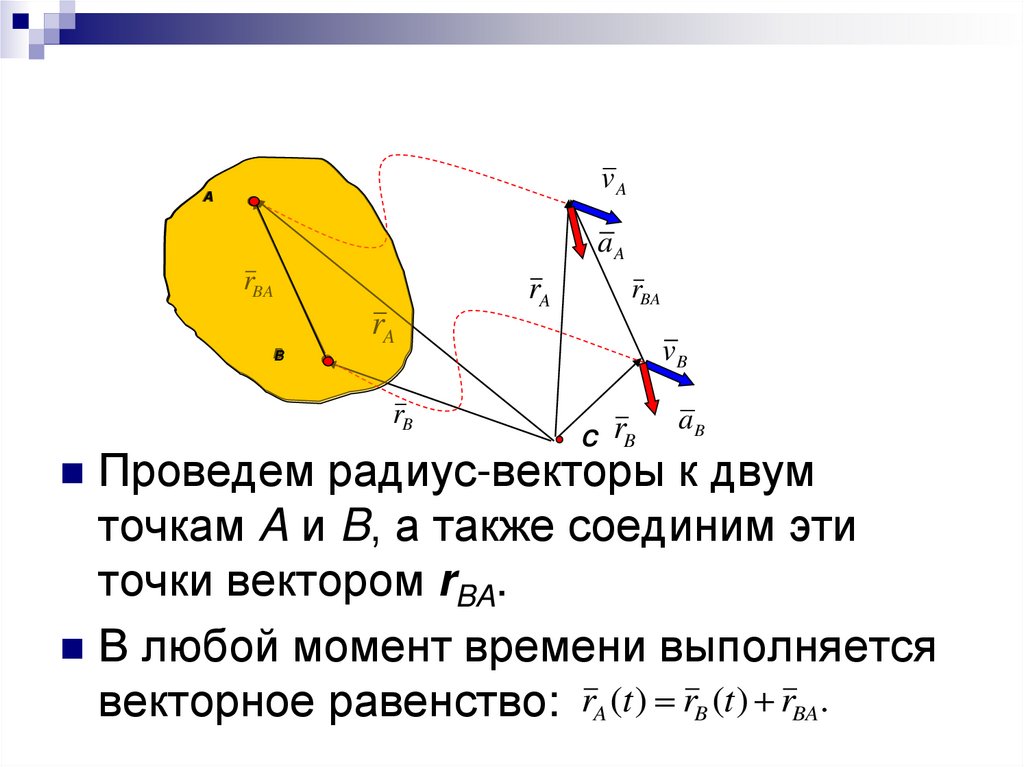
Проведем радиус-векторы к двум
точкам A и B, а также соединим эти
точки вектором rBA.
В любой момент времени выполняется
векторное равенство: rA (t ) rB (t ) rBA.

26.

В любой момент времени вектор rBA
остается постоянным по направлению
(по определению поступательного движения)
и по величине (расстояние между точками
не изменяется).
Отсюда: rA (t ) rB (t ) const , и это означает, что в
каждый момент времени положение точки A
отличается от положения точки B на одну и
ту же величину rBA = const, т.е. траектории
этих двух точек тождественны (совпадают
друг с другом при наложении).

27.

Продифференцируем по времени
левую и правую часть соотношения:
drA (t ) drB (t )
dt
dt
Это означает, что в каждый момент
времени скорость точки A равна
геометрически (т.е. векторно)
скорости точки B.
vA (t ) vB (t ).

28.

Второе дифференцирование по
времени приводит к соотношению:
dr 2 A (t ) dr 2 B (t )
2
2
dt
dt
Это означает,
что в каждый момент
времени ускорение точки A равно
геометрически (т.е. векторно)
ускорению точки B.
aA (t ) aB (t ).

29.

Таким образом, поступательное
движение твердого тела полностью
определяется движением одной
точки, принадлежащей этому телу и
выбранной произвольным образом.
Все параметры движения этой точки
(траектория, скорость и ускорение)
описываются уравнениями и
соотношениями кинематики точки.

30. Спасибо за внимание!