Отображение плоскости на себя. Осевая симметрия. Центральная симметрия

1.

Отображение плоскости на себя.
Осевая симметрия.
Центральная симметрия.

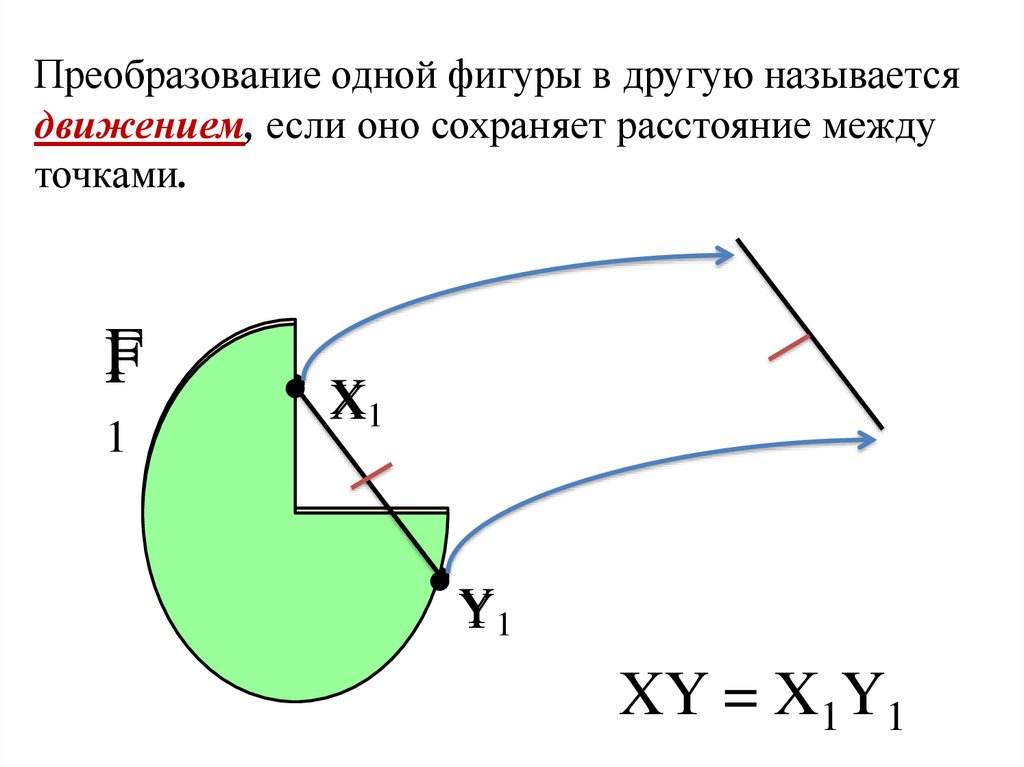
2. Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками.

F
1
X1
Y1
XY = X1Y1

3.

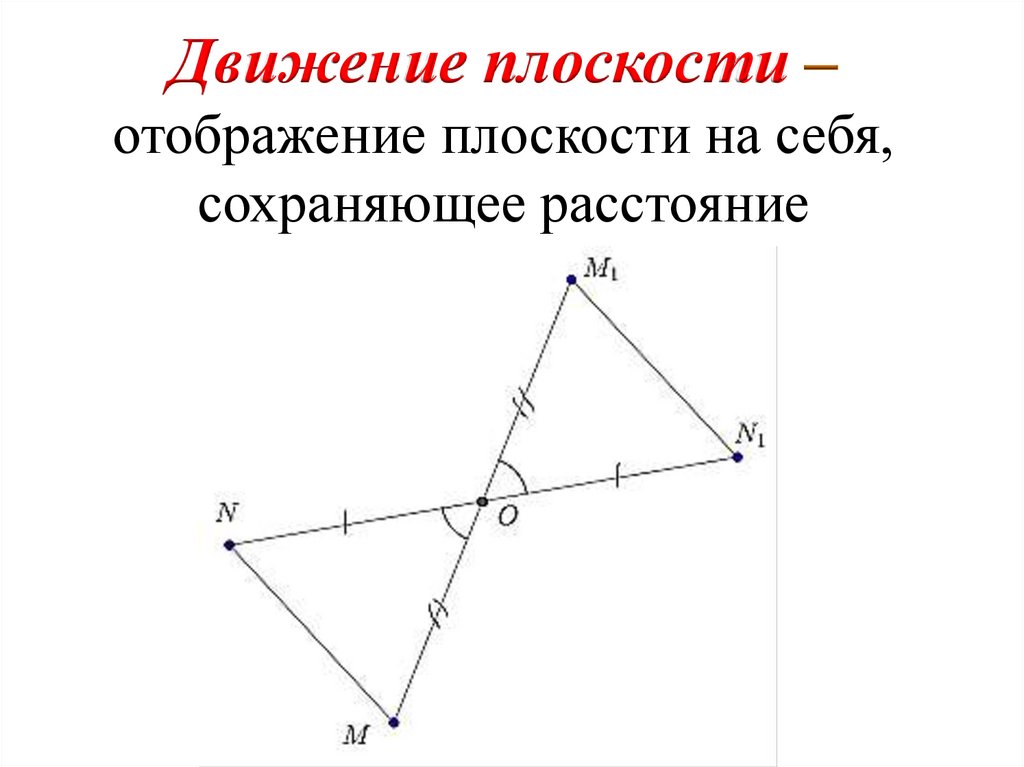
Движение плоскости
отображение плоскости на себя,
сохраняющее расстояние

4.

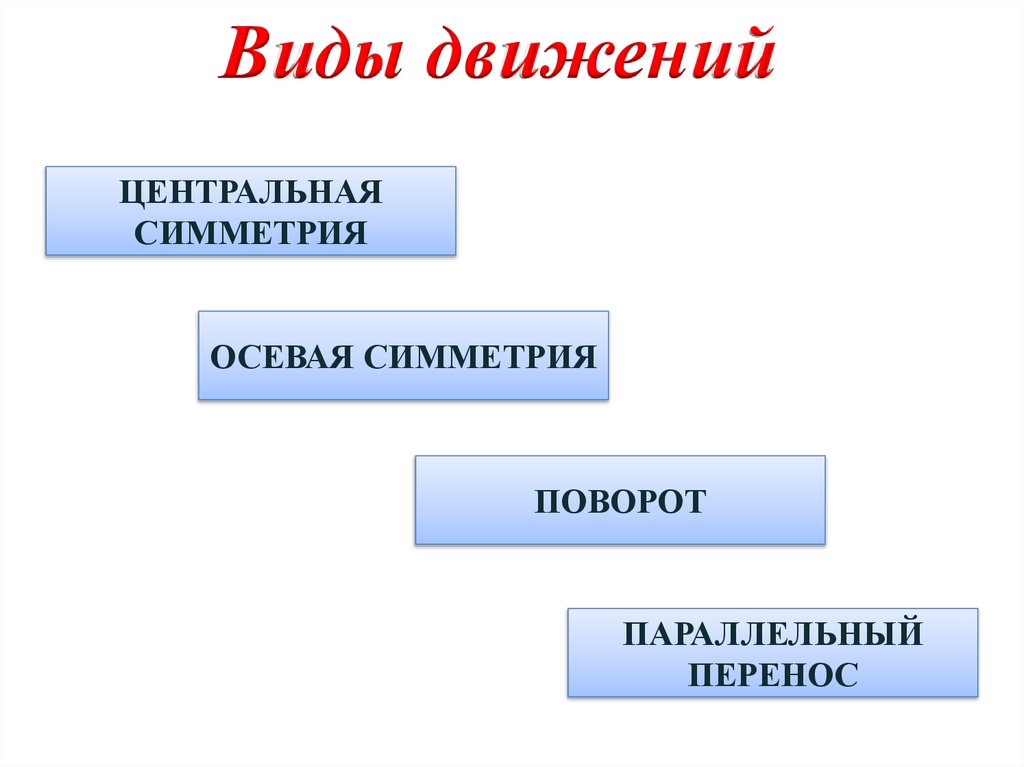
Виды движений
ЦЕНТРАЛЬНАЯ
СИММЕТРИЯ
ОСЕВАЯ СИММЕТРИЯ
ПОВОРОТ
ПАРАЛЛЕЛЬНЫЙ
ПЕРЕНОС

5.

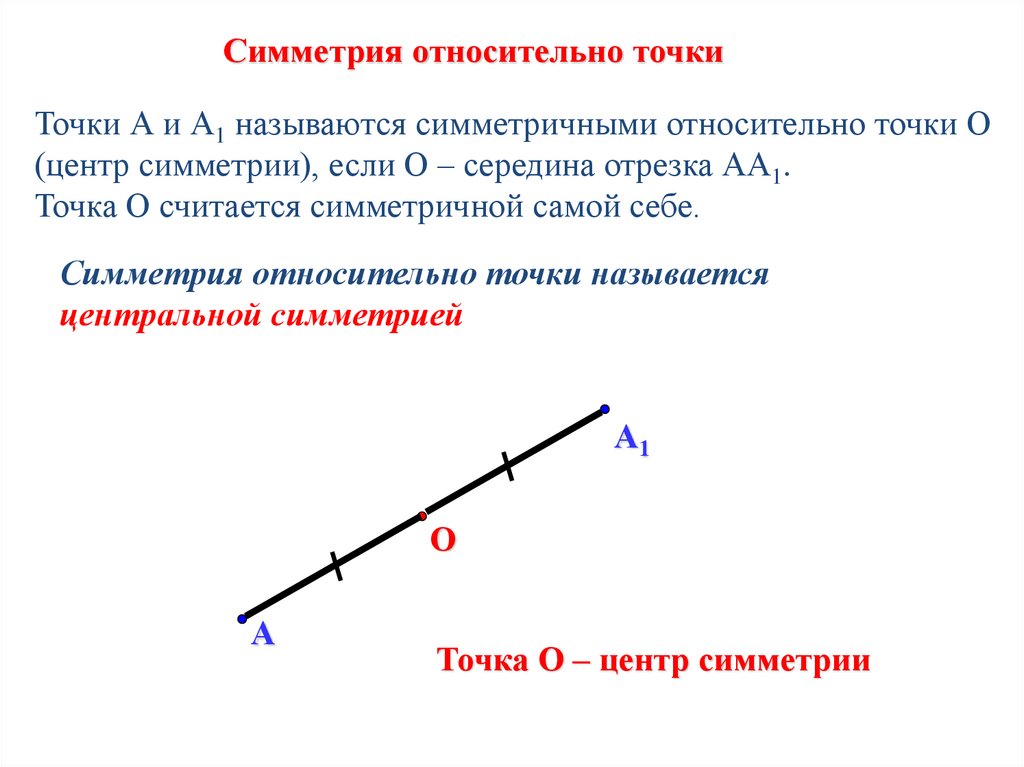
Симметрия относительно точки
Точки А и А1 называются симметричными относительно точки О
(центр симметрии), если О – середина отрезка АА1.
Точка О считается симметричной самой себе.
Симметрия относительно точки называется
центральной симметрией
А1
О
А
Точка О – центр симметрии

6.

Построить отрезок А1В1 симметричный отрезку АВ
относительно точки О
Точка О –
центр симметрии
А
1
В
О
А
В1
А А1 , В В1 , АВ А1В1
Замечание:
при симметрии относительно центра изменился порядок точек (верх-низ,
право-лево).
Например, точка А отобразилась снизу вверх; она была правее точки В, а ее
образ точка А1 оказалась левее точки В1.

7.

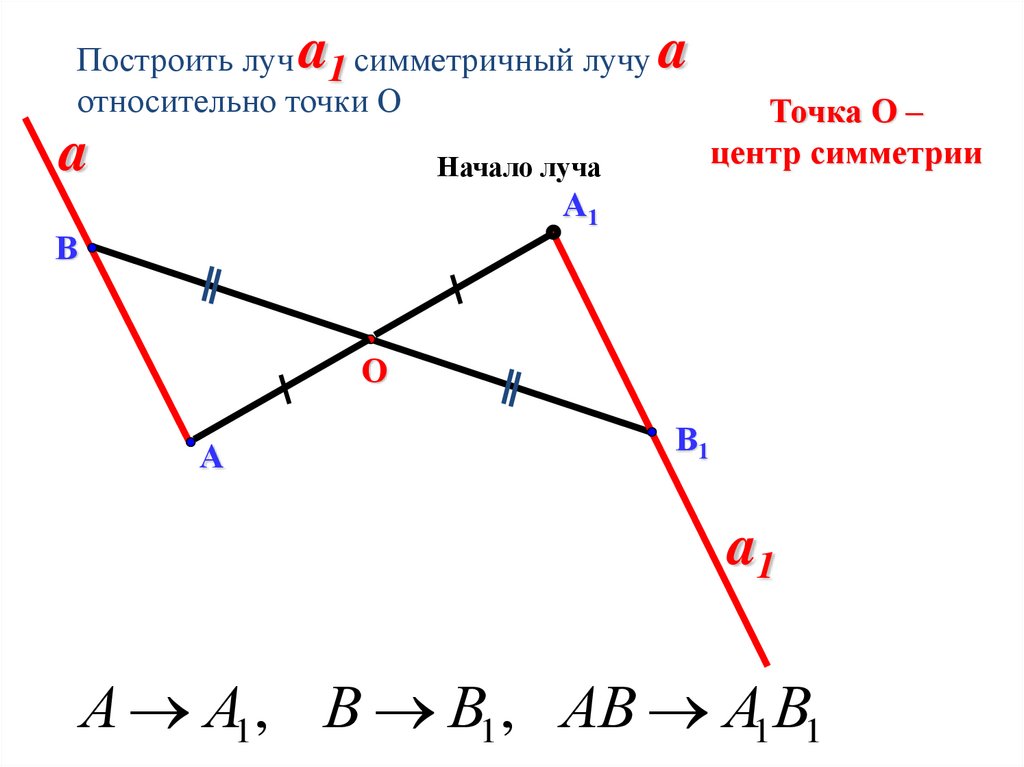
a
Построить луч 1 симметричный лучу
относительно точки О
a
a
Точка О –
центр симметрии
Начало луча
А1
В
О
А
В1
a1
А А1 , В В1 , АВ А1В1

8.

b
a
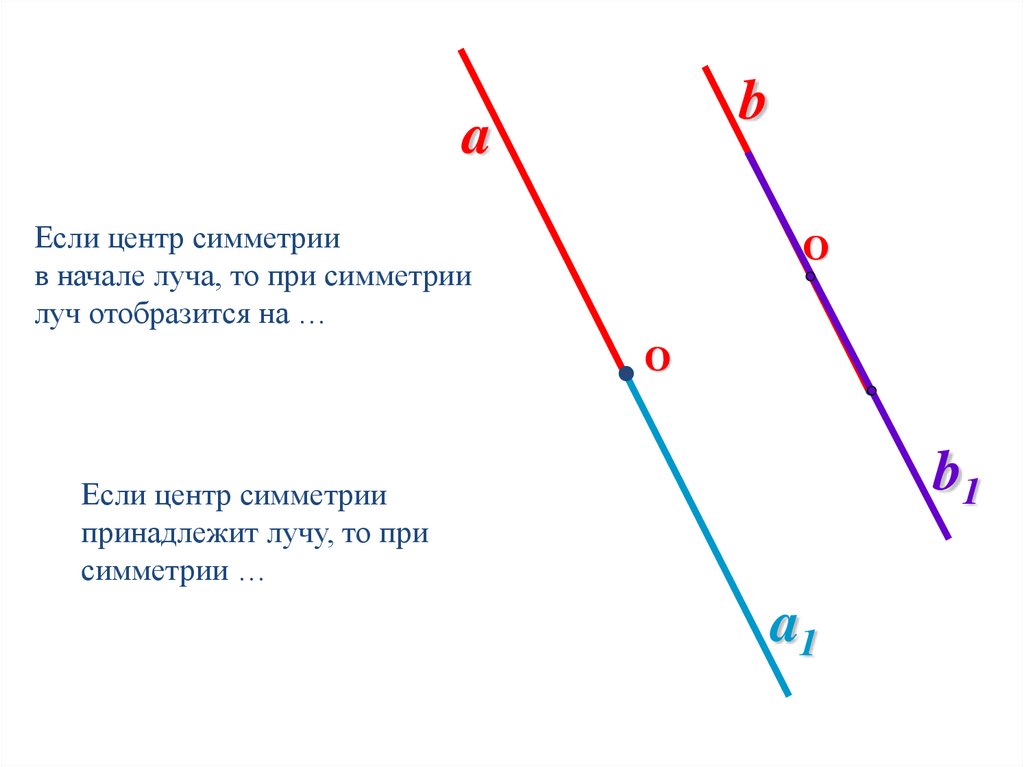
Если центр симметрии
в начале луча, то при симметрии
луч отобразится на …
О
О
b1
Если центр симметрии
принадлежит лучу, то при
симметрии …
a1

9.

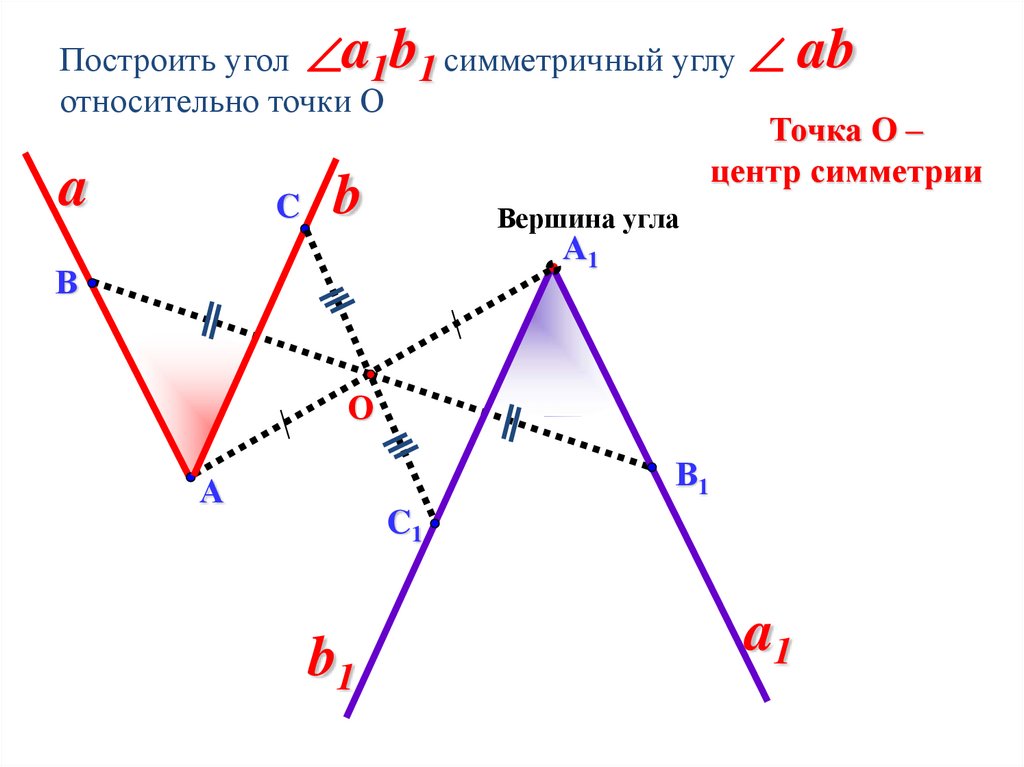
Построить угол 1 1 симметричный углу
относительно точки О
Точка О –
центр симметрии
C
Вершина угла
А1
В
ab
a
ab
b
О
В1
А
C1
b1
a1

10.

b
a
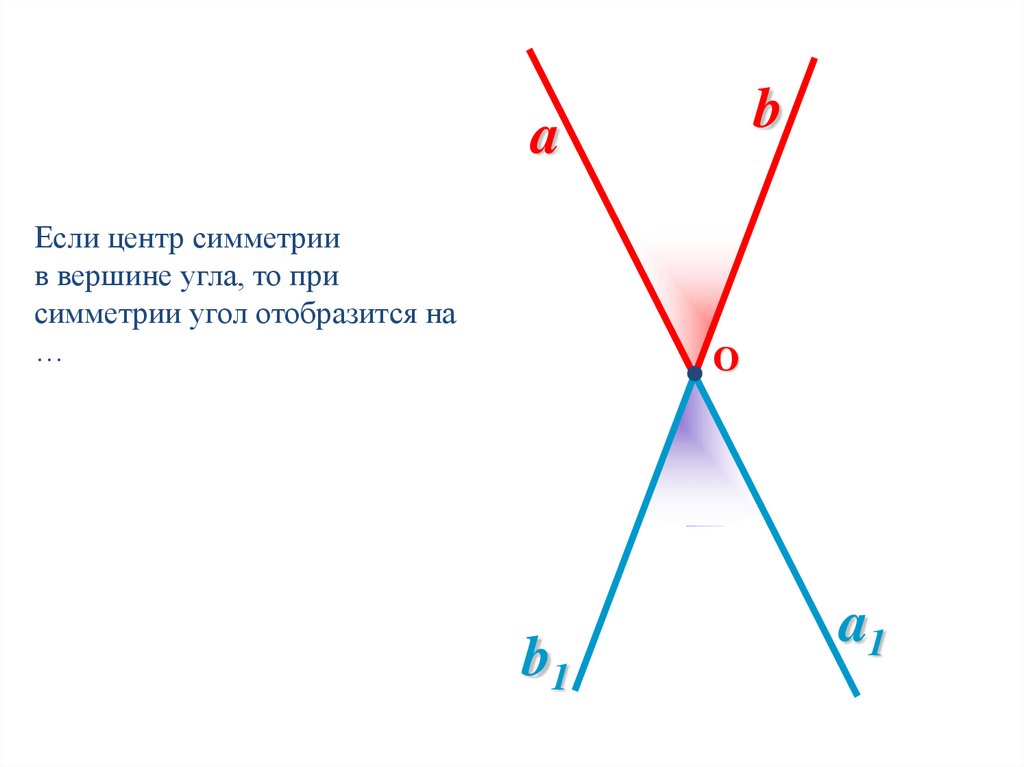
Если центр симметрии
в вершине угла, то при
симметрии угол отобразится на
…
О
b1
a1

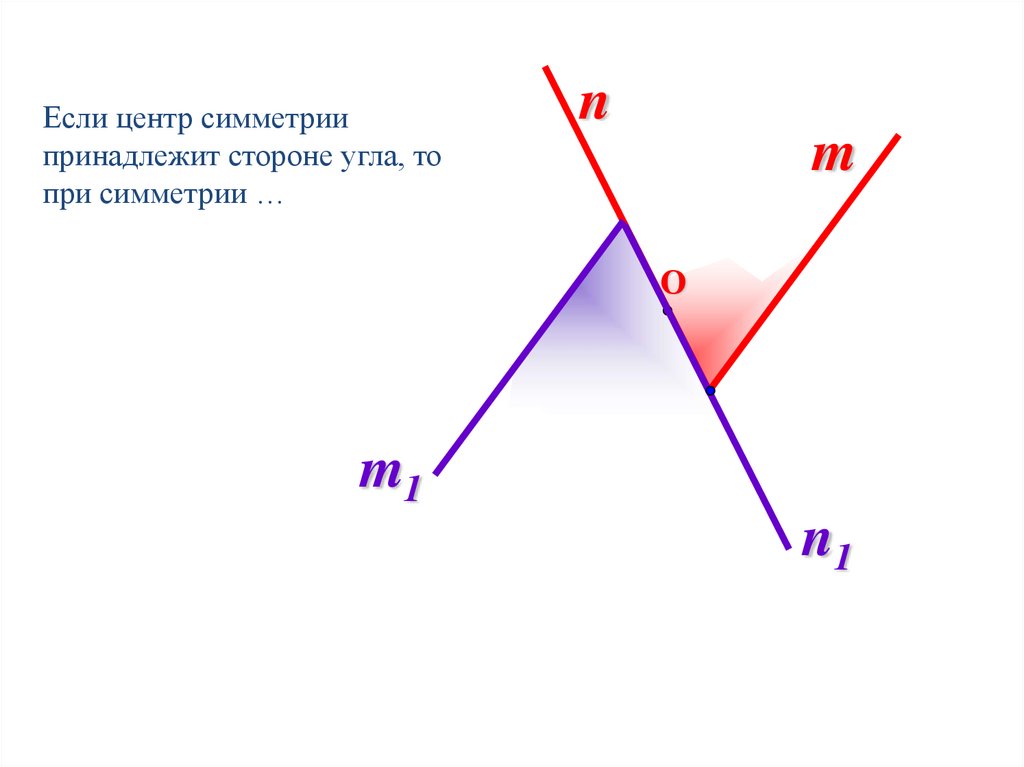
11.

Если центр симметрии
принадлежит стороне угла, то
при симметрии …
n
m
О
m1
n1

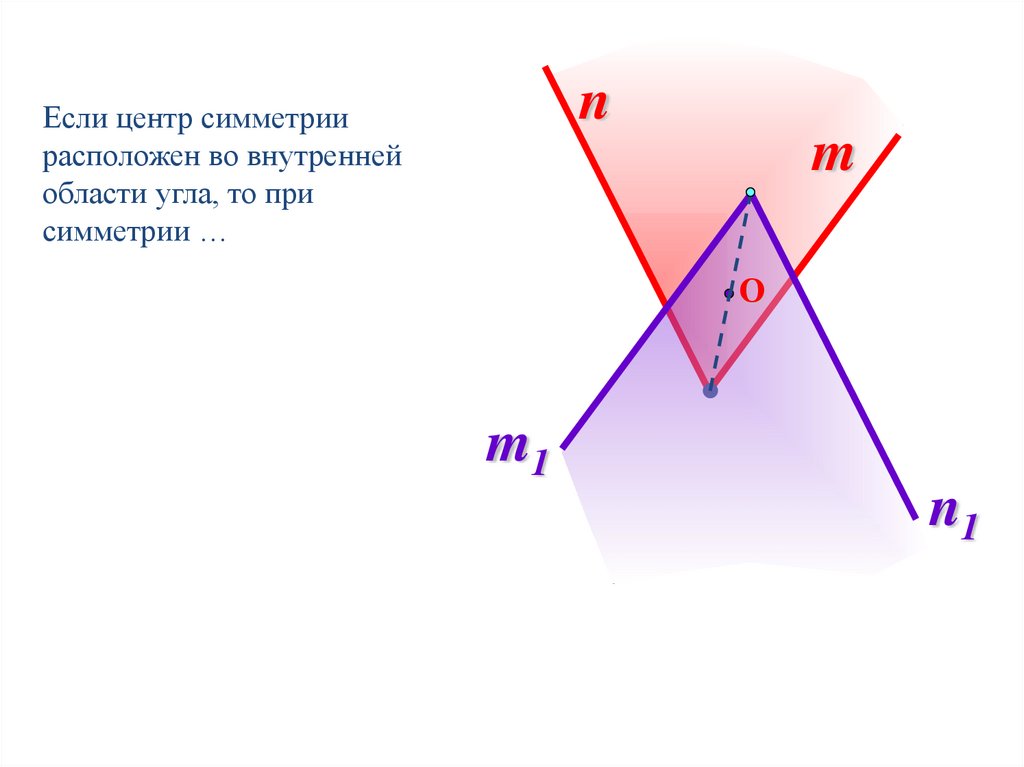
12.

n
Если центр симметрии
расположен во внутренней
области угла, то при
симметрии …
m
О
m1
n1

13.

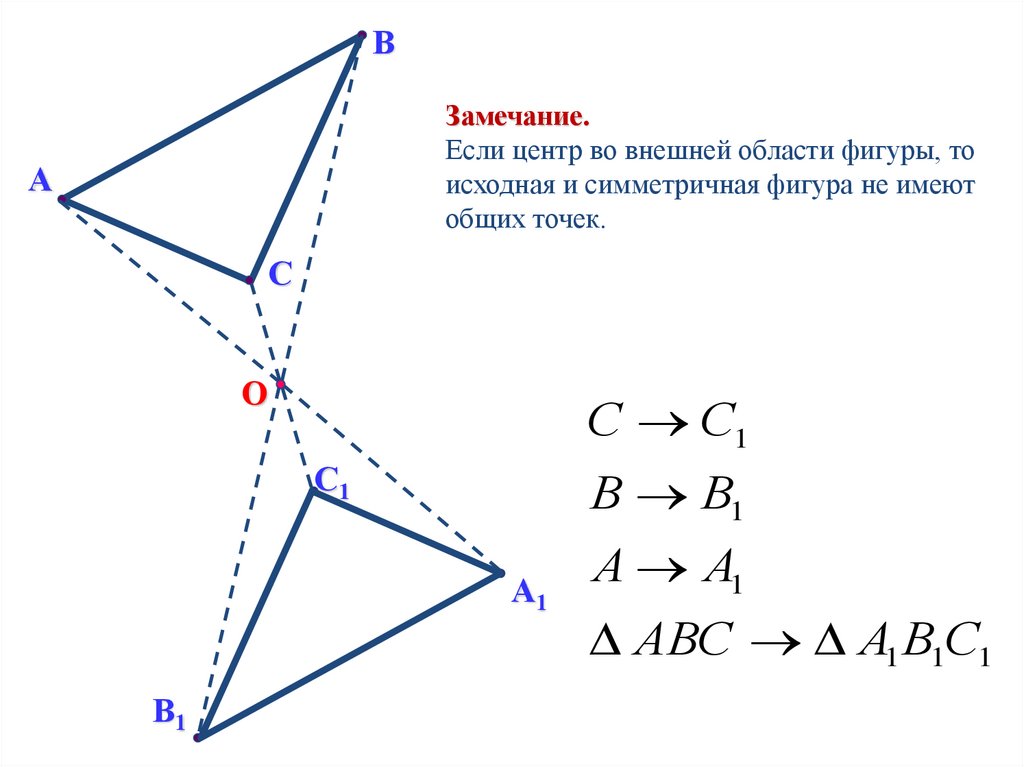
В
Замечание.
Если центр во внешней области фигуры, то
исходная и симметричная фигура не имеют
общих точек.
А
С
О
С С1
С1
В В1
А1
В1
А А1
АВС А1 В1С1

14.

В
С1
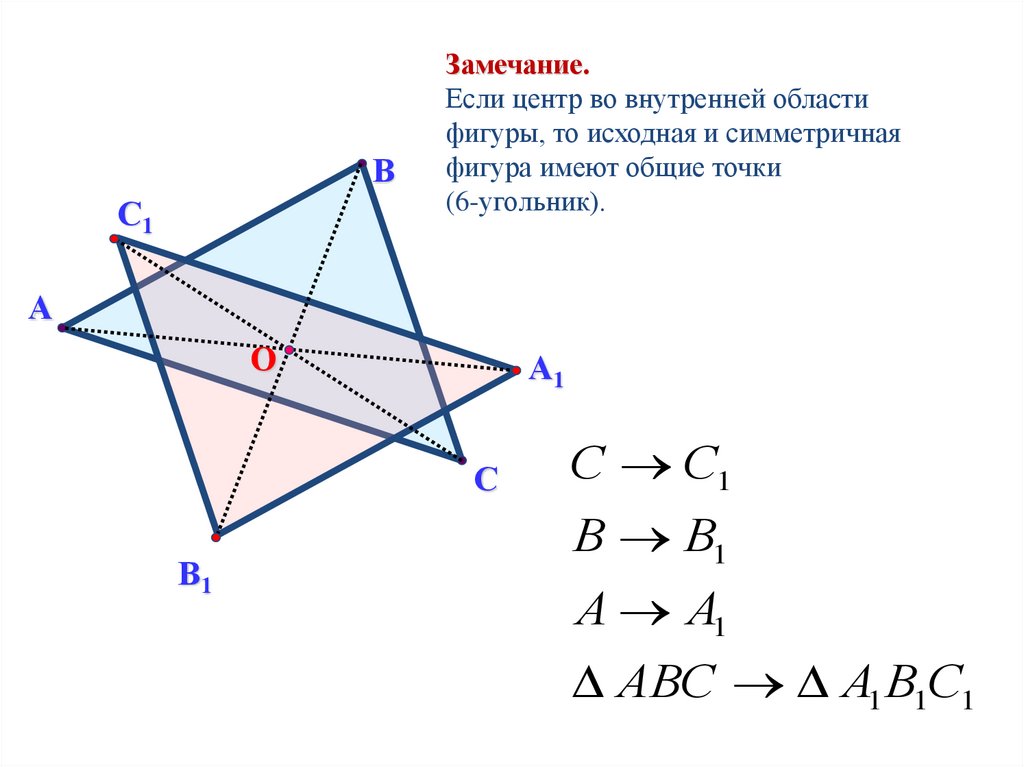
Замечание.
Если центр во внутренней области
фигуры, то исходная и симметричная
фигура имеют общие точки
(6-угольник).
А
О
А1
С
В1
С С1
В В1
А А1
АВС А1 В1С1

15.

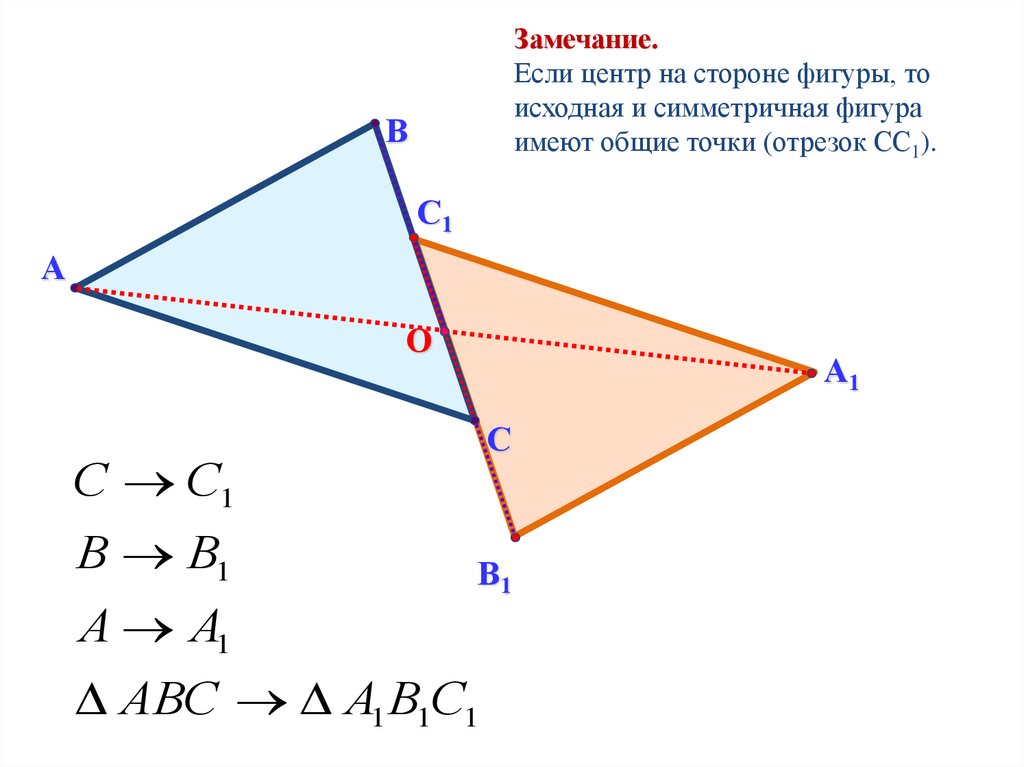
Замечание.
Если центр на стороне фигуры, то
исходная и симметричная фигура
имеют общие точки (отрезок СС1).
В
С1
А
О
А1
С
С С1
В В1
А А1
В1
АВС А1 В1С1

16.

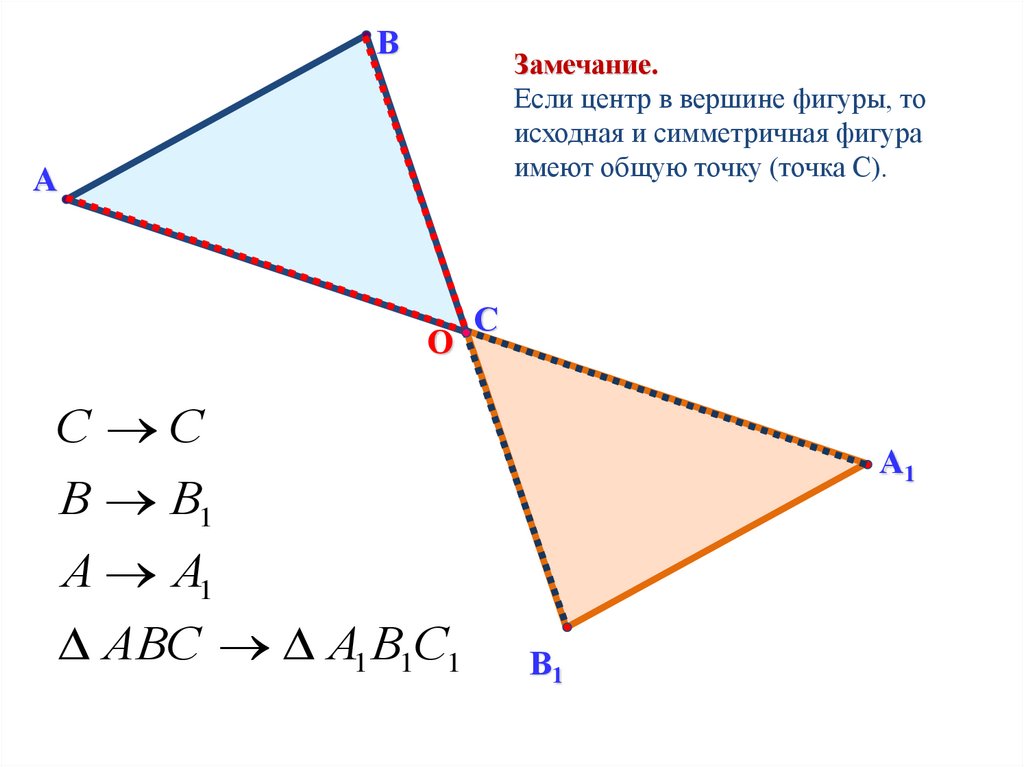
В
Замечание.
Если центр в вершине фигуры, то
исходная и симметричная фигура
имеют общую точку (точка С).
А
О
С
С С
В В1
А1
А А1
АВС А1 В1С1
В1

17.

18.

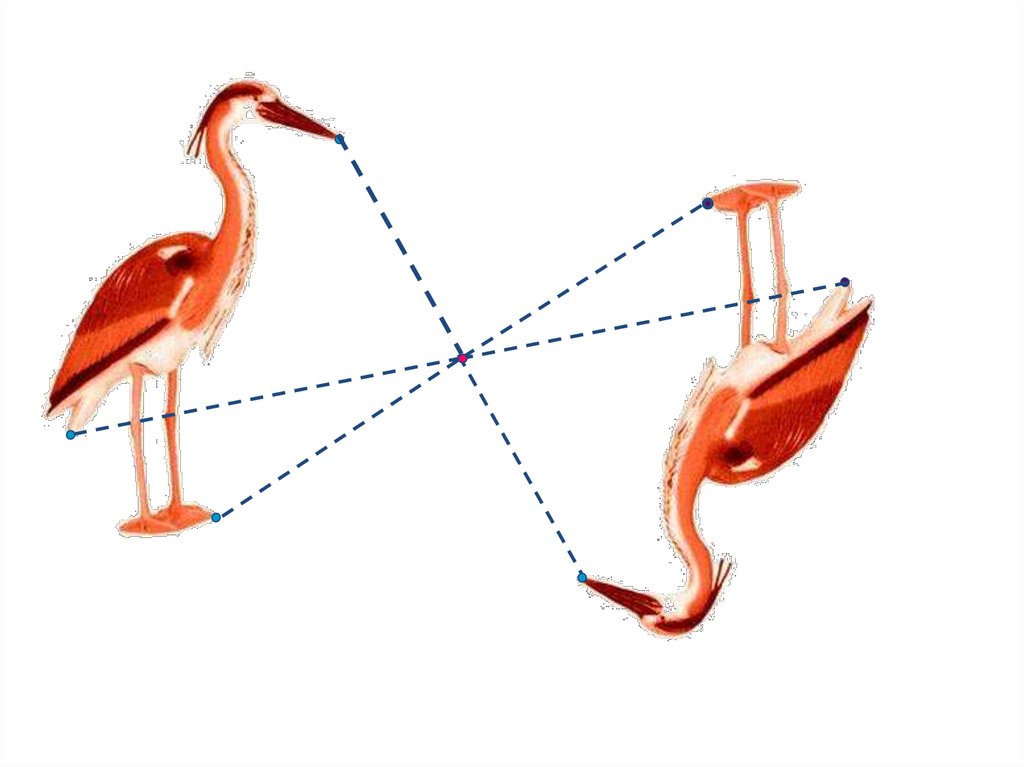
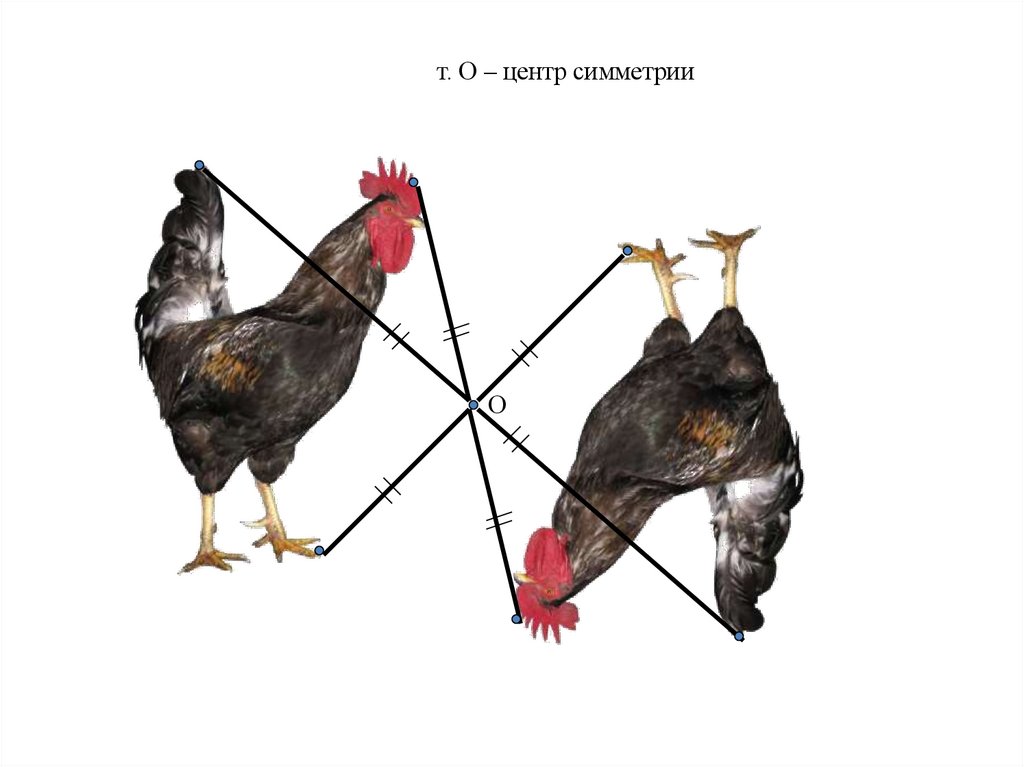
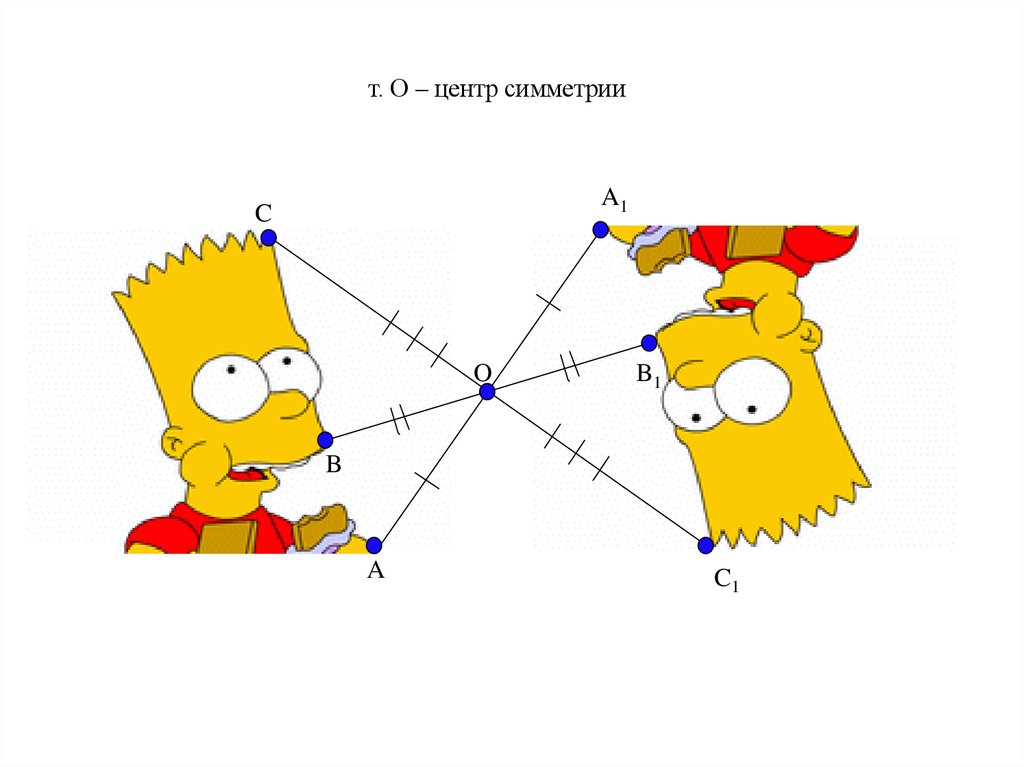
т. О – центр симметрии
О

19.

т. О – центр симметрии
A1
C
O
B1
B
A
C1

20.

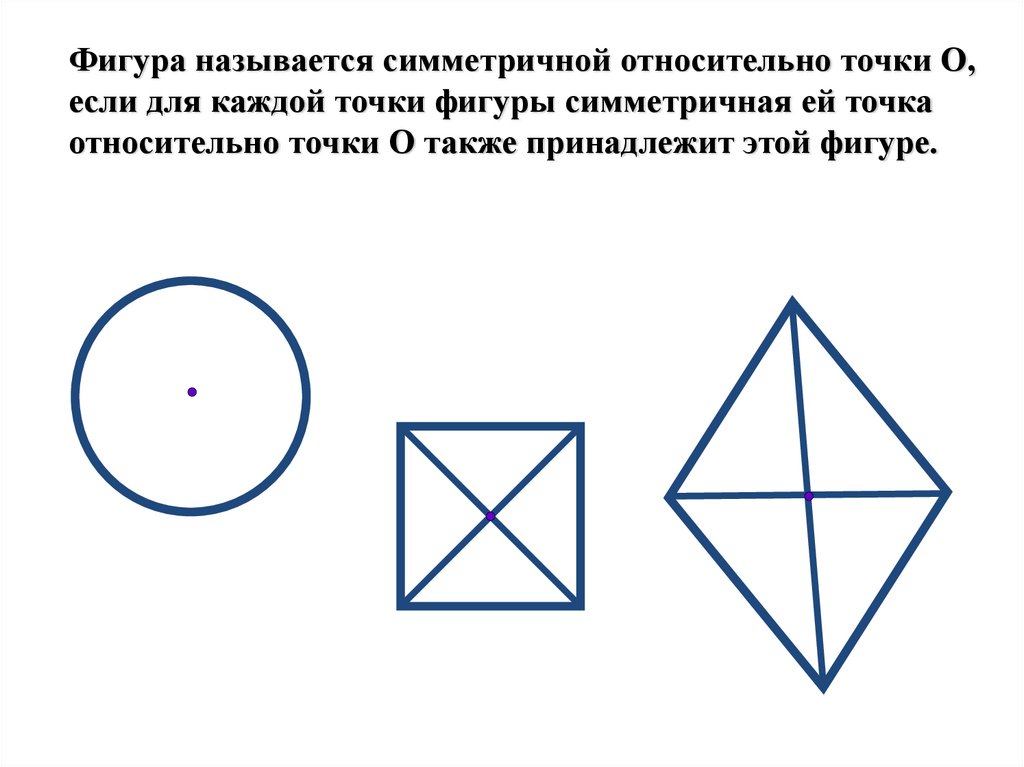
Фигура называется симметричной относительно точки О,
если для каждой точки фигуры симметричная ей точка
относительно точки О также принадлежит этой фигуре.

21.

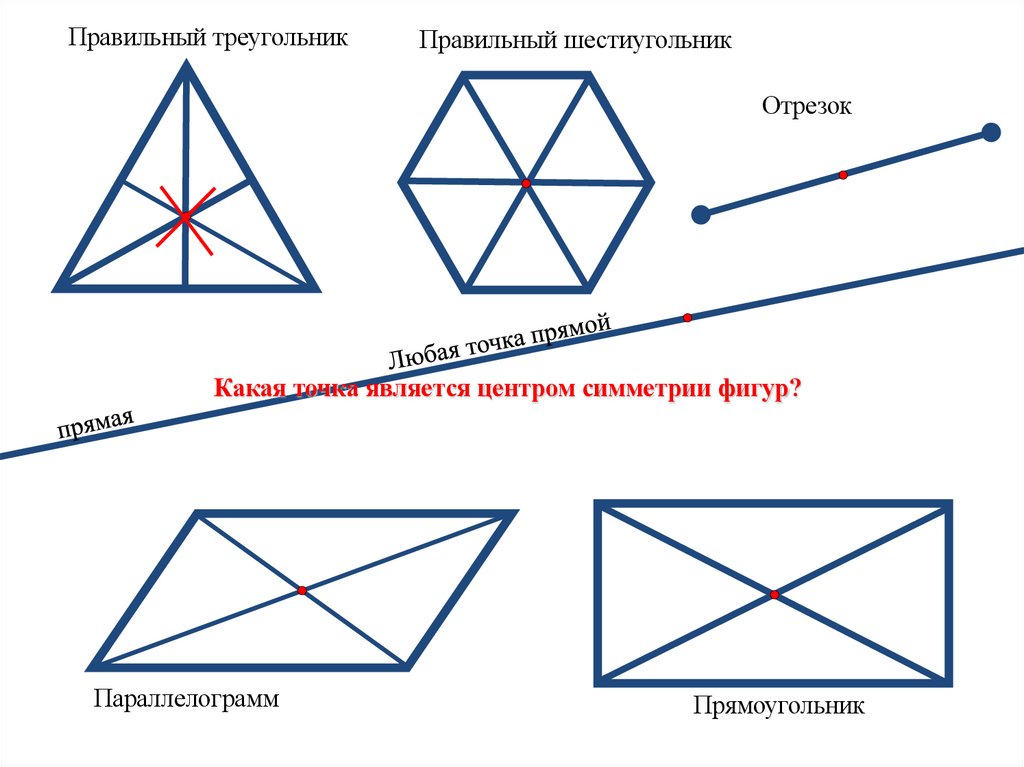
Правильный треугольник
Правильный шестиугольник
Отрезок
Какая точка является центром симметрии фигур?
Параллелограмм
Прямоугольник

22.

Фигура называется симметричной относительно точки О,
если для каждой точки фигуры симметричная ей точка
относительно точки О также принадлежит этой фигуре.
Какие буквы имеют центр симметрии?
S
О
Ф
Z
Х И

23.

24.

Причудливые формы в природе
http://www.lookatme.ru/flows/illy
ustratsiya/posts/36694-ernsthaeckel
Обладает ли центральной
симметрией 5-угольник?

25.

Причудливые формы в природе
Хотите увидеть больше? ВАМ
СЮДА:
http://www.lookatme.ru/flows/illy
ustratsiya/posts/36694-ernsthaeckel

26.

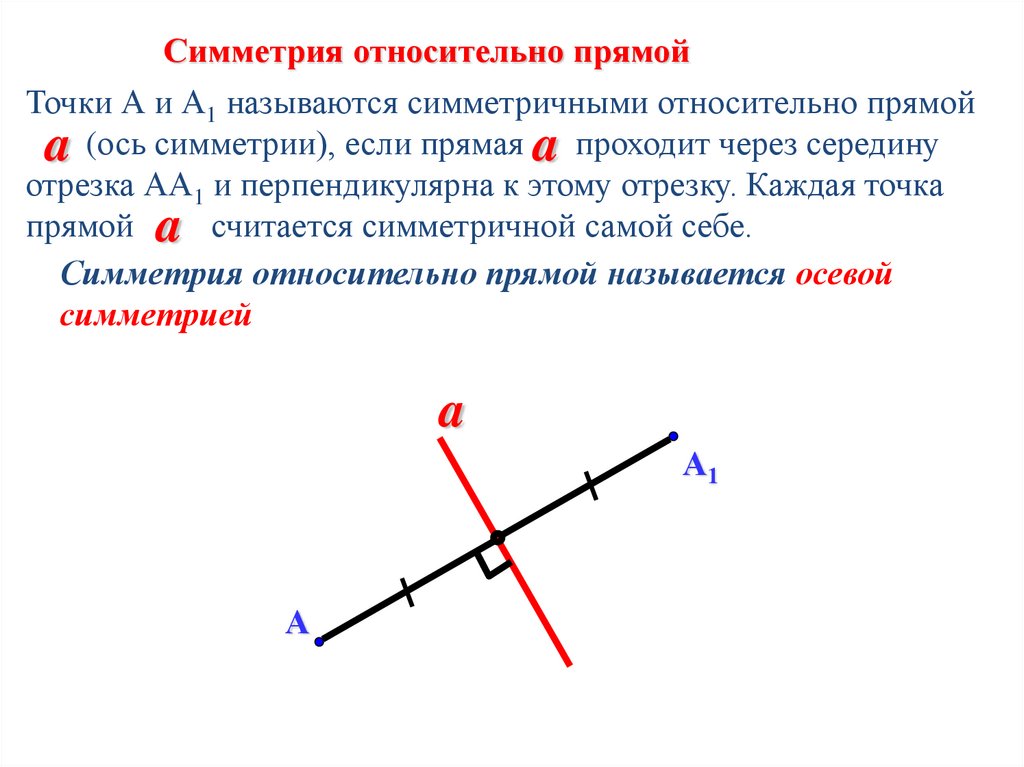
Симметрия относительно прямой
Точки А и А1 называются симметричными относительно прямой
a (ось симметрии), если прямая a проходит через середину
отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка
прямой a считается симметричной самой себе.
Симметрия относительно прямой называется осевой
симметрией
a
А1
А

27.

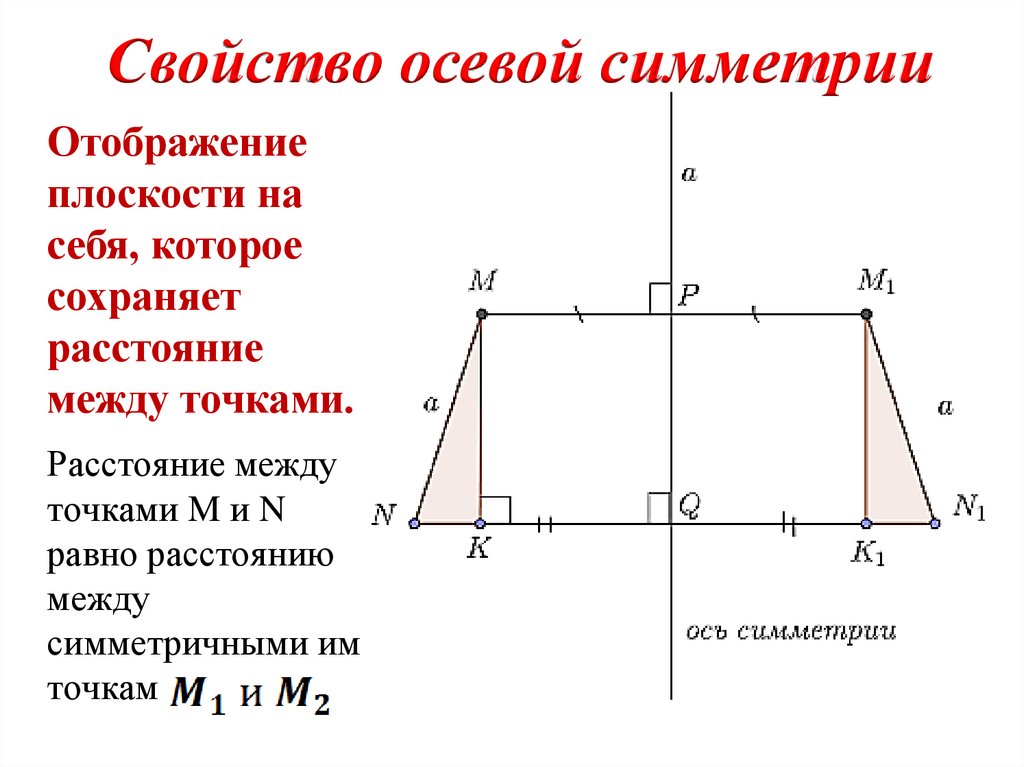
Свойство осевой симметрии
Отображение
плоскости на
себя, которое
сохраняет
расстояние
между точками.
Расстояние между
точками M и N
равно расстоянию
между
симметричными им
точкам

28.

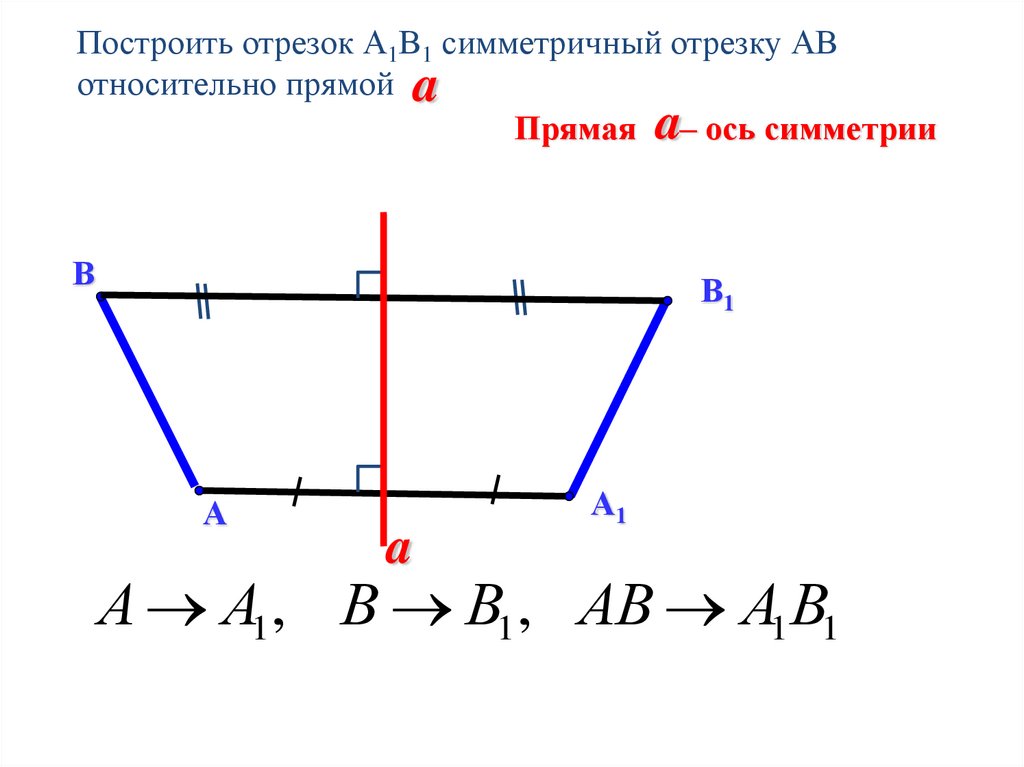
Построить отрезок А1В1 симметричный отрезку АВ
относительно прямой a
Прямая a– ось симметрии
В
В1
А
a
А1
А А1 , В В1 , АВ А1В1

29.

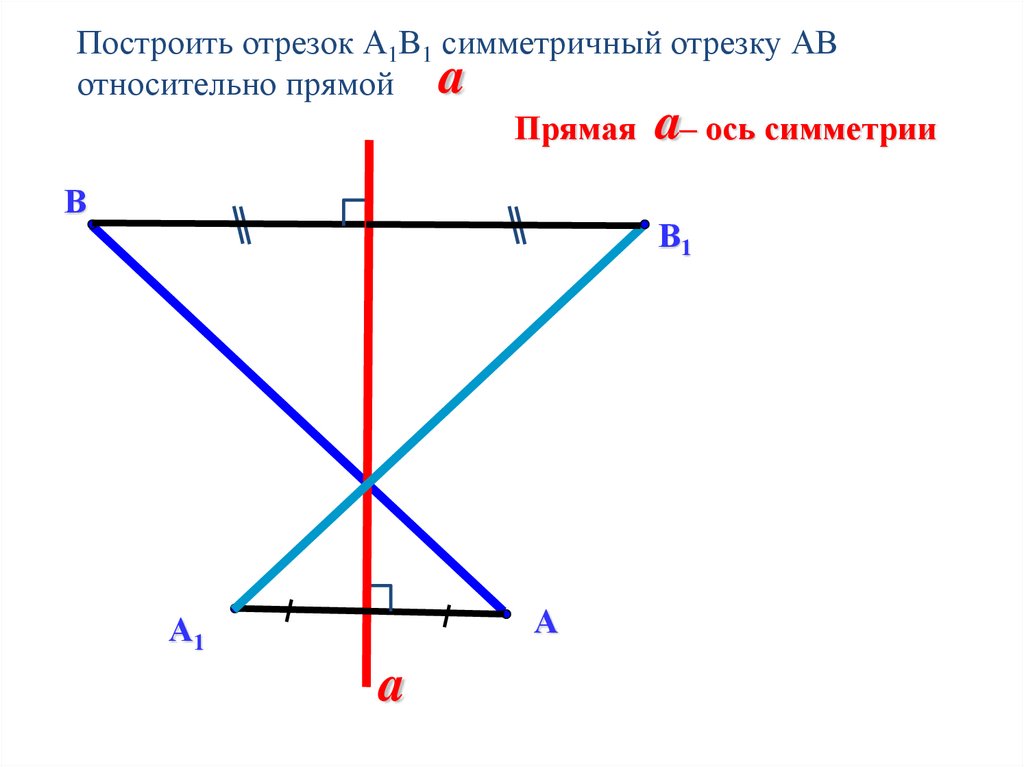
Построить отрезок А1В1 симметричный отрезку АВ
относительно прямой a
Прямая a– ось симметрии
В
В1
А
А1
a

30.

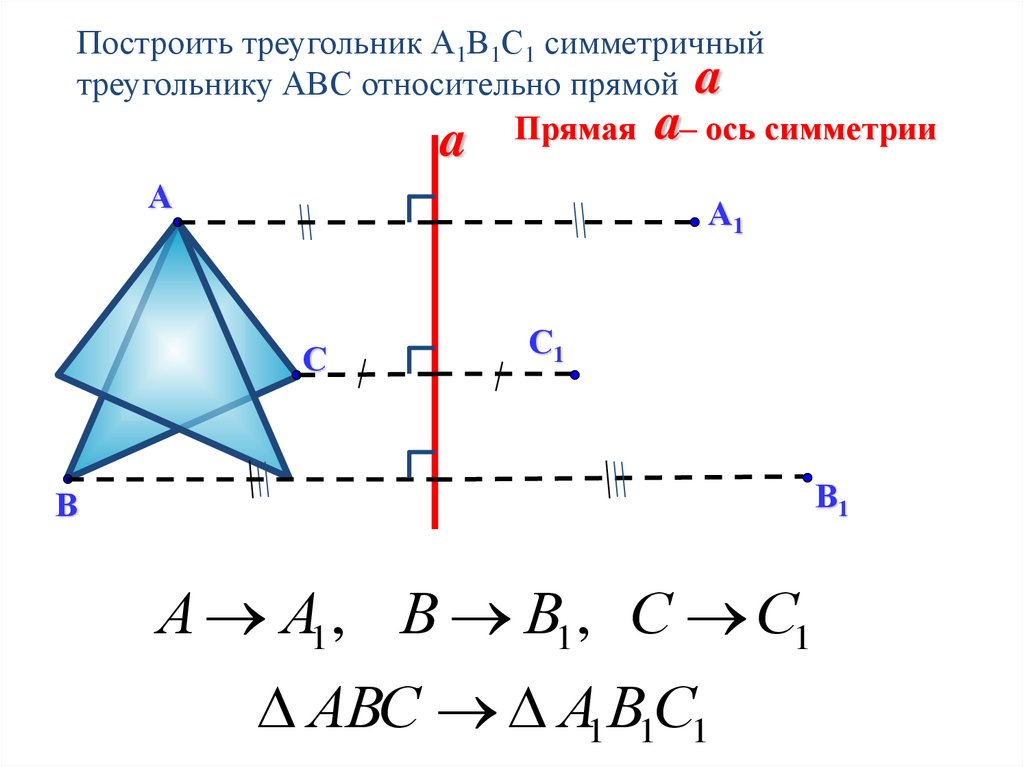
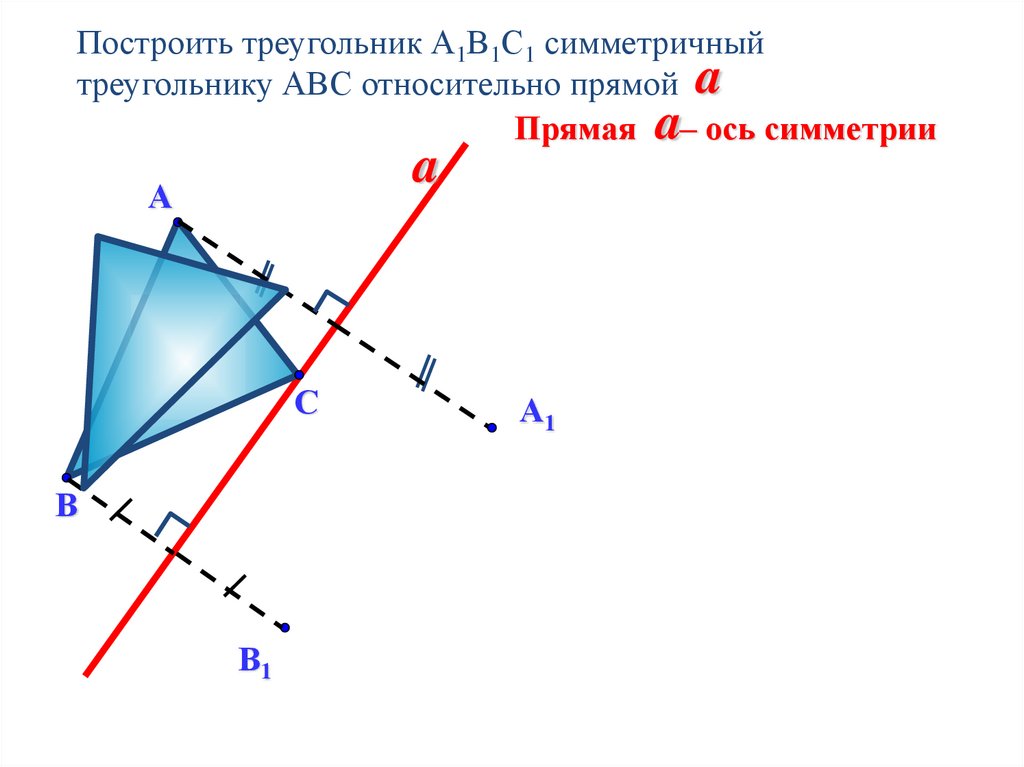
Построить треугольник А1В1С1 симметричный
треугольнику АВС относительно прямой a
a Прямая a– ось симметрии
А
А1
С
С1
В1
В
А А1 , В В1 , С С1
АВС А1В1С1

31.

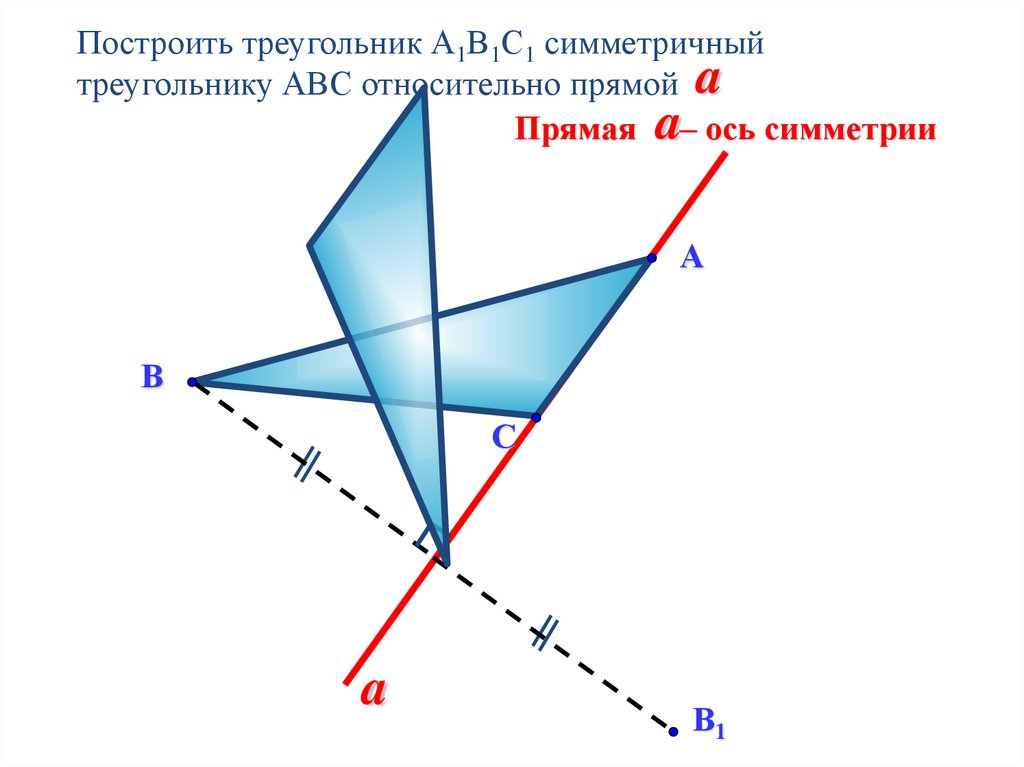
Построить треугольник А1В1С1 симметричный
треугольнику АВС относительно прямой a
Прямая a– ось симметрии
a
А
С
В
В1
А1

32.

Построить треугольник А1В1С1 симметричный
треугольнику АВС относительно прямой a
Прямая a– ось симметрии
А
В
С
a
В1

33.

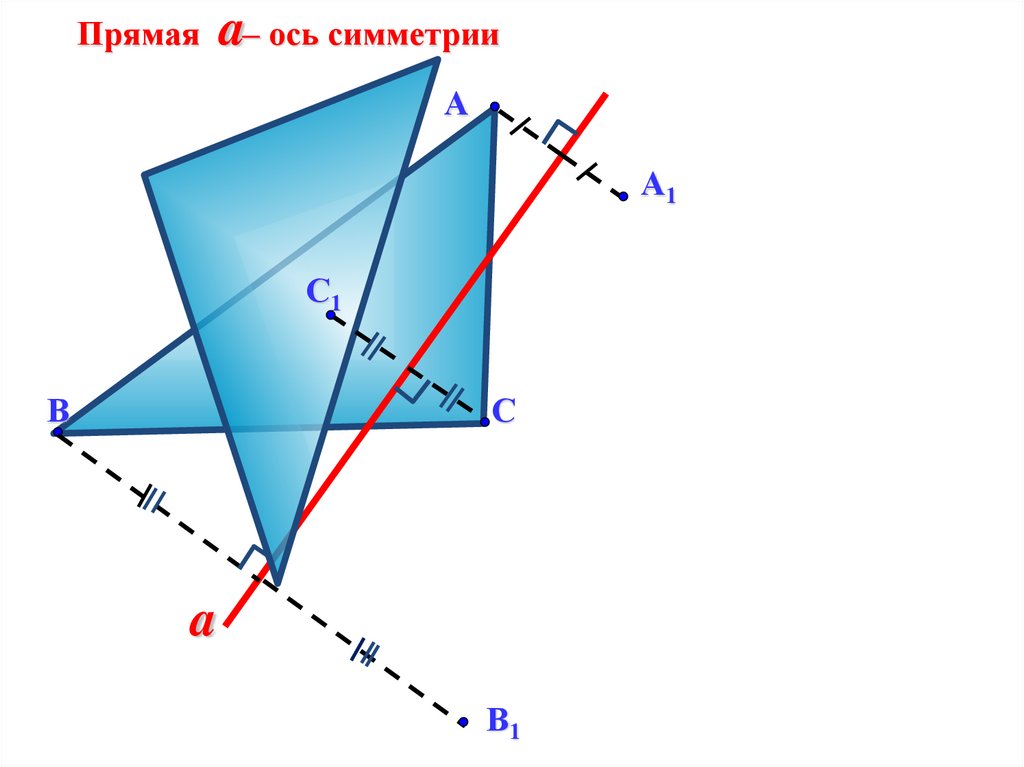
Прямая a– ось симметрии
А
А1
С1
В
С
a
В1

34.

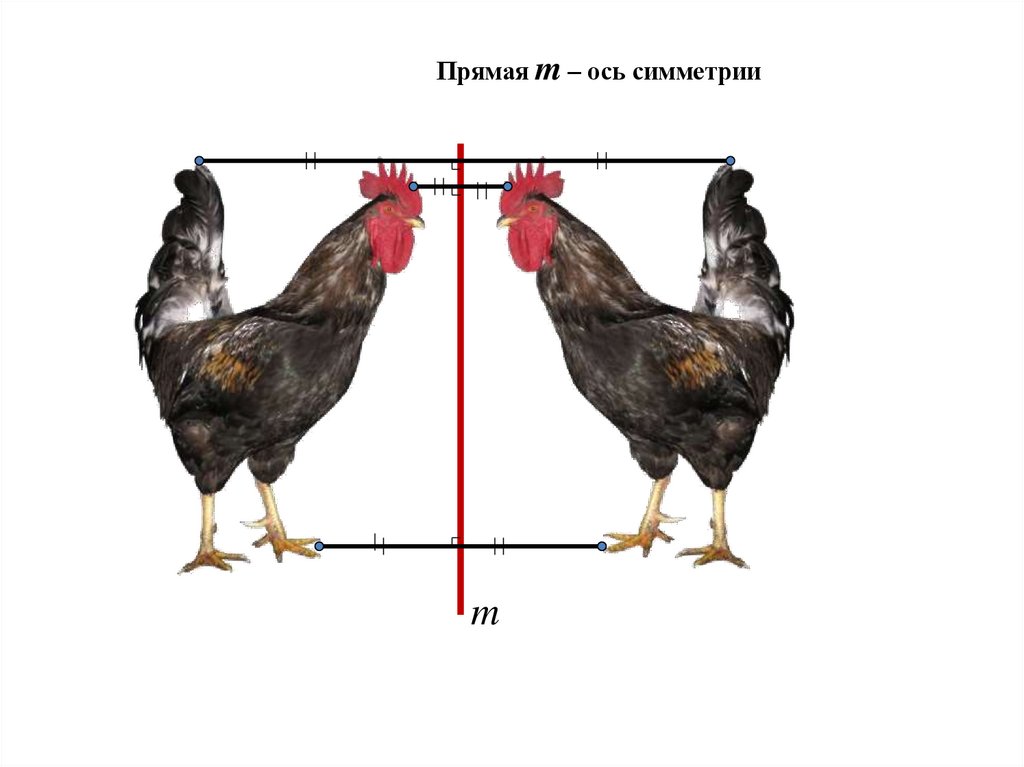
Прямая m – ось симметрии
m

35.

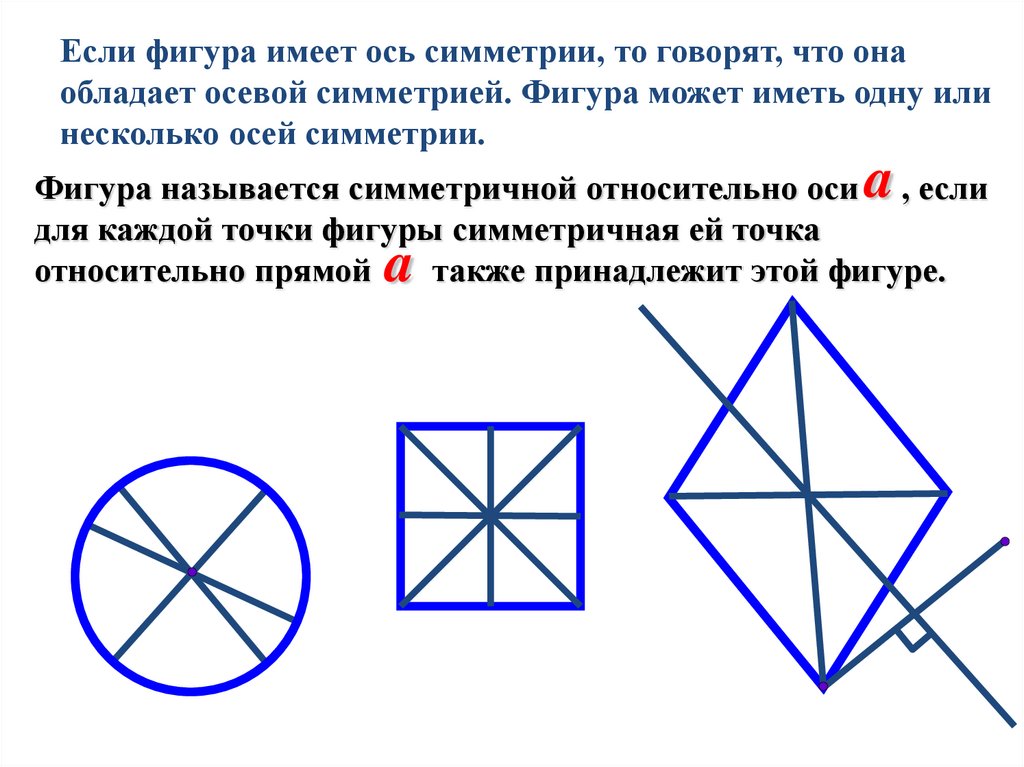
Если фигура имеет ось симметрии, то говорят, что она
обладает осевой симметрией. Фигура может иметь одну или
несколько осей симметрии.
a
Фигура называется симметричной относительно оси , если
для каждой точки фигуры симметричная ей точка
относительно прямой
также принадлежит этой фигуре.
a

36.

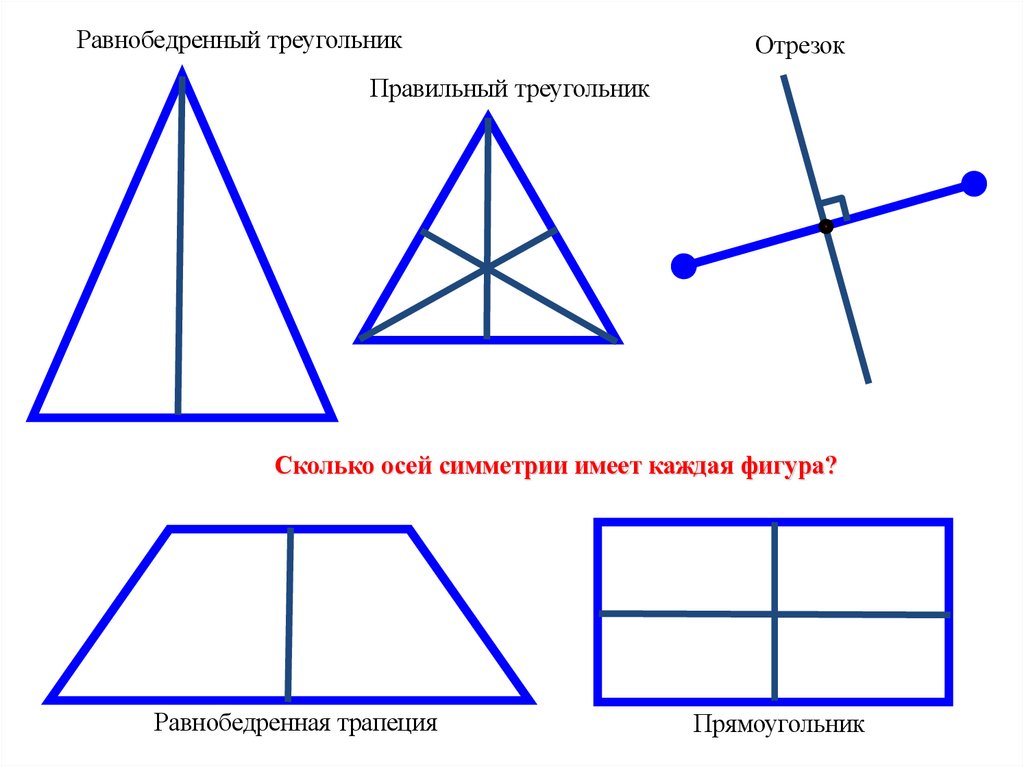
Равнобедренный треугольник
Отрезок
Правильный треугольник
Сколько осей симметрии имеет каждая фигура?
Равнобедренная трапеция
Прямоугольник

37.

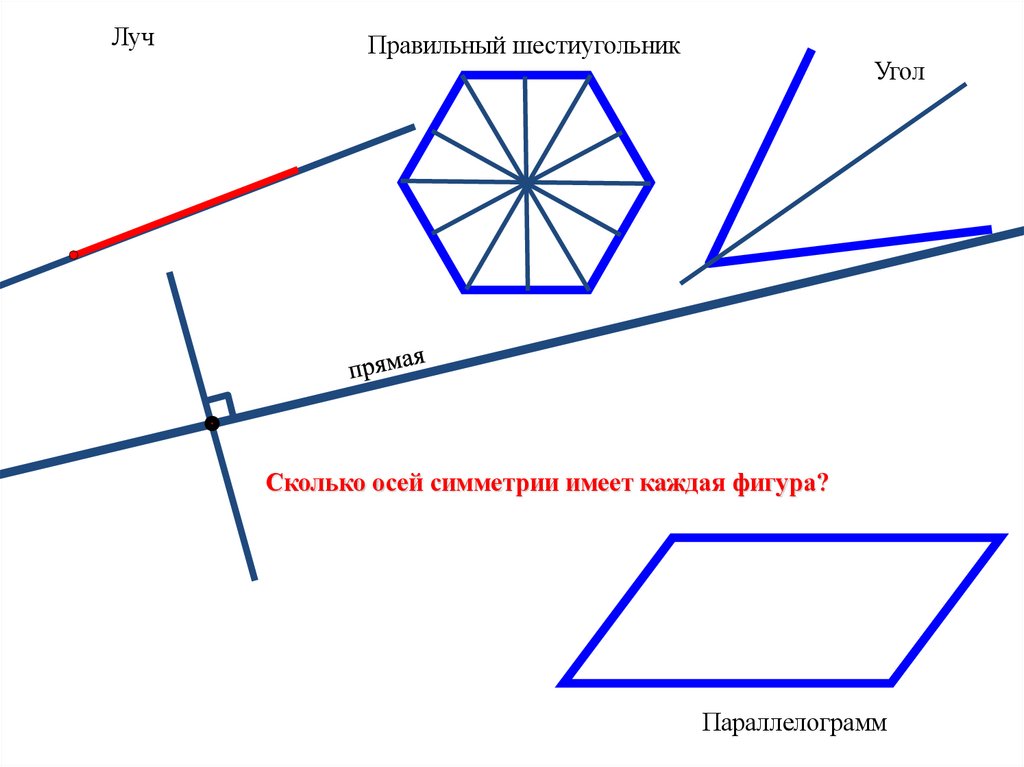
Луч
Правильный шестиугольник
Угол
Сколько осей симметрии имеет каждая фигура?
Параллелограмм

38.

Какие буквы имеют ось симметрии?
А БФ Г 0 Э
Ю ЖН П Ш

39.

Какие буквы имеют ось симметрии?
RYSV Х С
DWU М В

40.

Симметрия в природе

41.

Символ вечной любви, Индии, симметрии, торжества персидской
архитектуры - мавзолей Тадж-Махал

42.

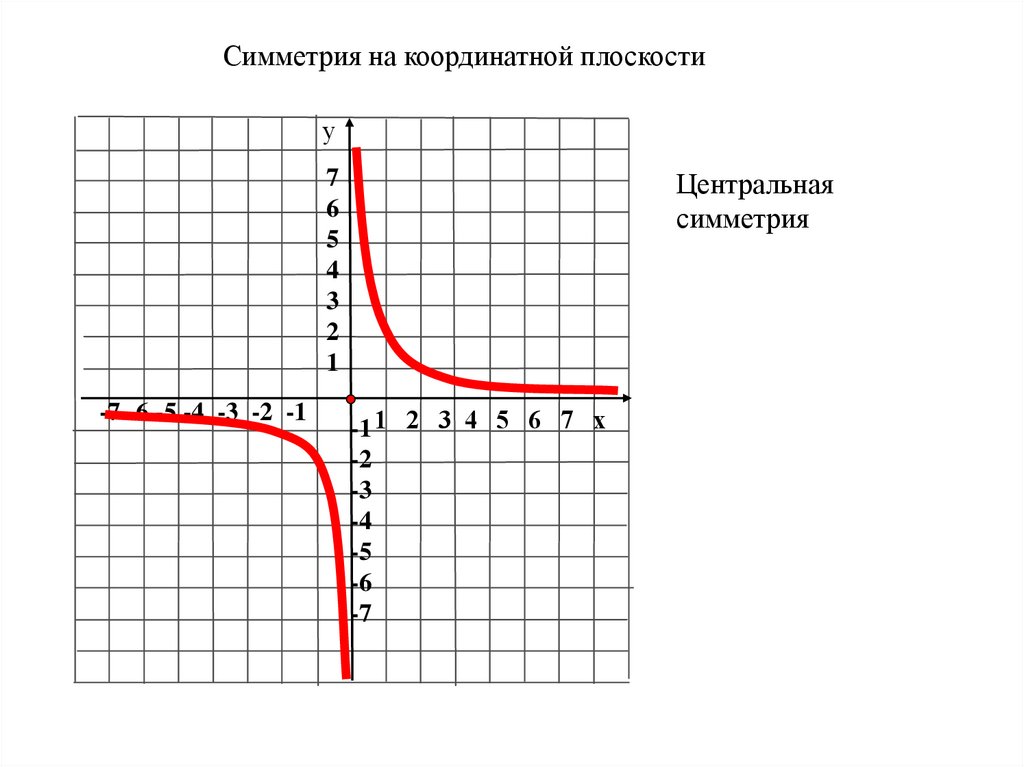
Симметрия на координатной плоскости
у
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
Центральная
симметрия
-1 1 2 3 4 5 6 7 х
-2
-3
-4
-5
-6
-7

43.

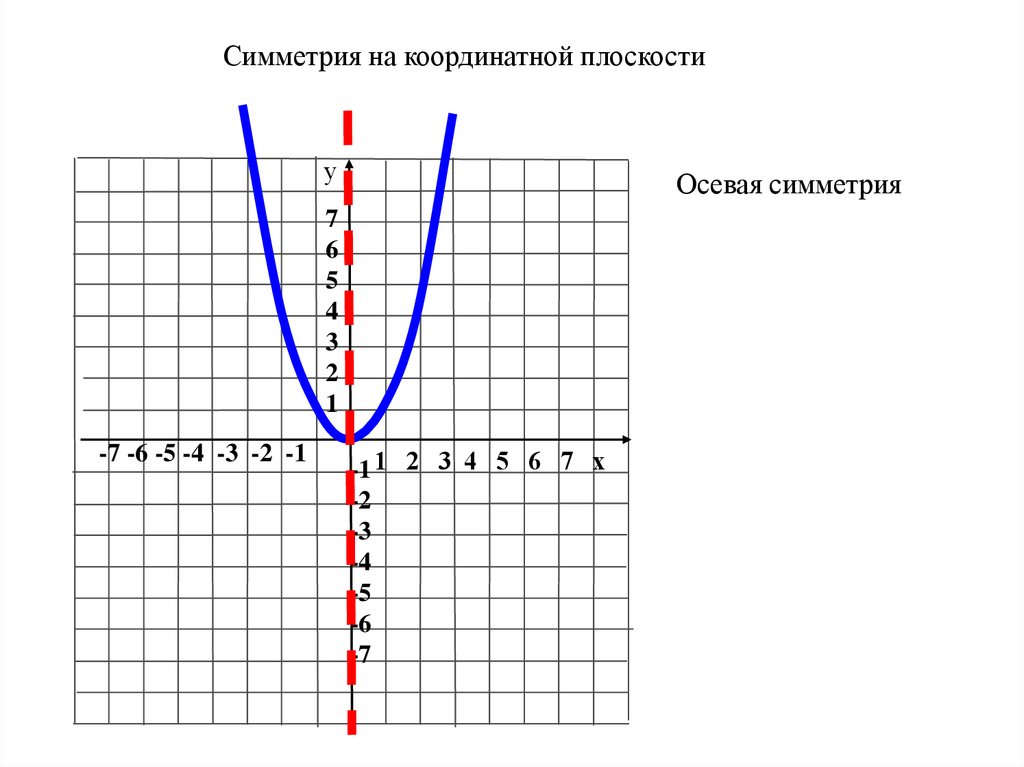
Симметрия на координатной плоскости
у
Осевая симметрия
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
-1 1 2 3 4 5 6 7 х
-2
-3
-4
-5
-6
-7

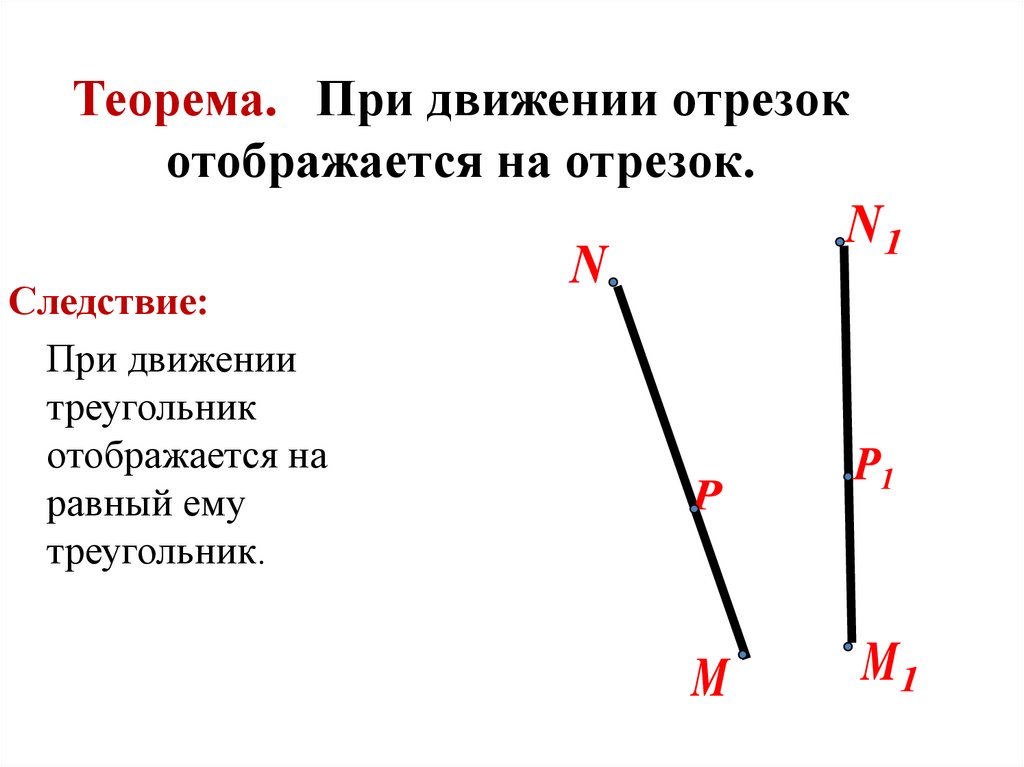
44. Теорема. При движении отрезок отображается на отрезок.

Следствие:
При движении
треугольник
отображается на
равный ему
треугольник.