Похожие презентации:
Понятия ДНФ, КНФ. Методика построения таблицы истинности для ДНФ упрощенным методом
1. Понятия ДНФ, КНФ. Методика построения таблицы истинности для ДНФ упрощенным методом
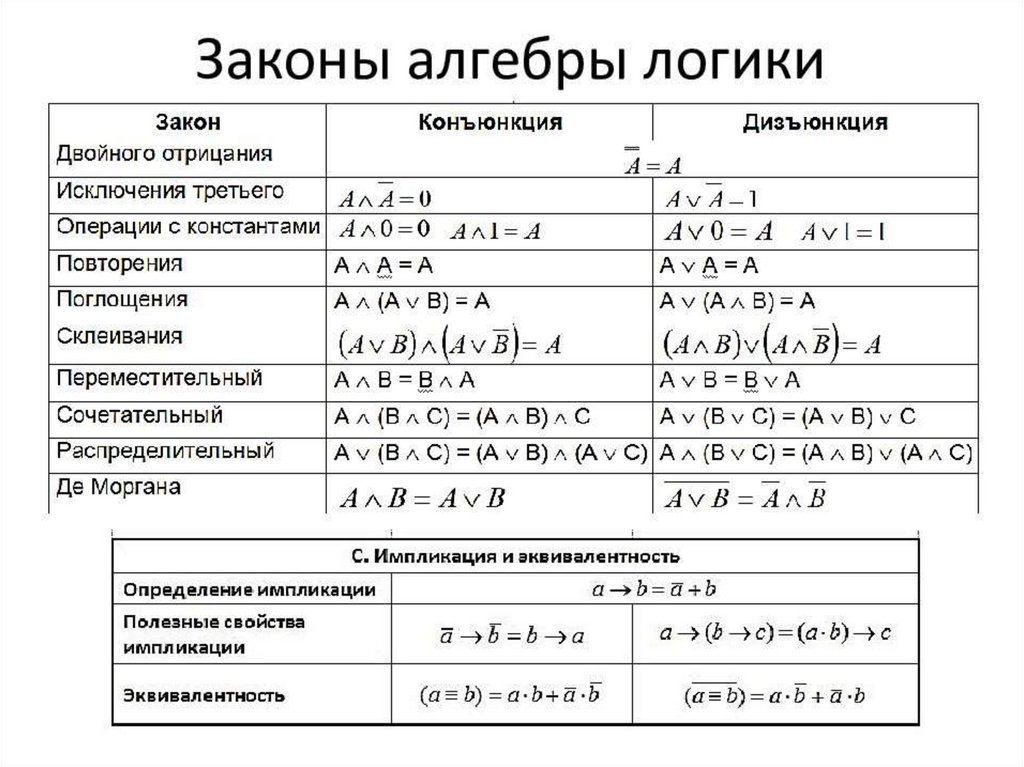
2. Нормальные формы для формул алгебры высказываний
ЛЕКЦИЯ 43.
Если логическое выражение содержит большое числоопераций, то составлять для него таблицу истинности
достаточно сложно, так как приходится перебирать большое
количество вариантов. В таких случаях формулы удобно
привести к нормальной форме.
Формула имеет нормальную форму, если в ней отсутствуют
знаки эквивалентности, импликации, двойного отрицания,
при этом знаки отрицания находятся только при логических
переменных.
В алгебре высказываний используют две нормальные
формы: дизъюнктивную (ДНФ) и конъюнктивную
нормальные формы (КНФ).
4.
ДНФОпределение. Элементарной конъюнкцией (или конъюнктом)
называется конъюнкция высказываний и/или их отрицаний.
A B C
В элементарной конъюнкции нет двух одинаковых переменных, так как
A A ≡ A.
Определение. Формула, представляющая собой дизъюнкцию
элементарных конъюнкций, называется дизъюнктивной
нормальной формой (ДНФ).
Например,
A B C A B A C
5.
КНФОпределение.
Элементарной
дизъюнкцией
(или
дизъюнктом) называется дизъюнкция высказываний и/или
их отрицаний.
Например,
A B C
В элементарной дизъюнкции нет двух одинаковых переменных,
так как А∨А ≡ А
Определение. Формула, представляющая собой конъюнкцию
элементарных дизъюнкций, называется конъюнктивной
нормальной формой (КНФ).
Например,
( A B C ) ( A B) ( A C )
6.
Алгоритм приведения к НФДля приведения формулы к нормальной форме
используют законы логики и правила логических
преобразований по следующему алгоритму:
1. Устранить «↔» и «→».
2. Продвинуть отрицание до переменной.
3. Постоянно избавляться от двойных отрицаний.
7.
8.
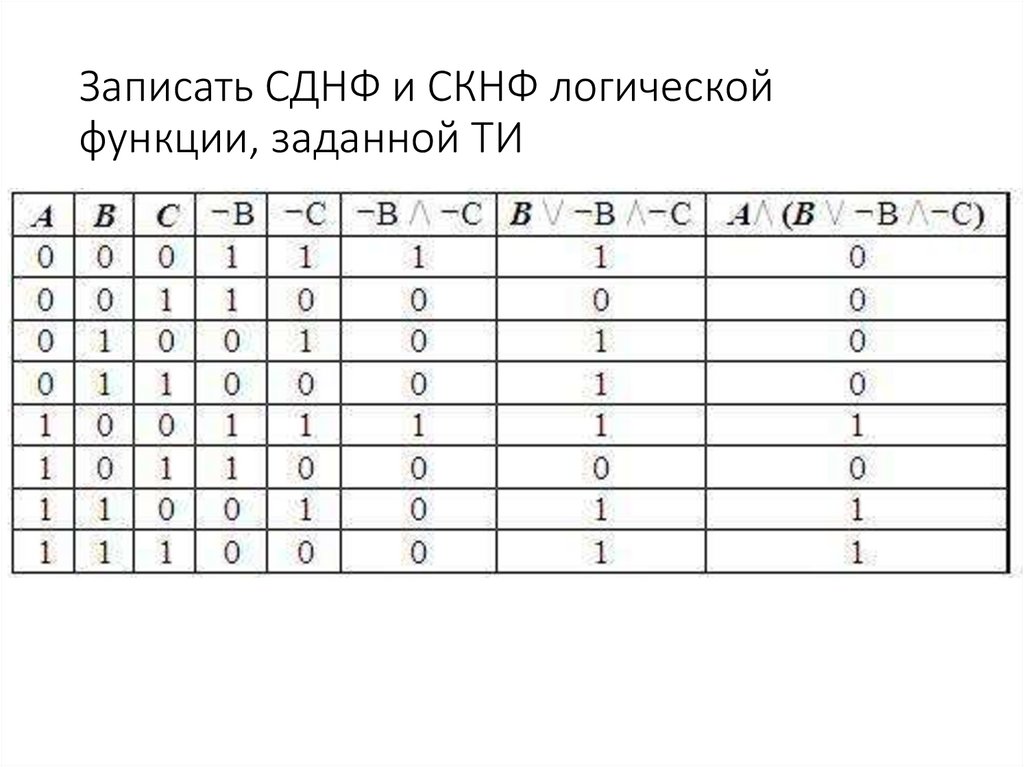
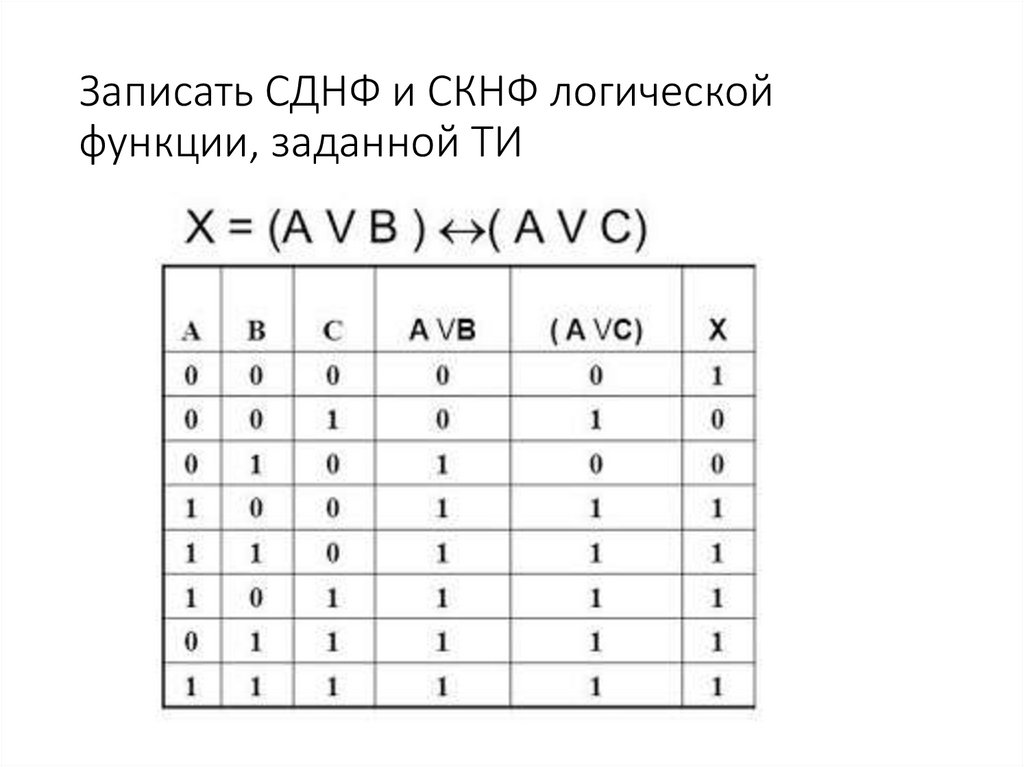
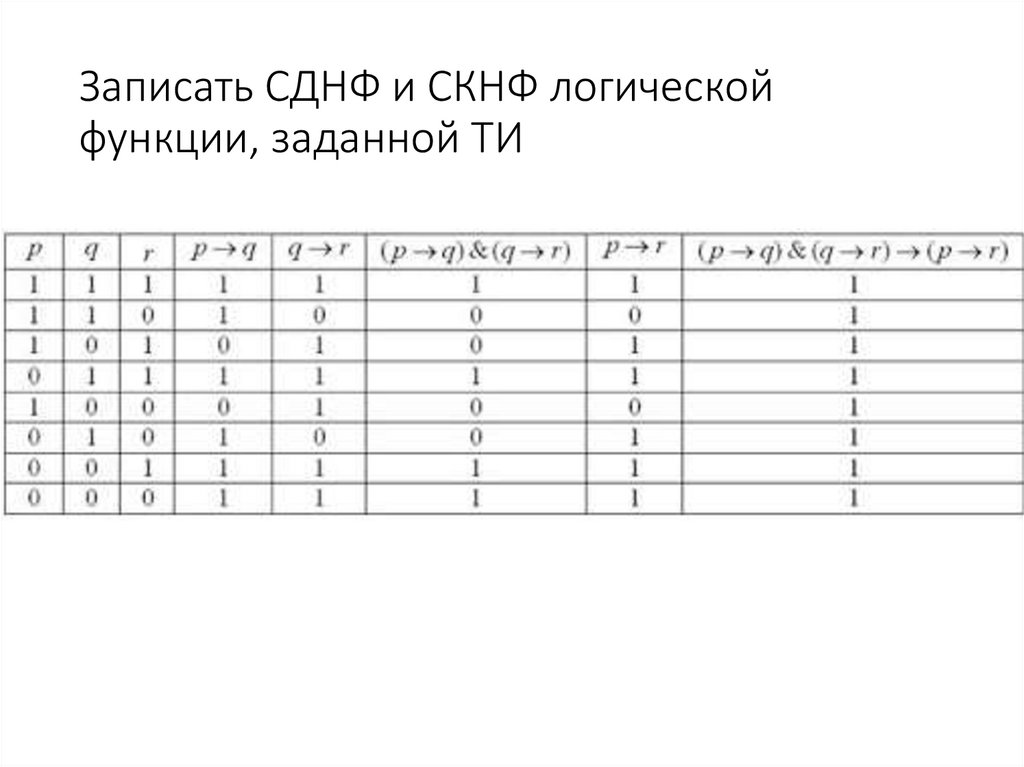
Примеры:1. Преобразовать формулу к виду ДНФ

























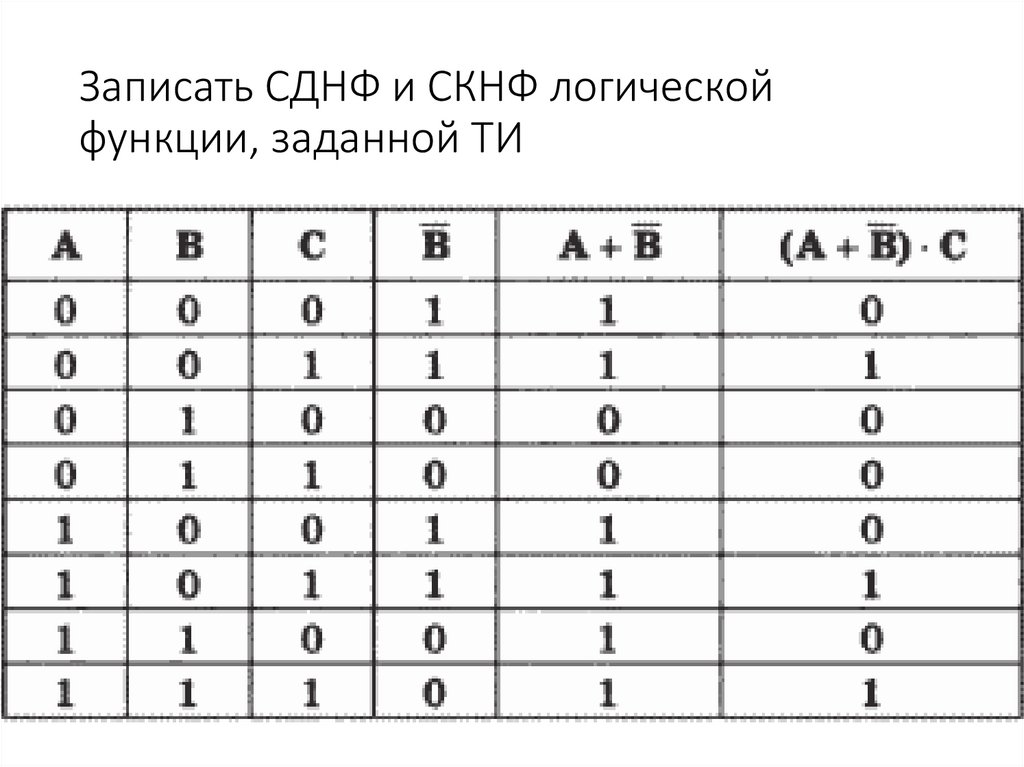



 Математика
Математика








