Булевы функци Тема2

1. ТЕМА:Булевы функции. Понятие булевой функции. Способы задания ДНФ, КНФ.

2. 1 Основные понятия алгебры логики

Математический аппарат, базирующийся на алгебре логики,
широко используется для описания функционирования, анализа
и синтеза цифровых схем.
Основным понятием алгебры логики является высказывание.
Высказыванием
называется
всякое
суждение
(утверждение),
которое
либо
истинно,
либо
ложно.
Одновременно истинным и ложным высказывание быть не
может.
Истинность высказывания обозначается единицей, а
ложность – нулем.
Простое высказывание не зависит от значений других
высказываний..

3.

Значение истинности сложного высказывания зависит
от истинности других высказываний, составляющих его.
Любое сложное высказывание можно считать логической
функцией от простых высказываний (аргументов).
Логическая функция, как и ее аргументы, принимает
только два значения: единица или нуль.
Множество символов X = {x1, х2,..., хn}, каждый из которых
принимает значения единица или нуль, называется
множеством переменных или аргументов.
Функция
f(x1, х2,..., хn), определенная на множестве
всевозможных наборов аргументов из X и принимающая
значения единица или нуль, называется функцией алгебры
логики или булевой функцией.

4.

Областью определения булевой функции служит
совокупность всевозможных n-мерных наборов из единиц и
нулей.
Приняты три способа задания булевых функций:
1. Формула, указывающая в явном виде последовательность
операций, производимых над переменными:
F f ( x1, x2 ,..., xn ).
2. Таблица
истинности,
в
левой
части
которой
перечисляются все возможные комбинации значений
аргументов x1, x2,..., хn, а в правой – значения функции. При
n переменных число строк таблицы равно 2n.
3. Логическая
схема
или
условное
графическое
изображение логической функции.

5.

Число различных функций алгебры логики, зависящих от n
2n
аргументов, конечно и равно 2 .
Значения функции могут быть заданы не на всех возможных
наборах аргументов. Функции, значения которых на некоторых
наборах не определены, называются не полностью
определенными.
Функция f ( x1,..., xi 1, xi , xi 1,..., xn ) существенно зависит
от аргумента xi, если имеет место соотношение
f ( x1,..., xi 1, 0, xi 1,..., xn ) f ( x1,..., xi 1, 1, xi 1,..., xn ).
В противном случае функция зависит от xi несущественно и
xi является ее фиктивным аргументом.

6. 2 Элементарные булевы функции

Элементарные булевы функции образуются путем
использования однородных связей между двоичными
переменными.
Существует одиннадцать элементарных функций, которые
часто употребляются в алгебре логике и ее приложениях.
1) Две функции, которые не зависят ни от одного аргумента
(n=0 ). Это f1 = 0 – константа нуль и f2 = l – константа
единица.
2) При n = 1 имеем две функции, существенно зависящие от
одного аргумента x. f3 = х - функцией прямой передачи
сигнала, f x - функцией отрицания или инверсии
4

7.

x
f3(x)
f4(x)
0
1
0
1
1
0
Значения f3(x) совпадают со
значением переменной х, а f4(x)
принимает
значения,
противоположные
значениям
переменной х.
Устройства, реализующие элементарные булевы функции,
называются логическими элементами.
Их входы соответствуют булевым переменным, а выход –
реализуемой функции. Для обозначения логических элементов
используют упрощенные изображения в виде прямоугольников,
внутри которых помещаются условные названия или символы
соответствующей функции.
Элемент НЕ (инвертор)
x
1
a
f3=x
x
f4=x
1
б

8.

Существует 10 функций, существенно зависящих от двух
аргументов x1 и х2.
x1
0
0
1
1
x2
0
1
0
1
f5
0
1
1
1
f6
0
0
0
I
f7
1
0
0
1
f8
1
1
0
1
f9
1
0
0
0
f10
1
1
1
0
f11
0
1
1
0
3) Функция f5(x1, x2)=x1\/x2 называется дизъюнкцией, или
логическим сложением x1 и x2. Читается «х1 или х2».

9.

4) Функция f 6 ( x1, x2 ) x1 x2 называется конъюнкцией,
или логическим умножением х1 и х2. Читается «x1 и х2».
5) Функция f7(x1, х2) = х1~х2 называется функцией
эквивалентности, или функцией равнозначности.
Читается «x1 эквивалентно х2».

10.

f8 ( x1, x2 ) x1 x2
6) Функция
называется функцией
импликации. Читается «если х1, то х2».
f 9 ( x1 , x2 ) x1 x2
7) Функция
называется функцией
Вебба, или стрелкой Пирса. Читается «ни x1 ни х2».

11.

f10 ( x1, x2 ) x1 | x2
8) Функция
называется функцией
Шеффера. Читается «неверно, что х1 и x2 ».
f11( x1, x2 ) x1 x2
9) Функция
называется функцией
сложения по модулю 2. Читается «х1 неравнозначно х2».
Функция принимает значение 1 только в том случае, если
переменные х1 и x2 имеют различные значения, и значение 0 в
противном случае.

12. 3 Полнота системы булевых функций

Одно из основных понятий алгебры логики - понятие
функциональной полноты системы булевых функций.
Система булевых функций называется функционально полной,
если она позволяет представить любую булеву функцию.
Логические элементы, соответствующие функционально
полным наборам булевых функций, образуют так называемый
базис и позволяют построить любую сколь угодно сложную
логическую схему.
Наиболее распространенными являются базисы И-ИЛИНЕ, ИЛИ-НЕ, И-НЕ.

13. 4 Законы и тождества алгебры логики

Законы алгебры логики устанавливают эквивалентность
логических формул, образованных с помощью полного набора
логических операций И, ИЛИ, НЕ.
1) Коммутативность дизъюнкции и конъюнкции
x1\/x2 = x2\/x1, x1x2 = x2x1
2) Ассоциативности дизъюнкции и конъюнкции
x1\/( x2\/x3) = (x1\/x2)\/x3,
x1(x2x3) = (x1x2)x3
3) Идемпотентности дизъюнкции и конъюнкции
x\/x = х,
xx = x

14.

4)
Дистрибутивности
конъюнкции
относительно
дизъюнкции и дизъюнкции относительно конъюнкции
x1(x2\/x3) = x1x2\/x1x3,
x1\/ x2x3 = (x1\/x2)( x1\/x3)
5) де Моргана
x1 x2 x1 x2 ,
x1 x2 x1 x2 ;
6) Двойного отрицания
x x;
7) Склеивания
( x1 x2 )( x1 x2 ) x1,
x1x2 x1x2 x1;

15.

8) Поглощения
x1\/ x1x2 = x1, x1(x1\/x2) = x1
9) Действия с константами 0 и 1
x\/0 = х,
x·0 = 0,
x\/1 = 1
x·1 = х,
x x 1,
x x 0.
Правило 1. Если логическая сумма двоичных переменных
содержит хотя бы одну пару слагаемых, из которых одно есть
некоторая переменная, а другое – ее отрицание, то она является
тождественно истинной:
x1 x5 x4 x3 x4 1.

16.

Правило 2. Если логическое произведение двоичных
переменных содержит хотя бы одну пару сомножителей, из
которых один есть некоторая переменная, а другой – ее
отрицание, то оно является тождественно ложным
x1x2 x4 x3 x2 0.
Следует отметить, что законы де Моргана справедливы для
любого числа переменных:
x1 x2 ... xn x1 x2 ...xn ;
x1 x2 ...xn x1 x2 ... xn .

17. 5 Представление булевых функций дизъюнктивными и конъюнктивными нормальными формами

Любая логическая функция может выражаться различными
логическими формулами, являющимися эквивалентными.
Наиболее удобными для практического использования
являются нормальные формы представления сложных
логических функций.
Элементарной конъюнкцией Q называется логическое
произведение любого конечного числа переменных и их
отрицаний, причем каждая переменная встречается только
один раз. Число переменных, составляющих элементарную
конъюнкцию, называется ее рангом.

18.

Если логическое выражение содержит большое число
операций, то составлять для него таблицу истинности
достаточно сложно, так как приходится перебирать
большое количество вариантов. В таких случаях
формулы удобно привести к нормальной форме.
Формула имеет нормальную форму, если в ней
отсутствуют
знаки
эквивалентности,
импликации,
двойного отрицания, при этом знаки отрицания
находятся только при логических переменных.
В алгебре высказываний используют две нормальные
формы: дизъюнктивную (ДНФ) и конъюнктивную
нормальные формы (КНФ).

19.

ДНФ
Определение. Высказывательная форма, состоящая из
переменных
или
отрицательных
переменных,
применением только одной операции конъюнкции,
называется
элементарной
конъюнкцией
(или
A B C
конъюнктом).
Например,
В элементарной конъюнкции нет двух
пропозициональных переменных, так как A A ≡ A.
одинаковых
Определение. Высказывательная форма, состоящая из
элементарных конъюнкций, применением только одной
операции дизъюнкции называется дизъюнктивной
нормальной формой (ДНФ).
Например, A B C A B A C

20.

КНФ
Определение. Высказывательная форма, состоящая
из
переменных
или
отрицания
переменных
применением только одной операции дизъюнкции,
называется
элементарной
дизъюнкцией
(или
A B C
дизъюнктом).
Например,
В элементарной дизъюнкции
нет двух
пропозициональных переменных, так как А∨А ≡ А
одинаковых
Определение. Высказывательная форма, состоящая из
элементарных дизъюнкций, применением только одной
операции конъюнкции называется конъюнктивной
нормальной формой (КНФ).
Например,( A B C) ( A B) ( A C)

21.

Алгоритм приведения к НФ
Для приведения формулы к нормальной форме
используют законы логики и правила логических
преобразований по следующему алгоритму:
1. Устранить «↔» и «→».
2. Продвинуть отрицание до пропозициональной
переменной.
3. Применить закон дистрибутивности.
4. Постоянно
избавляться
от
двойных
отрицаний.

22.

23.

24.

Совершенные НФ
Использование нормальных форм не устраняет полностью
неоднозначности записи логических функций, например
F ( A, B, C ) A B A C A B C
F ( A, B, C ) A B A C B C
F(A,B,C)=A B A C
Поэтому среди нормальных форм выделяют такие, в
которых функции записываются единственным образом.
Их называют совершенными. Применяются совершенная
дизъюнктивная и совершенная конъюнктивная формы
(СДНФ и СКНФ).

25.

СДНФ
Совершенная дизъюнктивная нормальная форма
(СДНФ) - ДНФ, удовлетворяющая условиям:
1. Все элементарные конъюнкции различны.
2. Нет нулевых конъюнкций.
3. Ни одна из элементарных конъюнкций не
повторяется.
4. Каждая элементарная конъюнкция содержит все
переменные или их отрицания.
Примеры СДНФ:
(X Y) ( X Y) (X Y)
(X Y Z) ( X Y Z) (X Y Z) (X Y Z) (X Y Z)
(X1 X2 X3 X4) ( X1 X2 X3 X4) (X1 X2 X3 X4)

26.

СКНФ
Совершенная конъюнктивная нормальная
форма (СДНФ): КНФ - удовлетворяющая
условиям:
1. Все элементарные дизъюнкции различны.
2. Нет нулевых дизъюнкций.
3. Ни одна из элементарных дизъюнкций не
повторяется.
4. Каждая элементарная дизъюнкция
содержит все переменные или их
отрицания.

27.

Теорема 1 (о представлении формулы алгебры
высказываний
совершенными
дизъюнктивными
нормальными формами). Каждая не тождественно
ложная формула алгебры высказываний от n аргументов
имеет единственную (с точностью до перестановки
дизъюнктивных членов) СДНФ.
Теорема 2 (о представлении формулы алгебры
высказываний
совершенными
конъюнктивными
нормальными формами). Каждая не являющаяся
тавтологией формула алгебры высказываний от n
аргументов имеет единственную (с точностью до
перестановки конъюнктивных членов) СКНФ.
Единственность совершенных нормальных форм у выполнимой ПФ
обуславливает их использование для доказательства равносильностей, идея
которого состоит в следующем: если у двух ПФ их СДНФ (СКНФ) совпадают, то
они равносильны.

28. Приведение формулы алгебры высказываний к совершенной нормальной форме  

Приведение формулы алгебры
высказываний к совершенной нормальной
форме
Способы приведения формул к совершенным
формам следуют из способов задания формул
алгебры высказываний – либо с помощью
таблицы, либо аналитически.

29.

Аналитический способ приведения к
совершенным формам
Для приведения ПФ к СДНФ выполняются равносильные
преобразования,
описанные
следующей
последовательностью шагов:
1. С помощью равносильных преобразований привести
ПФ к ДНФ.
2. Те
элементарные
конъюнкции,
в
которые
сомножителями входят не все переменные, умножить
на единицы, представленные в виде дизъюнкций
каждой недостающей переменной с ее отрицанием.
3. Раскрыть
скобки
по
соответствующему
дистрибутивному закону.
4. Для получения искомой СДНФ исключить повторения.

30.

Аналитический способ приведения к
совершенным формам
Приведение к СКНФ осуществляется аналогично, но
только к элементарным дизъюнкциям, содержащим
слагаемыми не все переменные, прибавляют нули,
представленные в виде конъюнкций каждой недостающей
переменной с ее отрицанием.

31.

Пример
Пусть ПФ, содержащая переменные X, Y, Z, имеет ДНФ вида X Z Y Z
Используя аналитический способ привести к СДНФ.
Решение:
В соответствии с процедурой приведения к СДНФ умножим
первую и вторую конъюнкции на 1
1 Y Y
1 X X
X Z Y Z X Z (Y Y ) Y Z ( X X )
X Z Y X Z Y Y Z X Y Z X
X Z Y X Z Y Y Z X СДНФ

32.

Табличный способ приведения к
совершенным формам
Табличный способ приведения к СДНФ
1. Составить таблицу истинности данной формулы.
2. Рассмотреть те строки, в которых формула принимает
истинностное значение 1. Каждой такой строке поставить в
соответствие элементарную конъюнкцию, причем переменная,
принимающая значение 1, входит в нее без отрицания, а 0 – с
отрицанием.
3. Образовать дизъюнкцию всех полученных элементарных
конъюнкций, которая и составит СДНФ.
Табличный способ приведения к СКНФ
1. Составить таблицу истинности данной булевой функции.
2. Рассмотреть те строки, в которых формула принимает
истинностное значение 0. Каждой такой строке поставить в
соответствие элементарную дизъюнкцию, причем переменная,
принимающая значение 1, входит в нее с отрицанием, а 0 – без
отрицания.
3. Образовать конъюнкцию всех полученных элементарных
дизъюнкций, которая и составит СКНФ.

33.

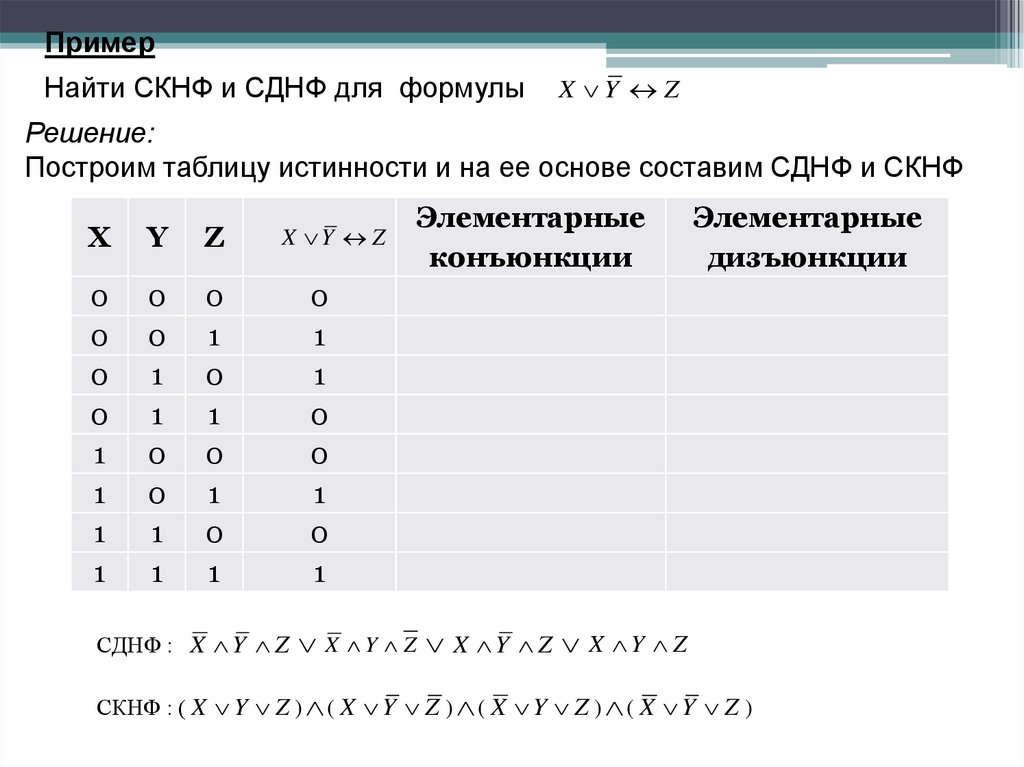
Пример
Найти СКНФ и СДНФ для формулы
X Y Z
Решение:
Построим таблицу истинности и на ее основе составим СДНФ и СКНФ
X
Y
Z
X Y Z
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
0
1
Элементарные
конъюнкции
Элементарные
дизъюнкции
СДНФ : X Y Z X Y Z X Y Z X Y Z
СКНФ : ( X Y Z ) ( X Y Z ) ( X Y Z ) ( X Y Z )

34.

Критерии тождественной истинности и
тождественной ложности формул алгебры
высказываний
Теорема 3 (признак тождественной истинности
формулы). Формула алгебры высказываний тождественно
истинна тогда и только тогда, когда в каждой элементарной
дизъюнкции её КНФ имеется, по меньшей мере, одна
пропозициональная переменная, входящая в этот
одночлен вместе со своим отрицанием.
Теорема4 (признак тождественной ложности формулы).
Формула алгебры высказываний тождественно ложна тогда
и только тогда, когда в каждой элементарной конъюнкции
её
ДНФ
имеется,
по
меньшей
мере,
одна
пропозициональная переменная, входящая в этот
одночлен вместе со своим отрицанием.

35.

Примеры:
1. Показать, что формула (P (P Q)) Q - тавтология
(P (P Q)) Q ( P ( P Q)) Q P ( P Q) Q
P (P Q) Q ( P P Q) ( P Q Q).
По теорем 2.6.1 формула тождественно истинна.

36.

Примеры:
2. Показать, что формула P ( Q ( P Q)) –
тождественно ложна
P ( Q ( P Q)) (P Q P) ( (P Q Q).
По теорем 2.6.2 формула тождественно ложна.

37.

Дизъюнктивной
нормальной
формой
называется дизъюнкция элементарных конъюнкций:
(ДНФ)
N Q1 Q2 ... Qk .
Любая булева функция может быть представлена в ДНФ
f ( x1, x2 , x3 ) x1x2 x3 x1x3 x2 .
Элементарной дизъюнкцией D называется логическая
сумма конечного числа переменных и их отрицаний, причем
каждая переменная встречается в сумме один раз. Число
переменных, составляющих элементарную дизъюнкцию,
называется ее рангом.
D x1 x2 x3 x4

38.

Конъюнктивной
нормальной
формой
называется конъюнкция элементарных дизъюнкций:
(КНФ)
K D1 D2 ... Dn .
Любую булеву функцию можно представить в КНФ
f ( x1, x2 , x3 ) ( x1 x2 x3 )( x1 x3 )( x2 x3 ).
Одна и та же логическая функция путем эквивалентных
преобразований может быть представлена различными ДНФ
или КНФ.
Единственность представления обеспечивают совершенные
нормальные формы.

39.

Совершенной ДНФ (СДНФ) логической функции f ( x1, x2 , xn )
от n различных переменных называется ДНФ, которая содержит
только конъюнкции ранга n и не содержит одинаковых
конъюнкций.
Произвольная логическая функция f ( x1 , x2 , , xn ) приводится
к СДНФ в следующей последовательности:
1) Функция f приводится к какой-либо ДНФ;
2) Конъюнкции, не содержащие всех двоичных переменных,
дополняются до конъюнкций n-го ранга;
3) Из полученной ДНФ с конъюнкциями n-го
удаляются повторяющие друг друга конъюнкции.
ранга

40.

Пример 1. Привести функцию к СДНФ.
f ( x1, x2 , x3 ) x1x2 x1x2 x3 x1x3
Решение: Дополним конъюнкции второго ранга
конъюнкций третьего ранга, используя закон склеивания:
до
x1x2 x1x2 x3 x1x2 x3
x1x3 x1x2 x3 x1x2 x3.
Просуммируем конъюнкции:
f ( x1 , x2 , x3 ) x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3
x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 .

41.

Если логическая функция задана таблицей истинности, то
построение СДНФ осуществляется по следующему алгоритму:
1) Выбираются наборы аргументов, на которых функция
обращается в единицу;
2) Выписываются конъюнкции, соответствующие этим
наборам, причем если аргумент хi входит в набор как единица,
то в конъюнкцию он вписывается без изменения. Если же
аргумент хi входит в данный набор как нуль, то в
соответствующую конъюнкцию вписывается его отрицание;
3) Все выписанные конъюнкции соединяют знаком
дизъюнкции.
Элементарные
конъюнкции
СДНФ
называют
конституэнтами единицы.

42.

Пример 2. Построить СДНФ для функции, заданной
таблично.
Х1
0
0
0
Х2
0
0
1
Х3 f(х1, х2, x3)
0
0
1
1
0
1
0
1
1
1
1
1
0
0
1
1
1
0
1
0
1
0
1
1
0
1
Функция f принимает значение
единица пять раз, поэтому ее СДНФ
представляет собой логическую сумму
пяти
элементарных
конъюнкций
третьего ранга
f ( x1, x2 , x3 ) x1x2 x3 x1x2 x3 x1x2 x3 x1x2 x3 x1x2 x3 .

43.

Совершенной КНФ (СКНФ) логической функции f от n
различных переменных называется КНФ, которая содержит
только дизъюнкции ранга n и не содержит одинаковых
дизъюнкций.
Построение СКНФ по таблично заданной функции
осуществляется в следующей последовательности:
1) Выбираются наборы аргументов, на которых функция
обращается в нуль;
2) Выписываются дизъюнкции, соответствующие этим
наборам, причем если аргумент хi входит в набор как нуль, то в
дизъюнкцию он вписывается без изменения. Если же аргумент хi
входит в данный набор как единица, то в соответствующую
дизъюнкцию вписывается его отрицание;
3) Все выписанные дизъюнкции соединяют знаком
конъюнкции.
Элементарные
дизъюнкции
СКНФ
называют
конституэнтами нуля.

44.

Пример 3. Построить СКНФ для функции f(x1, x2, x3),
заданной таблично.
Х1
0
0
0
Х2
0
0
1
Х3 f(х1, х2, x3)
0
0
1
1
0
1
0
1
1
1
1
1
0
0
1
1
1
0
1
0
1
0
1
1
0
1
Функция f принимает значение нуля
три раза, поэтому ее СКНФ представляет
собой
логическую
сумму
трех
элементарных дизъюнкций третьего
ранга
f ( x1, x2 , x3 ) ( x1 x2 x3 )( x1 x2 x3 )( x1 x2 x3 ).

45. 6. Синтез комбинационных схем

Под комбинационной схемой понимается техническое
устройство, предназначенное для преобразования дискретной
информации, причем значения выходных сигналов однозначно
определяются значениями входных сигналов в данный момент
времени. Предполагается, что в комбинационных схемах не
происходит задержки сигнала, а входные и выходные сигналы
могут принимать только значения единица и нуль (это могут
быть высокий и низкий уровни напряжения).
Синтезировать комбинационную схему – это означает на
основе заданного алгоритма работы построить структурную
схему минимальной сложности из логических элементов
заданного базиса.

46.

Синтез комбинационных схем осуществляется в три этапа:
1) Запись условий функционирования устройства (эти
условия могут быть заданы словесно, с помощью таблицы
истинности, либо с помощью логической функции);
2) Минимизация логической функции и приведение ее к
заданному базису;
3) Составление структурной схемы устройства.
Пример 4. Синтезировать комбинационную
реализующую булеву функцию в базисе И-ИЛИ-НЕ.
Рассмотреть переход к базисам И-НЕ и ИЛИ-НЕ.
f ( x1, x2 , x3 ) ( x1 / x2 ) ( x3 x1 )
схему,

47.

Представим функцию в ДНФ. Для этого используем формулы
x1 / x2 x1 x2 ;
x1 x2 x1 x2 ;
x1 x2 x1 x2 x1 x2 .
Тогда
f ( x1 , x2 , x3 ) x1 x2 ( x3 x1 )
x1 x2 ( x3 x1 ) x1 x2 ( x3 x1 )
( x1 x2 )x3 x1 x1 x2 ( x3 x1 )
x1 x3 x1 x2 x3 x1 x2 x3 x1 x2
x1 x3 x1 x2 .

48.

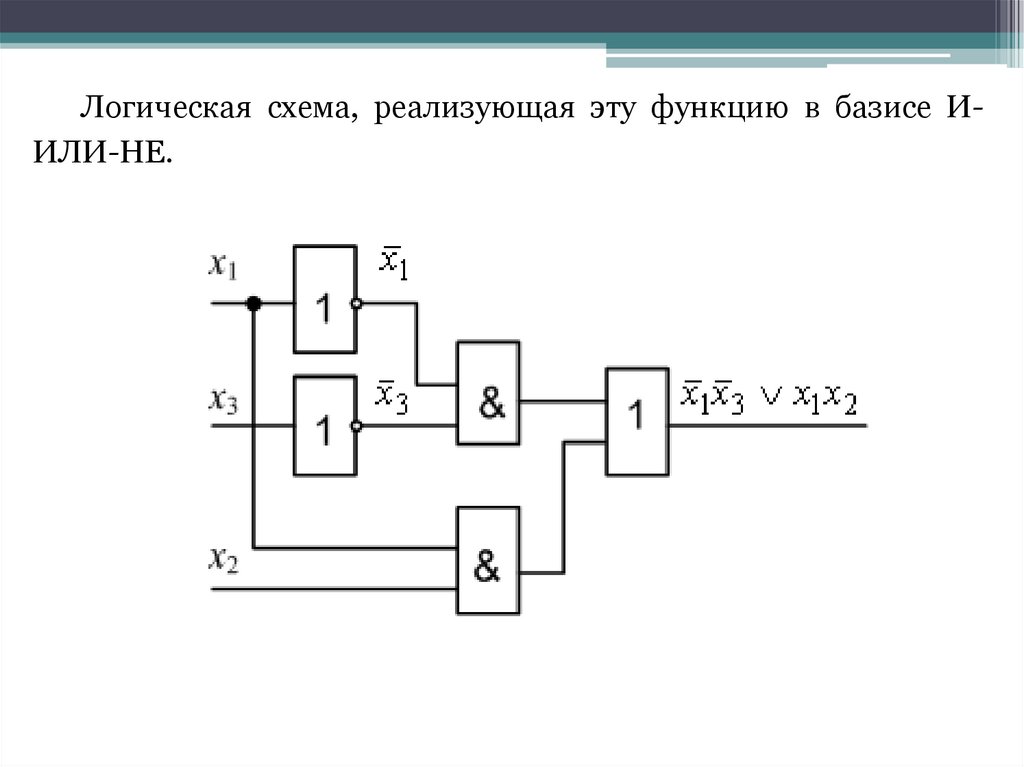
Логическая схема, реализующая эту функцию в базисе ИИЛИ-НЕ.

49.

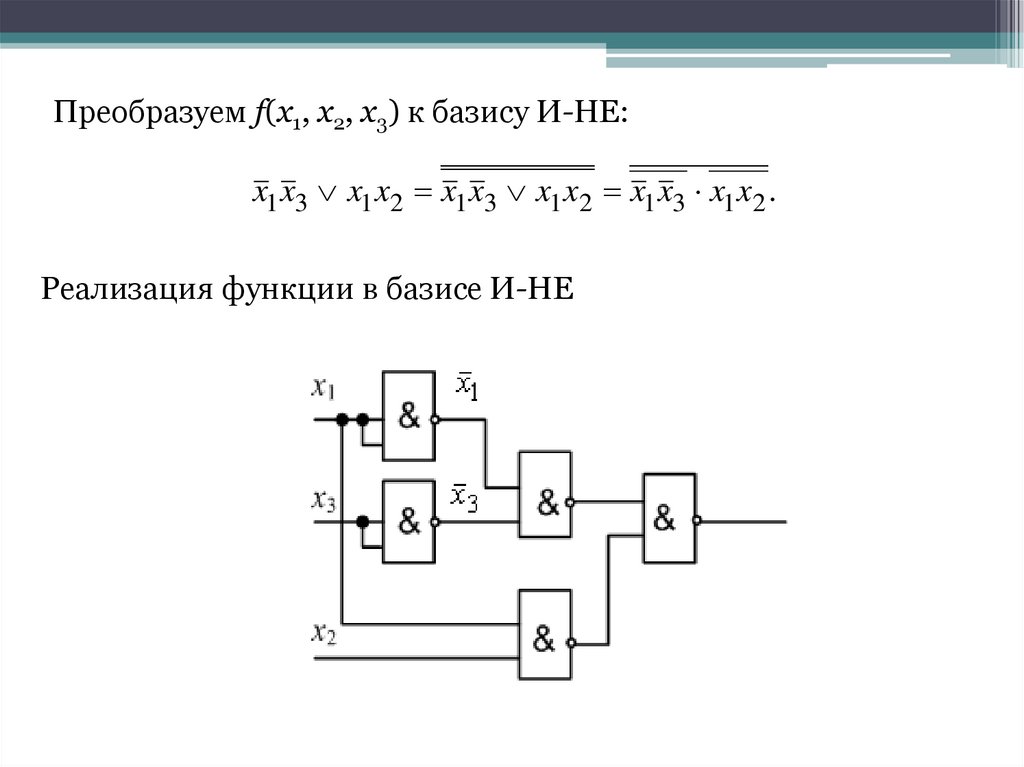
Преобразуем f(x1, x2, x3) к базису И-НЕ:
x1 x3 x1 x2 x1 x3 x1 x2 x1 x3 x1 x2 .
Реализация функции в базисе И-НЕ

50.

Преобразуем f (x1, x2, x3) к базису ИЛИ-НЕ:
x1x3 x1x2 x1x3 x1x2 x1 x3 x1 x2 x1 x3 x1 x2 .
x1
x3
1
1
x2
1
x1 x3
x1
1
x2
x1 x2
1
f ( x1 x2 x3 )
1
f ( x1 x2 x3 )

51.

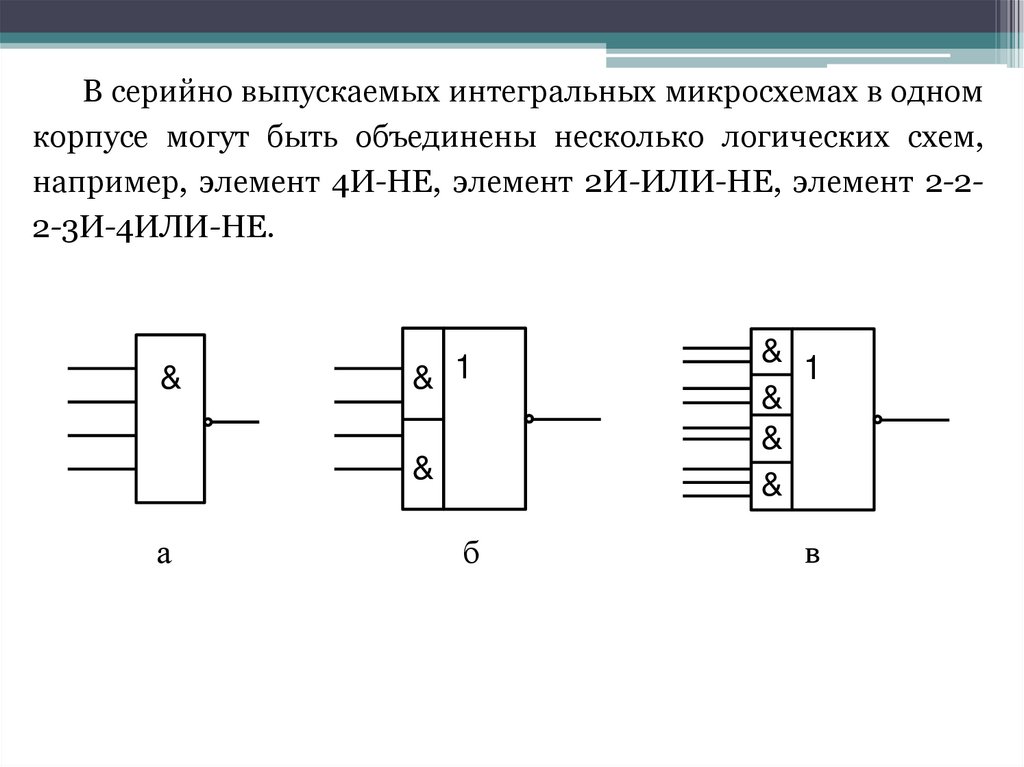
В серийно выпускаемых интегральных микросхемах в одном
корпусе могут быть объединены несколько логических схем,
например, элемент 4И-НЕ, элемент 2И-ИЛИ-НЕ, элемент 2-22-3И-4ИЛИ-НЕ.
&
& 1
&
а
б
&
1
&
&
&
в