Перпендикулярність прямих і площин в просторі

1. Презентація на тему

Перпендикулярність
прямих і площин в
просторі

2. план

перпендикулярність прямих
перпендикулярність прямої і площини
перпендикуляр і похила до площини
кут між прямою і площиною
перпендикулярні площини
ортогональне проектування
самостійна робота
тести

3. Перпендикулярність прямих

Дві прямі називаються
a
перпендикулярними, якщо кут
між ними дорівнює 90°.
b
до плану

4.

Кутом між мимобіжними прямими
називається кут між прямими, які
перетинаються і паралельні даним
мимобіжним.
b
b′
a
a′

5. теорема:

Якщо дві прямі, які
a
b
α
a´
b´
β
перетинаються,
паралельні двом
іншим прямим, що
перетинаються, то
кут між першими
прямими дорівнює
куту між другими
прямими.

6. Перпендикулярність прямої і площини (означення)

Пряма називається
a
b
O
c
α
d
до плану
перпендикулярною
до площини, якщо
вона перетинає цю
площину і перпендикулярна до
кожної прямої, яка
лежить у площині і
проходить через
точку перетину цих
прямих.

7. теорема:

a
Якщо одна з двох
a1
α
паралельних прямих
перпендикулярна до
площини, то і друга
пряма
перпендикулярна до
цієї площини.
Дві прямі, перпендикулярні до однієї
площини, - паралельні

8. Перпендикуляром, опущеним з даної точки на площину, називають відрізок прямої, перпендикулярної до площини, що міститься між

даною точкою і площиною.
a
АО – перпендикуляр,
A
B
O
до плану
α
опущений з даної
точки А на площину α
О – основа
перпендикуляра
АВ – похила,
проведена з точки А
на площину α
В – основа похилої
ОВ – проекція похилої
АВ на площину α

9. теорема про три перпендикуляри:

А
α
В
С
Пряма, проведена на
площині перпендикулярно до проекції
похилої, перпендикулярна і до цієї похилої.
І навпаки, якщо пряма
на площині перпендикулярна до похилої, то
вона перпендикулярна
і до проекції похилої.

10. Кут між прямою і площиною

Якщо пряма паралельна площині або
належить їй, то кут між ними дорівнює 0º.
а
а′
а
α
до плану
α

11.

С
α
В
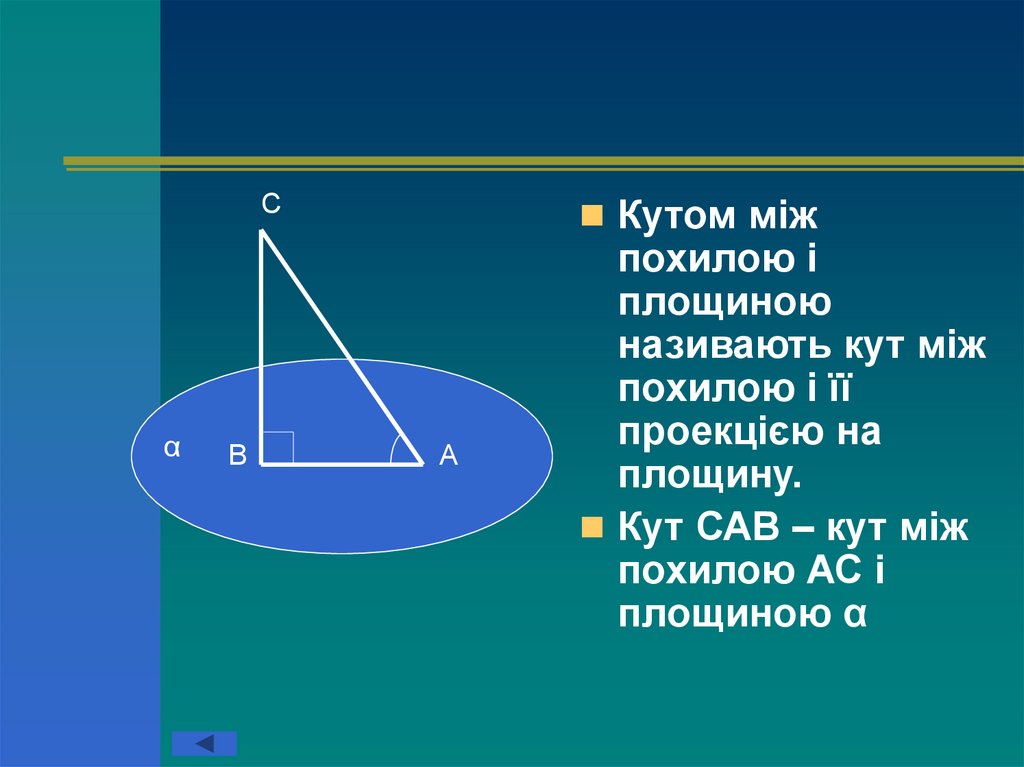
Кутом між
А
похилою і
площиною
називають кут між
похилою і її
проекцією на
площину.
Кут САВ – кут між
похилою АС і
площиною α

12. Перпендикулярні площини

Кутом між
β
α
М
a
c
до плану
b
площинами, які
перетираються,
називається кут
між прямими,
проведеними в цих
площинах
перпендикулярно
до лінії їх перетину.

13. Теорема: (ознака перпендикулярності площин)

Якщо одна з двох
β
c
α
b
а
площин проходить
через пряму,
перпендикулярну
до другої
площини, то такі
площини
перпендикулярні.

14.

Пряма, проведена
β
c
α
b
а
в одній з двох
перпендикулярних
площин
перпендикулярно
до прямої їх
перетину,
перпендикулярна
до другої площини.

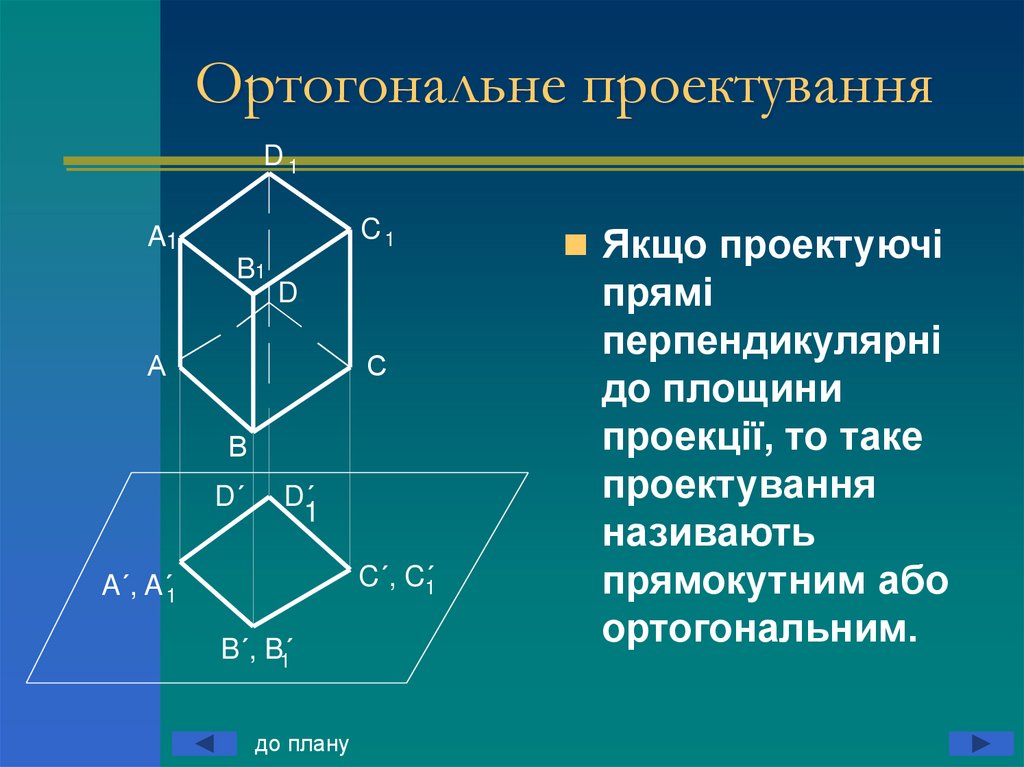
15. Ортогональне проектування

D1
C1
A1
B1
D
А
С
В
D´
D´
1
C´, C´1
A´, A´1
B´, B´1
до плану
Якщо проектуючі
прямі
перпендикулярні
до площини
проекції, то таке
проектування
називають
прямокутним або
ортогональним.

16.

Проекцією фігури на площину
називають множину проекцій усіх
точок даної фігури на дану площину.

17. Теорема:

α
Площа проекції
B
S
A
C
C1
γ
A1
S1
B1
β
многокутника
дорівнює площі
проектованого
многокутника,
помноженій на
косинус кута між їх
площинами.
S=S 1 cos γ

18. Самостійна робота

до плану

19. Завдання 1.

Доведіть, що пряма, перпендикулярна до
діагоналей паралелограма,
перпендикулярна і до його сторін.

20. Завдання 2.

ABCDA
1 B
1 C
1 D
1 - куб. Знайдіть кут між
прямими: а) BC 1 і СD; б) BC 1 і A D 1.

21. Завдання 3.

Знайдіть відстань між протилежними
ребрами куба, ребро якого дорівнює b.

22. Завдання 4.

Сторона рівностороннього трикутника
дорівнює 4 см. Знайдіть площу його
проекції на площину, яка з площиною
цього трикутника утворює кут 30°.

23. Тести

до плану

24. 1.Які прямі називають перпендикулярними?

а) що перетинаються;
б) кут між якими 90°;
в) кут між якими 45°;
г) що не перетинаються.

25. 2. Яку пряму називають перпендикулярною до площини?

а) яка перетинається з площиною;
б) яка при перетині з площиною утворює
кут 90° лише з однією прямою на цій
площині;
в) яка при перетині з площиною
перпендикулярна до кожної прямої, що
лежить на площині і проходить через
точку перетину цих прямих;
г) яка не перетинається з площиною.

26. 3. Дві прямі, перпендикулярні до однієї площини:

а) паралельні;
б) перпендикулярні;
в) мимобіжні;
г) перетинаються будь-як.

27. 4. Відрізком прямої, перпендикулярної до площини, що міститься між даною точкою і площиною, називають:

а) перпендикуляром до похилої;
б) похилою;
в) проекцією похилої на площину;
г) основою похилої.

28. 5. Якщо пряма паралельна площині або належить їй, то кут між ними дорівнює:

а) 45°;
б) 90°;
в) 180°;
г) 60°.

29. 6. Якщо одна з двох площин проходить через пряму, перпендикулярну до другої площини, то такі площини:

а) перетинаються;
б) утворюють кут 30°;
в) перпендикулярні;
г) паралельні.

30. Про автора:

Учитель математики
Решетилівського
ліцею імені
І.Л.ОЛійника
Мовчан Т. В.
2019р.